Übungsblatt 7

Reliabilität

  1. Wie ist die Reliabilität eines Items definiert?

    \(Rel(X_{i}) = \frac{Var(\tau_{i})}{Var(X_{i})}\)

  2. In welchem Wertebereich kann die Reliabilität eines Items liegen?

    Zwischen 0 und 1

  3. Ein Item i hat eine Reliabilität von \(Rel(X_{i}) = 0.5\). Interpretieren Sie diesen Wert.

    Der systematische Anteil an der Varianz dieses Items ist 50%. Oder: 50% der Varianz in der Itemantwort sind auf den wahren Wert zurückzuführen.

  4. Eine zufällig gezogene Person hat auf drei Items wie folgt geantwortet:

    Item 1: 3
    Item 2: 2
    Item 3: 4

    Bestimmen Sie die Realisationen der Zufallsvariablen \(\sum_{i=1}^{k} X_{i}\) und \(\bar{X}\)

    Die Realisation von \(\sum_{i=1}^{k} X_{i}\) ist \(\sum_{i=1}^{k} x_{i}\) = 3 + 2 + 4 = 9

    Die Realisation von \(\bar{X}\) ist \(\bar{x}\) = \(\frac{3 + 2 + 4}{3}\) = 3

  5. Wie ist die Reliabilität des Itemmittelwerts \(\bar{X}\) definiert?

    \(Rel(\bar{X}) = \frac{Var(\frac{1}{k}\sum_{i=1}^{k} \tau_{i})}{Var(\frac{1}{k}\sum_{i=1}^{k} X_{i})}\)

  6. Ihnen liegt eine Stichprobe von Personen vor, die auf drei Items geantwortet haben. Sie wissen, dass die drei Items einem essentiell parallelen Modell folgen. Zudem liegen Ihnen die empirischen Korrelationen der Items in der Stichprobe vor:

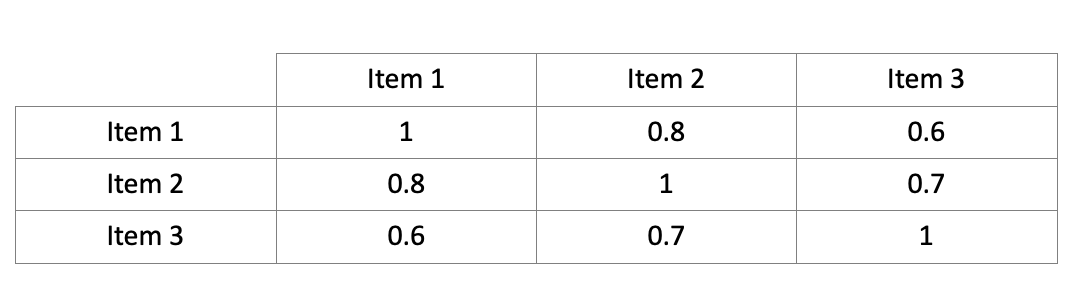
    1. Berechnen Sie die Schätzwerte für die Reliabilitäten der einzelnen Items

      Im essentiell parallelen Modell gilt \(Rel(X_{i}) = {Cor(X_{i}, X_{j})}\) für alle Items.

      Als Schätzwert für \(Cor(X_{i}, X_{j})\) verwenden wir den Mittelwert der empirischen Korrelationen aller Items:

      \(\frac{0.8 + 0.6 + 0.7}{3} = 0.7\)

      Also:

      Der Schätzwert für \(Rel(X_{1})\) ist \(rel(x_{1}) = 0.7\)
      Der Schätzwert für \(Rel(X_{2})\) ist \(rel(x_{2}) = 0.7\)
      Der Schätzwert für \(Rel(X_{3})\) ist \(rel(x_{3}) = 0.7\)

    2. Berechnen Sie den Schätzwert für die Reliabilität des Itemmittelwerts

      Im essentiell parallelen Modell gilt die vereinfachte Spearman-Brown-Formel:

      \(rel(\bar{x}) = \frac{k}{(k - 1) + \frac{1}{Rel(x_{i})}} = \frac{3}{(3 - 1) + \frac{1}{0.70}} \approx 0.88\)

  7. Ihnen liegt eine Stichprobe von Personen vor, die auf drei Items geantwortet haben. Sie wissen, dass die drei Items einem \(\tau\)-äquivalenten Modell folgen. Zudem liegen Ihnen die empirischen Varianzen und Kovarianzen der Items in der Stichprobe vor:

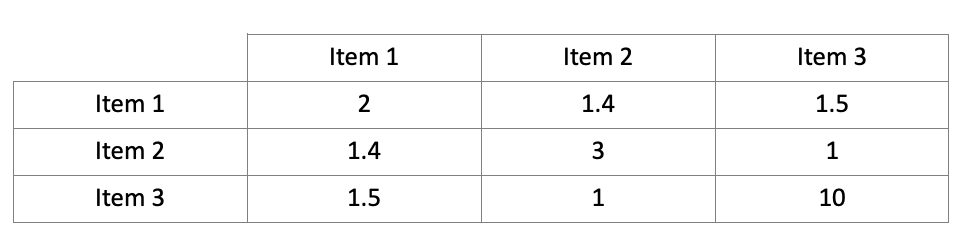
    1. Berechnen Sie die Schätzwerte für die Reliabilitäten der einzelnen Items

      Im \(\tau\)-äquivalenten Modell gilt \(Rel(X_{i}) = \frac{Cov(X_{i}, X_{j})}{Var(X_{i})}\) für alle Items

      Als Schätzwert für \(Cov(X_{i}, X_{j})\) verwenden wir den Mittelwert der empirischen Kovarianzen aller Items:

      \(\frac{1.4 + 1.5 + 1}{3} = 1.3\)

      Als Schätzwerte für die Varianzen \(Var(X_{i})\) der Items verwenden wir die empirischen Varianzen der Items:
      Der Schätzwert für \(Var(X_{1})\) ist \(var(x_{1}) = 2\)
      Der Schätzwert für \(Var(X_{2})\) ist \(var(x_{2}) = 3\)
      Der Schätzwert für \(Var(X_{3})\) ist \(var(x_{3}) = 10\)

      Also:

      Der Schätzwert für \(Rel(X_{1})\) ist \(rel(x_{1}) = \frac{1.3}{2} = 0.65\)
      Der Schätzwert für \(Rel(X_{2})\) ist \(rel(x_{2}) = \frac{1.3}{3} = 0.43\)
      Der Schätzwert für \(Rel(X_{3})\) ist \(rel(x_{3}) = \frac{1.3}{10} = 0.13\)

    2. Berechnen Sie den Schätzwert für die Reliabilität des Itemmittelwerts

      Im \(\tau\)-äquivalenten Modell gilt die Spearman-Brown-Formel:

      \(rel(\bar{x}) = \frac{k^{2}}{k(k - 1) + \sum_{i=1}^{k} \frac{1}{Rel(x_{i})}} = \frac{3^{2}}{3(3 - 1) + \frac{1}{0.65} + \frac{1}{0.43} + \frac{1}{0.13}} \approx 0.51\)

  8. Ihnen liegt eine Stichprobe von Personen vor, die auf vier Items geantwortet haben. Sie wissen, dass die vier Items einem \(\tau\)-kongenerischen Modell folgen. Zudem liegen Ihnen folgende R-Outputs vor:

    Schätzwerte für die Modellparameter:

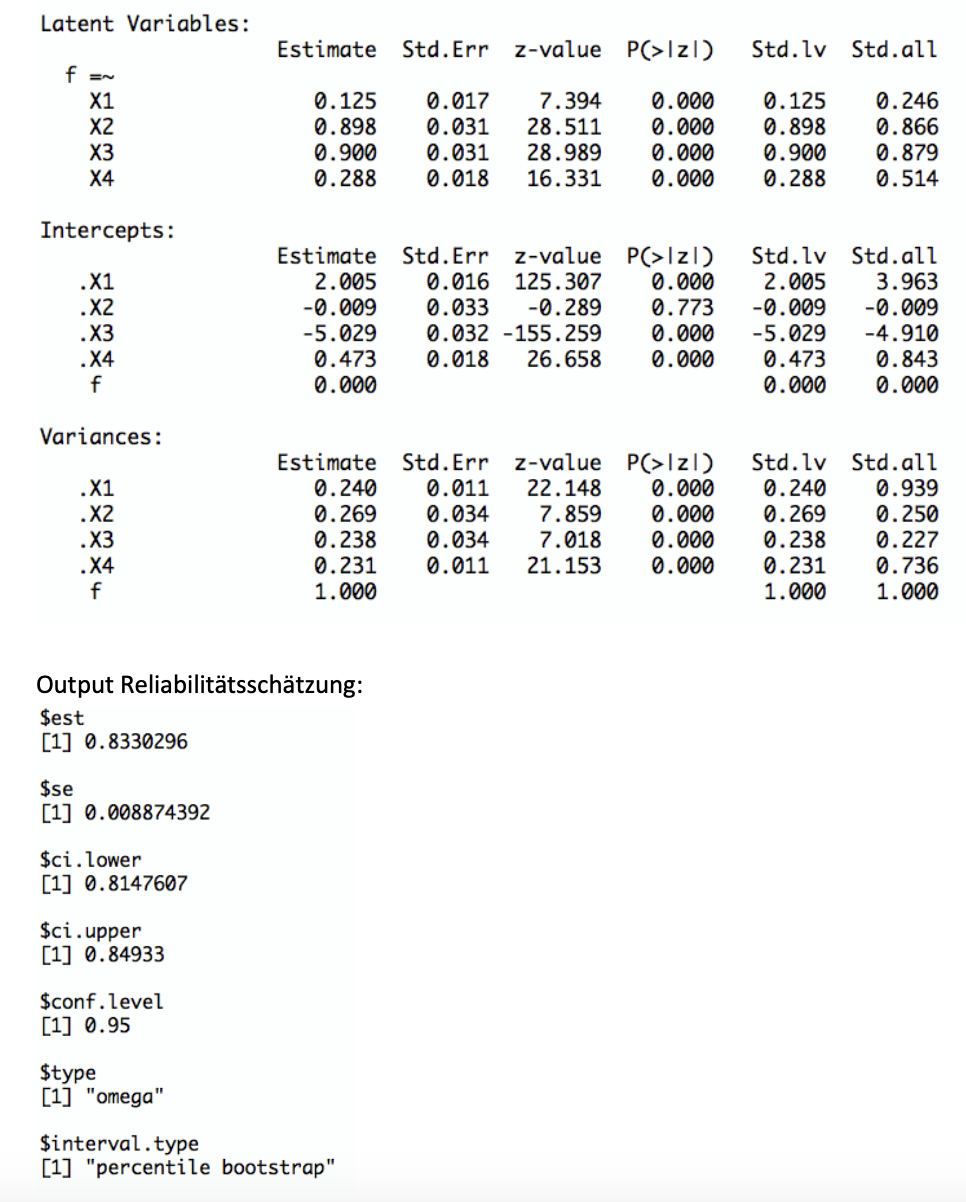
    1. Geben Sie die Schätzwerte für die Reliabilitäten der einzelnen Items an

      Im \(\tau\)-kongenerischen Modell gilt

      \(Rel(X_{i}) = \lambda_{zil}^{2}\)

      Aus dem Output mit den Parameterschätzungen ergibt sich:
      Der Schätzwert für \(\lambda_{z11}\) ist 0.246
      Der Schätzwert für \(\lambda_{z21}\) ist 0.866
      Der Schätzwert für \(\lambda_{z31}\) ist 0.879
      Der Schätzwert für \(\lambda_{z41}\) ist 0.514

      Und somit:
      Der Schätzwert für \(Rel(X_{1})\) ist \(rel(x_{1}) = 0.246^{2} = 0.06\)
      Der Schätzwert für \(Rel(X_{2})\) ist \(rel(x_{2}) = 0.866^{2} = 0.75\)
      Der Schätzwert für \(Rel(X_{3})\) ist \(rel(x_{3}) = 0.879^{2} = 0.77\)
      Der Schätzwert für \(Rel(X_{4})\) ist \(rel(x_{4}) = 0.514^{2} = 0.26\)

    2. Interpretieren Sie das Konfidenzintervall für die Reliabilität des Itemmittelwert

      Die plausiblen Werte für die Reliabilität des Itemmittelwerts liegen zwischen 0.81 und 0.85.

  9. In welchen Modellen entspricht Cronbach \(\alpha\) der Reliabilität des Itemmittelwerts?

    • Parallel
    • essentiell parallel
    • \(tau\)-äquivalent
    • essentiell \(tau\)-äquivalent

  10. Die Reliabilität welcher Größen wird jeweils geschätzt bei…

    1. der internen Konsistenz-Methode

      Die Reliabilität des Mittelwert aller Items des Tests

    2. der Split-Half-Methode

      Die Reliabilität des Mittelwert aller Items des Tests

    3. der Paralleltest-Methode

      Die Reliabilität des Testergebnisses beider parallelen Versionen des Tests

    4. der Retest-Methode

      Die Reliabilität des Testergebnisses des Tests

  11. Sie haben die Items Ihres psychologischen Tests in zwei Hälften geteilt und für jede Person in Ihrer Stichprobe jeweils den Mittelwert der Items dieser beiden Testhälften berechnet. Als empirische Korrelation zwischen den beiden Mittelwerten der Testhälften ergibt sich der Wert 0.7. Bestimmen Sie die Reliabilität des Tests mithilfe der Split-Half-Methode.

    Die Formel für die Reliabilität nach der Split-Half-Methode ist

    \(Rel(\bar{X}) = \frac{2 \cdot Cor(\bar{X}_{1}, \bar{X}_{2})}{Cor(\bar{X}_{1}, \bar{X}_{2}) + 1}\)

    Es ergibt sich ein Schätzwert von

    \(\frac{2 \cdot 0.7}{0.7 + 1} = 0.82\)