Übungsblatt 9

Einzelfalldiagnostik

  1. Was ist der Unterschied zwischen \(\theta\) und \(\theta_{Person}\)?

    \(\theta\) ist eine Zufallsvariable, \(\theta_{Person}\) ist eine (unbekannte) Konstante.
    \(\theta_{Person}\) ist der Wert einer festen Person auf der latenten Variable.
    \(\theta\) ist der Wert einer zufällig gezogenen Person auf der latenten Variable mit \(\theta_{Person}\) als Realisation.

  2. Was ist der Standardmessfehler bei der Schätzung von \(\theta_{Person}\) ?

    Die Standardabweichung der Schätzfunktion \(\hat{\theta}_{Person}\).

  3. Warum sollte in der Einzelfalldiagnostik für \(\theta_{Person}\) immer ein Konfidenzintervall statt einem einfachen (Punkt-)Schätzwert berechnet werden?

    Da der Punktschätzwert den Messfehler nicht berücksichtigt.

  4. Was versteht man unter einer Normstichprobe?

    Die Stichprobe von (zufällig gezogenen) Personen, an der die Skalierung des Tests vorgenommen wird und auf Basis derer die Modellparameter geschätzt werden.

  5. Eine Person hat auf vier parallelen Reaktionszeit-Items folgende Reaktionszeiten gezeigt:

    Item 1: 70
    Item 2: 50
    Item 3: 60
    Item 4: 50

    Ihnen liegen folgende Outputs aus der Normstichprobe vor:

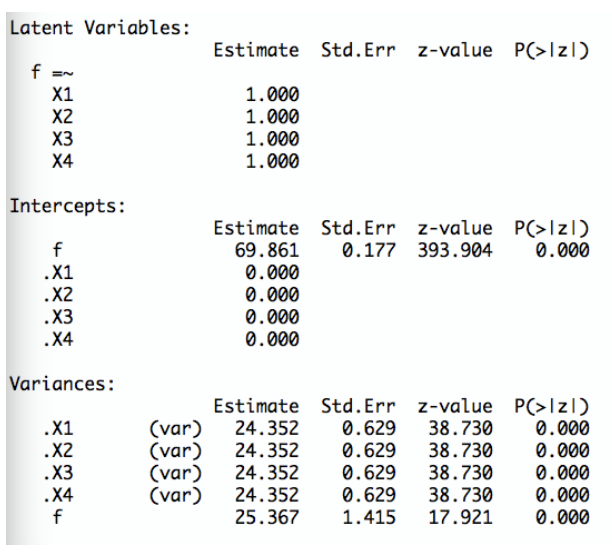
    1. Berechnen Sie den Schätzwert für den Standardmessfehler

      \(\hat{SE}(\hat{\theta}_{Person}) = \sqrt{\frac{Var(\epsilon_{i})}{k}} = \sqrt{\frac{24.352}{4}} \approx 2.47\)

    2. Berechnen Sie den Schätzwert für \(\theta_{Person}\)

      \(\hat{\theta}_{Person} = \frac{1}{k} \sum_{i=1}^{k} x_{iPerson} = \frac{70 + 50 + 60 + 50}{4} = 57.5\)

    3. Berechnen Sie ein 95%-Konfidenzintervall für \(\theta_{Person}\)

      \[\begin{align*} & I_{Person} \\ &= [\hat{\theta}_{Person} \pm z_{1-\frac{a}{2}} \cdot \hat{SE}(\hat{\theta}_{Person})] \\ &= [57.5 \pm 1.96 \cdot 2.47] \\ &= [52.66; 62.34] \end{align*}\]

    4. Geben Sie die Schätzwerte für \(E(\theta)\), \(Var(\theta)\) und \(\sqrt{Var(\theta)}\) an

      Der Schätzwert für \(E(\theta)\) ist 69.861
      Der Schätzwert für \(Var(\theta)\) ist 25.367
      Der Schätzwert für \(\sqrt{Var(\theta)}\) ist \(\sqrt{25.367} = 5.04\)

    5. Interpretieren Sie das Konfidenzintervall im normorientierten Sinne (unterdurchschnittlich, durchschnittlich, überdurchschnittlich etc.)

      Wir gehen davon aus, dass die Person einen unterdurchschnittlichen Wert auf der latenten Variable aufweist.
      Das gesamte Konfidenzintervall der Person liegt unter dem Wert 69.861 – 5.04 = 64.82, der eine Standardabweichung unter dem Populationsmittelwert liegt.

    Eine zweite Person hat auf den vier Items folgende Reaktionszeiten gezeigt:

    Item 1: 40
    Item 2: 60
    Item 3: 80
    Item 4: 90

    Sie wollen wissen, ob diese Person einen höheren latenten Variablenwert als die erste Person hat

    1. Stellen Sie die statistischen Hypothesen auf

      \(H_{0}: \theta_{Person2} \leq \theta_{Person1}\)
      \(H_{1}: \theta_{Person2} > \theta_{Person1}\)

    2. Berechnen Sie die Realisation der Teststatistik

      \[\begin{align*} & \hat{\theta}_{Person1} = 57.5 \\ & \hat{\theta}_{Person2} = \frac{1}{k} \sum_{i=1}^{k} x_{iPerson} = \frac{40 + 60 + 80 + 90}{4} = 67.5 \\ & z = \frac{\hat{\theta}_{Person2} - \hat{\theta}_{Person1}}{\sqrt{2} \cdot \hat{SE}(\hat{\theta}_{Person})} = \frac{67.5 - 57.5}{\sqrt{2} \cdot 2.47} = 2.86 \end{align*}\]

    3. Treffen Sie eine Testentscheidung

      Da \(z > z_{krit,rechts} = 1.64\), lehnen wir die \(H_{0}\) ab. Wir entscheiden uns dafür, dass Person 2 einen höheren latenten Variablenwert als Person 1 aufweist.

  6. Eine Person hat auf vier essentiell \(\tau\)-äquivalente Items wie folgt geantwortet:

    Item 1: 5 Item 2: 4 Item 3: 5 Item 4: 4

    Ihnen liegen folgende Outputs aus der Normstichprobe vor:

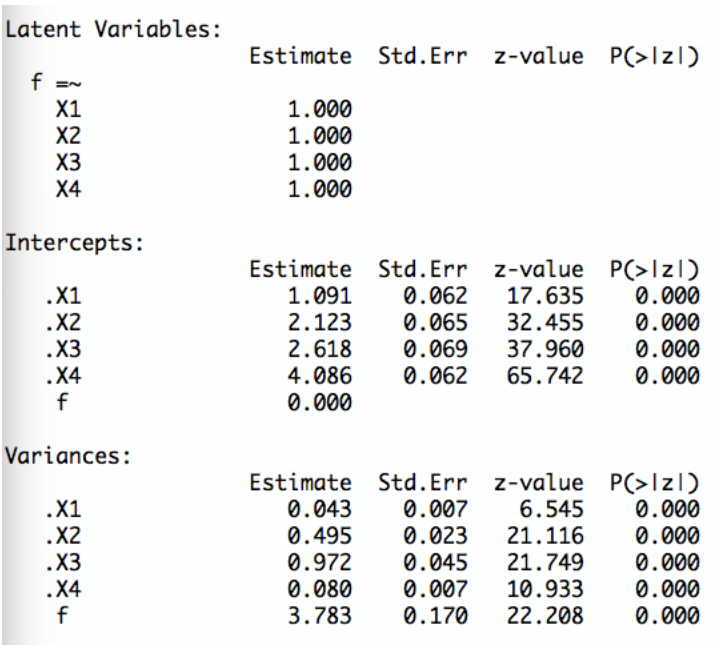
    1. Berechnen Sie ein 95%-Konfidenzintervall für \(\theta_{Person}\)

      \[\begin{align*} & \hat{SE}(\hat{\theta}_{Person}) = \frac{1}{\sqrt{\sum_{i=1}^{k} \frac{1}{var(\epsilon_{i})}}} = \frac{1}{\sqrt{\frac{1}{0.043} + \frac{1}{0.495} + \frac{1}{0.972} + \frac{1}{0.080}}} \approx 0.16 \\ \\ & \hat{\theta}_{Person} = \frac{\sum_{i=1}^{k} \frac{x_{iPerson} - \sigma_{i}}{var(\epsilon_{i})}}{\sum_{i=1}^{k} \frac{1}{var(\epsilon_{i})}} \\ \\ &= \frac{\frac{5 - 1.091}{0.043} + \frac{4 - 2.123}{0.495} + \frac{5 - 2.618}{0.972} + \frac{4 - 4.086}{0.080}}{\frac{1}{0.043} + \frac{1}{0.495} + \frac{1}{0.972} + \frac{1}{0.080}} \approx 2.48 \\ \\ & I_{Person} \\ &= [\hat{\theta}_{Person} \pm z_{1-\frac{a}{2}} \cdot \hat{SE}(\hat{\theta}_{Person})] \\ &= [2.48 \pm 1.96 \cdot 0.16] \\ &= [2.17; 2.79] \end{align*}\]

    2. Rechnen Sie die Grenzen des Konfidenzintervalls in IQ-Werte um

      \(E(\theta)\) ist aufgrund der Normierung gleich 0. Der Schätzwert für \(Var(\theta)\) ist 3.783 und somit der Schätzwert für \(\sqrt{Var(\theta)}\) gleich \(\sqrt{3.783} = 1.94\)

      Schritt 1: Umrechnen der Intervallgrenzen in z-standardisierte Werte nach der Formel

      \(\hat{\theta}_{Person, z-Wert} = \frac{\hat{\theta}_{Person} - E(\theta)}{\sqrt{Var(\theta)}}\)

      ergibt als untere Grenze \(\frac{2.17 - 0}{1.94} = 1.12\) und als obere Grenze \(\frac{2.79 - 0}{1.94} = 1.44\)

      Schritt 2: Umrechnen dieser Grenzen in IQ-Werte nach der Formel

      \(\hat{\theta}_{Person,Normwert} = E(\theta_{Norm}) + STD(\theta_{Norm}) \cdot \hat{\theta}_{Person, z-Wert}\)

      mit \(E(\theta_{Norm}) = 100\) und \(STD(\theta_{Norm}) = 15\) ergibt sich
      als untere Grenze \(100 + 15 \cdot 1.12 = 116.8\)
      und als obere Grenze \(100 + 15 \cdot 1.44 = 121.6\)

      Das Konfidenzintervall auf der Basis der IQ-Normwerte ist also \([116.8; 121.6]\)

    3. Interpretieren Sie das Konfidenzintervall im normorientierten Sinne

      Wir gehen davon aus, dass die Person einen überdurchschnittlichen Wert auf der latenten Variable aufweist.
      Das gesamte Konfidenzintervall der Person liegt über dem Wert 100 + 15 = 115, der eine Standardabweichung über dem Populationsmittelwert liegt.

  7. Eine Person hat auf vier \(\tau\)-kongenerische Items wie folgt geantwortet:

    Item 1: 3 Item 2: 1 Item 3: 3 Item 4: 2

    Ihnen liegen folgende Outputs aus der Normstichprobe vor:

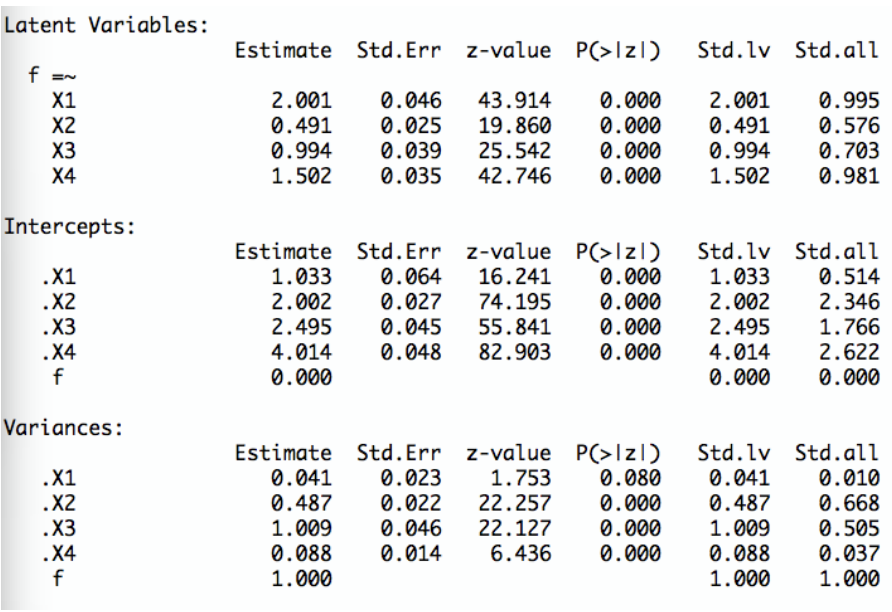
    1. Rechnen Sie die Itemantworten \(x_{iPerson}\) der Person in z-standardisierte Itemantworten \(z_{iPerson}\) um. Verwenden Sie dabei folgende Schätzwerte für die Varianzen der Items:

      \(var(X_{1}): 1\)
      \(var(X_{2}): 1.1\)
      \(var(X_{3}): 2\)
      \(var(X_{4}): 1.2\)

      Formel für die Umrechnung in z-standardisierte Itemantworten:

      \(Z_{iPerson} = \frac{X_{iPerson} - E(X_{i})}{\sqrt{Var(X_{i})}} = \frac{X_{iPerson} - \sigma_{i}}{\sqrt{Var(X_{i})}}\)

      Damit ergibt sich:

      \(z_{1Person} = \frac{3 - 1.033}{\sqrt{1}} = 1.97\)

      \(z_{2Person} = \frac{1 - 2.002}{\sqrt{1.1}} = -0.96\)

      \(z_{3Person} = \frac{3 - 2.495}{\sqrt{2}} = 0.36\)

      \(z_{4Person} = \frac{2 - 4.014}{\sqrt{1.2}} = -1.84\)

    2. Berechnen Sie ein 95%-Konfidenzintervall für \(\theta_{Person}\)

      \[\begin{align*} & \hat{SE}(\hat{\theta}_{Person}) = \frac{1}{\sqrt{\sum_{i=1}^{k} \frac{\beta^{2}_{zi}}{1-\beta^{2}_{zi}}}} = \frac{1}{\sqrt{\frac{0.995^{2}}{1 - 0.995^{2}} + \frac{0.576^{2}}{1 - 0.576^{2}} + \frac{0.703^{2}}{1 - 0.703^{2}} + \frac{0.981^{2}}{1 - 0.981^{2}}}} \approx 0.09 \\ \\ & \hat{\theta}_{Person} = \frac{\sum_{i=1}^{k} \frac{\beta_{zi} \cdot z_{iPerson}}{1 - \beta^{2}_{zi}}}{\sum_{i=1}^{k} \frac{\beta^{2}_{zi}}{1 - \beta^{2}_{zi}}} = \frac{\frac{0.995 \cdot 1.97}{1 - 0.995^{2}} + \frac{0.576 \cdot (-0.96)}{1 - 0.576^{2}} + \frac{0.703 \cdot 0.36}{1 - 0.703^{2}} + \frac{0.981 \cdot (-1.84)}{1 - 0.981^{2}}}{\frac{0.995^{2}}{1 - 0.995^{2}} + \frac{0.576^{2}}{1 - 0.576^{2}} + \frac{0.703^{2}}{1 - 0.703^{2}} + \frac{0.981^{2}}{1 - 0.981^{2}}} \approx 1.17 \\ \\ & I_{Person} = [\hat{\theta}_{Person} \pm z_{1-\frac{a}{2}} \cdot \hat{SE}(\hat{\theta}_{Person})] = [1.17 \pm 1.96 \cdot 0.09] = [0.99; 1.35] \end{align*}\]

    3. Rechnen Sie die Grenzen des Konfidenzintervalls in T-Werte um

      \(E(\theta)\) ist aufgrund der Normierung gleich 0. \(Var(\theta)\) ist aufgrund der Normierung gleich 1. Umrechnen der Intervallgrenzen in z-standardisierte Werte (Schritt 1) ist somit nicht notwendig.

      Schritt 2: Umrechnen der Intervallgrenzen in T-Werte nach der Formel

      \(\hat{\theta}_{Person,Normwert} = E(\theta_{Norm}) + STD(\theta_{Norm}) \cdot \hat{\theta}_{Person,z-Wert}\)

      mit \(E(\theta_{Norm}) = 50\) und \(STD(\theta_{Norm}) = 10\) ergibt
      als untere Grenze \(50 + 10 \cdot 0.99 = 59.9\) und
      als obere Grenze \(50 + 10 \cdot 1.35 = 63.5\)

      Das Konfidenzintervall auf der Basis der T-Normwerte ist also \([59.9; 63.5]\)

    4. Interpretieren Sie das Konfidenzintervall im normorientierten Sinne

      Wir gehen davon aus, dass die Person einen durchschnittlichen bis überdurchschnittlichen Wert auf der latenten Variable aufweist.
      Das Konfidenzintervall der Person überschneidet den Wert 50 + 10 = 60, der eine Standardabweichung über dem Populationsmittelwert liegt.