Übungsblatt 3

Testtheorie

  1. Nennen Sie die zwei Axiome der klassischen Testtheorie.

    Axiom 1: Für jedes Item i ist \(\tau_{i}\) die Zufallsvariable, deren Realisation der wahre Wert \(\tau_{iPerson}\) der Itemantwort der zufällig gezogenen Person ist

    Axiom 2: \(\epsilon_{i} = X_{i} - \tau_{i}\)

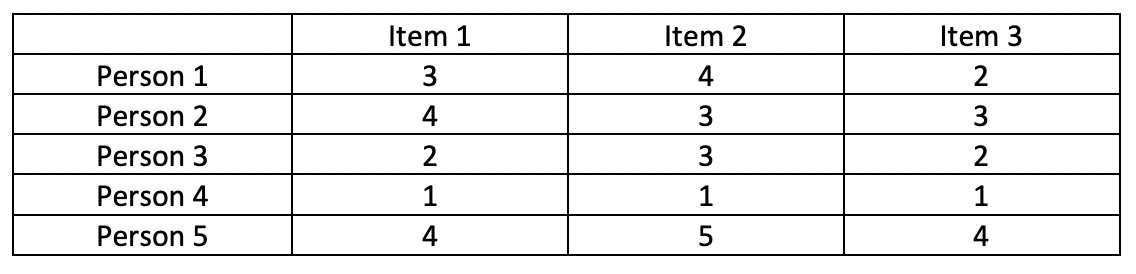
  2. Fünf zufällig gezogene Personen haben auf drei Items eines Tests geantwortet. Nehmen Sie an, die erste Person aus der Stichprobe hätte auf den drei Items die wahren Werte \(\tau_{1Person} = 2.7\), \(\tau_{2Person} = 3.5\) und \(\tau_{3Person} = 3\). In welchen Werten hätten sich dann die Fehlervariablen \(\epsilon_{1}\), \(\epsilon_{2}\) und \(\epsilon_{3}\) realisiert?

    In den Werten:
    \(3 – 2.7 = 0.3\),
    \(4 – 3.5 = 0.5\) und
    \(2 – 3 = -1\)

  3. Bonus: Beweisen Sie mithilfe der Axiome und Folgerungen aus den Vorlesungsfolien die folgende weitere Folgerung:

    \(Cov(X_{i}, \epsilon_{i}) = Var(\epsilon_{i})\)

    Was bedeutet diese Folgerung?

    Hinweis: Sie benötigen Folgerung E1, Kovarianzrechenregeln C7, C3 und Folgerung E4.

    \(Cov(X_{i}, \epsilon_{i}) = Cov(\epsilon_{i} + \tau_{i}, \epsilon_{i}) = Cov(\epsilon_{i}, \epsilon_{i}) + Cov(\tau_{i}, \epsilon_{i}) = Var(\epsilon_{i}) + 0 = Var(\epsilon_{i})\)

    Die Kovarianz der Itemantwort der zufälligen Person auf Item i mit der Fehlervariable auf Item i entspricht der Varianz der Fehlervariable auf Item i

  4. Was ist der Unterschied zwischen \(\theta\) und \(\theta_{Person}\)? Wie hängen diese beiden Größen zusammen?

    \(\theta\) ist eine Zufallsvariable, \(\theta_{Person}\) ist eine (unbekannte) Konstante.
    \(\theta_{Person}\) ist der Wert einer festen Person auf der latenten Variable.
    \(\theta_{Person}\) ist die Realisation der Zufallsvariable \(\theta\), falls eine Person zufällig gezogen wird.

  5. Ordnen Sie die folgenden Größen jeweils ihrer Interpretation zu:

    \(E(X_{iPerson})\)
    \(Var(X_{iPerson})\)
    \(E(X_{i})\)
    \(Var(X_{i})\)
    \(E(\tau_{i})\)
    \(Var(\tau_{i})\)
    \(E(\theta)\)
    \(Var(\theta)\)

    Mittelwert der latenten Variable in der Population
    Wahrer Wert einer Person auf Item i
    Mittelwert der Itemantworten auf Item i von unendlich vielen zufällig gezogenen Personen
    Mittelwert der wahren Werte auf Item i in der Population
    Varianz der Itemantworten auf Item i von unendlich vielen zufällig gezogenen Personen
    Varianz der wahren Werte auf Item i in der Population
    Varianz der Antworten einer festen Person auf Item i
    Varianz der latenten Variable in der Population

    \(E(X_{iPerson})\): Wahrer Wert einer Person auf Item i
    \(Var(X_{iPerson})\): Varianz der Antworten einer festen Person auf Item i
    \(E(X_{i})\): Mittelwert der Itemantworten auf Item i von unendlich vielen zufällig gezogenen Personen
    \(Var(X_{i})\): Varianz der Itemantworten auf Item i von unendlich vielen zufällig gezogenen Personen
    \(E(\tau_{i})\): Mittelwert der wahren Werte auf Item i in der Population
    \(Var(\tau_{i})\): Varianz der wahren Werte auf Item i in der Population
    \(E(\theta)\): Mittelwert der latenten Variable in der Population
    \(Var(\theta)\): Varianz der latenten Variable in der Population

  6. Nennen Sie die Annahmen des parallelen Modells

    \(\tau_{i} = \theta\) und somit \(X_{i} = \theta + \epsilon_{i}\) für alle Items i
    \(Var(\epsilon_{i}) = Var(\epsilon_{j})\) für alle Itempaare i,j
    \(Cov(\epsilon_{i}, \epsilon_{j}) = 0\) für alle Itempaare i,j

  7. Wir betrachten einen Test mit den folgenden drei Items:

    Wir nehmen an, dass für diese drei Items das parallele Modell gilt

    1. Um welche psychologische Variable könnte es sich hier bei \(\theta_{Person}\) handeln?

    Depression

    1. Angenommen, wir ziehen eine Person zufällig und diese hat einen Wert auf der latenten Variable von \(\theta_{Person} = 3.4\). Was bedeutet dieser Wert?

    Die gezogene Person hat einen Depressionswert von 3.4

    1. Welche wahren Werte hätte diese Person auf den drei Items?

    3.4 auf allen drei Items, da im parallelen Modell \(\tau_{i} = \theta\) und deshalb auch \(\tau_{iPerson} = \theta_{Person}\) für alle Items gilt

    1. Angenommen, die Person kreuzt auf den drei Items tatsächlich die Werte 3, 4 und 3 an. In welchen Werten hätten sich in diesem Fall die Zufallsvariablen \(X_{2}\), \(\tau_{2}\), \(\epsilon_{2}\) und \(\theta\) realisiert?

    \(X_{2}\) hätte sich in dem Wert \(x_{2} = 4\) realisiert
    \(\tau_{2}\) hätte sich in dem Wert \(\tau_{2Person} = 3.4\) realisiert
    \(\epsilon_{2}\) hätte sich in dem Wert \(x_{2} - \tau_{2Person} = 4 − 3.4 = 0.6\) realisiert
    \(\theta\) hätte sich in dem Wert \(\theta_{Person} = 3.4\) realisiert

    1. Erläutern Sie alle Annahmen des parallelen Modells am Beispiel dieser drei Items

    Erste Annahme: Die durchschnittlichen Antworten einer Person auf die drei Items bei unendlich Wiederholung des Tests sind exakt gleich und entsprechen der Ausprägung der Person auf der latenten Variable Depression

    Zweite Annahme: Die empirischen Varianzen der Abweichungen zwischen den durchschnittlichen Itemantworten einer Person und den tatsächlichen Itemantworten bei unendlicher Wiederholung des Tests sind für die drei Items gleich

    Dritte Annahme: Die empirischen Kovarianzen der Abweichungen der tatsächlichen Itemantworten von den durchschnittlichen Itemantworten einer Person bei unendlicher Wiederholung des Tests sind für alle Itempaare Null