Übungsblatt 4

Testtheorie

1. Nennen Sie jeweils die Annahmen der folgenden testtheoretischen Modelle

   1. Paralleles Modell

      TippLösung

      \(\tau_{i} = \theta\) und somit \(X_{i} = \theta + \epsilon_{i}\) für alle Items i

      \(Var(\epsilon_{i}) = Var(\epsilon_{j})\) für alle Itempaare i,j

      \(Cov(\epsilon_{i}, \epsilon_{j}) = 0\) für alle Itempaare i,j

   2. Essentiell paralleles Modell

      TippLösung

      \(\tau_{i} = \sigma_{i} + \theta\) und somit \(X_{i} = \sigma_{i} + \theta + \epsilon_{i}\) für alle Items i

      \(Var(\epsilon_{i}) = Var(\epsilon_{j})\) für alle Itempaare i,j

      \(Cov(\epsilon_{i}, \epsilon_{j}) = 0\) für alle Itempaare i,j

   3. \(\tau\)-äquivalentes Modell

      TippLösung

      \(\tau_{i} = \theta\) und somit \(X_{i} = \theta + \epsilon_{i}\) für alle Items i

      \(Cov(\epsilon_{i}, \epsilon_{j}) = 0\) für alle Itempaare i,j

   4. Essentiell \(\tau\)-äquivalentes Modell

      TippLösung

      \(\tau_{i} = \sigma_{i} + \theta\) und somit \(X_{i} = \sigma_{i} + \theta + \epsilon_{i}\) für alle Items i

      \(Cov(\epsilon_{i}, \epsilon_{j}) = 0\) für alle Itempaare i,j

   5. \(\tau\)-kongenerisches Modell

      TippLösung

      \(\tau_{i} = \sigma_{i} + \beta_{i} \cdot \theta\) und somit \(X_{i} = \sigma_{i} + \beta_{i} \cdot \theta + \epsilon_{i}\) für alle Items i

      \(Cov(\epsilon_{i}, \epsilon_{j}) = 0\) für alle Itempaare i,j

   6. Mehrdimensionales \(\tau\)-kongenerisches Modell

      TippLösung

      \(\tau_{i} = \sigma_{i} + \beta_{i1} \cdot \theta_{1} + \beta_{i2} \cdot \theta_{2} + ... + \beta_{iq} \cdot \theta_{q}\) und somit \(X_{i} = \sigma_{i} + \beta_{i1} \cdot \theta_{1} + \beta_{i2} \cdot \theta_{2} + ... + \beta_{iq} \cdot \theta_{q} + \epsilon_{i}\) für alle Items i

      \(Cov(\epsilon_{i}, \epsilon_{j}) = 0\) für alle Itempaare i,j

2. In welchen Annahmen unterscheiden sich

   1. das parallele und das essentiell parallele Modell?

      TippLösung

      In der ersten Annahme

      parallel: \(\tau_{i} = \theta\) für alle Items i
      essentiell parallel: \(\tau_{i} = \sigma_{i} + \theta\) für alle Items i

   2. das parallele und das \(\tau\)-äquivalente Modell?

      TippLösung

      In der Annahme bezüglich der Fehlervarianz

      parallel: \(Var(\epsilon_{i}) = Var(\epsilon_{j})\) für alle Itempaare i,j
      \(\tau\)-äquivalent: keine Annahme bezüglich der Gleichheit der Fehlervarianzen

   3. das parallele und das essentiell \(\tau\)-äquivalente Modell?

      TippLösung

      In der ersten Annahme und der Annahme bezüglich der Fehlervarianzen

      parallel: \(\tau_{i} = \theta\) für alle Items i und \(Var(\epsilon_{i}) = Var(\epsilon_{j})\) für alle Itempaare i,j
      essentiell \(\tau\)-äquivalent: \(\tau_{i} = \sigma_{i} + \theta\) für alle Items i und keine Annahme bezüglich der Gleichheit der Fehlervarianzen

   4. das parallele und das \(\tau\)-kongenerische Modell?

      TippLösung

      In der ersten Annahme und der Annahme bezüglich der Fehlervarianzen

      parallel: \(\tau_{i} = \theta\) für alle Items i und \(Var(\epsilon_{i}) = Var(\epsilon_{j})\) für alle Itempaare i,j
      \(\tau\)-kongenerisch: \(\tau_{i} = \sigma_{i} + \beta_{i} \cdot \theta\) für alle Items i und keine Annahme bezüglich der Gleichheit der Fehlervarianzen

   5. das essentiell parallele und das \(\tau\)-äquivalente Modell?

      TippLösung

      In der ersten Annahme und der Annahme bezüglich der Fehlervarianzen

      essentiell parallel: \(\tau_{i} = \sigma_{i} + \theta\) für alle Items i und \(Var(\epsilon_{i}) = Var(\epsilon_{j})\) für alle Itempaare i,j
      \(\tau\)-äquivalent: \(\tau_{i} = \theta\) für alle Items i und keine Annahme bezüglich der Gleichheit der Fehlervarianzen

   6. das \(\tau\)-äquivalente und das essentiell \(\tau\)-äquivalente Modell?

      TippLösung

      In der ersten Annahme

      \(\tau\)-äquivalent: \(\tau_{i} = \theta\) für alle Items i
      essentiell \(\tau\)-äquivalent: \(\tau_{i} = \sigma_{i} + \theta\) für alle Items i

   7. das \(\tau\)-äquivalente und das \(\tau\)-kongenerische Modell?

      TippLösung

      In der ersten Annahme

      \(\tau\)-äquivalent: \(\tau_{i} = \theta\) für alle Items i
      \(\tau\)-kongenerisch: \(\tau_{i} = \sigma_{i} + \beta_{i} \cdot \theta\) für alle Items i

   8. das essentiell \(\tau\)-äquivalente und das mehrdimensionale \(\tau\)-kongenerische Modell?

      TippLösung

      In der ersten Annahme

      essentiell \(\tau\)-äquivalent: \(\tau_{i} = \sigma_{i} + \theta\) für alle Items i
      mehrdimensional \(\tau\)-kongenerische: \(\tau_{i} = \sigma_{i} + \beta_{i1} \cdot \theta_{1} + \beta_{i2} \cdot \theta_{2} + ... + \beta_{iq} \cdot \theta_{q}\) für alle Items i

3. In welchen Modellen wird angenommen

   1. dass es Itemparameter gibt?

      TippLösung

      • essentiell parallel
      • essentiell \(\tau\)-äquivalent
      • \(\tau\)-kongenerisch
      • mehrdimensional \(\tau\)-kongenerisch

   2. dass die Varianzen der Fehlervariablen gleich sind?

      TippLösung

      • parallel
      • essentiell parallel

   3. dass es Steigungsparameter gibt?

      TippLösung

      • \(\tau\)-kongenerisch
      • mehrdimensional \(\tau\)-kongenerisch

   4. dass die Kovarianz der Fehlervariablen gleich 0 ist?

      TippLösung

      • parallel
      • essentiell parallel
      • \(\tau\)-äquivalent
      • essentiell \(\tau\)-äquivalent
      • \(\tau\)-kongenerisch
      • mehrdimensional \(\tau\)-kongenerisch

   5. dass mehr als eine latente Variable hinter den Itemantworten steht?

      TippLösung

      • mehrdimensional \(\tau\)-kongenerisch

4. Erläutern Sie, was die Annahme \(Var(\epsilon_{i}) = Var(\epsilon_{j})\) inhaltlich bedeutet.

   TippLösung

   Die Varianzen der Fehlervariablen sind für alle Items gleich groß

5. Erläutern Sie, was die Annahme \(Cov(\epsilon_{i}, \epsilon_{j}) = 0\) inhaltlich bedeutet.

   TippLösung

   Die Fehlervariablen zweier beliebiger Items des Tests kovariieren nicht

6. Wie kann der Itemparameter interpretiert werden?

   TippLösung

   Der Itemparameter eines Items i entspricht (in allen Modellen, in denen er vorkommt) dem Erwartungswert der Itemantwort einer zufällig gezogenen Person auf Item i (unter der Normierung \(E(\theta) = 0\))

7. Wie können die Steigungsparameter im \(\tau\)-kongenerischen Modell interpretiert werden?

   TippLösung

   Falls sich die latente Variable um eine Einheit erhöht, erhöht sich die durchschnittliche Itemantwort um \(\beta_{i}\) Einheiten

8. Wie können die Steigungsparameter im mehrdimensionalen \(\tau\)-kongenerischen Modell interpretiert werden?

   TippLösung

   Falls sich die latente Variable \(l\) um eine Einheit erhöht, erhöht sich die durchschnittliche Itemantwort auf Item i um \(\beta_{il}\) Einheiten, falls alle anderen latenten Variablen des Modells konstant bleiben

9. Geben Sie für alle Modelle an, welche Normierungsbedingungen jeweils getroffen werden müssen

   TippLösung

   parallel: keine
   essentiell parallel: \(E(\theta) = 0\)
   \(\tau\)-äquivalent: keine
   essentiell \(\tau\)-äquivalent: \(E(\theta) = 0\)
   \(\tau\)-kongenerisch: \(E(\theta) = 0\) und \(Var(\theta) = 1\)
   mehrdimensional \(\tau\)-kongenerisch: \(E(\theta_{l}) = 0\), \(Var(\theta_{l})\) = 1 und \(Cov(\theta_{l}, \theta_{m}) = 0\)

10. Zeigen Sie, dass im mehrdimensionalen \(\tau\)-kongenerischen Modell die Itemparameter den Erwartungswerten der Items entsprechen, also dass \(E(X_{i}) = \sigma_{i}\) für alle Items i.

    TippLösung

    \[\begin{align*} E(X_{i}) &= E(\sigma_{i} + \beta_{i1} \cdot \theta_{1} + \beta_{i2} \cdot \theta_{2} + ... + \beta_{iq} \cdot \theta_{q} + \epsilon_{i}) \\ &= E(\sigma_{i}) + E(\beta_{i1} \cdot \theta_{1}) + E(\beta_{i2} \cdot \theta_{2}) + ... + E(\beta_{iq} \cdot \theta_{q}) + E(\epsilon_{i}) \\ &= \sigma_{i} + 0 + 0 + ... + 0 + 0 \\ &= \sigma_{i} \end{align*}\]

11. Wir betrachten einen Test mit den folgenden drei Items:

    

    Wir nehmen an, dass für diese drei Items das zwei-dimensionale \(\tau\)-kongenerische Modell mit den latenten Variablen Depression \(\theta_{1}\) und Ermüdungsanfälligkeit \(\theta_{2}\) gilt.

    Ihnen sind folgende Größen bekannt:

    \(E(X_{1}) = 2.2\), \(E(X_{2}) = 3.5\), \(E(X_{3}) = 1.4\),
    \(Var(X_{1}) = 1\), \(Var(X_{2}) = 2\), \(Var(X_{3}) = 1\)

    Zudem kennen Sie die Steigungsparameter:

    \(\beta_{11} = 1 \quad \quad \beta_{12} = 0\)
    \(\beta_{21} = 2 \quad \quad \beta_{22} = 0\)
    \(\beta_{31} = 0 \quad \quad \beta_{32} = 1.5\)
    

    1. Skizzieren Sie das Modell in der Art von Folie 19 und 20 des dritten Foliensatzes zu den Modellen.

       TippLösung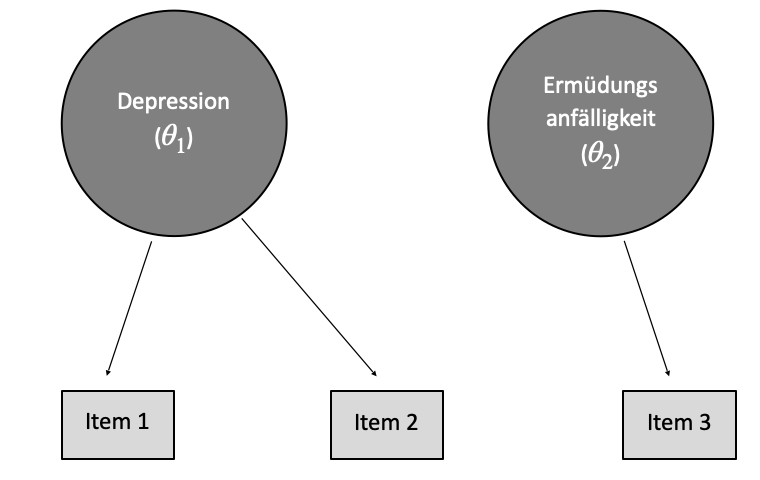

       

    2. Bestimmen Sie den Schwierigkeitsparameter für jedes Item.

       TippLösung

       \(\sigma_{1} = E(X_{1}) = 2.2\)
       \(\sigma_{2} = E(X_{2}) = 3.5\)
       \(\sigma_{3} = E(X_{3}) = 1.4\)

    3. Interpretieren Sie den Steigungsparameter der zweiten latenten Variable für das dritte Item.

       TippLösung

       Falls sich die Ermüdungsanfälligkeit um eine Einheit erhöht, erhöht sich die durchschnittliche Itemantwort auf Item 3 um \(\beta_{32} = 1.5\) Einheiten, (falls die Depression konstant bleibt) -> Die Aussage in Klammern muss in diesem Spezialfall nicht zwingend sein, da die Formel
       \(X_{3} = \beta_{31} \cdot \theta_{31} + \beta_{32} \cdot \theta_{32} + \epsilon_{3}\) sich durch \(\beta_{31} = 0\) von \(X_{3} = 0 \cdot \theta_{31} + \beta_{32} \cdot \theta_{32} + \epsilon_{3}\) auf \(X_{3} = \beta_{32} \cdot \theta_{32} + \beta_{31} + \epsilon_{3}\) reduziert.

    4. Interpretieren Sie den Steigungsparameter der zweiten latenten Variable für das erste Item.

       TippLösung

       Falls sich die Ermüdungsanfälligkeit um eine Einheit erhöht, erhöht sich die durchschnittliche Itemantwort auf Item 1 um \(\beta_{12} = 0\) Einheiten, falls die Depression konstant bleibt

    5. Bestimmen Sie für alle Items alle z-standardisierten Steigungsparameter \(\beta_{zil}\)

       TippLösung

       \(\beta_{z11} = \frac{\beta_{11}}{\sqrt{Var(X_{1})}} = \frac{1}{\sqrt{1}} = 1\)

       \(\beta_{z12} = \frac{\beta_{12}}{\sqrt{Var(X_{1})}} = \frac{0}{\sqrt{1}} = 0\)

       \(\beta_{z21} = \frac{\beta_{21}}{\sqrt{Var(X_{2})}} = \frac{2}{\sqrt{2}} = 1.41\)

       \(\beta_{z22} = \frac{\beta_{22}}{\sqrt{Var(X_{2})}} = \frac{2}{\sqrt{2}} = 0\)

       \(\beta_{z31} = \frac{\beta_{31}}{\sqrt{Var(X_{3})}} = \frac{0}{\sqrt{1}} = 0\)

       \(\beta_{z32} = \frac{\beta_{32}}{\sqrt{Var(X_{3})}} = \frac{1.5}{\sqrt{1}} = 1.5\)

12. Erläutern Sie, inwiefern das \(\tau\)-äquivalente Modell ein Spezialfall des \(\tau\)-kongenerischen Modells ist.

    TippLösung

    Das \(\tau\)-äquivalente und das \(\tau\)-kongenerische Modell unterscheiden sich nur in der ersten Annahme.
    \(\tau\)-äquivalent: \(\tau_{i} = \theta\) für alle Items i
    \(\tau\)-kongenerisch: \(\tau_{i} = \sigma_{i} + \beta_{i} \cdot \theta\) für alle Items i
    Falls im \(\tau\)-kongenerischen Modell für alle Items i \(\sigma_{i} = 0\) und \(\beta_{i} = 1\) gilt, ergibt sich \(\tau_{i} = 0 + 1 \cdot \theta = \theta\) für alle Items i und somit ein \(\tau\)-äquivalentes Modell

13. In der folgenden Grafik bedeutet ein Pfeil, dass das Modell in dem jeweiligen Kasten ein Spezialfall des darüberstehenden Modells ist. Tragen Sie die Modelle in die Kästen ein:

    

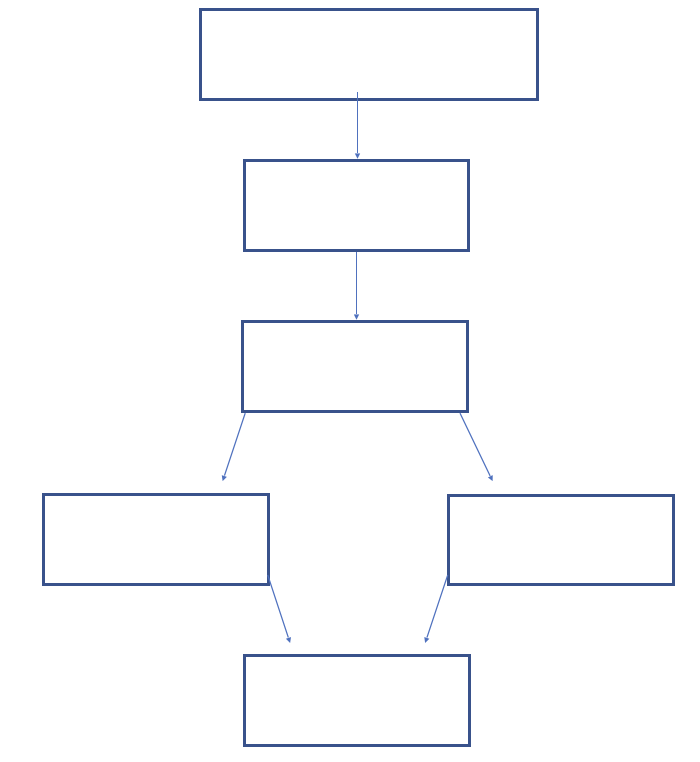    TippLösung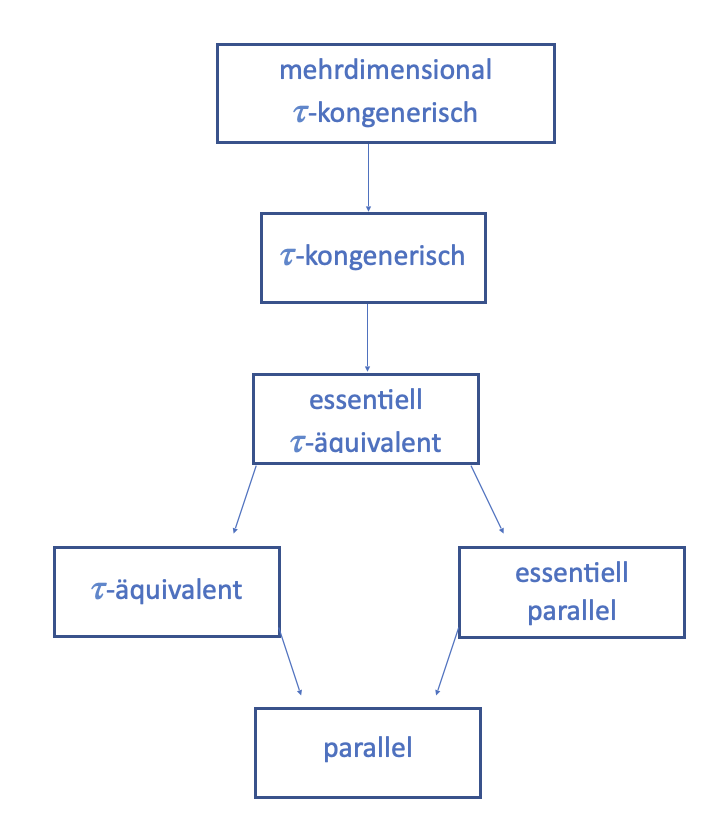

    

14. Erläutern Sie, was man unter Personenhomogenität versteht und nennen Sie ein Beispiel für eine Verletzung dieser Annahme in der Praxis.

    TippLösung

    Personenhomogenität bedeutet, dass für alle untersuchten Personen das gleiche testtheoretische Modell gilt.
    Beispiel für eine Verletzung der Personenhomogenität: für einen Teil der Population hängt ein Item negativ mit der latenten Variable zusammen (d.h. negativer Steigungsparameter im \(\tau\)-kongenerischen Modell) und für einen anderen Teil positiv (d.h. positiver Steigungsparameter im \(\tau\)-kongenerischen Modell)