Übungsblatt 5

Testtheorie

  1. Was versteht man unter dem Gütekriterium der Skalierung?

    Ein psychologischer Test gilt als skalierbar, wenn die Zuordnung der Messwerte zu den Personen auf der Basis eines empirisch nachgewiesenen testtheoretischen Modells geschieht.

  2. Warum ist die Skalierung ein zentrales Gütekriterium eines psychologischen Tests?

    Da das komplette weitere Vorgehen (Schätzung der Reliabilität, Schätzung der Modellparameter, Einzelfalldiagnostik) davon abhängt, welches testtheoretische Modell gilt.

  3. Was hat die Skalierung mit den Annahmen der testtheoretischen Modelle zu tun?

    Der empirische Nachweis eines testtheoretischen Modells geschieht durch Überprüfung der Folgerungen aus dessen Annahmen.

  4. Beschreiben Sie das allgemeine Prinzip bei der Überprüfung der Annahmen der testtheoretischen Modelle.

    Aus den Annahmen der testtheoretischen Modelle werden jeweils Folgerungen in Bezug auf beobachtbare Größen abgeleitet, die erfüllt sein müssen, falls die Annahmen gelten. Diese Folgerungen sind dann statistische Hypothesen, die wir mithilfe von Stichproben und statistischen Hypothesentests überprüfen.

  5. Geben Sie für alle in der Vorlesung besprochenen Modelle alle Folgerungen aus den Modellannahmen bezüglich \(E(X_{i})\), \(Var(X_{i})\) und \(Cov(X_{i}, X_{j})\) an.

    paralleles Modell:
    \(E(X_{i}) = E(X_{j})\) für alle Items i, j
    \(Var(X_{i}) = Var(X_{j})\) für alle Items i, j
    \(Cov(X_{i}, X_{j}) = Cov(X_{o}, X_{u})\) für alle Itempaare i, j und o, u

    essentiell paralleles Modell:
    \(Var(X_{i}) = Var(X_{j})\) für alle Items i, j
    \(Cov(X_{i}, X_{j}) = Cov(X_{o}, X_{u})\) für alle Itempaare i, j und o, u

    \(\tau\)-äquivalentes Modell:
    \(E(X_{i}) = E(X_{j})\) für alle Items i, j
    \(Cov(X_{i}, X_{j}) = Cov(X_{o}, X_{u})\) für alle Itempaare i, j und o, u

    essentiell \(\tau\)-äquivalentes Modell:
    \(Cov(X_{i}, X_{j}) = Cov(X_{o}, X_{u})\) für alle Itempaare i, j und o, u

    \(\tau\)-kongenerisches Modell:
    \(Cov(X_{i}, X_{j}) = \beta_{i} \cdot \beta_{j}\) für alle Itempaare i, j

    mehrdimensionales \(\tau\)-kongenerisches Modell:
    \(Cov(X_{i}, X_{j}) = \sum_{l=1}^{q} \beta_{il} \cdot \beta_{jl}\) für alle Itempaare i, j

  6. Sie haben einen psychologischen Test entworfen und wollen überprüfen, welchem testtheoretischen Modell dessen Items folgen. Sie erhalten folgende Outputs:

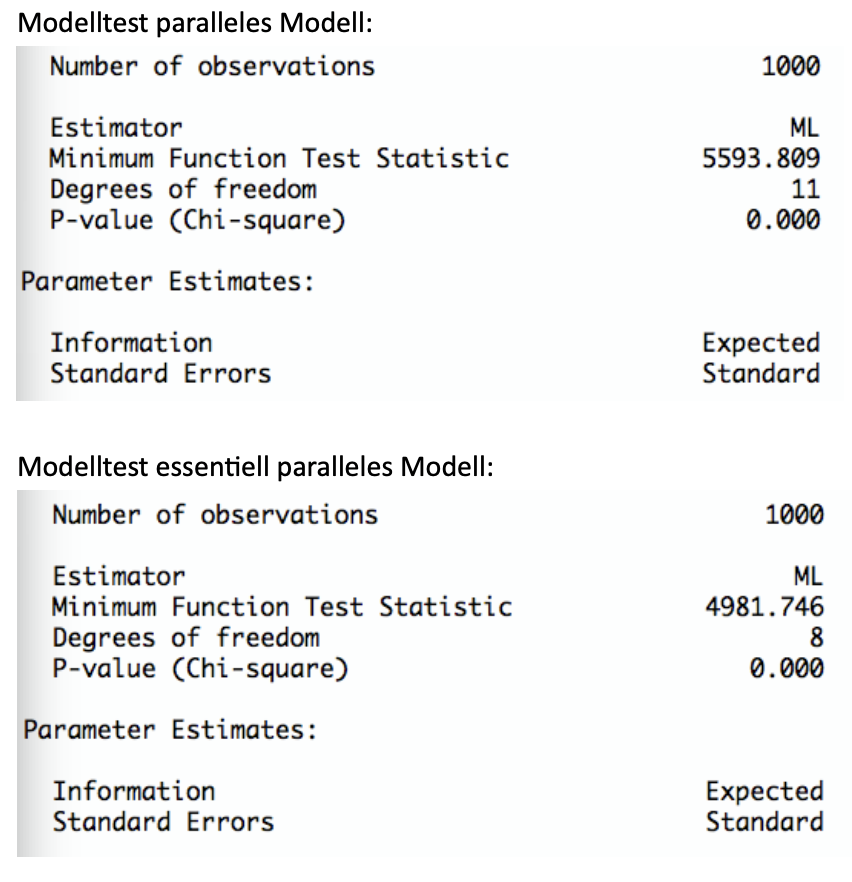
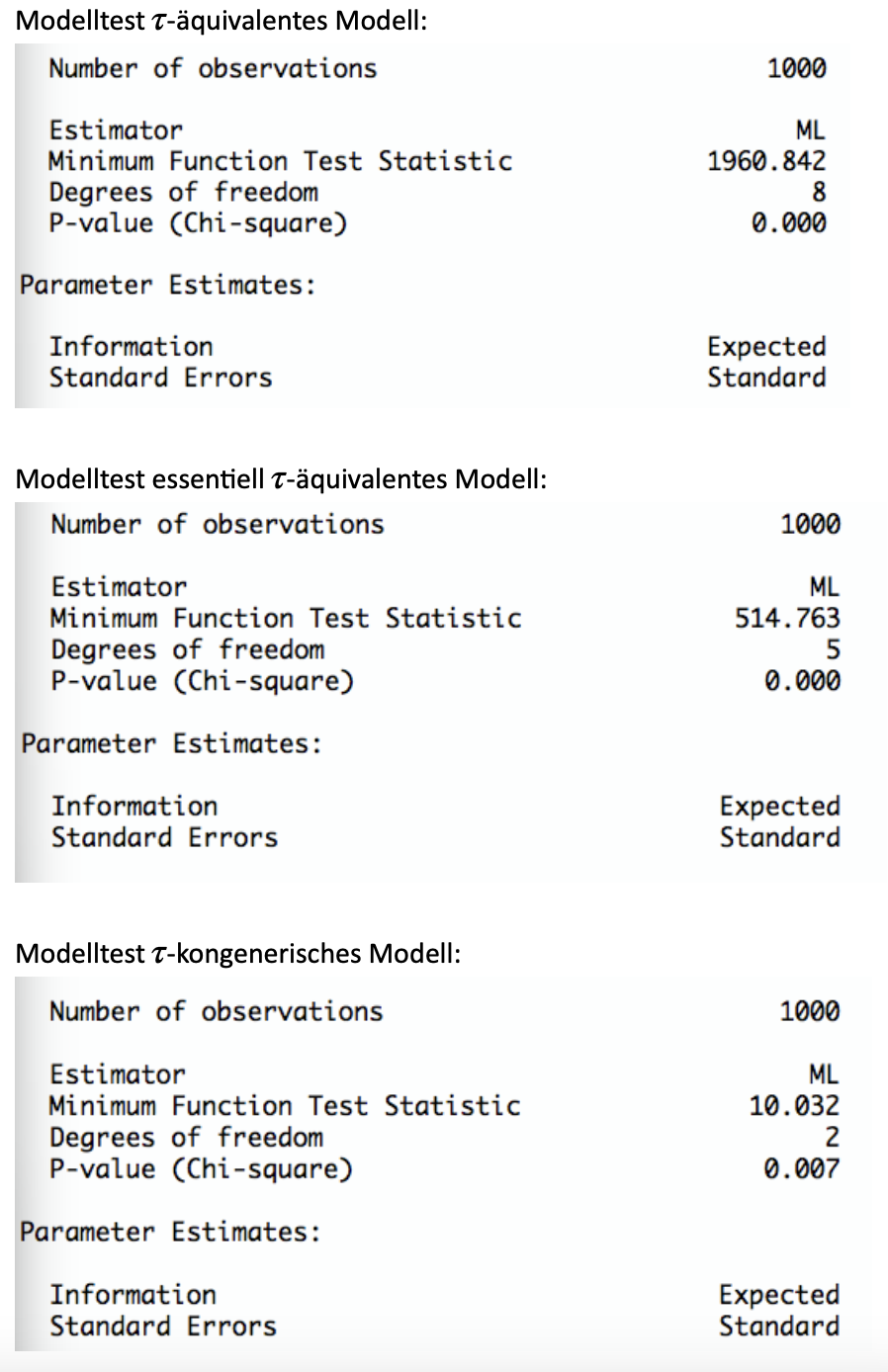
    Welche Modelle werden abgelehnt? Welche Modelle werden nicht abgelehnt? Wie würden Sie weiter vorgehen?

    Alle eindimensionalen Modelle werden abgelehnt, da alle p-Werte < 0.05 sind.

    Möglichkeiten für weiteres Vorgehen:
    • Überprüfen, ob interpretierbares mehrdimensionales Modell angenommen werden kann
    • Überprüfen, ob einzelne Items Probleme verursachen
    • Theorie revidieren

  7. Sie haben einen psychologischen Test entworfen und wollen überprüfen, welchem testtheoretischen Modell dessen Items folgen. Sie erhalten folgende Outputs:

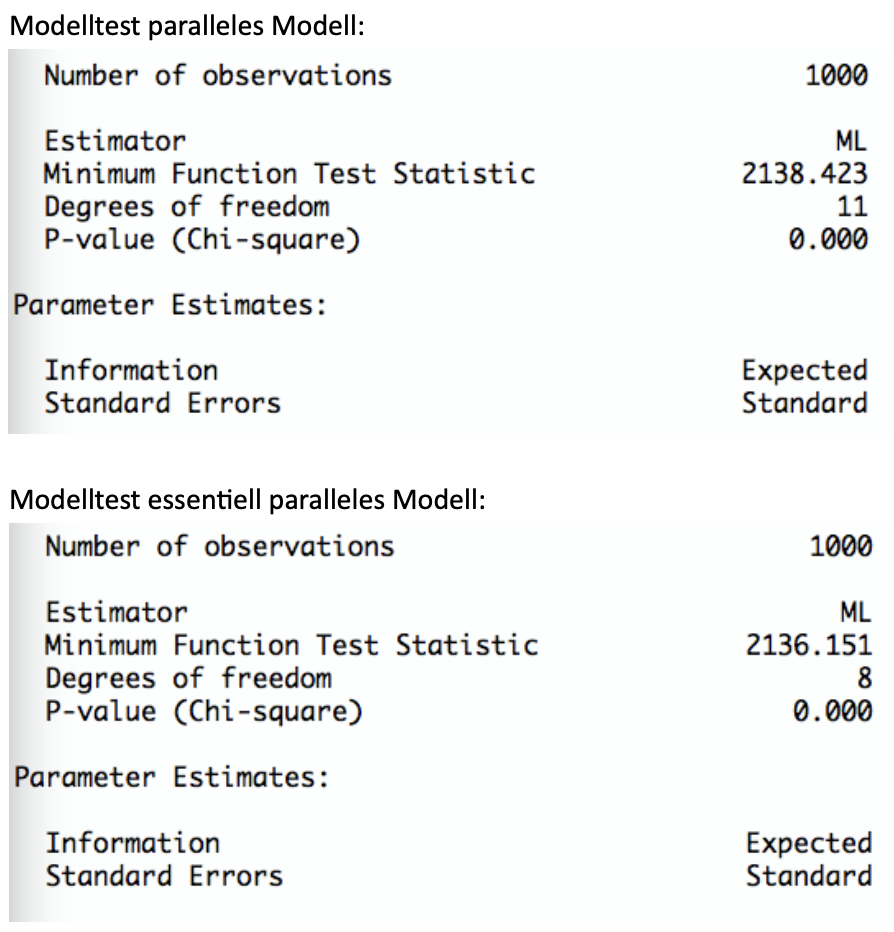
    Welche Modelle werden abgelehnt? Welche Modelle werden nicht abgelehnt? Wie würden Sie weiter vorgehen?

    Paralleles und essentiell paralleles Modell werden abgelehnt, da hier die p-Werte < 0.05 sind.
    Nicht abgelehnt werden \(\tau\)-äquivalentes, essentiell \(\tau\)-äquivalentes und \(\tau\)-kongenerisches Modell, da hier die p-Werte > 0.05 sind.

    Weiteres Vorgehen:

    Entweder für das strengste der nicht abgelehnten Modelle entscheiden, d.h. für das \(\tau\)-äquivalente Modell.
    Niedrigere Komplexität des Modells, aber höheres Risiko potentieller Fehlentscheidung bei der Überprüfung der zusätzlichen Annahmen

    Oder für das am wenigsten strenge der nicht abgelehnten Modelle entscheiden, d.h. für das \(\tau\)-kongenerische Modell. Vermeidung von potentiellen Fehlentscheidungen bei der Überprüfung der zusätzlichen Annahmen der strengeren Modelle, aber höhere Komplexität des Modells, d.h. mehr Parameter müssen geschätzt werden

  8. Sie betrachten einen Test mit vier Items, von denen Sie aus vorangehenden Modelltests wissen, dass Sie einem parallelen Modell folgen. Sie erhalten folgenden Output mit Schätzwerten für die Parameter des Modells:

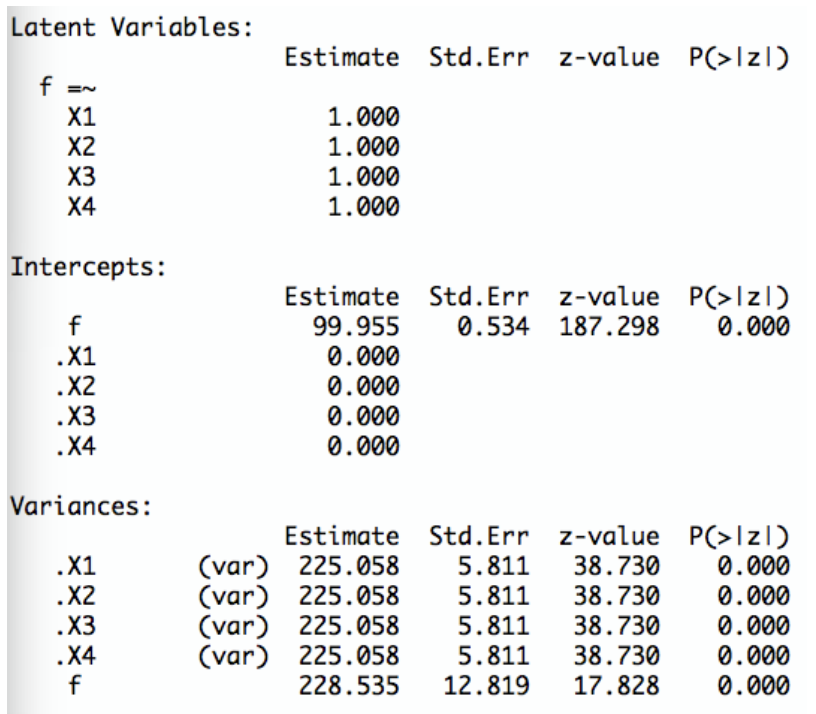
    1. Was ist der Schätzwert für den Erwartungswert \(E(\theta)\) der latenten Variable? Wie kann dieser Wert interpretiert werden?

      Der Schätzwert für \(E(\theta)\) ist 99.955. Dies ist der Schätzwert für den Mittelwert der latenten Variable in der Population.

    2. Was ist der Schätzwert für die Varianz \(Var(\theta)\) der latenten Variable? Wie kann dieser Wert interpretiert werden?

      Der Schätzwert für \(Var(\theta)\) ist 228.535. Dies ist der Schätzwert für die Varianz der latenten Variable in der Population.

    3. Was sind die Schätzwerte für die Varianzen \(Var(\epsilon_{i})\) der Fehlervariablen?

    :::{.callout-tip collapse=true} # Lösung Der Schätzwert für \(Var(\epsilon_{i})\) ist 225.058 für alle Items i :::

  9. Sie betrachten einen Test mit vier Items, von denen Sie aus vorangehenden Modelltests wissen, dass Sie einem essentiell \(\tau\)-äquivalenten Modell folgen. Sie erhalten folgenden Output mit Schätzwerten für die Parameter des Modells:

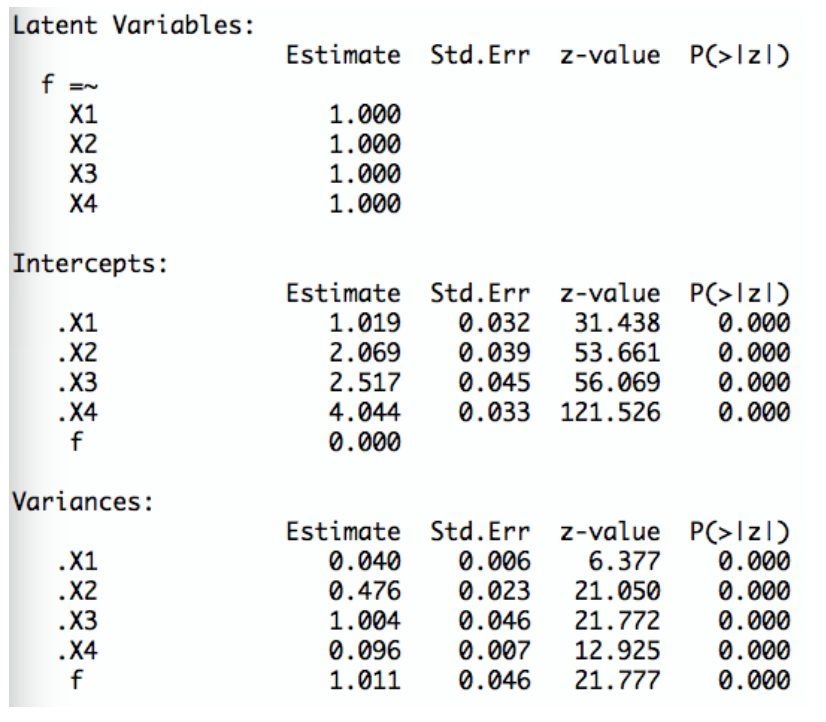
    1. Was sind die Schätzwerte für die Schwierigkeitsparameter \(\sigma_{i}\)? Wie können diese Werte interpretiert werden?

      Der Schätzwert für \(\sigma_{1}\) ist 1.019
      Der Schätzwert für \(\sigma_{2}\) ist 2.069
      Der Schätzwert für \(\sigma_{3}\) ist 2.517
      Der Schätzwert für \(\sigma_{4}\) ist 4.044

      Dies sind die Schätzwerte für die Erwartungswerte der vier Items bei einer Person mit einer durchschnittlichen Ausprägung auf der latenten Variable.

    2. Was sind die Schätzwerte für die Varianzen \(Var(\epsilon_{i})\) der Fehlervariablen?

      Der Schätzwert für \(Var(\epsilon_{1})\) ist 0.040
      Der Schätzwert für \(Var(\epsilon_{2})\) ist 0.476
      Der Schätzwert für \(Var(\epsilon_{3})\) ist 1.004
      Der Schätzwert für \(Var(\epsilon_{4})\) ist 0.096

    3. Was ist der Schätzwert für die Varianz \(Var(\theta)\) der latenten Variable? Wie kann dieser Wert interpretiert werden?

      Der Schätzwert für \(Var(\theta)\) ist 1.011. Dies ist der Schätzwert für die Varianz der latenten Variable in der Population.

    4. Warum ist der Wert für den Erwartungswert \(E(\theta)\) der latenten Variable auf 0 gesetzt?

      Wegen der Normierung \(E(\theta)\) im essentiell \(\tau\)-äquivalenten Modell.

  10. Sie betrachten einen Test mit vier Items, von denen Sie aus vorangehenden Modelltests wissen, dass Sie einem \(\tau\)-kongenerischen Modell folgen. Sie erhalten folgenden Output mit Schätzwerten für die Parameter des Modells:

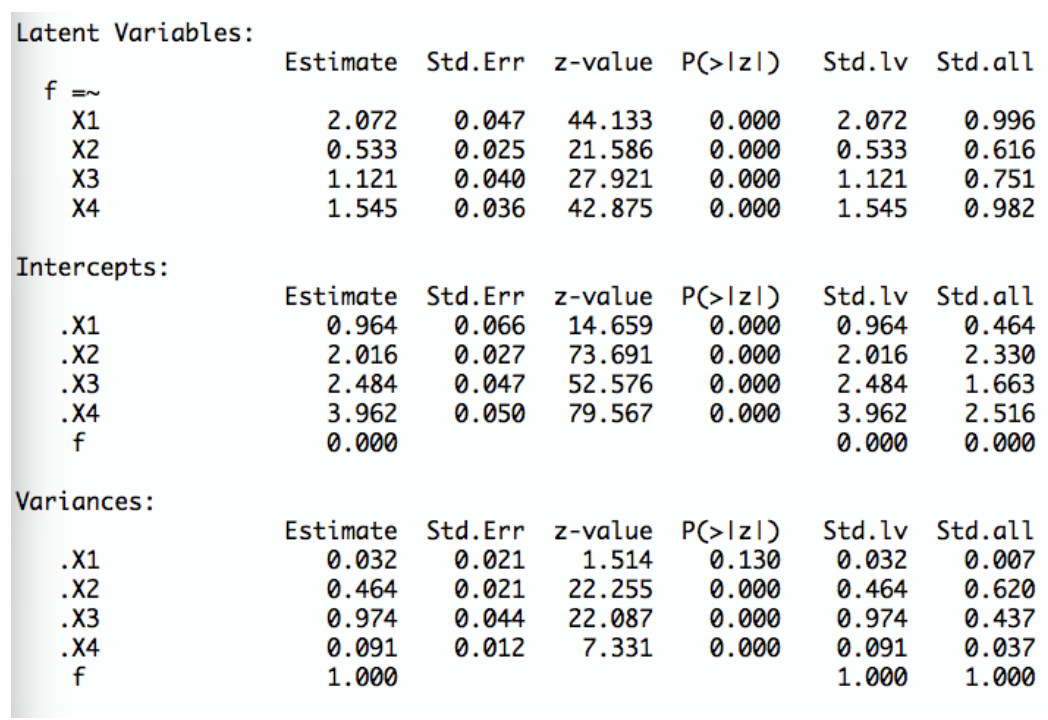
    1. Was sind die Schätzwerte für die Schwierigkeitsparameter \(\sigma_{i}\)? Wie können diese Werte interpretiert werden?

      Der Schätzwert für \(\sigma_{1}\) ist 0.964
      Der Schätzwert für \(\sigma_{2}\) ist 2.016
      Der Schätzwert für \(\sigma_{3}\) ist 2.484
      Der Schätzwert für \(\sigma_{4}\) ist 3.962
      Dies sind die Schätzwerte für die Erwartungswerte der vier Items

    2. Was sind die Schätzwerte für die Varianzen \(Var(\epsilon_{i})\) der Fehlervariablen?

      Der Schätzwert für \(Var(\epsilon_{1})\) ist 0.032
      Der Schätzwert für \(Var(\epsilon_{2})\) ist 0.464
      Der Schätzwert für \(Var(\epsilon_{3})\) ist 0.974
      Der Schätzwert für \(Var(\epsilon_{4})\) ist 0.091

    3. Was sind die Schätzwerte für die Steigungsparameter \(\beta_{i}\)? Interpretieren Sie den Steigungsparameter des zweiten Items

      Der Schätzwert für \(\beta_{1}\) ist 2.072
      Der Schätzwert für \(\beta_{2}\) ist 0.533
      Der Schätzwert für \(\beta_{3}\) ist 1.121
      Der Schätzwert für \(\beta_{4}\) ist 1.545

      Falls sich die latente Variable um eine Einheit erhöht, erhöht sich die durchschnittliche Itemantwort auf Item 2 um 0.533 Einheiten

    4. Warum ist der Wert für den Erwartungswert \(E(\theta)\) der latenten Variable auf 0 gesetzt? Warum der Wert für die Varianz \(Var(\theta)\) der latenten Variable auf 1?

      Wegen den Normierungen \(E(\theta) = 0\) und \(Var(\theta) = 1\) im \(\tau\)-kongenerischen Modell.