Übungsblatt 1: Gemischte Lineare Modelle (LMMs)

Veröffentlichungsdatum

7. November 2024

Datensatz

Für die folgenden Aufgaben verwenden wir erneut den Datensatz HSB.csv. Wir betrachten ein hierarchisches Modell mit zwei Ebenen (Schüler geschachtelt in Schulen).

Vorbereitungen:

  1. Laden Sie sich den Datensatz HSB.csv hier herunter und verschieben Sie die Datei in Ihren Projektordner. Öffnen Sie danach RStudio, indem Sie auf die .Rproj Verknüpfung Ihres Projekts doppelklicken.

  2. Pakete laden (ggf. müssen die Pakete zuerst installieren, erst danach klappt der library()-Befehl):

library(lme4) # für die Befehle der Gemischten linearen Modelle
library(lmerTest) # dies dient dazu, p-Werte anzuzeigen
library(sjPlot) # für die Grafiken
  1. Datensatz einlesen:
hsb <- read.csv2("HSB.csv")

Nachfolgende Variablen sind ggf. für die zu bearbeitenden Aufgabenstellungen relevant:

  • School: ID für jeweilige Schule
  • SES: Sozioökonomischer Status jeder Schülerin
  • MathAch: Mathematikleistung jeder Schülerin (höher -> besser)
  • Minority: Entstammt eine Schülerin einer Minderheit (Nein, Ja)
  • Sex: Geschlecht der Schülerin (Männlich, Weiblich)
  • MeanSES: Mittelwert im SES für Schülerin der jeweiligen Schule
  • Sector: Schulart (Katholische Schule, Öffentliche Schule)
  • DISCLIM: “Diskriminierungsklima” der jeweiligen Schule (höhere Werte -> stärkere Diskriminierung in der Schule
  • Size: Größe der Schule

Aufgaben

Aufgabe 1:

Untersuchen Sie im Folgenden den Einfluss des Diskriminierungsklimas der Schulen und der jeweiligen Zugehörigkeit zu einer Minderheit auf die Mathematikleistung.

  1. Wirkt sich die Zugehörigkeit zu einer Minorität nachteilig auf die Mathematiknote aus?
  2. Welche Rolle spielt das Diskriminierungsklima bei Schülerinnen, die keiner Minderheit angehören?
  3. Welche Rolle spielt das Diskriminierungsklima bei Schülerinnen einer Minderheit?

  1. Stellen Sie zunächst die Gleichungen für ein Modell auf, mit dem Sie alle Teilfragen beantworten können.

    Modellgleichungen: \[ \begin{aligned} &\text{Lvl 1: }& MathAch_{ij} &= \beta_{0j} + \beta_{1j}Minority_{ij} + r_{ij} \\ &\text{Lvl 2: }& \beta_{0j} &= \gamma_{00} + \gamma_{01}DISCLIM_j + u_{0j} \\ &\text{ } & \beta_{1j} &= \gamma_{10} + \gamma_{11}DISCLIM_j + u_{1j} \\ \hline &\text{Mixed: }& MathAch_{ij} &= \gamma_{00} + \gamma_{10}Minority_{ij} + \gamma_{01}DISCLIM_j + \gamma_{11}Minority_{ij}DISCLIM_j + u_{0j} + u_{1j}Minority_{ij} + r_{ij} \end{aligned} \]

  2. Übertragen Sie das Modell dann in die Formelsyntax des lme4 Pakets und schätzen Sie es in R. Interpretieren Sie.

    r1 <- lmer(MathAch ~ 1 + Minority + DISCLIM + Minority:DISCLIM + 
    (1 + Minority | School), hsb)
summary(r1)
    Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: MathAch ~ 1 + Minority + DISCLIM + Minority:DISCLIM + (1 + Minority |  
    School)
   Data: hsb

REML criterion at convergence: 46736.9

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-2.92091 -0.73346  0.03333  0.75583  2.85158 

Random effects:
 Groups   Name        Variance Std.Dev. Corr 
 School   (Intercept)  4.787   2.188         
          MinorityYes  1.387   1.178    -0.15
 Residual             37.390   6.115         
Number of obs: 7185, groups:  School, 160

Fixed effects:
                    Estimate Std. Error       df t value Pr(>|t|)    
(Intercept)          13.6489     0.1984 138.9502  68.791  < 2e-16 ***
MinorityYes          -3.7718     0.2366 117.2847 -15.942  < 2e-16 ***
DISCLIM              -0.9919     0.2079 144.9966  -4.771 4.42e-06 ***
MinorityYes:DISCLIM  -1.3480     0.2401 124.6671  -5.613 1.22e-07 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
            (Intr) MnrtyY DISCLI
MinorityYes -0.310              
DISCLIM      0.054 -0.035       
MnY:DISCLIM -0.036  0.028 -0.347

    Auf Schulen mit DISCLIM = 0 unterscheiden sich Schülerinnen einer Minderheit von Schülerinnen die keiner Minderheit angehören, in ihrer vorhergesagten Mathematiknote um -3.77. Schüler die keiner Minderheit angehören und an Schulen sind, die sich um 1 im Diskrimierungsklima unterscheiden, unterscheiden sich in Ihrer vorhergesagten Mathematiknote um -0.99. Wenn diese Schülerinnen dabei auch noch einer Minderheit angehören, unterscheidet sich die vorhergesagte Mathematiknote zusätzlich um -1.34. D.h. das Diskrimierungsklima wirkt sich für Minderheiten signifikant stärker negativ auf die Mathematiknote aus als für Schülerinnen die keiner Minderheit angehören.

  3. Veranschaulichen Sie das Modell grafisch. Probieren Sie dabei für das Argument terms mal beide Varianten aus: 1) L1-Prädiktor an erster und L2-Prädiktor an zweiter Stelle (terms = c("Minority", "DISCLIM")), so wie in den Instruktionsvideos und 2) mit umgekehrter Reihenfolge (terms = c("DISCLIM", "Minority")). Welche Variante finden Sie leichter zu interpretieren? (Es gibt natürlich hier keine “richtige” Variante.)

    plot_model(r1, type = "pred", terms = c("Minority", "DISCLIM"))
plot_model(r1, type = "pred", terms = c("DISCLIM", "Minority"))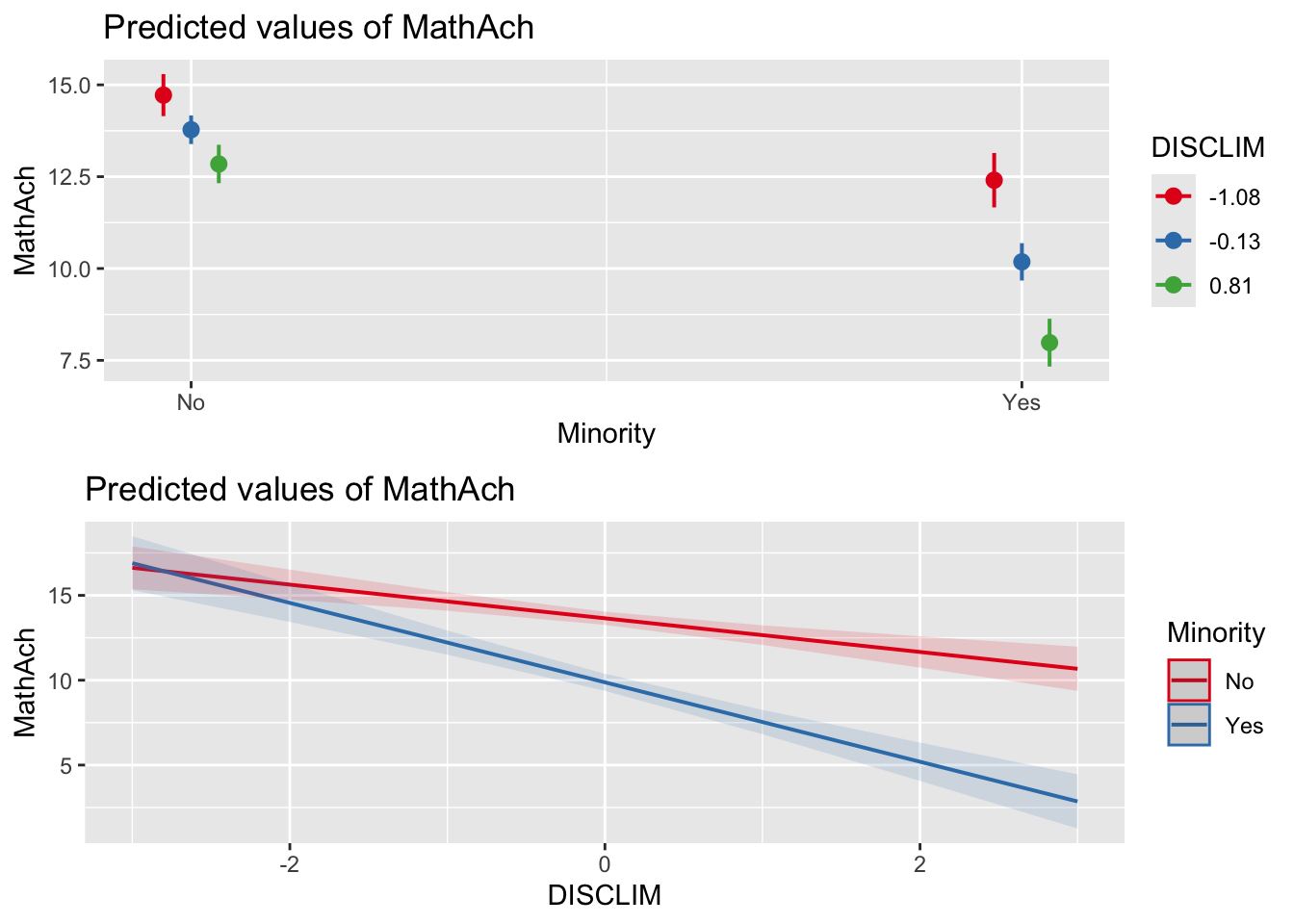

Aufgabe 2. 1

Untersuchen Sie im Folgenden den Einfluss der Schulgröße, der jeweiligen Zugehörigkeit zu einer Minderheit und des jeweiligen Geschlechts auf die Mathematikleistung. Welche Aussagen können Sie über die gefundenen Zusammenhänge treffen? Stellen Sie zunächst die Gleichungen für ein Modell auf, das Aussagen über die gesuchten Zusammenhänge erlaubt. Schätzen Sie dann das Modell und versuchen Sie, die Zusammenhänge grafisch zu veranschaulichen.

Hinweis 1: Man koennte auf Lvl 1 noch den Interaktionseffekt Sex x Minority mit aufnehmen und hätte dann noch ein \(\beta_{3j}\) und eine vierte Lvl 2 Gleichung. Das ist hier jetzt nicht zwingend notwending - ausserdem erhöt sich die Komplexität durch 3-fach-Interaktionen so enorm.

Hinweis 2: Size ist im Datensatz unzentriert. Eine Empfehlung wäre, eine Grand-Mean-Zentrierung vorzunehmen. Das ist deshalb sinnvoll, da sonst alle Aussagen auf Schulen mit Grösse = 0 bezogen wären, was keine relevante Bezugsgruppefür die Interpretation der anderen Effekte ist. Nach der Zentrierung beziehen sich die Aussagen auf Schulen mit durchschnittlicher Schülerzahl. Eine zweite Empfehlung wäre noch, Size so zu verändern, dass ein Unterschied von 1 einer Differenz von 100 Schülerinnen entspricht. Warum? Bedenken Sie, dass Sie sich die Interpretation des Slopes auf einen Unterschied von 1 bezieht. Ohne die Veränderung würden Sie also zwei Schulen vergleichen, die sich um eine Schülerin in ihrer Größe unterscheiden. Mit der empfohlenen Veränderung entspricht ein Unterschied von 1 in der neuen Variable einem Größenunterschied von 100 Personen. Auch hier gibt es keine “richtige” Variante.

Modellgleichungen: \[ \begin{aligned} &\text{Lvl 1: } &MathAch_{ij} &= \beta_{0j} + \beta_{1j}Sex_{ij} + \beta_{2j}Minority_{ij} + r_{ij} \\ &\text{Lvl 2: } &\beta_{0j} &= \gamma_{00} + \gamma_{01}Size.100.c_j + u_{0j} \\ &\text{} &\beta_{1j} &= \gamma_{10} + \gamma_{11}Size.100.c_j + u_{1j} \\ &\text{} &\beta_{2j} &= \gamma_{20} + \gamma_{21}Size.100.c_j + u_{2j} \end{aligned} \]

hsb$Size.100.c <- (hsb$Size - mean(hsb$Size))/100
r2 <- lmer(MathAch ~ 1 + Sex + Minority + Size.100.c +
    Size.100.c:Sex + Size.100.c:Minority + (1 + Sex + Minority | School), hsb)
summary(r2)
Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: MathAch ~ 1 + Sex + Minority + Size.100.c + Size.100.c:Sex +  
    Size.100.c:Minority + (1 + Sex + Minority | School)
   Data: hsb

REML criterion at convergence: 46727.5

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-2.92751 -0.72950  0.03707  0.76592  2.57546 

Random effects:
 Groups   Name        Variance Std.Dev. Corr       
 School   (Intercept)  4.8897  2.2113              
          SexMale      0.5575  0.7467    0.10      
          MinorityYes  2.4885  1.5775    0.28 -0.10
 Residual             36.9707  6.0804              
Number of obs: 7185, groups:  School, 160

Fixed effects:
                         Estimate Std. Error         df t value Pr(>|t|)    
(Intercept)             13.014461   0.215506 137.074074  60.390  < 2e-16 ***
SexMale                  1.366253   0.181539 117.621420   7.526 1.16e-11 ***
MinorityYes             -3.678761   0.261346 115.622479 -14.076  < 2e-16 ***
Size.100.c              -0.006985   0.035078 147.356617  -0.199 0.842427    
SexMale:Size.100.c       0.062659   0.028804 129.096117   2.175 0.031422 *  
MinorityYes:Size.100.c  -0.147572   0.041171 124.162823  -3.584 0.000484 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
            (Intr) SexMal MnrtyY S.100. SM:S.1
SexMale     -0.325                            
MinorityYes -0.099 -0.024                     
Size.100.c  -0.040  0.035 -0.018              
SxMl:S.100.  0.039 -0.146  0.006 -0.298       
MnrY:S.100. -0.020  0.007 -0.089 -0.169 -0.017
  • Die vorhergesagte Mathematiknote für Frauen (Sex = Female), die keiner Minorität angehören (Minority = No) und an durchschnittlich großen Schulen sind (Size.100.c = 0) ist 13.01 und signifikant von 0 verschieden.
  • An Schulen mit durchschnittlicher Größe (Size.100.c = 0) unterscheiden sich Männer und Frauen die keiner Minderheit angehören (Minority = 0) in ihrer vorhergesagten Mathematiknote um 1.37 (signifikant).
  • An Schulen mit durchschnittlicher Größe (Size.100.c = 0) unterscheiden sich weibliche Schüler einer Minorität von weiblichen nicht-Minoritäts-Schülern (Sex = Female) in ihrer vorhergesagten Mathematiknote um -3.68 (signifikant).
  • Die Schulgröße macht für weibliche Schüler (Sex = Female), die keiner Minorität angehören (Minority = No) keinen Unterschied in der vorhergesagten Mathematiknote (Slope von -0.007 ist nicht signifikant).
  • Für männliche Schüler (Sex = Male), die keiner Minorität angehören (Minority = 0) ist dieser Zusammenhang jedoch signifikant unterschiedlich und um 0.0627 signifikant größer als bei den eben erwähnten Frauen. Ob der Gesamtslope von Size.100.c für nicht-Minoritäts-Männer noch signifikant ist, lässt sich nicht sagen. Er würde durch die Addition des “Haupteffekts” -0.007 und der Interaktion 0.0627 entstehen. Die Summe ist 0.0557, ob das signifikant von 0 verschieden ist, wird nicht geprüft.
  • Für weibliche Schüler (Sex = Female), die einer Minorität angehören (Minority = Yes) wird vom Slope von -0.007 der Schulgröße noch der Interaktionseffekt von -0.148 abgezogen (dieser Unterschied im Slope ist signifikant). Ob die Summer dieser beiden Werte wieder signifikant ist, kann auch wieder nicht gesagt werden, da das nicht geprüft wird.
  • Für weibliche Schüler und Schüler einer Minderheit wirkt sich eine steigende Schulgröße also zunehmend negativ aus.
plot_model(r2, type = 'pred', terms = c('Size.100.c', 'Minority', 'Sex'))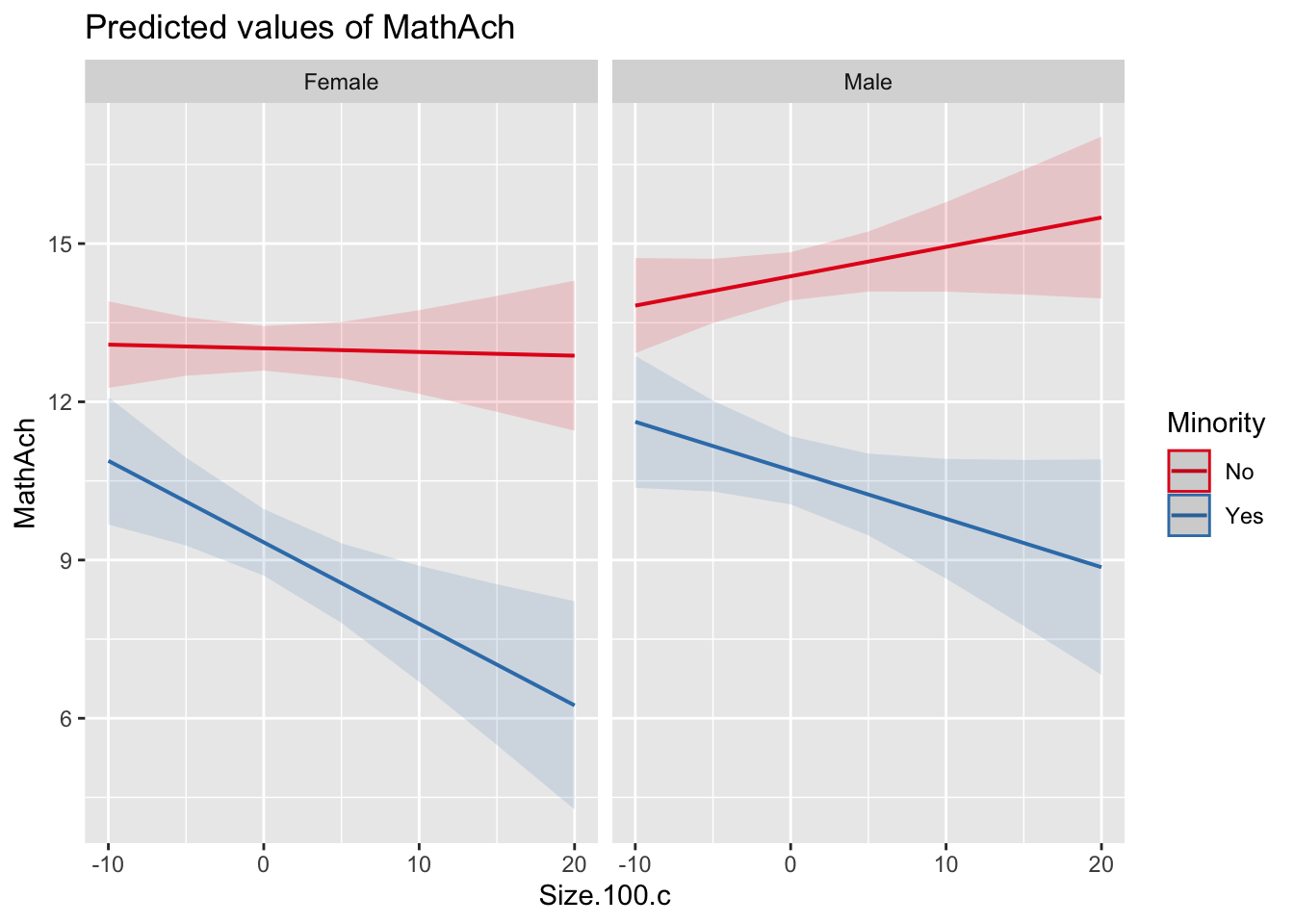

Fußnoten

  1. Sobald mehr als zwei Variablen im Spiel sind, wird es enorm komplex. Die Aufgabe ist nicht dazu gedacht, zu demonstrieren, dass es eine “richtige” Lösung gibt. Vielmehr möchten wir Sie anregen, hier mal unterschiedliche Wege auszuprobieren und zu sehen, welche Fragen Sie damit beantworten könnten.↩︎