Übungsblatt 1: Lasso und Logistische Regression

Veröffentlichungsdatum

22. Oktober 2024

In diesem Übungsblatt wollen wir uns nochmal verstärkt mit regularisierten (Lasso) und nicht regularisierten linearen Modellen in R beschäftigen. Wir besprechen den Unterschied am Beispiel einer logistischen Regression mit dem aus der Vorlesung im Wintersemester bekannten Titanic Datensatzes. Der Datensatz ist in R im Paket rpart.plot enthalten, wir stellen die Datei Titanic.csv jedoch auch hier als Download zur Verfügung.

Titanic <- read.csv2("Titanic.csv")

Um die Analyse etwas zu vereinfachen, entfernen wir aus dem Datensatz alle Beobachtungen mit fehlenden Werten.

Titanic <- Titanic[complete.cases(Titanic), ]

Im Folgenden überschreiben wir die Variablennamen mit den deutschen Bezeichnungen, die wir auch im Wintersemester in der Vorlesung verwendet haben.

names(Titanic) <- c("Befoerderungsklasse", "Ueberlebt", "Geschlecht", "Alter", 
  "Geschwister_Partner", "Eltern_Kinder")

Die 3 Variablen Befoerderungsklasse, Ueberlebt und Geschlecht enthalten Text (d.h. es sind sogenannte “character” Variablen) und müssen für die Analysen in R als Faktor kodiert werden. Wir nutzen diese Gelegenheit um zusätzlich die englischen Labels durch deutsche Labels zu ersetzen.

str(Titanic)

'data.frame':   1046 obs. of  6 variables:
 $ Befoerderungsklasse: chr  "1st" "1st" "1st" "1st" ...
 $ Ueberlebt          : chr  "survived" "survived" "died" "died" ...
 $ Geschlecht         : chr  "female" "male" "female" "male" ...
 $ Alter              : num  29 0.917 2 30 25 ...
 $ Geschwister_Partner: int  0 1 1 1 1 0 1 0 2 0 ...
 $ Eltern_Kinder      : int  0 2 2 2 2 0 0 0 0 0 ...

Titanic$Befoerderungsklasse <- factor(Titanic$Befoerderungsklasse, 
  levels = c("1st", "2nd", "3rd"), labels = c("1.", "2.", "3."))
Titanic$Ueberlebt <- factor(Titanic$Ueberlebt, levels = c("died", "survived"), 
  labels = c("Tod", "Leben"))
Titanic$Geschlecht <- factor(Titanic$Geschlecht, levels = c("female", "male"), 
  labels = c("weiblich", "maennlich"))

str(Titanic)

'data.frame':   1046 obs. of  6 variables:
 $ Befoerderungsklasse: Factor w/ 3 levels "1.","2.","3.": 1 1 1 1 1 1 1 1 1 1 ...
 $ Ueberlebt          : Factor w/ 2 levels "Tod","Leben": 2 2 1 1 1 2 2 1 2 1 ...
 $ Geschlecht         : Factor w/ 2 levels "weiblich","maennlich": 1 2 1 2 1 2 1 2 1 2 ...
 $ Alter              : num  29 0.917 2 30 25 ...
 $ Geschwister_Partner: int  0 1 1 1 1 0 1 0 2 0 ...
 $ Eltern_Kinder      : int  0 2 2 2 2 0 0 0 0 0 ...

Wir laden das mlr3verse und erstellen einen Klassifikations-Task bei dem vorhergesagt werden soll, ob eine Person das Schiffsunglück überlegt. Wie bei Klassifikationsaufgaben üblich, stratifizieren wir den Task anhand der Zielvariable.

# Paket laden
library(mlr3verse)

Loading required package: mlr3

# Task erstellen
Titanic_task <- as_task_classif(Titanic, id = "titanic", target = "Ueberlebt",
  positive = "Leben")

# Stratifizierung
Titanic_task$col_roles$stratum <- "Ueberlebt"

Wir definieren einen Featureless Learner, eine logistische Regression und ein Lasso. Das Lasso Modell kann nicht automatisch mit Faktorvariablen umgehen. Wir kombinieren es daher mit einer encode Pipeline, die automatisch Dummyvariablen erstellt. Um das Lasso Modell benutzen zu können, muss das glmnet R Paket installiert sein. Sowohl bei der logistischen Regression als auch beim Lasso stellen wir ein, dass der Learner immer Wahrscheinlichkeiten anstatt konkrete Werte für die Zielvariable vorhersagen.

# Learner definieren
featureless <- lrn("classif.featureless")
logreg <- lrn("classif.log_reg", predict_type = "prob")
lasso <- as_learner(po("encode", method = "treatment") %>>%
    lrn("classif.cv_glmnet", predict_type = "prob"))

Wir berechnen einen Benchmark mit allen drei Learnern um einen Überblick über die Prädiktive Performance der Modelle zu erhalten.

set.seed(1)
# Benchmark Experiment
Titanic_design <- benchmark_grid(
  tasks = Titanic_task, 
  learners = list(featureless, logreg, lasso),
  resamplings = rsmp("repeated_cv", folds = 10, repeats = 10)
)
Titanic_bm <- benchmark(Titanic_design)

Hier schauen wir uns das Ergebnis grafisch an. In diesem Beispiel scheint die Performance bezüglich des MMCE für die logistische Regression und das Lasso ähnlich zu sein.

# Ergebnis plotten
autoplot(Titanic_bm, measure = msr("classif.ce"))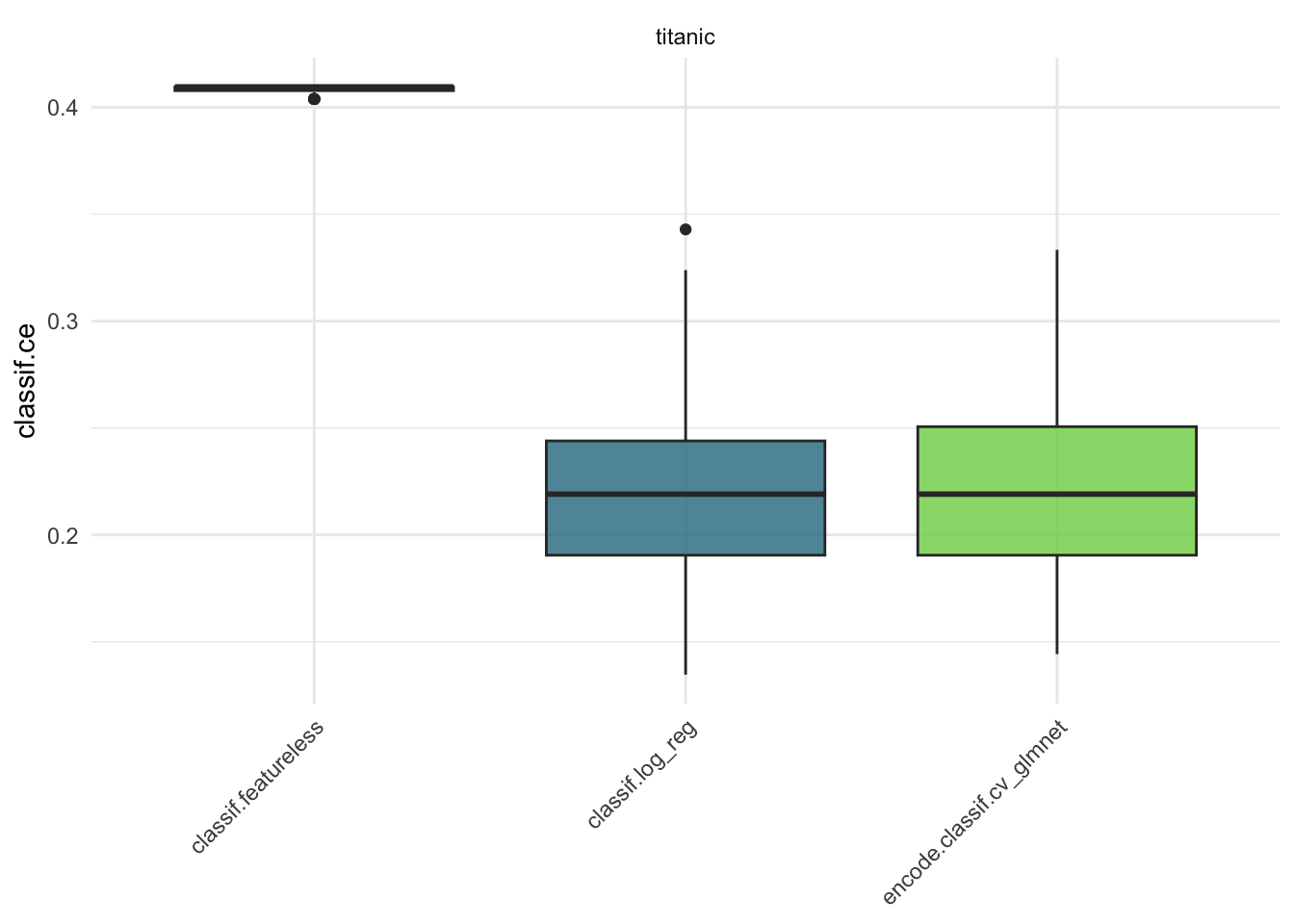

Als Nächstes trainieren wir sowohl die logistische Regression als auch das Lasso auf dem vollständigen Datensatz / Task. Diese Modelle können später dazu genutzt werden, für konkrete Personen Vorhersagen zu berechnen. Da beim Training des Lassos der Regularisierungsparameter \(\lambda\) automatisch mithilfe von Cross-Validation getuned wird und dieser Vorgang eine zufällige Aufteilung in Trainings- und Testsets enthält, setzen wir einen Seed um die Parameterschätzungen reproduzierbar zu machen.

set.seed(2)
logreg$train(Titanic_task)
lasso$train(Titanic_task)

Der folgende Code extrahiert die beiden trainierten Modelle. Die logistische Regression wurde intern mit der glm Funktion geschätzt. Für das Lasso wurde intern die Funktion cv.glmnet aus dem glmnet Paket verwendet.

logreg_model <- logreg$model
lasso_model <- lasso$model$classif.cv_glmnet$model

Der folgende Output zeigt die Parameterschätzungen für die Koeffizienten aus dem logistischen Regressionsmodell.

coef(logreg_model)

          (Intercept)                 Alter Befoerderungsklasse2. 
           3.90679127           -0.03948868           -1.36675654 
Befoerderungsklasse3.         Eltern_Kinder   Geschlechtmaennlich 
          -2.35202228            0.07436088           -2.55685974 
  Geschwister_Partner 
          -0.35291462

Der folgende Output zeigt die Parameterschätzungen für die Koeffizienten aus dem Lasso Modell.

coef(lasso_model)

7 x 1 sparse Matrix of class "dgCMatrix"
                                s1
(Intercept)             1.89536907
Alter                  -0.01089698
Eltern_Kinder           .         
Geschwister_Partner    -0.02865026
Befoerderungsklasse.2. -0.31556068
Befoerderungsklasse.3. -1.20997024
Geschlecht.maennlich   -2.14619130

Übungsaufgaben

Aufgabe 1

Beschreiben Sie anhand eines Vergleichs der Parameterschätzungen der beiden Modelle, welchen Effekt die Regularisierung im Lasso Modell auf die Schätzwerte hat.

Lösung

Die Regularisierung führt dazu, dass manche Parameter auf den Wert 0 geschätzt werden (hier: Eltern_Kinder). Auch für die restlichen Parameter, die nicht exakt auf den Wert 0 geschätzt wurden, sind die Parameterschätzungen im Lasso Modell im Betrag kleiner (d.h. näher an 0) als in der nicht regularisierten logistischen Regression.

Aufgabe 2

Interpretieren Sie den Schätzwert für den Koeffizient Geschlechtmaennlich in beiden Modellen. Geben Sie sowohl die Interpretation bzgl. der Odds als auch bezüglich der Log-Odds an.

Lösung

Die erwarteten Odds das Titanic Unglück zu überleben sind im Mittel um den Faktor exp(-2.56) (für Lasso: exp(-2.15)) höher für einen Mann als für eine Frau (wenn die Werte auf allen anderen Prädiktoren gleich sind).

Die erwarteten Log-Odds das Titanic Unglück zu überleben sind im Mittel um -2.56 (für Lasso: -2.15) höher für einen Mann als für eine Frau (wenn die Werte auf allen anderen Prädiktoren gleich sind).

Aufgabe 3

Berechnen Sie für beide Modelle die geschätzte Wahrscheinlichkeit, dass “Jack” aus dem Film “Titanic” das Schiffsunglück überlebt:

Wir nehmen an, dass Jack 20 Jahre alt ist und alleine in der 3. Klasse reist.

Lösung

Logistische Regression:

# manuell
logistic <- function(v) {
  exp(v) / (1 + exp(v))
}
logistic(
  3.91 - 0.04 * 20 - 1.37 * 0 - 2.35 * 1 + 0.07 * 0 - 2.56 * 1 - 0.35 * 0
)

[1] 0.1418511

# mit mlr3
logreg$predict_newdata(newdata = 
    data.frame(Alter = 20, Befoerderungsklasse = "3.", Eltern_Kinder = 0,
      Geschlecht = "maennlich", Geschwister_Partner = 0))

<PredictionClassif> for 1 observations:
 row_ids truth response prob.Leben  prob.Tod
       1  <NA>      Tod  0.1428443 0.8571557

Lasso:

# manuell
logistic(
  1.90 - 0.01 * 20 - 0.32 * 0 - 1.21 * 1 + 0 * 0 - 2.15 * 1 - 0.03 * 0
)

[1] 0.159762

# mit mlr3
lasso$predict_newdata(newdata = 
    data.frame(Alter = 20, Befoerderungsklasse = "3.", Eltern_Kinder = 0,
      Geschlecht = "maennlich", Geschwister_Partner = 0))

<PredictionClassif> for 1 observations:
 row_ids truth response prob.Leben  prob.Tod
       1  <NA>      Tod  0.1572634 0.8427366

Bonusaufgabe (Keine Lösung)

Überlegen Sie sich einen DAG für das Titanic Beispiel. Wie würden Sie basierend auf dem DAG den totalen (oder auch den direkten) kausalen Effekt des Geschlechts auf die Überlebenswahrscheinlichkeit schätzen?