library(mlr3verse)
dat <- read.csv2("Bed.csv")
dat$Sex <- factor(dat$Sex)
dat$Bed <- factor(dat$Bed)
task_bed <- as_task_classif(dat, id = "Bed", target = "Bed",
positive = "Ja")
fl <- lrn("classif.featureless")
logreg <- lrn("classif.log_reg", predict_type = "prob")
lasso <- as_learner(po("encode", method = "treatment") %>>%
lrn("classif.cv_glmnet", predict_type = "prob"))
rf <- lrn("classif.ranger", predict_type = "prob")
set.seed(1)
bm_design <- benchmark_grid(
tasks = task_bed,
learners = list(fl, logreg, lasso, rf),
resamplings = rsmp("cv", folds = 10)
)
bm <- benchmark(bm_design)Übungsblatt 2: Abschlussübung zum Thema Machine Learning
Dieses Übungsblatt verwendet den Datensatz Bed.csv, den Sie hier herunterladen können. Für die Variable Bed wurden Studienteilnehmerinnen gefragt: “Haben Sie heute morgen ihr Bett gemacht?” (Antwortmöglichkeiten: Ja, Nein)
Als mögliche Prädiktoren um die Variable Bed vorherzusagen, enthält der Datensatz 8 Items einer Skala zu Impulsivität (Variablennamen beginnen mit I) und 8 Items einer Skala zu Ordentlichkeit (Variablennamen beginnen mit O), sowie Alter (Age; in Jahren) und Geschlecht (Sex; männlich, weiblich) der Studienteilnehmerinnen. Die Impulsivitäts- und Ordentlichkeititems wurden mit einer 5-stufigen Likert Skala (“starke Ablehnung”, “Ablehnung”, “neutral”, “Zustimmung”, “starke Zustimmung”) erhoben und sind jeweils kodiert von 0 bis 4. Alle Items sind im Datensatz so kodiert, dass höhere Werte für das jeweilige Konstrukt (Ordentlichkeit bzw. Impulsivität) sprechen. Items die dafür umkodiert wurden sind mit “R” im Variablennamen markiert.
Der Wortlaut der Impulsivitäts- und Ordentlichkeitsitems lautet:
I21R_a: Ich lasse mich selten zu übermäßig auf etwas ein.
I51_a: Ich habe Schwierigkeiten meinen Begierden zu widerstehen.
I81R_a: Ich habe wenig Schwierigkeiten, Versuchungen zu widerstehen.
I111_a: Ich esse meist zu viel von meinen Lieblingsspeisen.
I141R_a: Ich gebe selten meinen spontanen Gefühlen nach.
I171_a: Manchmal esse ich, bis mir schlecht wird.
I201_a: Manchmal handle ich aus einem spontanen Gefühl heraus und bereue es später.
I231R_a: Ich bin stets in der Lage meine Gefühle unter Kontrolle zu haben.
O10R_a: Ich lasse mir lieber Entscheidungsmöglichkeiten offen, anstatt alles im Voraus zu planen.
O40_a: Ich halte meine Sachen ordentlich und sauber.
O70R_a: Ich bin kein sehr systematisch vorgehender Mensch.
O100_a: Ich lasse gerne alles an seinem Platz, damit ich weiß, wo es ist.
O130_a: Ich werde wohl niemals fähig sein, Ordnung in mein Leben zu bringen.
O160_a: Ich neige dazu, etwas zu anspruchsvoll oder genau zu sein.
O190R_a: Ich bin beim Putzen nicht pingelig.
O220R_a: Ich verbringe viel Zeit damit, nach Dingen zu suchen, die ich verlegt habe.
Aufgabe 1a
Geben Sie eine Punktschätzung für die erwartete Vorhersageleistung der 3 prädiktiven Modelle logistische Regression, LASSO und Random Forest an. Verwenden Sie den Mean Misclassification Error (MMCE) als Performancemaß und 10-fold Cross-Validation als Resampling Strategie. Verwenden Sie als Seed set.seed(1).
perf <- bm$aggregate(msr("classif.ce"))
perf nr task_id learner_id resampling_id iters classif.ce
<int> <char> <char> <char> <int> <num>
1: 1 Bed classif.featureless cv 10 0.3996267
2: 2 Bed classif.log_reg cv 10 0.3627231
3: 3 Bed encode.classif.cv_glmnet cv 10 0.3690685
4: 4 Bed classif.ranger cv 10 0.3551607
Hidden columns: resample_resultDas Ergebnis der Punktschätzung beträgt \(MMCE_{CV} =0.363\) für die logistische Regression, \(MMCE_{CV} =0.369\) für das Lasso und \(MMCE_{CV} =0.355\) für den Random Forest
Aufgabe 1b
Würden Sie davon ausgehen, dass eines der 3 prädiktiven Modelle den anderen bezogen auf den MMCE überlegen ist? Begründen Sie.
autoplot(bm, measure = msr("classif.ce"))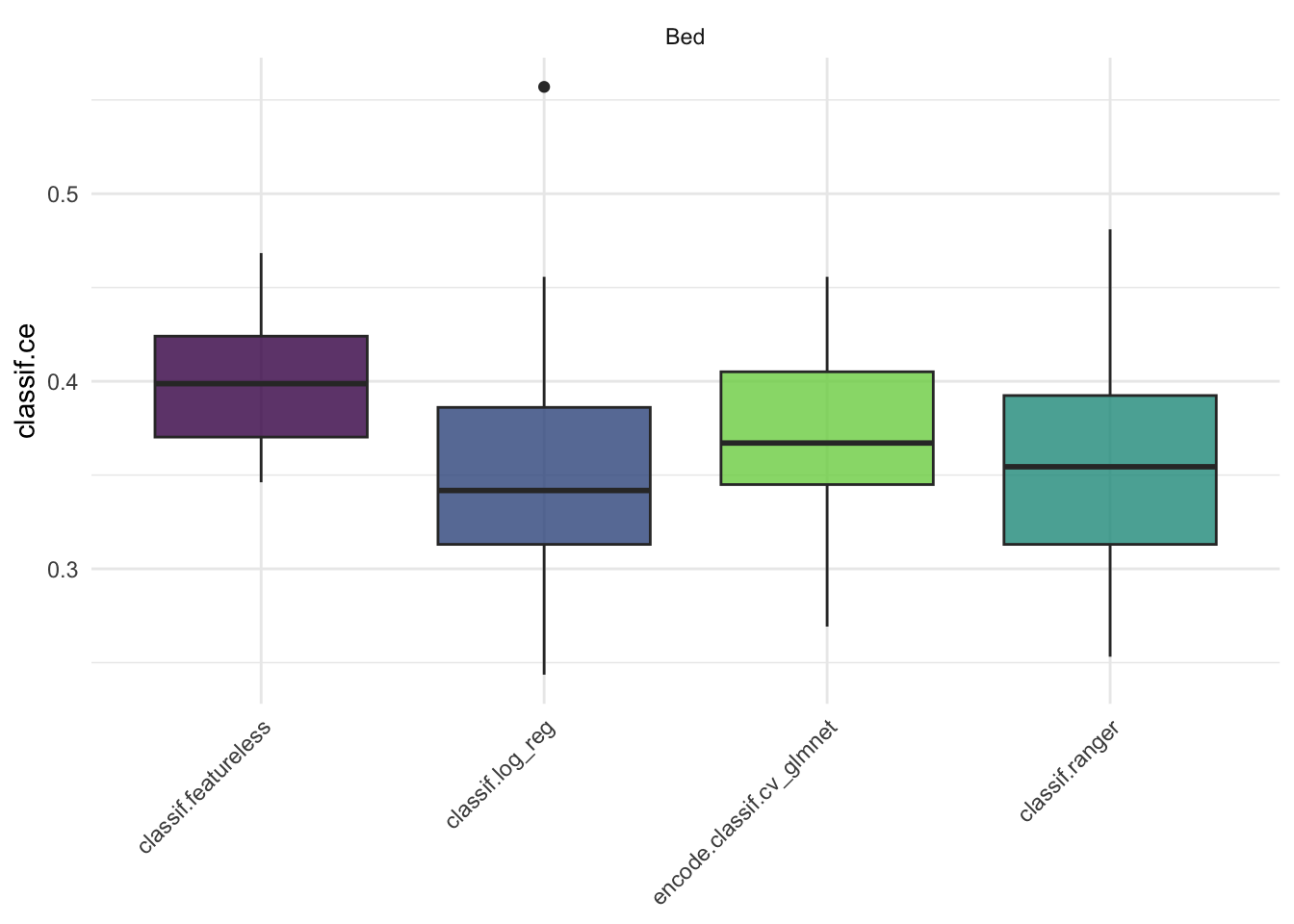
Nein, wir können nicht sicher davon ausgehen, dass eines der 3 prädiktiven Modellen den anderen bezogen auf den MMCE überlegen ist, da sich die Boxplots der Schätzwerte aus den 10 Testsets zwischen den 3 Modellen stark überschneiden.
Aufgabe 1c
Würden Sie davon ausgehen, dass alle 3 prädiktiven Modelle bezogen auf den MMCE besser funktionieren als ein Modell, das für jede Person die häufigste Klasse im Trainingsdatensatz vorhersagt? Begründen Sie.
autoplot(bm, measure = msr("classif.ce"))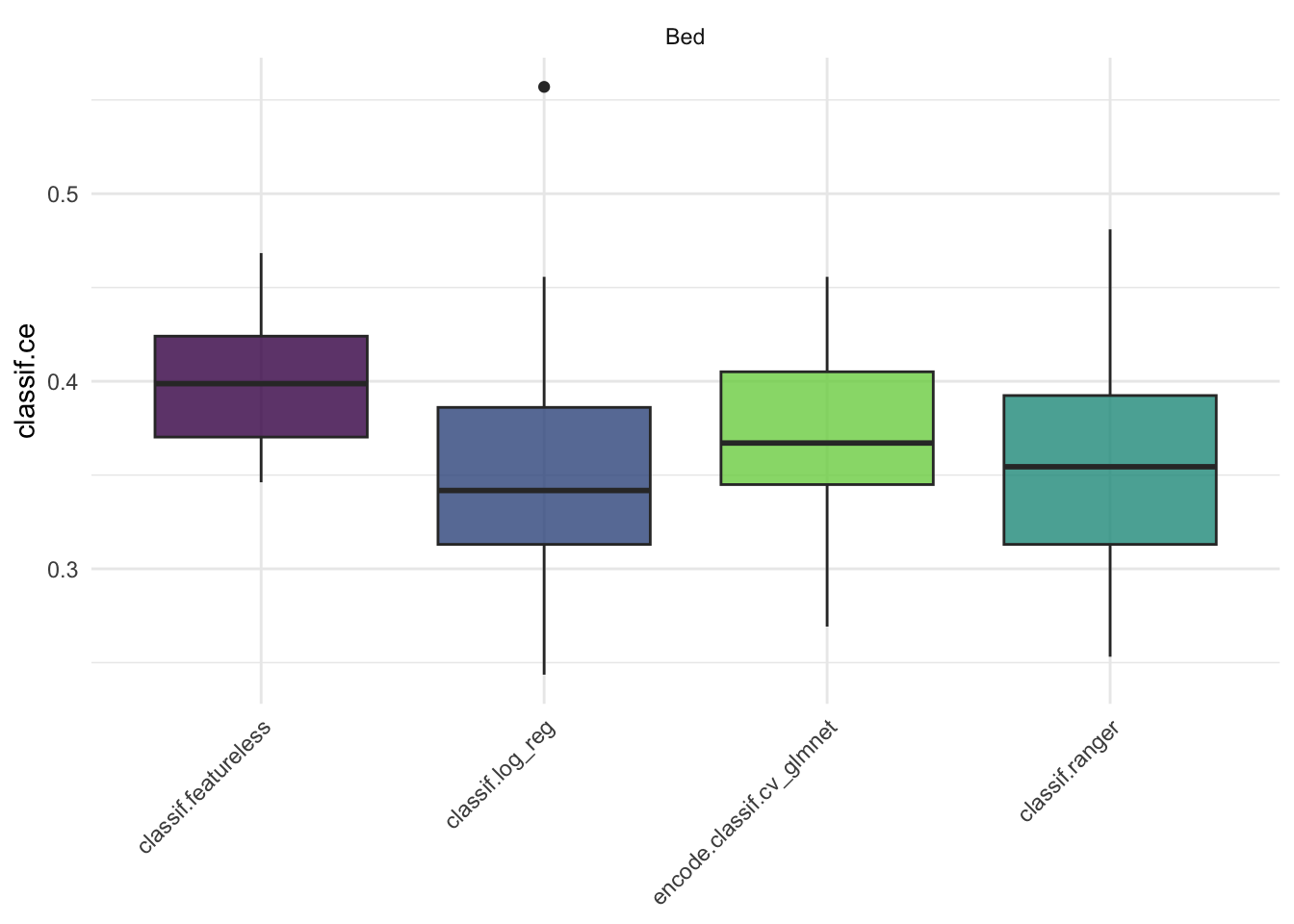
Nein, wir können nicht sicher davon ausgehen, dass alle 3 prädiktiven Modelle bezogen auf den MMCE besser funktionieren als ein Modell, das für jede Person die häufigste Klasse im Trainingsdatensatz vorhersagt. Die Box der Schätzwerte für die Performance des Featureless Learners überschneidet sich deutlich mit den Boxen der anderen 3 Modelle.
Aufgabe 2
Verwenden Sie in der Variable Bed die Ausprägung “Ja” als positive Klasse. Welche Sensitivität würden Sie ungefähr erwarten für ein Modell, dass für jede Person die häufigste Klasse im Trainingsdatensatz vorhersagt? Begründen Sie mithilfe der beobachteten Verteilung der Variable Bed im Gesamtdatensatz.
table(dat$Bed)
Ja Nein
315 473 Wenn “Ja” die positive Klasse darstellt, ist die Sensitivität definiert als der Anteil der Personen für die das Modell vorhersagt, dass sie heute ihr Bett gemacht haben, an allen Personen die heute tatsächlich ihr Bett gemacht haben. Da im Gesamtdatensatz “Nein” die häufigere Klasse ist, sollte der Featureless Learner in jedem Fold für alle Personen vorhersagen, dass die Person nicht ihr Bett gemacht hat. Da somit für keine der Personen, die tatsächlich heute ihr Bett gemacht haben der Featureless Learner eine richtige Vorhersage treffen wird, erwarten wir eine geschätzte Sensitivität des Featureless Learners von 0.
# BONUS:
# Schätze die Sensitivität des Featurelesse Learners mit mlr3
bm$aggregate(msr("classif.tpr")) nr task_id learner_id resampling_id iters classif.tpr
<int> <char> <char> <char> <int> <num>
1: 1 Bed classif.featureless cv 10 0.0000000
2: 2 Bed classif.log_reg cv 10 0.4006147
3: 3 Bed encode.classif.cv_glmnet cv 10 0.1731395
4: 4 Bed classif.ranger cv 10 0.4229339
Hidden columns: resample_resultAufgabe 3
Wenn Sie die Schätzung der erwarteten Vorhersageleistung mit unterschiedlichen Seeds wiederholen fällt auf, dass sich die Schätzwerte relativ stark unterscheiden. Wie könnte eine stabilere Schätzung der erwarteten Vorhersageleistung erreicht werden?
Eine stabilere Schätzung der erwarteten Vorhersageleistung kann mithilfe von Repeated-Cross-Validation (z.b. 10 times repeated 10-fold CV) erreicht werden.
# BONUS:
# Demonstration der Repeated CV
set.seed(1)
bm_design_2 <- benchmark_grid(
tasks = task_bed,
learners = list(fl, logreg, lasso, rf),
resamplings = rsmp("repeated_cv", repeats = 10, folds = 10)
)
bm_2 <- benchmark(bm_design_2)autoplot(bm_2, measure = msr("classif.ce"))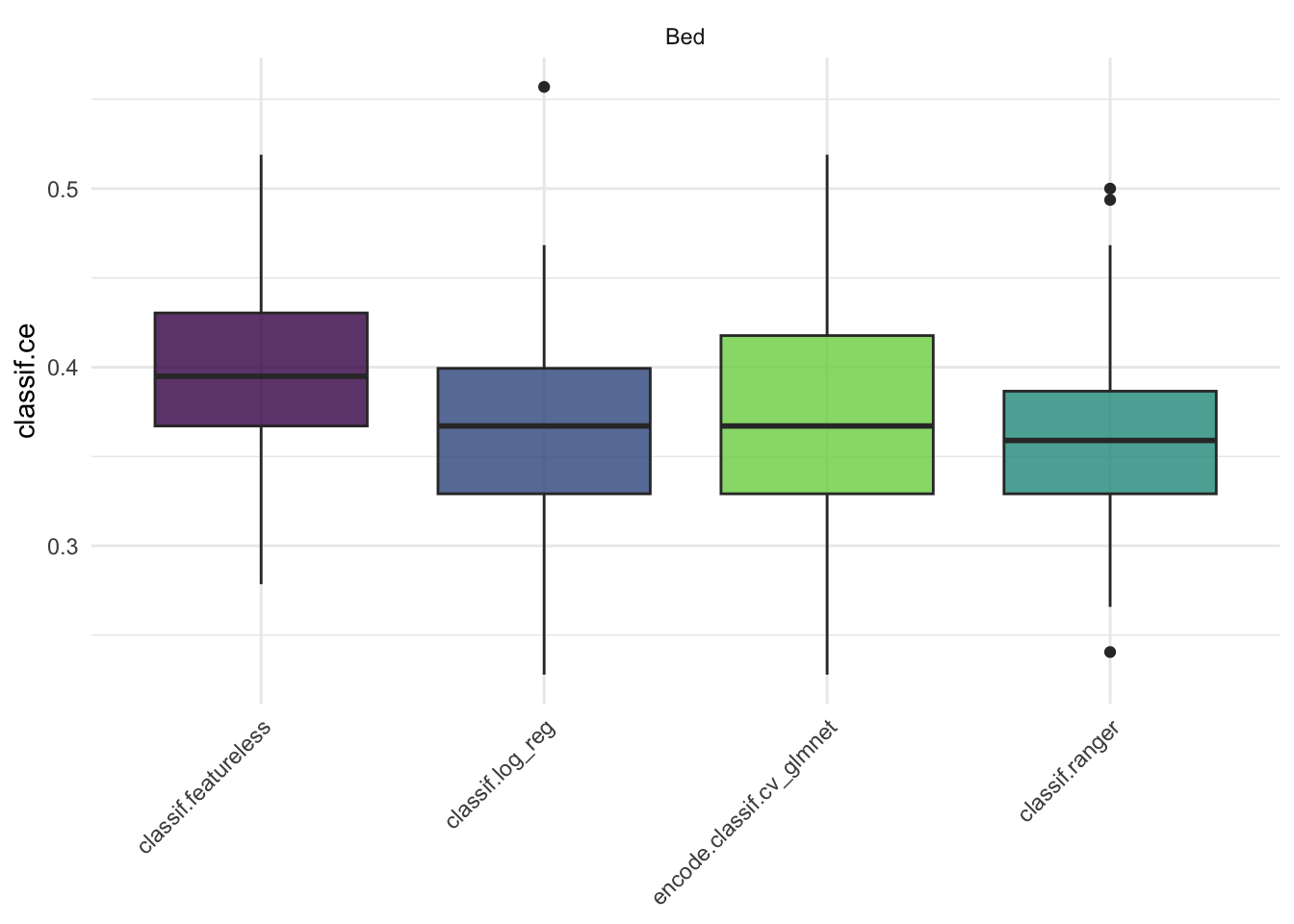
Aufgabe 4
Welches Ergebnis würden wir im Benchmark erwarten, falls zwischen den Prädiktorvariablen starke Interaktionseffekte vorliegen?
Der Random Forest ist das einzige Modell im Benchmark, dass Interaktionseffekte zwischen den Prädiktorvariablen abbilden kann. Wir würden daher erwarten, dass der Random Forest eine bessere geschätzte Vorhersageleistung im Benchmark zeigt als die logistische Regression und das LASSO, die beide (per default) keine Interaktionseffekte enthalten.
Aufgabe 5a
Betrachten Sie die Parameterschätzungen des LASSO Modells, welches Sie in der Praxis zur Vorhersage einsetzen könnten, ob eine Person heute ihr Bett gemacht hat. Verwenden Sie als Seed set.seed(2). Wie könnten Sie an den Schätzwerten erkennen, dass es sich nicht um eine normale logistische Regression handelt?
set.seed(2)
lasso$train(task_bed)
lasso_model <- lasso$model$classif.cv_glmnet$model
coef(lasso_model)19 x 1 sparse Matrix of class "dgCMatrix"
s1
(Intercept) -1.4682413
Age .
I111_a .
I141R_a .
I171_a .
I201_a .
I21R_a .
I231R_a .
I51_a .
I81R_a .
O100_a .
O10R_a .
O130R_a .
O160_a .
O190R_a .
O220R_a .
O40_a 0.4021305
O70R_a .
Sex . Der Output der Schätzwerte enthält Parameter, die exakt auf den Wert 0 (hier dargestellt als “.”) geschätzt wurden. Nur das LASSO kann durch den Regularisierungsterm eine Variablenselektion durchführen, die dazu führt dass manche Parameter komplett aus dem Modell entfernt werden (d.h. auf 0 gesetzt wurden). Bei der logistischen Regression können Schätzwerte auch nahe an 0, aber niemals exakt 0 sein.
Aufgabe 5b
Interpretieren Sie den Schätzwert des Steigungsparameters der Variable O40_a.
Die allgemeine Interpretation eines Parameters im Modell der multiple logistischen Regression bzw. LASSO (gleiche Modellgleichung) lautet an diesem Beispiel:
Für jeden Punkt mehr auf der Likert Skala des Items “Ich halte meine Sachen ordentlich und sauber.” erhöhen sich die erwarteten Log-Odds dafür heute sein Bett gemacht zu haben um 0.402, sofern die Werte auf allen anderen Prädiktoren gleich bleiben.
Da in diesem speziellen Fall das LASSO Modell jedoch alle Prädiktoren außer dem Item O40_a aus dem Modell entfernt hat, wäre auch die folgende verkürzte Interpretation korrekt:
Für jeden Punkt mehr auf der Likert Skala des Items “Ich halte meine Sachen ordentlich und sauber.” erhöhen sich die erwarteten Log-Odds dafür heute sein Bett gemacht zu haben um 0.402.
Aufgabe 5c
Berechnen Sie die geschätzte Wahrscheinlichkeit, dass eine 22 jährige Frau, die auf dem Item O40_a den Wert 4 und auf allen anderen Items den Wert 3 angegeben hat, heute morgen ihr Bett gemacht hat. Welche konkrete Vorhersage würden Sie für die Person treffen?
logistic <- function(v) {
exp(v) / (1 + exp(v))
}
logistic(-1.468 + 0.402 * 4)[1] 0.5349429# BONUS:
# Berechnung mit mlr3
newdat <- data.frame(
O10R_a = 3, O40_a = 4, O70R_a = 3, O100_a = 3, O130R_a = 3, O160_a = 3,
O190R_a = 3, O220R_a = 3,
I21R_a = 3, I51_a = 3, I81R_a = 3, I111_a = 3, I141R_a = 3, I171_a = 3,
I201_a = 3, I231R_a = 3,
Sex = "weiblich", Age = 22
)
lasso$predict_newdata(newdata = newdat)<PredictionClassif> for 1 observations:
row_ids truth response prob.Ja prob.Nein
1 <NA> Ja 0.5350128 0.4649872Die geschätzte Wahrscheinlichkeit dafür, dass eine 22 jährige Frau, die auf dem Item O40_a den Wert 4 und auf allen anderen Items den Wert 3 angegeben hat, heute morgen ihr Bett gemacht hat, beträgt 0.535. Da diese Wahrscheinlichkeit größer ist als 0.5 treffen wir die konkrete Vorhersage, dass die Person heute ihr Bett gemacht hat.
Aufgabe 5d
Angenommen es gibt in der Population Personen, die immer bei allen Fragen in Fragebögen maximal zustimmen. Wäre es bei Vorliegen dieses Phänomens zulässig, den Schätzwert des Steigungsparameter der Variable O40_a im LASSO Modell als kausalen Effekt von O40_a auf Bed zu interpretieren? Begründen Sie mithilfe der Prinzipien der kausalen Inferenz.
Bei Vorliegen dieses Phänomens wäre der Antwortstil der Personen (A_Stil) ein Counfounder des kausalen Effekts von O40_a auf Bed: O40_a <- A_Stil -> Bed. Um den kausalen Effekt von O40_a auf Bed zu schätzen, müsste für die Variable A_Stil im Modell kontrolliert werden. Da dies im aktuellen Modell nicht der Fall ist (eine solche Variable liegt im Datensatz auch gar nicht vor), kann der Schätzwert des Steigungsparameter der Variable O40_a im LASSO Modell nicht als kausaler Effekt von O40_a auf Bed interpretiert werden.