n <- 100000
x <- rnorm(n, mean = 0, sd = 1)Datensimulation, Regressionsmodelle und Kausale Inferenz mit R
1 Zufallszahlen in R
1.1 Normalverteilte Zufallszahlen
Mit der Funktion rnorm() können wir in R unabhängige normalverteilte Beobachtungen simulieren. Diese Beobachtungen sind pseudozufällig, d.h. sie haben die Eigenschaften von echten Zufallszahlen, können aber durch das setzen eines beliebigen Seeds reproduziert werden. Wenn wir den Erwartungswert und die Standardabweichung der Normalverteilung nicht explizit angeben (z.B., mean = 10, sd = 0.1), verwendet R per default die Standardnormalverteilung.
Die folgenden Beispiele veranschaulichen die Funktionsweise von rnorm():
Der Vektor x enthält 100000 zufällige, unabhängige Ziehungen aus einer Standardnormalverteilung: \[X_i \sim N(0, 1)\] Das Histogramm der Werte in x zeigt die typische “Glockenkurve”:
hist(x)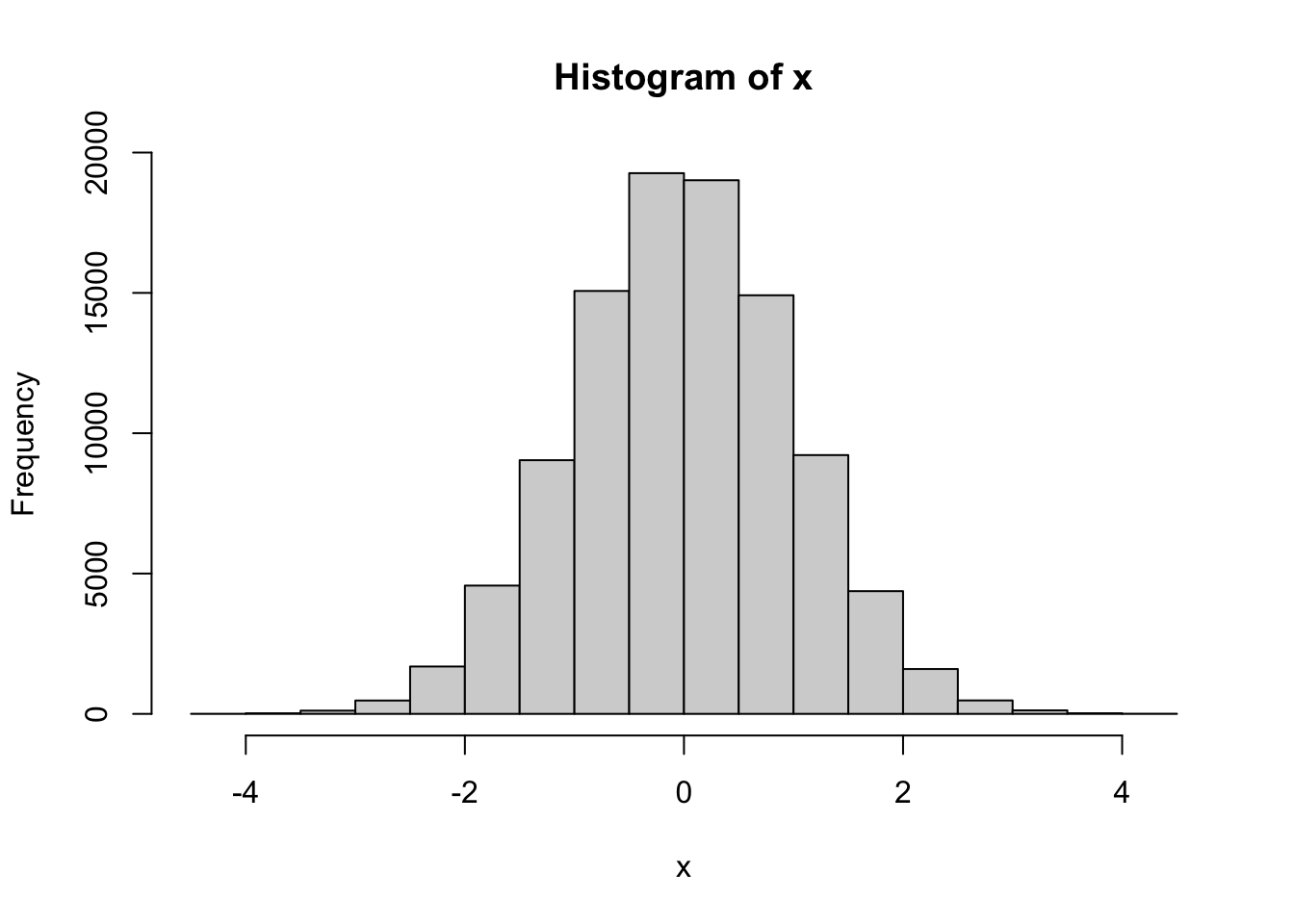
(Standard-)Normalverteilte Zufallszahlen sind kontinuierlich und können sowohl negative als auch positive Werte annehmen:
n <- 5
set.seed(42)
rnorm(n, mean = 0, sd = 1)[1] 1.3709584 -0.5646982 0.3631284 0.6328626 0.4042683Es kommen exakt die gleichen Zahlen heraus, wenn der gleiche Seed verwendet wird. Die für den Seed verwendete Zahl selbst (hier 42) hat keinerlei Bedeutung:
set.seed(42)
rnorm(n, mean = 0, sd = 1)[1] 1.3709584 -0.5646982 0.3631284 0.6328626 0.4042683Wird ein anderer Seed verwendet, kommen andere Zahlen heraus:
set.seed(3574)
rnorm(n, mean = 0, sd = 1)[1] 0.02812955 -0.26282755 0.69732108 1.50870543 -0.88743168Mit dem folgenden verkürzten Code kommen exakt die gleichen Zahlen heraus wie beim ersten Beispiel, weil der gleiche Seed verwendet wurde und rnorm wenn nicht anders angegeben per default mean = 0, sd = 1 verwendet:
set.seed(42)
rnorm(n)[1] 1.3709584 -0.5646982 0.3631284 0.6328626 0.40426831.2 Bernoulliverteilte Zufallszahlen
Mit der Funktion rbinom() können wir in R unabhängige binomialverteilte Beobachtungen simulieren. Die Bernoulliverteilung ist ein Spezialfall der Binomialverteilung mit size = 1.
Die folgenden Beispiele veranschaulichen die Funktionsweise von rbinom():
n <- 100000
x <- rbinom(n, size = 1, prob = 0.5)Der Vektor x enthält 100000 zufällige, unabhängige Ziehungen aus einer Bernoulliverteilung: \[X_i \sim B( 1, 0.5)\] Das Balkendiagramm der Werte in x zeigt, dass die Werte 0 und 1 bei \(\pi = 0.5\) ungefähr gleich häufig beobachtet werden:
barplot(table(x))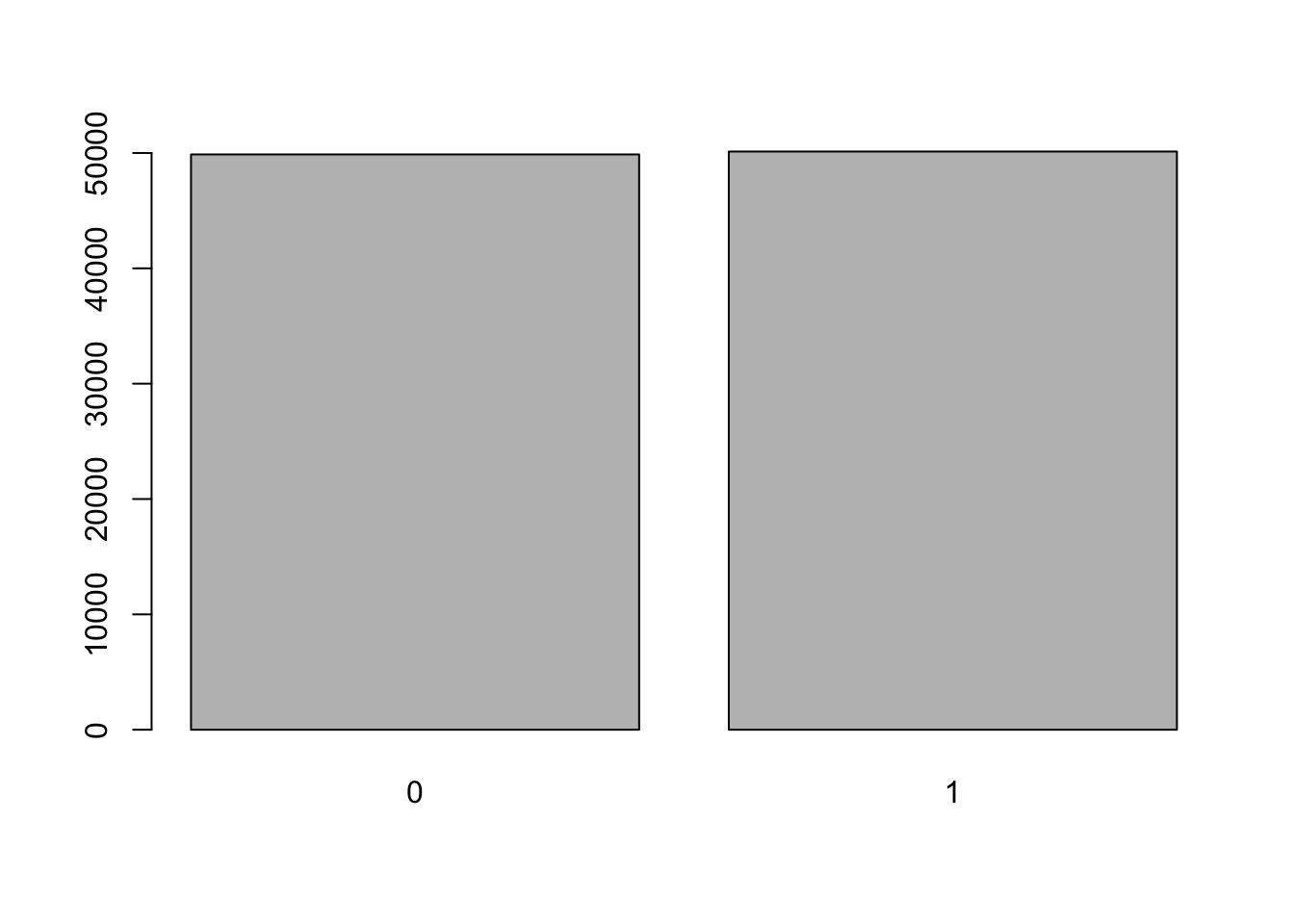
Bernoulliverteilte Zufallszahlen haben immer entweder den Wert 0 oder den Wert 1.
n <- 20
set.seed(1)
rbinom(n, size = 1, prob = 0.5) [1] 0 0 1 1 0 1 1 1 1 0 0 0 1 0 1 0 1 1 0 1Bei einer höheren Wahrscheinlichkeit für den Wert 1 (prob = 0.9), werden im Mittel auch mehr 1er beobachtet.
n <- 20
set.seed(1)
rbinom(n, size = 1, prob = 0.9) [1] 1 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 1 0 1 12 Simulation von Daten, entsprechend einem kausalen Modell
Wie simulieren wir in R Beobachtungen, sodass der Daten generierende Prozess einem bestimmten vorgegebenen kausalen Modell entspricht?
Ein sogenannter Directed Acyclic Graph (DAG), beschreibt ein heuristisches kausales Modell. Der DAG legt fest, welche Variablen sich kausal auf andere Variablen auswirken. Dabei werden noch keine Annahmen getroffen, wie die funktionale Form zwischen den Variablen genau aussieht.
Der einfachste mögliche DAG sieht folgendermaßen aus und sagt aus, dass die Variable X einen kausalen Effekt auf die Variable Y hat:

Ein kausaler Effekt bedeutet vereinfacht, dass eine Manipulation der Variable X (“Gott spielen”), eine Veränderung der Variable Y zur Folge hat (aber nicht umgekehrt).
Wenn wir Daten simulieren (und dann später auch analysieren wollen), ist es notwendig zusätzliche Annahmen über die Art der Variablen und deren Zusammenhänge zu treffen. Für die meisten einfachen Beispiele ist es ausreichend anzunehmen, dass die Variablen entweder normal- oder bernoulliverteilt sind und dass lineare (bzw. logistische) Zusammenhänge (ohne Interaktionen) zwischen den Variablen vorliegen.
In den folgenden Beispielen hat der kausale Effekt den Wert \(k = 1\).
2.1 X (normal-) und Y normalverteilt:
Dies entspricht dem Modell einer einfachen linearen Regression mit kontinuierlicher Prädiktorvariable.
n <- 100
a <- 0 # intercept
k <- 1 # slope entspricht dem kausalen Effekt
set.seed(5)
x <- rnorm(n, mean = 0, sd = 1)
y <- a + k * x + rnorm(n, mean = 0, sd = 1)
plot(x, y)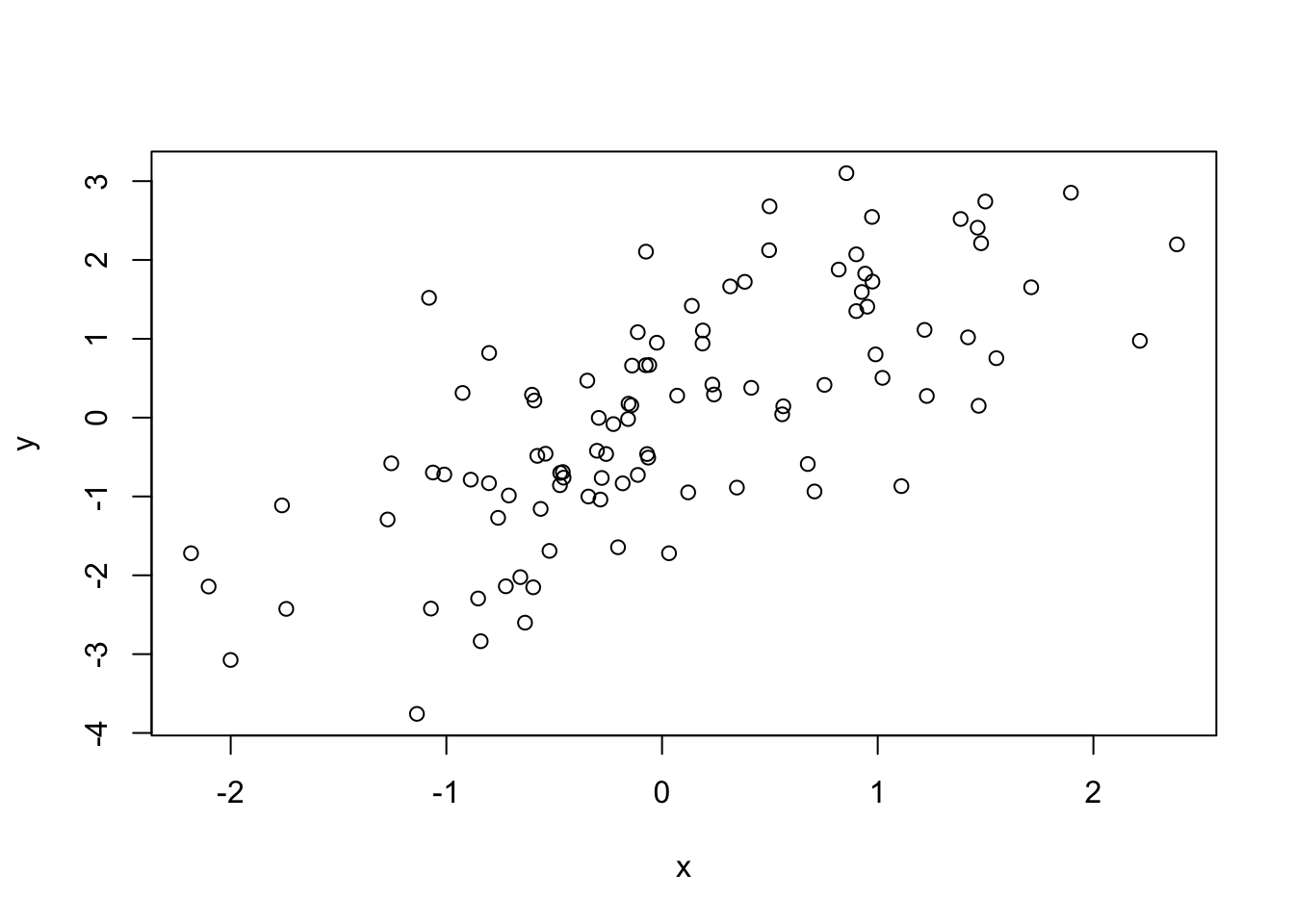
Hinweis: Der folgende verkürzte Code produziert exakt die gleichen Daten wie oben.
n <- 100
set.seed(5)
x <- rnorm(n)
y <- rnorm(n, mean = x, sd = 1)
plot(x, y)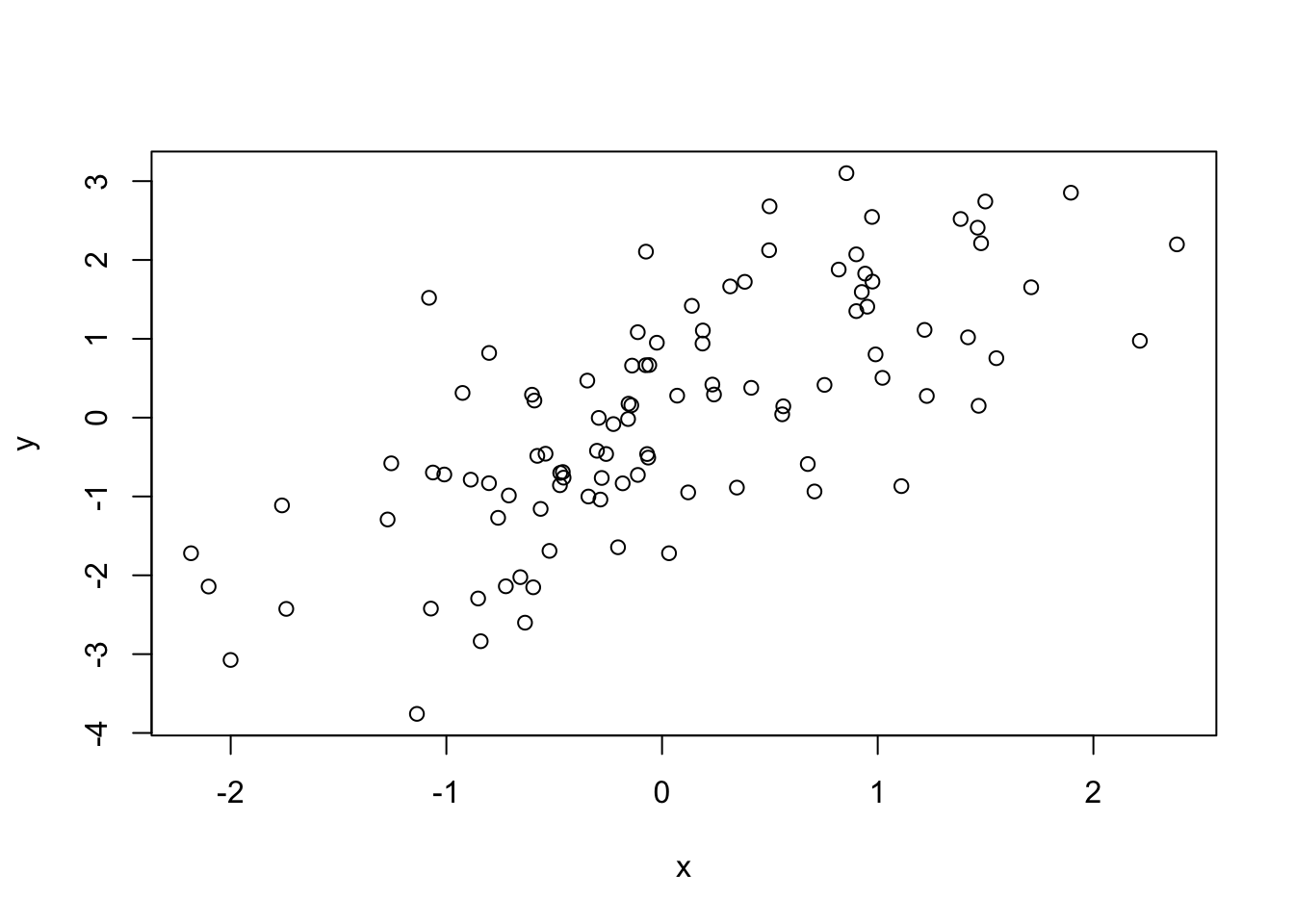
In der einfachen linearen Regression, wird die Verteilungsannahme häufig über die Verteilung der Residuen dargestellt:
\(y_i = \beta_0 + \beta_1 x_i + r_i\) mit \(r_i \sim N(0, \sigma^2_r)\)
Aufgrund einer bestimmten Eigenschaft der Normalverteilung gilt jedoch äquivalent auch:
\(y_i|x_i \sim N(\beta_0 + \beta_1 x_i, \sigma^2_r)\)
Das hat indirekt zur Folge, dass in R die beiden folgenden Schreibweisen bei der Simulation eines linearen Zusammenhangs identisch sind:
y <- 2 + 0.5 * x + rnorm(n, mean = 0, sd = 1)y <- rnorm(n, mean = 2 + 0.5 * x, sd = 1)
In unserem Tutorial werden wir ab diesem Punkt immer die 2. Schreibweise verwenden.
2.2 X (bernoulli-) und Y normalverteilt:
Dies entspricht dem Modell einer einfachen linearen Regression mit einer Dummy-Variable als Prädiktor.
n <- 100
set.seed(5)
x <- rbinom(n, size = 1, prob = 0.5)
y <- rnorm(n, mean = x, sd = 1)
boxplot(y ~ x)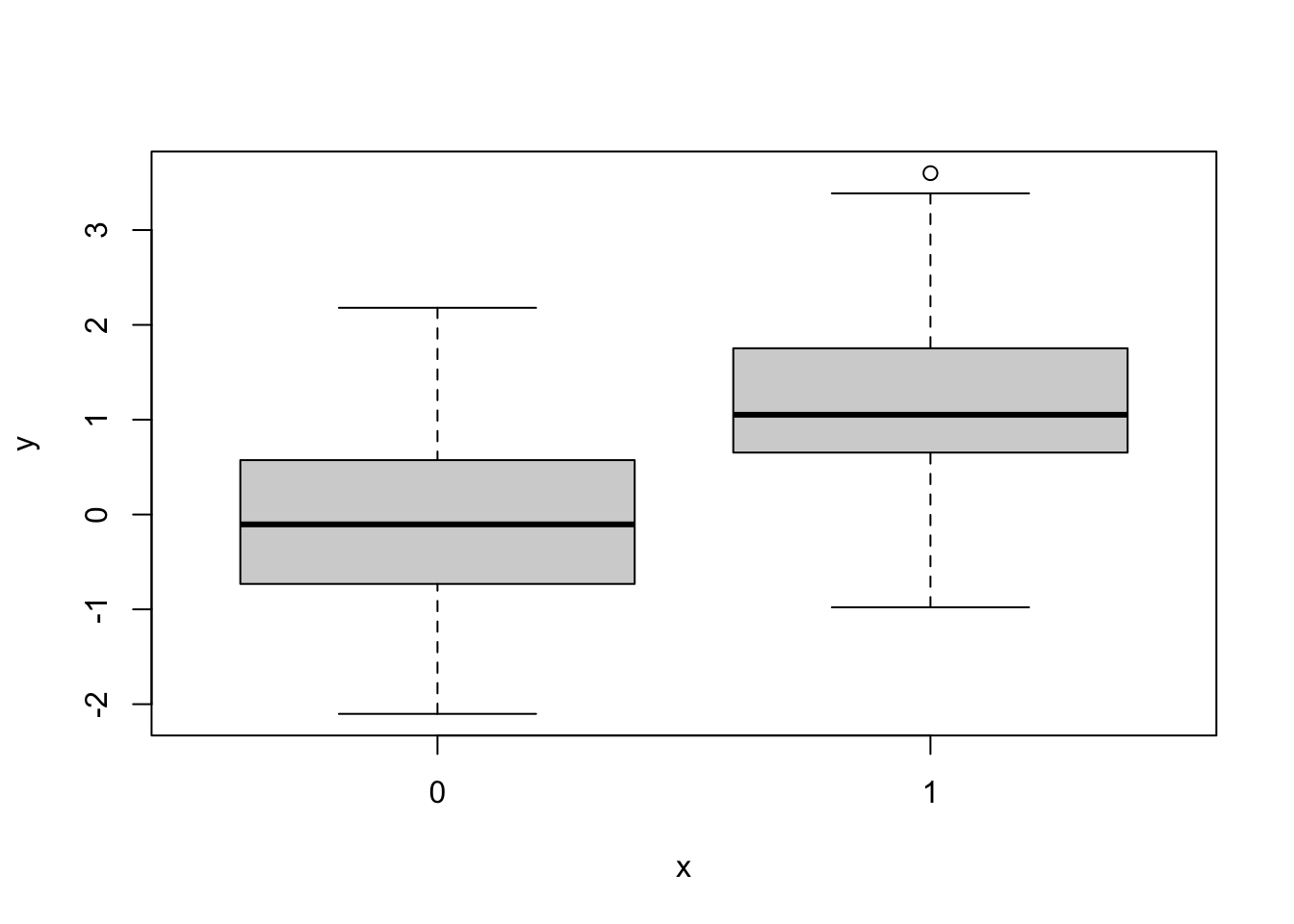
2.3 X (normal-) und Y bernoulliverteilt:
Dies entspricht dem Modell einer einfachen logistischen Regression mit kontinuierlicher Prädiktorvariable.
logistic <- function(x) {exp(x)/(1 + exp(x))}
n <- 100
set.seed(5)
x <- rnorm(n)
y <- rbinom(n, size = 1, prob = logistic(x))
plot(x, y)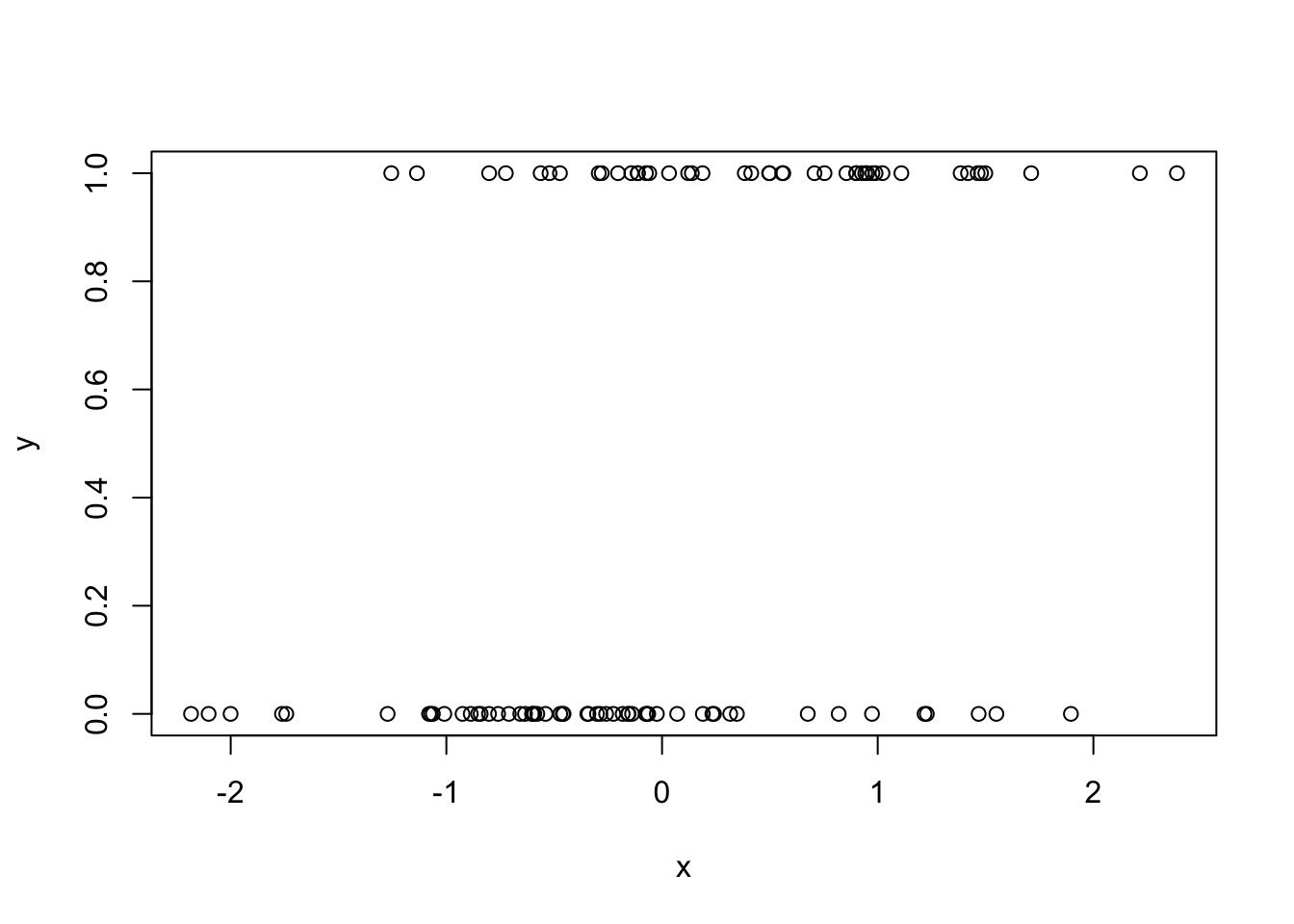
2.4 X (bernoulli-) und Y bernoulliverteilt:
Dies entspricht dem Modell einer einfachen logistischen Regression mit einer Dummy-Variable als Prädiktor.
logistic <- function(x) {exp(x)/(1 + exp(x))}
n <- 100
set.seed(5)
x <- rbinom(n, size = 1, prob = 0.5)
y <- rbinom(n, size = 1, prob = logistic(x))
table(x, y) y
x 0 1
0 31 20
1 13 363 Regressionsanalysen in R
3.1 Lineare Regression
Angenommen die normalverteilte Variable X hat einen kausalen Effekt auf die normalverteilte Variable Y, es liegt ein linearer Zusammenhang vor (und es gibt keine weiteren Variablen). Dann kann der kausale Effekt mit einer einfachen linearen Regression geschätzt werden. Die lineare Regression wird in R mithilfe der Funktion lm() berechnet.
Simulation:
Wir simulieren die Daten so, dass der kausale Effekt dem Slope \(k = 1\) entspricht.
k <- 1
n <- 1000
set.seed(3)
x <- rnorm(n)
y <- rnorm(n, mean = k * x, sd = 1)
dat <- data.frame(x = x, y = y)Analyse:
Wir berechnen eine einfache lineare Regression mit lm und betrachten die Parameterschätzung für den Slope der Variable X.
fit <- lm(y ~ x, data = dat)
summary(fit)
Call:
lm(formula = y ~ x, data = dat)
Residuals:
Min 1Q Median 3Q Max
-3.2477 -0.6699 0.0145 0.6834 3.1304
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.02047 0.03154 -0.649 0.516
x 0.97201 0.03161 30.746 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9973 on 998 degrees of freedom
Multiple R-squared: 0.4864, Adjusted R-squared: 0.4859
F-statistic: 945.3 on 1 and 998 DF, p-value: < 2.2e-16confint(fit) 2.5 % 97.5 %
(Intercept) -0.08235743 0.04141994
x 0.90997387 1.03404942Der kausale Effekt wird bei einem Schätzwert von 0.97 zuverlässig geschätzt (da wir nur eine Stichprobe zur Verfügung haben, entspricht der Schätzwert natürlich niemals exakt dem Wert 1).
3.2 Logistische Regression
Angenommen die normalverteilte Variable X hat einen kausalen Effekt auf die bernoulliverteilte Variable Y, es liegt ein logistischer Zusammenhang vor (und es gibt keine weiteren Variablen). Dann kann der kausale Effekt mithilfe einer einfachen logistischen Regression geschätzt werden. Die logistische Regression wird in R mithilfe der Funktion glm() und dem Argument family = "binomial" berechnet.
Simulation:
Wir simulieren die Daten so, dass der kausale Effekt dem Wert \(k = -1\) entspricht.
k <- -1
n <- 1000
logistic <- function(x) {exp(x) / (1 + exp(x))}
set.seed(30)
x <- rnorm(n)
y <- rbinom(n, size = 1, prob = logistic(k * x))
dat <- data.frame(x = x, y = y)Analyse:
Wir berechnen eine einfache logistische Regression mit glm und betrachten die Parameterschätzung für den Slope der Variable X.
fit <- glm(y ~ x, data = dat, family = "binomial")
summary(fit)
Call:
glm(formula = y ~ x, family = "binomial", data = dat)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.08976 0.07043 -1.274 0.202
x -1.00210 0.08048 -12.451 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1386.0 on 999 degrees of freedom
Residual deviance: 1181.1 on 998 degrees of freedom
AIC: 1185.1
Number of Fisher Scoring iterations: 3confint(fit)Waiting for profiling to be done... 2.5 % 97.5 %
(Intercept) -0.2281654 0.04805834
x -1.1636992 -0.84797737Der kausale Effekt wird bei einem Schätzwert von -1.002 zuverlässig geschätzt.
4 Wahl der richtigen Kontrollvariablen in Regressionsmodellen
Jetzt sind wir bereit für das eigentliche Thema:
Angenommen, wir kennen den DAG der dem Daten generierenden Prozess entspricht (sowie die Art der Zusammenhänge zwischen den Variablen) und das kausale Modell enthält mehr als nur zwei Variablen. Für welche Variablen sollten wir in einer linearen (oder logistischen) Regression kontrollieren, wenn wir uns für den kausalen Effekt von X auf Y interessieren?
Für welche Variablen wir kontrollieren müssen, hängt von der Struktur des DAGs, also dem Muster der kausalen Zusammenhänge ab. Bei nur drei Variablen X, Y, Z gibt es die zwei folgenden besonders wichtigen Konstellationen.
4.1 Vorliegen eines Confounders Z
DAG:
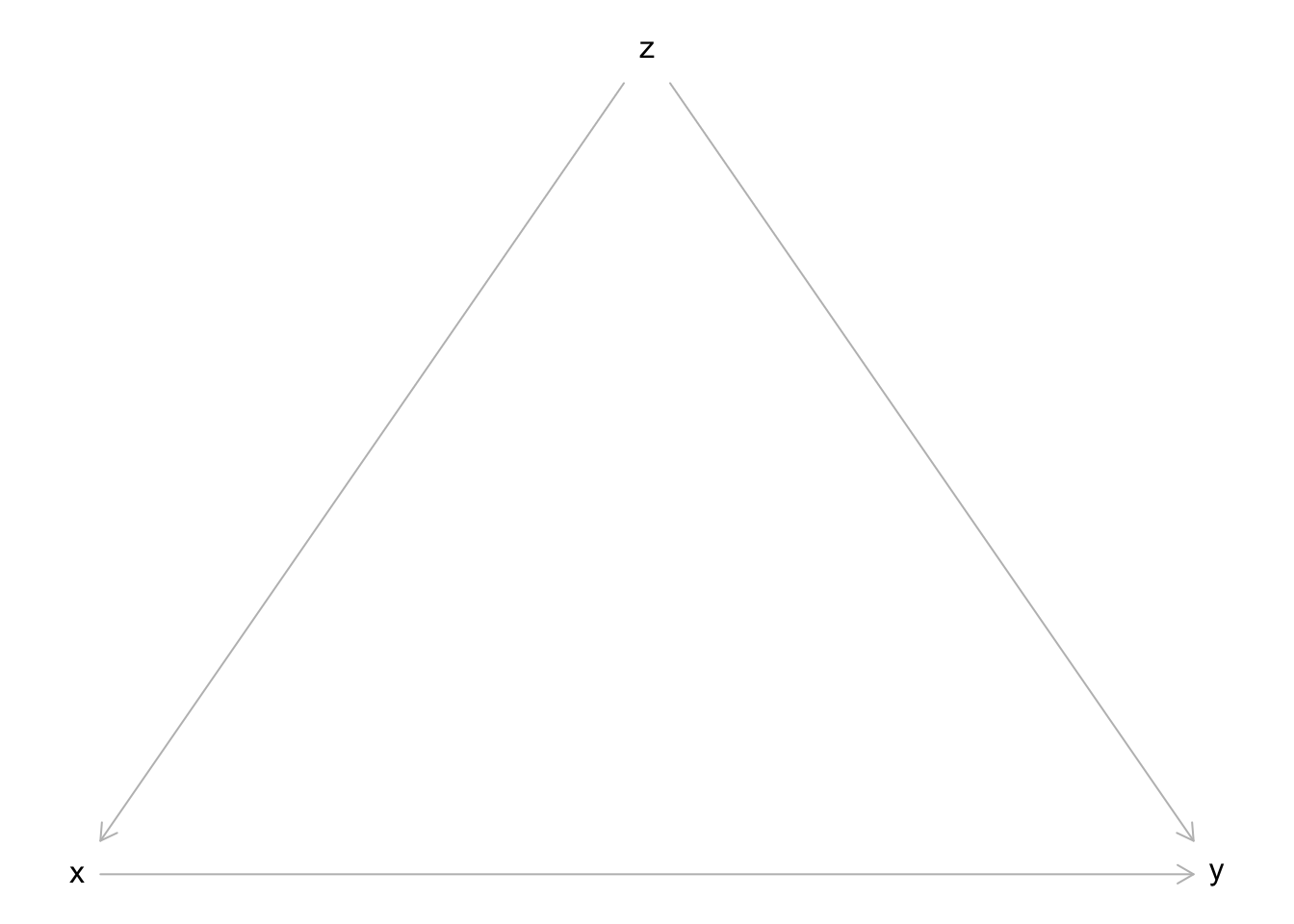
Simulation (X normal-, Y normal-, Z bernoulliverteilt):
Wir nehmen in diesem Beispiel an, dass der kausale Effekt von X auf Y dem Wert \(k = 0\) entspricht (d.h. es liegt kein kausaler Effekt vor).
k <- 0
n <- 1000
set.seed(11)
z <- rbinom(n, size = 1, prob = 0.5)
x <- rnorm(n, mean = z, sd = 1)
y <- rnorm(n, mean = k * x + z, sd = 1)
dat <- data.frame(x = x, y = y, z = z)Analyse:
Angenommen wir versuchen den kausalen Effekt von X auf Y im vorliegenden Fall mithilfe einer einfachen linearen Regression zu schätzen:
fit <- lm(y ~ x, data = dat)
summary(fit)
Call:
lm(formula = y ~ x, data = dat)
Residuals:
Min 1Q Median 3Q Max
-3.4368 -0.7092 0.0306 0.7182 3.5571
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.37067 0.03753 9.876 < 2e-16 ***
x 0.20897 0.03003 6.958 6.22e-12 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.091 on 998 degrees of freedom
Multiple R-squared: 0.04627, Adjusted R-squared: 0.04532
F-statistic: 48.42 on 1 and 998 DF, p-value: 6.224e-12confint(fit) 2.5 % 97.5 %
(Intercept) 0.2970255 0.4443235
x 0.1500384 0.2679022Wir sehen, dass der kausale Effekt mit der einfachen linearen Regression überschätzt wird: Der Schätzwert beträgt 0.21, obwohl wir durch die Simulation wissen, dass der kausale Effekt eigentlich den Wert 0 beträgt (d.h. es liegt kein kausaler Effekt vor).
Warum wird hier der kausale Effekt falsch geschätzt?
Bei der Variable Z handelt es sich hier um einen Confounder, der sich auf beide Variablen kausal auswirkt. In diesem Fall muss bei der Schätzung des kausalen Effekts von X auf Y für die Variable Z kontrolliert werden.
Wir versuchen nun, den kausalen Effekt mit einer multiplen linearen Regression zu schätzen:
fit <- lm(y ~ x + z, data = dat)
summary(fit)
Call:
lm(formula = y ~ x + z, data = dat)
Residuals:
Min 1Q Median 3Q Max
-2.90209 -0.70005 0.03392 0.67101 2.89012
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.03713 0.04366 -0.850 0.395
x -0.01069 0.03094 -0.345 0.730
z 1.05713 0.07111 14.866 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9875 on 997 degrees of freedom
Multiple R-squared: 0.2193, Adjusted R-squared: 0.2178
F-statistic: 140.1 on 2 and 997 DF, p-value: < 2.2e-16confint(fit) 2.5 % 97.5 %
(Intercept) -0.1228105 0.04855974
x -0.0714038 0.05002653
z 0.9175892 1.19666686Wie theoretisch erwartet, erhalten wir bei der Kontrolle für Z im Rahmen der multiplen linearen Regression mit einem Schätzwert von -0.01 eine sinnvolle Schätzung für den kausalen Effekt von X auf Y.
4.2 Vorliegen eines Colliders Z
DAG:
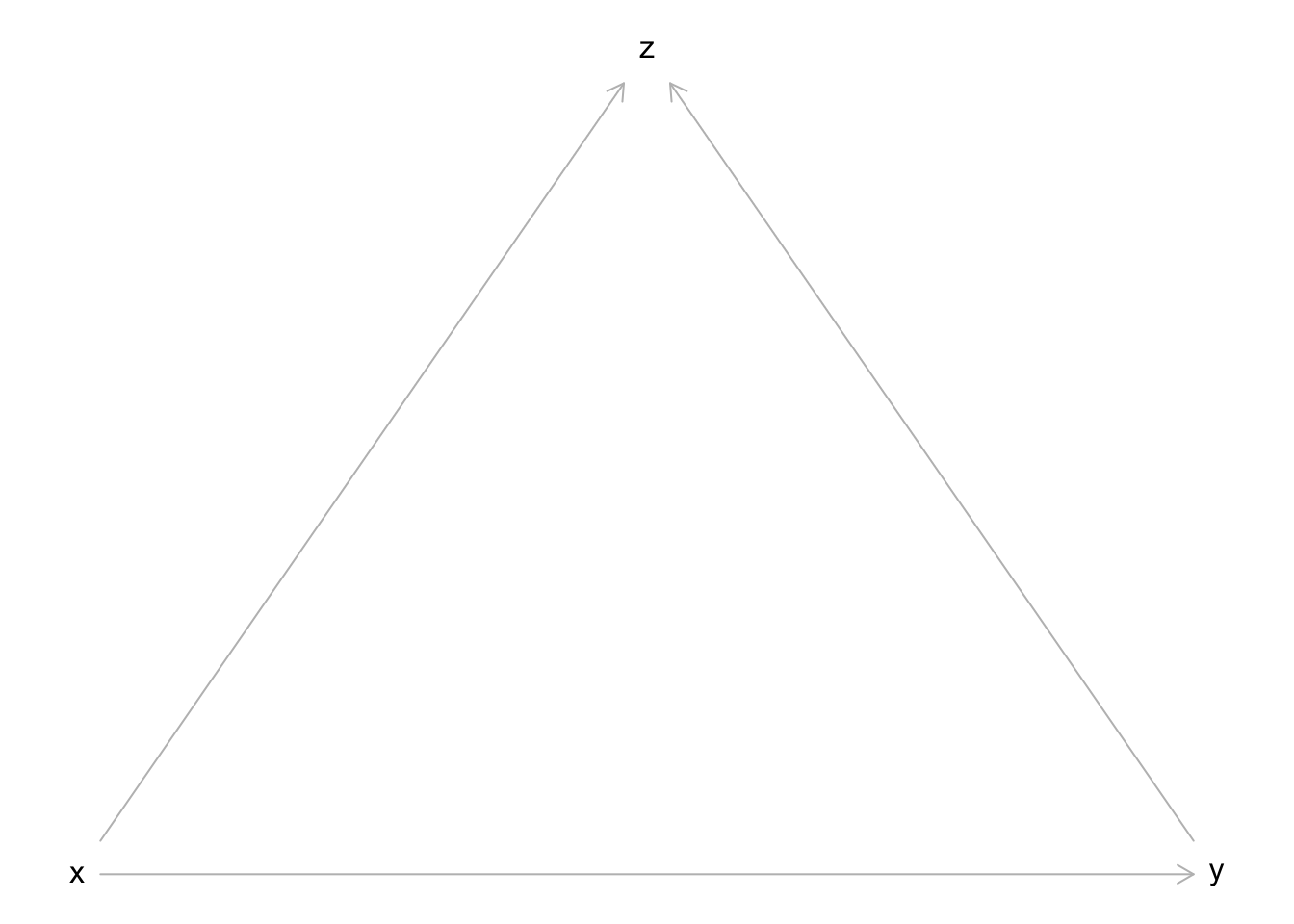
Simulation (X normal-, Y normal-, Z bernoulliverteilt):
Wir nehmen erneut an, dass der kausale Effekt von X auf Y dem Wert \(k = 0\) entspricht (d.h. es liegt kein kausaler Effekt vor).
k <- 0
n <- 1000
logistic <- function(x) {exp(x) / (1 + exp(x))}
set.seed(11)
x <- rnorm(n, mean = 0, sd = 1)
y <- rnorm(n, mean = k * x, sd = 1)
z <- rbinom(n, size = 1, prob = logistic(x + y))
dat <- data.frame(x = x, y = y, z = z)Analyse:
Bei der Variable Z handelt es sich hier um einen Collider, auf den sich sowohl X als auch Y kausal auswirken. In diesem Fall darf bei der Schätzung des kausalen Effekts von X auf Y auf keinen Fall für die Variable Z kontrolliert werden.
fit <- lm(y ~ x, data = dat)
summary(fit)
Call:
lm(formula = y ~ x, data = dat)
Residuals:
Min 1Q Median 3Q Max
-3.8620 -0.6683 0.0337 0.6594 3.1458
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.002432 0.031467 -0.077 0.938
x -0.019890 0.031601 -0.629 0.529
Residual standard error: 0.995 on 998 degrees of freedom
Multiple R-squared: 0.0003968, Adjusted R-squared: -0.0006048
F-statistic: 0.3962 on 1 and 998 DF, p-value: 0.5292confint(fit) 2.5 % 97.5 %
(Intercept) -0.06418095 0.05931651
x -0.08190137 0.04212090Die einfache lineare Regression ergibt mit einem Schätzwert von -0.02 eine sinnvolle Schätzung für den kausalen Effekt von X auf Y.
fit <- lm(y ~ x + z, data = dat)
summary(fit)
Call:
lm(formula = y ~ x + z, data = dat)
Residuals:
Min 1Q Median 3Q Max
-3.4706 -0.5994 0.0520 0.6124 2.6490
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.41884 0.04173 -10.036 < 2e-16 ***
x -0.17960 0.03119 -5.758 1.13e-08 ***
z 0.85793 0.06214 13.806 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9121 on 997 degrees of freedom
Multiple R-squared: 0.1608, Adjusted R-squared: 0.1592
F-statistic: 95.54 on 2 and 997 DF, p-value: < 2.2e-16confint(fit) 2.5 % 97.5 %
(Intercept) -0.5007348 -0.3369423
x -0.2408122 -0.1183912
z 0.7359874 0.9798663Kontrolliert man jedoch für die Variable Z im Rahmen einer multiplen linearen Regression, wird der kausale Effekt von X auf Y bei einem Schätzwert von -0.18 nicht sinnvoll geschätzt. Es liegt ein sogenannter Collider-Bias vor.
4.3 Das Backdoor Kriterium
Für die Wahl von Kontrollvariablen in komplizierteren DAGs als die elementeren Bausteine Fork, Pipe, Collider haben wir in der Vorlesung das sogenannte Backdoor Kriterium besprochen. Sehen Sie sich die Regeln dazu bitte nochmal in den Vorlesungsfolien an.
5 Übungsaufgaben
5.1 Aufgabe 1
Wiederholen Sie die Simulation aus Kapitel 4.1 für den Fall, dass X normal- , Y bernoulli- und Z normalverteilt ist. Wählen Sie \(k = 2\) und schätzen Sie den kausalen Effekt von X auf Y mithilfe einer logistischen Regression.
logistic <- function(x) {exp(x) / (1 + exp(x))}
n <- 1000
k <- 2
set.seed(11)
z <- rnorm(n)
x <- rnorm(n, mean = z, sd = 1)
y <- rbinom(n, size = 1, prob = logistic(k * x + z))
dat <- data.frame(x = x, y = y, z = z)fit <- glm(y ~ x + z, family = "binomial", data = dat)
summary(fit)
Call:
glm(formula = y ~ x + z, family = "binomial", data = dat)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.08597 0.09886 0.870 0.384
x 1.96527 0.14853 13.231 < 2e-16 ***
z 0.94047 0.15278 6.156 7.47e-10 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1385.81 on 999 degrees of freedom
Residual deviance: 647.89 on 997 degrees of freedom
AIC: 653.89
Number of Fisher Scoring iterations: 6confint(fit)Waiting for profiling to be done... 2.5 % 97.5 %
(Intercept) -0.1076265 0.2804146
x 1.6855939 2.2686490
z 0.6463455 1.2461297Die multiple logistische Regression mit den Prädiktorvariablen X und Z liefert eine sinnvolle Schätzung für den kausalen Effekt von 2.
5.2 Aufgabe 2
Es liegt der folgende DAG und eine entsprechende Datensimulation vor. Wir nehmen an, dass die Simulation dem tatsächlichen Daten generierenden Prozess einer fiktiven Studie entspricht. Die Variable U konnte bei der Studie jedoch nicht beobachtet werden (sie ist im Datensatz nicht enthalten). Schätzen Sie den kausalen Effekt von X auf Y. Bestimmen Sie die richtigen Kontrollvariablen mithilfe des in der Vorlesung behandelten “Backdoor Kriteriums”.
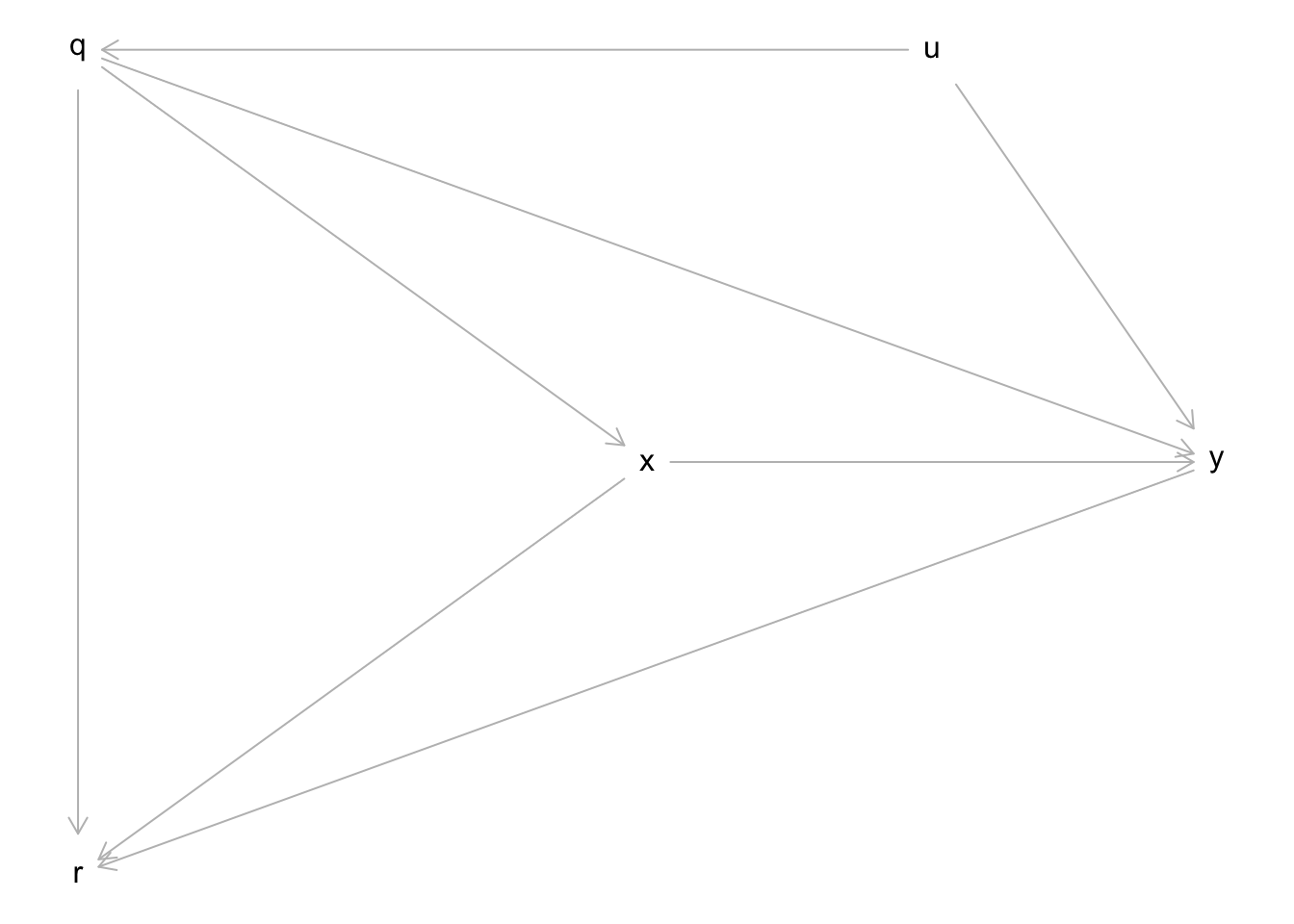
Wir setzen nun für diesen allgemeinen DAG konkrete kausale Zusammenhänge ein (wir nehmen lineare Zusammenhänge und Normalverteilungen für alle Variablen an). Die Regressionsgewichte stehen direkt vor den Prädiktoren in der jeweiligen Gleichung und werden nicht als gesonderte Variablen definiert:
n <- 10000
set.seed(95)
u <- rnorm(n)
q <- rnorm(n, mean = 1*u)
x <- rnorm(n, mean = 1*q)
y <- rnorm(n, mean = 1*u + 1*q + (-1)*x)
r <- rnorm(n, mean = 1*q + 1*x + 1*y)
dat <- data.frame(x = x, y = y, q = q, r = r)Es liegen drei Backdoor Pfade vor: 1. X <- Q <- U -> Y, 2. X <- Q -> Y, 3. X <- Q -> R <- Y. Die ersten beiden Pfade sind offen und müssen durch die Kontrolle einer Variable auf dem Pfad geschlossen werden. Beide Backdoor Pfade können durch die Kontrolle der Variable Q geschlossen werden. Der dritte Pfad ist geschlossen, denn die Variable R ist ein Collider. Für R darf daher auf keinen Fall kontrolliert werden, um den Pfad nicht versehentlich zu öffnen.
fit <- lm(y ~ x + q, data = dat)
summary(fit)
Call:
lm(formula = y ~ x + q, data = dat)
Residuals:
Min 1Q Median 3Q Max
-4.9426 -0.8266 -0.0088 0.8082 4.1961
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.02355 0.01213 -1.941 0.0523 .
x -0.99088 0.01211 -81.794 <2e-16 ***
q 1.48204 0.01481 100.078 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.213 on 9997 degrees of freedom
Multiple R-squared: 0.5005, Adjusted R-squared: 0.5004
F-statistic: 5008 on 2 and 9997 DF, p-value: < 2.2e-16confint(fit) 2.5 % 97.5 %
(Intercept) -0.04734012 0.000231849
x -1.01462661 -0.967133751
q 1.45301052 1.511067115Der kausale Effekt von X auf Y entspricht in der Simulation dem Wert -1 (siehe Regressionsgewicht von x in der Gleichung von y). Die multiple Regression mit den beiden Prädiktorvariablen X und Q liefert hierfür eine sinnvolle Schätzung.
5.3 Bonusaufgabe
In psychologischen Forschungsartikeln ist es üblich, alle Parameterschätzungen des für die Beantwortung der Forschungsfrage verwendeten Regressionsmodells gemeinsam in einer Tabelle darzustellen. Erklären Sie anhand der Ergebnisse von Aufgabe 2, welche Fehlinterpretation des Regressionsparameters der Variable Q dadurch begünstigt wird.
Der Regressionskoeffizient der Variable X entspricht im multiplen Regressionsmodell von Aufgabe 2 dem kausalen Effekt von X auf Y. Angenommen die Forschungsfrage der Studie ist es, diesen Effekt zu untersuchen. Die Variable Q muss für die Schätzung des kausalen Effekts von X auf Y als Kontrollvariable aufgenommen werden. Gleichzeitig entspricht der Regressionskoeffizient der Variable Q in diesem Modell (wenn der DAG aus Aufgabe 2 gilt) NICHT dem kausalen Effekt von Q auf Y. In der Simulation hat der kausale Effekt von Q auf Y den Wert 1. Aufgrund des Confounders U (der in der Studie nicht beobachtet wurde und daher nicht in die Regressionsanalyse als Kontrollvariable aufgenommen werden kann) liefert das Regressionsmodell aus Aufgabe 2 keine sinnvolle Schätzung für den kausalen Effekt von Q auf Y. Dadurch dass die Regressionskoeffizienten von X und Q in Ergebnistabellen üblicherweise “als gleichwertig” dargestellt werden, wird die kausale Fehlinterpretation des Regressionskoeffizients von Q begünstigt. (Hinweis: Diese Problematik ist in der Literatur auch als “Table 2 Fallacy” bekannt.)
6 Exkurs: Automatische Bestimmung von Kontrollvariablen mit dem dagitty Paket
Angenommen es liegt der folgende DAG vor:
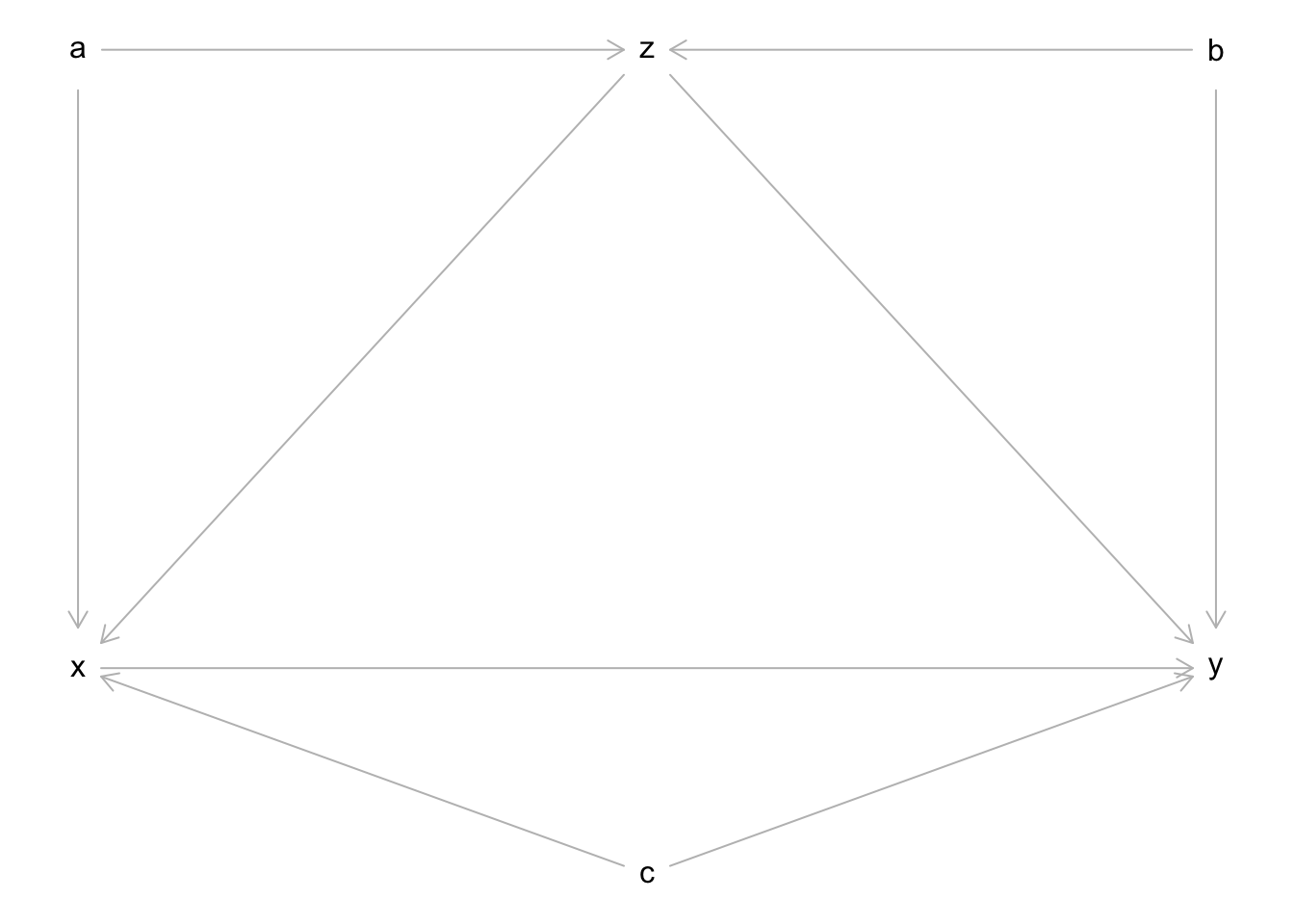
Wenn wir uns für den kausalen Effekt von X auf Y interessieren, können wir auch hier mithilfe des sogenannten Backdoor Kriteriums visuell entscheiden, für welche Variablen kontrolliert werden sollte. Wenn wir diese Regeln selbst nicht beherrschen (oder zu faul sind), können wir auch den DAG mithilfe des dagitty Pakets in R analysieren und das Paket die Kontrollvariablen nach den mathematischen Gesetzen der kausalen Inferenz automatisch bestimmen lassen.
Die folgende Syntax spezifiziert den oben abgebildeten DAG (ohne schöne Formatierung der Position der Variablen).
library(dagitty)
dag <- dagitty("dag{
x -> y
x <- z -> y
x <- c -> y
x <- a -> z
z <- b -> y
}")
plot(dag)Plot coordinates for graph not supplied! Generating coordinates, see ?coordinates for how to set your own.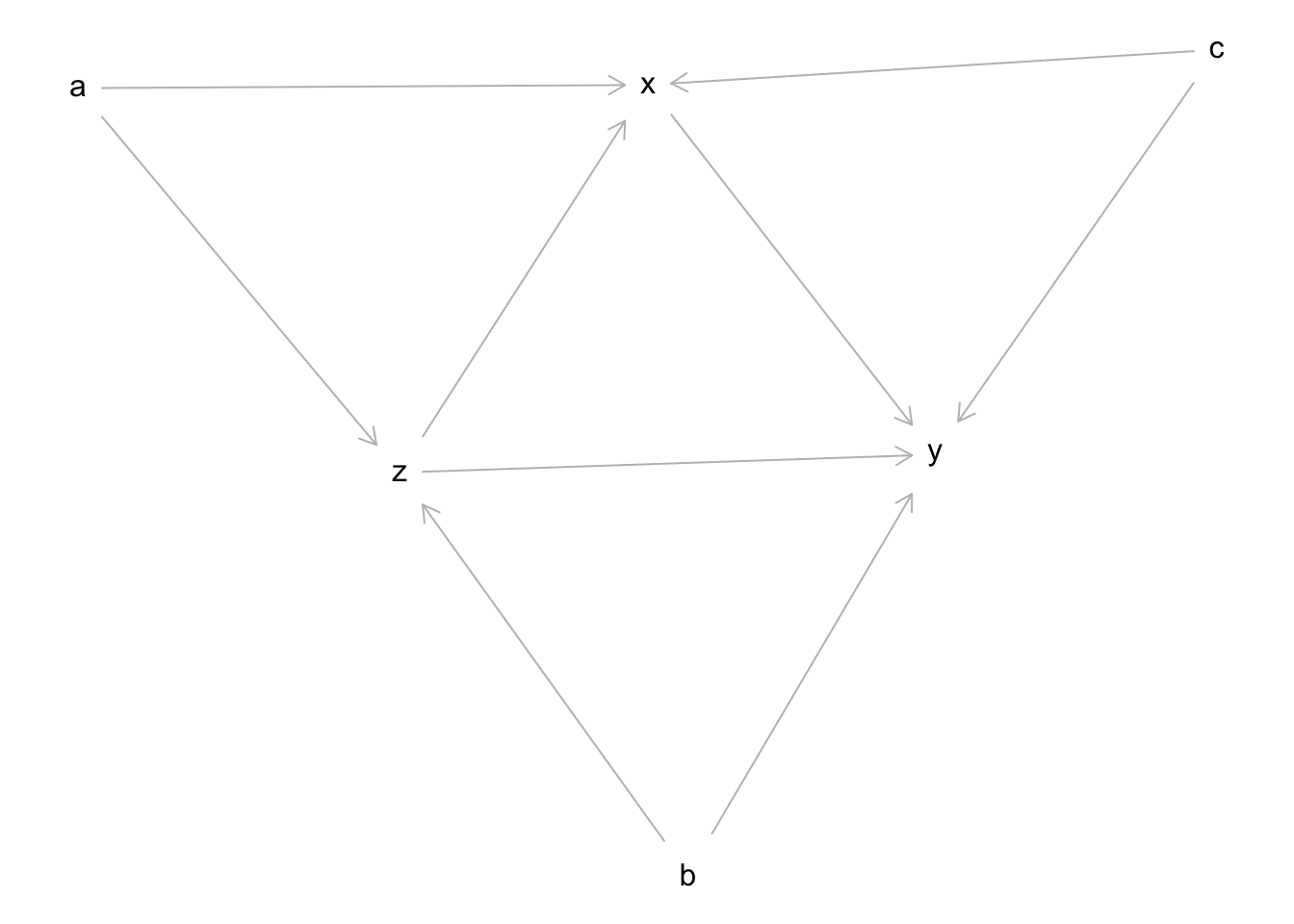
Mit der Funktion adjustmentSets() werden automatisch mögliche Mengen an Kontrollvariablen bestimmt. Dabei wird mit den Argumenten exposure, outcome und effect angegeben, welcher kausale Effekt analysiert werden soll.
adjustmentSets(dag, exposure = "x", outcome = "y", effect = "total"){ b, c, z }
{ a, c, z }Für den vorliegenden DAG gibt es zwei mögliche Mengen von Kontrollvariablen. Aus Gründen die hier nicht besprochen werden, führt die Verwendung der Kontrollvariablen B, C, Z zu einer präziseren Schätzung des kausalen Effekts und wird daher im folgenden betrachtet.
Wir demonstrieren die Schätzung des kausalen Effekts anhand der folgenden einfachen Datensimulation (alle Variablen normalverteilt). Der kausale Effekt von X auf Y entspricht hier dem Wert \(k = 2\).
n <- 1000
k <- 2
set.seed(3897)
a <- rnorm(n)
b <- rnorm(n)
c <- rnorm(n)
z <- rnorm(n, mean = a + b, sd = 1)
x <- rnorm(n, mean = a + c + z, sd = 1)
y <- rnorm(n, mean = k * x + b + c + z, sd = 1)
dat <- data.frame(a = a, b = b , c = c, x = x, y = y, z = z)Wir analysieren die simulierten Daten mit lm und verwenden die von dagitty vorgeschlagenen Variablen B, C, Z als Kontrollvariablen im Modell.
fit <- lm(y ~ x + b + c + z, data = dat)
summary(fit)
Call:
lm(formula = y ~ x + b + c + z, data = dat)
Residuals:
Min 1Q Median 3Q Max
-3.5468 -0.6660 0.0054 0.6505 2.9789
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.04054 0.03145 -1.289 0.198
x 2.00624 0.02529 79.333 <2e-16 ***
b 1.05796 0.04117 25.700 <2e-16 ***
c 0.98645 0.03970 24.846 <2e-16 ***
z 0.96436 0.04439 21.725 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9934 on 995 degrees of freedom
Multiple R-squared: 0.9841, Adjusted R-squared: 0.984
F-statistic: 1.537e+04 on 4 and 995 DF, p-value: < 2.2e-16confint(fit) 2.5 % 97.5 %
(Intercept) -0.1022631 0.02117378
x 1.9566140 2.05586532
b 0.9771796 1.13874318
c 0.9085370 1.06435520
z 0.8772544 1.05147021Die multiple lineare Regression mit den von dagitty automatisch bestimmten Kontrollvariablen ergibt mit einem Schätzwert von 2.01 eine sinnvolle Schätzung für den kausalen Effekt von X auf Y.
Während die Kontrolle für A, C, Z auch möglich gewesen wäre, führen alle anderen Kombinationen von Kontrollvariablen (inklusive der einfachen lineare Regression ohne Kontrollvariablen) allgemein nicht zum richtigen Ergebnis.