| Rennen | Platz |
|---|---|
| 1 | 5 |
| 2 | 4 |
| 3 | 1 |
| 4 | 1 |
| 5 | 1 |
| 6 | 2 |
| 7 | 3 |
| 8 | 6 |
| 9 | 4 |
| 10 | 1 |
| 11 | 3 |
| 12 | 1 |
| 13 | 4 |
| 14 | 2 |
Weitere Übungsaufgaben 2
DESKRIPTIVE STATISTIK 1: Häufigkeiten, Maßzahlen und graphische Darstellungen
Die hier veröffentlichten Übungsaufgaben sind brandneu und deshalb noch nicht auf Herz und Nieren überprüft. Sollten Sie Fehler entdecken, geben Sie uns bitte unbedingt eine Rückmeldung an philipp.sckopke(at)psy.lmu.de, damit wir so bald wie möglich eine verbesserte Version online stellen können.
Eine Sprinterin nimmt in der Saison 2023/24 an 14 Rennen teil und erzielt dabei folgende Platzierungen:
Geben Sie die absoluten und relativen Häufigkeiten, sowie die absoluten und relativen kumulierten Häufigkeiten der Platzierungen (also wie häufig der 1. Platz, der 2. Platz, usw. erzielt wurde) an.
TippLösung\(Platz\) \(H\) \(h\) \(H_{kum}\) \(h_{kum}\) 1 5 0.36 5 0.36 2 2 0.14 7 0.50 3 2 0.14 9 0.64 4 3 0.21 12 0.86 5 1 0.07 13 0.93 6 1 0.07 14 1.00 Geben Sie den Modus an.
TippLösungDer Modus der Urliste ist: 1. Platz
Eine Mathematikklausur in der 9. Klasse hat folgende Urliste ergeben:
3, 5, 1, 2, 1, 3, 5, 1, 5Berechnen Sie:
\(\sum_{i = 2}^{5}x_{i}\)
TippLösung\(\sum_{i = 2}^{5}x_{i} = 5 + 1 + 2 + 1 = 9\)
\(\sum_{i = 1}^{4}{{(x}_{i} + 2)}\)
TippLösung\(\sum_{i = 1}^{4}{{(x}_{i} + 2)} = (3 + 2) + (5 + 2) + (1 + 2) + (2 + 2) = 5+7+3+4 = 19\)
\(\sum_{i = 3}^{4}\frac{{(x_{i} + 1)}^{2}}{2}\)
TippLösung\(\sum_{i = 3}^{4}\frac{{(x_{i} + 1)}^{2}}{2} = \frac{{(1 + 1)}^{2} + {(2 + 1)}^{2}}{2} = \frac{4 + 9}{2} = \frac{13}{2} = 6.5\)
Eine Sprinterin nimmt in der Saison 2023/24 an 14 Rennen teil und erzielt dabei folgende Platzierungen:
Rennen Platz 1 5 2 3 3 5 4 6 5 5 6 4 7 5 8 5 9 4 10 3 11 4 12 6 13 6 14 1 Geben Sie die absoluten und relativen Häufigkeiten, sowie die absoluten und relativen kumulierten Häufigkeiten der Platzierungen (also wie häufig der 1. Platz, der 2. Platz, usw. erzielt wurde) an.
TippLösung\(Platz\) \(H\) \(h\) \(H_{kum}\) \(h_{kum}\) 1 1 0.07 1 0.07 2 0 0.00 1 0.07 3 2 0.14 3 0.21 4 3 0.21 6 0.43 5 5 0.36 11 0.79 6 3 0.21 14 1.00 Geben Sie den Modus an.
TippLösungDer Modus der Urliste ist: 5. Platz
Eine Mathematikklausur in der 9. Klasse hat folgende Urliste ergeben:
4, 1, 5, 2, 1, 6, 4, 1, 2Berechnen Sie:
\(\sum_{i = 2}^{5}x_{i}\)
TippLösung\(\sum_{i = 2}^{5}x_{i} = 1 + 5 + 2 + 1 = 9\)
\(\sum_{i = 1}^{4}{{(x}_{i} + 2)}\)
TippLösung\(\sum_{i = 1}^{4}{{(x}_{i} + 2)} = (4 + 2) + (1 + 2) + (5 + 2) + (2 + 2) = 6+3+7+4 = 20\)
\(\sum_{i = 3}^{4}\frac{{(x_{i} + 1)}^{2}}{2}\)
TippLösung\(\sum_{i = 3}^{4}\frac{{(x_{i} + 1)}^{2}}{2} = \frac{{(5 + 1)}^{2} + {(2 + 1)}^{2}}{2} = \frac{36 + 9}{2} = \frac{45}{2} = 22.5\)
Eine Sprinterin nimmt in der Saison 2023/24 an 14 Rennen teil und erzielt dabei folgende Platzierungen:
Rennen Platz 1 1 2 6 3 3 4 4 5 4 6 3 7 4 8 1 9 6 10 3 11 4 12 3 13 6 14 3 Geben Sie die absoluten und relativen Häufigkeiten, sowie die absoluten und relativen kumulierten Häufigkeiten der Platzierungen (also wie häufig der 1. Platz, der 2. Platz, usw. erzielt wurde) an.
TippLösung\(Platz\) \(H\) \(h\) \(H_{kum}\) \(h_{kum}\) 1 2 0.14 2 0.14 2 0 0.00 2 0.14 3 5 0.36 7 0.50 4 4 0.29 11 0.79 5 0 0.00 11 0.79 6 3 0.21 14 1.00 Geben Sie den Modus an.
TippLösungDer Modus der Urliste ist: 3. Platz
Eine Mathematikklausur in der 9. Klasse hat folgende Urliste ergeben:
2, 2, 2, 5, 3, 5, 2, 1, 3Berechnen Sie:
\(\sum_{i = 2}^{5}x_{i}\)
TippLösung\(\sum_{i = 2}^{5}x_{i} = 2 + 2 + 5 + 3 = 12\)
\(\sum_{i = 1}^{4}{{(x}_{i} + 2)}\)
TippLösung\(\sum_{i = 1}^{4}{{(x}_{i} + 2)} = (2 + 2) + (2 + 2) + (2 + 2) + (5 + 2) = 4+4+4+7 = 19\)
\(\sum_{i = 3}^{4}\frac{{(x_{i} + 1)}^{2}}{2}\)
TippLösung\(\sum_{i = 3}^{4}\frac{{(x_{i} + 1)}^{2}}{2} = \frac{{(2 + 1)}^{2} + {(5 + 1)}^{2}}{2} = \frac{9 + 36}{2} = \frac{45}{2} = 22.5\)
Eine Sprinterin nimmt in der Saison 2023/24 an 14 Rennen teil und erzielt dabei folgende Platzierungen:
Rennen Platz 1 3 2 2 3 1 4 4 5 4 6 3 7 4 8 1 9 6 10 6 11 4 12 1 13 1 14 6 Geben Sie die absoluten und relativen Häufigkeiten, sowie die absoluten und relativen kumulierten Häufigkeiten der Platzierungen (also wie häufig der 1. Platz, der 2. Platz, usw. erzielt wurde) an.
TippLösung\(Platz\) \(H\) \(h\) \(H_{kum}\) \(h_{kum}\) 1 4 0.29 4 0.29 2 1 0.07 5 0.36 3 2 0.14 7 0.50 4 4 0.29 11 0.79 5 0 0.00 11 0.79 6 3 0.21 14 1.00 Geben Sie den Modus an.
TippLösungDer Modus der Urliste ist: 1. Platz, 4. Platz
Eine Mathematikklausur in der 9. Klasse hat folgende Urliste ergeben:
4, 5, 4, 6, 6, 4, 4, 1, 2Berechnen Sie:
\(\sum_{i = 2}^{5}x_{i}\)
TippLösung\(\sum_{i = 2}^{5}x_{i} = 5 + 4 + 6 + 6 = 21\)
\(\sum_{i = 1}^{4}{{(x}_{i} + 2)}\)
TippLösung\(\sum_{i = 1}^{4}{{(x}_{i} + 2)} = (4 + 2) + (5 + 2) + (4 + 2) + (6 + 2) = 6+7+6+8 = 27\)
\(\sum_{i = 3}^{4}\frac{{(x_{i} + 1)}^{2}}{2}\)
TippLösung\(\sum_{i = 3}^{4}\frac{{(x_{i} + 1)}^{2}}{2} = \frac{{(4 + 1)}^{2} + {(6 + 1)}^{2}}{2} = \frac{25 + 49}{2} = \frac{74}{2} = 37\)
Eine Sprinterin nimmt in der Saison 2023/24 an 14 Rennen teil und erzielt dabei folgende Platzierungen:
Rennen Platz 1 4 2 1 3 5 4 6 5 3 6 1 7 6 8 4 9 2 10 5 11 1 12 2 13 2 14 2 Geben Sie die absoluten und relativen Häufigkeiten, sowie die absoluten und relativen kumulierten Häufigkeiten der Platzierungen (also wie häufig der 1. Platz, der 2. Platz, usw. erzielt wurde) an.
TippLösung\(Platz\) \(H\) \(h\) \(H_{kum}\) \(h_{kum}\) 1 3 0.21 3 0.21 2 4 0.29 7 0.50 3 1 0.07 8 0.57 4 2 0.14 10 0.71 5 2 0.14 12 0.86 6 2 0.14 14 1.00 Geben Sie den Modus an.
TippLösungDer Modus der Urliste ist: 2. Platz
Eine Mathematikklausur in der 9. Klasse hat folgende Urliste ergeben:
4, 4, 3, 4, 4, 6, 3, 4, 4Berechnen Sie:
\(\sum_{i = 2}^{5}x_{i}\)
TippLösung\(\sum_{i = 2}^{5}x_{i} = 4 + 3 + 4 + 4 = 15\)
\(\sum_{i = 1}^{4}{{(x}_{i} + 2)}\)
TippLösung\(\sum_{i = 1}^{4}{{(x}_{i} + 2)} = (4 + 2) + (4 + 2) + (3 + 2) + (4 + 2) = 6+6+5+6 = 23\)
\(\sum_{i = 3}^{4}\frac{{(x_{i} + 1)}^{2}}{2}\)
TippLösung\(\sum_{i = 3}^{4}\frac{{(x_{i} + 1)}^{2}}{2} = \frac{{(3 + 1)}^{2} + {(4 + 1)}^{2}}{2} = \frac{16 + 25}{2} = \frac{41}{2} = 20.5\)
Eine Sprinterin nimmt in der Saison 2023/24 an 14 Rennen teil und erzielt dabei folgende Platzierungen:
Rennen Platz 1 6 2 1 3 4 4 6 5 5 6 4 7 5 8 1 9 6 10 6 11 3 12 3 13 3 14 4 Geben Sie die absoluten und relativen Häufigkeiten, sowie die absoluten und relativen kumulierten Häufigkeiten der Platzierungen (also wie häufig der 1. Platz, der 2. Platz, usw. erzielt wurde) an.
TippLösung\(Platz\) \(H\) \(h\) \(H_{kum}\) \(h_{kum}\) 1 2 0.14 2 0.14 2 0 0.00 2 0.14 3 3 0.21 5 0.36 4 3 0.21 8 0.57 5 2 0.14 10 0.71 6 4 0.29 14 1.00 Geben Sie den Modus an.
TippLösungDer Modus der Urliste ist: 6. Platz
Eine Mathematikklausur in der 9. Klasse hat folgende Urliste ergeben:
3, 2, 1, 1, 5, 3, 1, 1, 5Berechnen Sie:
\(\sum_{i = 2}^{5}x_{i}\)
TippLösung\(\sum_{i = 2}^{5}x_{i} = 2 + 1 + 1 + 5 = 9\)
\(\sum_{i = 1}^{4}{{(x}_{i} + 2)}\)
TippLösung\(\sum_{i = 1}^{4}{{(x}_{i} + 2)} = (3 + 2) + (2 + 2) + (1 + 2) + (1 + 2) = 5+4+3+3 = 15\)
\(\sum_{i = 3}^{4}\frac{{(x_{i} + 1)}^{2}}{2}\)
TippLösung\(\sum_{i = 3}^{4}\frac{{(x_{i} + 1)}^{2}}{2} = \frac{{(1 + 1)}^{2} + {(1 + 1)}^{2}}{2} = \frac{4 + 4}{2} = \frac{8}{2} = 4\)
Eine Sprinterin nimmt in der Saison 2023/24 an 14 Rennen teil und erzielt dabei folgende Platzierungen:
Rennen Platz 1 3 2 4 3 3 4 3 5 3 6 3 7 4 8 4 9 5 10 6 11 4 12 4 13 4 14 6 Geben Sie die absoluten und relativen Häufigkeiten, sowie die absoluten und relativen kumulierten Häufigkeiten der Platzierungen (also wie häufig der 1. Platz, der 2. Platz, usw. erzielt wurde) an.
TippLösung\(Platz\) \(H\) \(h\) \(H_{kum}\) \(h_{kum}\) 1 0 0.00 0 0.00 2 0 0.00 0 0.00 3 5 0.36 5 0.36 4 6 0.43 11 0.79 5 1 0.07 12 0.86 6 2 0.14 14 1.00 Geben Sie den Modus an.
TippLösungDer Modus der Urliste ist: 4. Platz
Eine Mathematikklausur in der 9. Klasse hat folgende Urliste ergeben:
6, 5, 3, 6, 2, 2, 2, 3, 3Berechnen Sie:
\(\sum_{i = 2}^{5}x_{i}\)
TippLösung\(\sum_{i = 2}^{5}x_{i} = 5 + 3 + 6 + 2 = 16\)
\(\sum_{i = 1}^{4}{{(x}_{i} + 2)}\)
TippLösung\(\sum_{i = 1}^{4}{{(x}_{i} + 2)} = (6 + 2) + (5 + 2) + (3 + 2) + (6 + 2) = 8+7+5+8 = 28\)
\(\sum_{i = 3}^{4}\frac{{(x_{i} + 1)}^{2}}{2}\)
TippLösung\(\sum_{i = 3}^{4}\frac{{(x_{i} + 1)}^{2}}{2} = \frac{{(3 + 1)}^{2} + {(6 + 1)}^{2}}{2} = \frac{16 + 49}{2} = \frac{65}{2} = 32.5\)
Eine Sprinterin nimmt in der Saison 2023/24 an 14 Rennen teil und erzielt dabei folgende Platzierungen:
Rennen Platz 1 1 2 6 3 5 4 2 5 1 6 1 7 6 8 2 9 3 10 3 11 6 12 4 13 5 14 1 Geben Sie die absoluten und relativen Häufigkeiten, sowie die absoluten und relativen kumulierten Häufigkeiten der Platzierungen (also wie häufig der 1. Platz, der 2. Platz, usw. erzielt wurde) an.
TippLösung\(Platz\) \(H\) \(h\) \(H_{kum}\) \(h_{kum}\) 1 4 0.29 4 0.29 2 2 0.14 6 0.43 3 2 0.14 8 0.57 4 1 0.07 9 0.64 5 2 0.14 11 0.79 6 3 0.21 14 1.00 Geben Sie den Modus an.
TippLösungDer Modus der Urliste ist: 1. Platz
Eine Mathematikklausur in der 9. Klasse hat folgende Urliste ergeben:
6, 6, 5, 3, 1, 5, 2, 6, 5Berechnen Sie:
\(\sum_{i = 2}^{5}x_{i}\)
TippLösung\(\sum_{i = 2}^{5}x_{i} = 6 + 5 + 3 + 1 = 15\)
\(\sum_{i = 1}^{4}{{(x}_{i} + 2)}\)
TippLösung\(\sum_{i = 1}^{4}{{(x}_{i} + 2)} = (6 + 2) + (6 + 2) + (5 + 2) + (3 + 2) = 8+8+7+5 = 28\)
\(\sum_{i = 3}^{4}\frac{{(x_{i} + 1)}^{2}}{2}\)
TippLösung\(\sum_{i = 3}^{4}\frac{{(x_{i} + 1)}^{2}}{2} = \frac{{(5 + 1)}^{2} + {(3 + 1)}^{2}}{2} = \frac{36 + 16}{2} = \frac{52}{2} = 26\)
Welche Maße der zentralen Tendenz bieten sich zur Beschreibung der unten dargestellten Variablen besonders an? Begründen Sie.
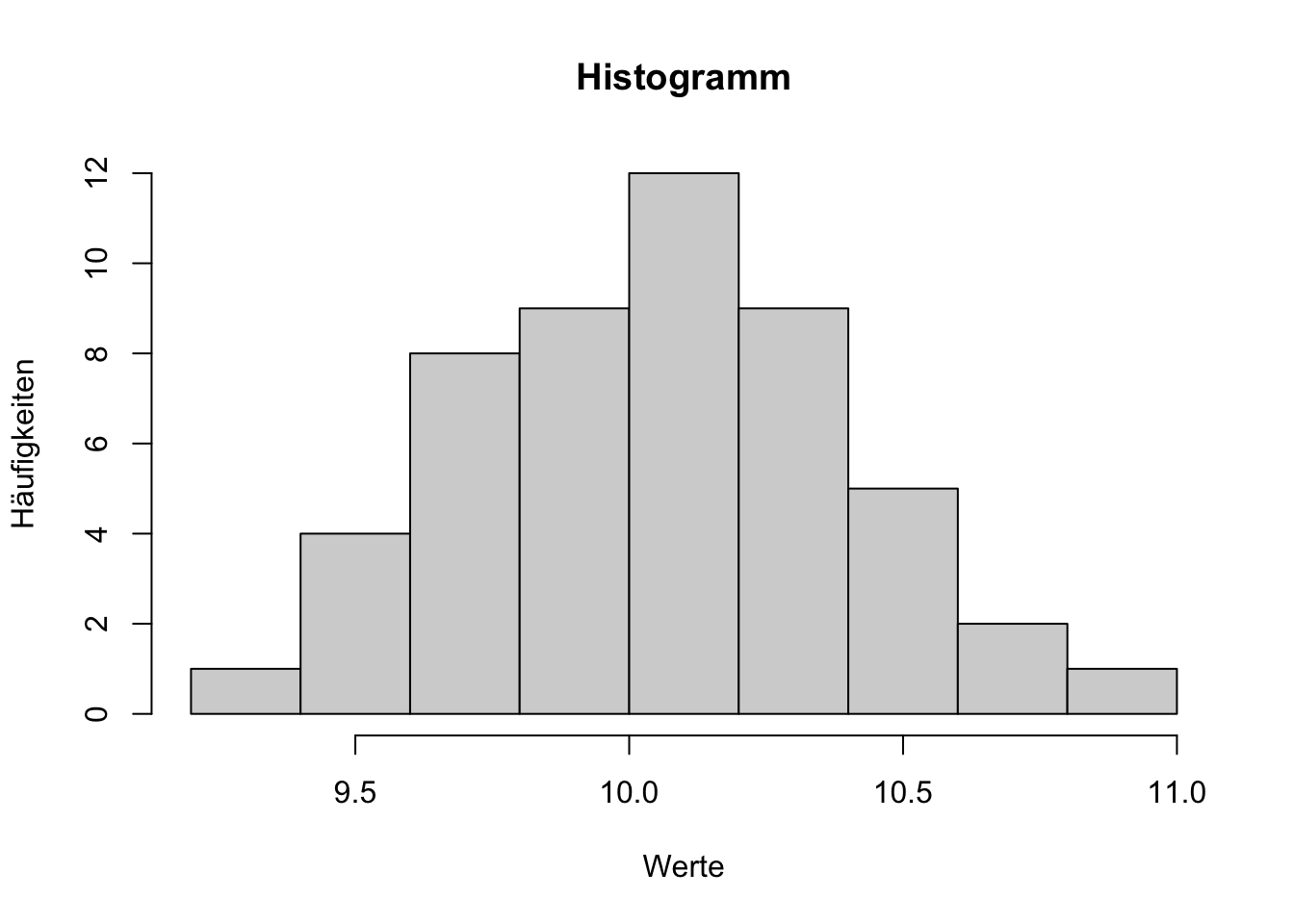
Histogramm einer Variable TippLösungEs liegen keine offensichtlichen Ausreißer vor, daher ist neben Modus und Median auch der Mittelwert ein geeignetes Maß zur Beschreibung der Daten
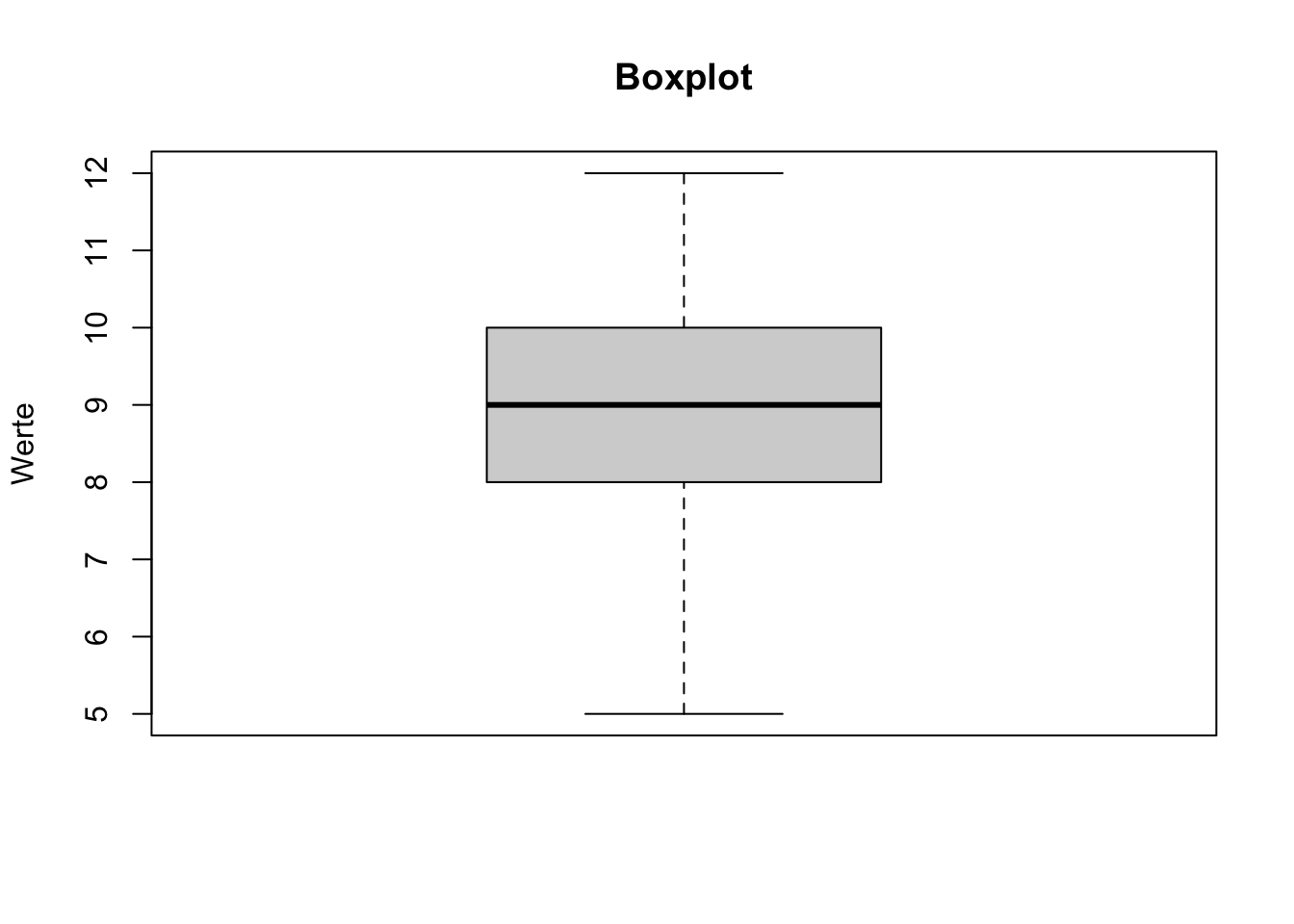
Boxplot einer anderen Variable TippLösungMittelwert, Median, Modus, wenn das Boxplot metrische Daten beschreibt. Falls nur Ordinalskalenniveau vorliegt, ist die Berechnung des Mittelwerts nicht sinnvoll. Der Median ist bereits als dicke horizontale Linie dargestellt.