| Medienkonsum in Stunden/Tag | Schlaf in Stunden | |
|---|---|---|
| Schüler 1 | 4.7 | 7.8 |
| Schüler 2 | 7.0 | 5.4 |
| Schüler 3 | 4.7 | 7.0 |
| Schüler 4 | 5.8 | 6.0 |
| Schüler 5 | 5.2 | 7.2 |
| Schüler 6 | 5.5 | 6.2 |
Weitere Übungsaufgaben 3
DESKRIPTIVE STATISTIK II: Korrelation
Die hier veröffentlichten Übungsaufgaben sind brandneu und deshalb noch nicht auf Herz und Nieren überprüft. Sollten Sie Fehler entdecken, geben Sie uns bitte unbedingt eine Rückmeldung an philipp.sckopke(at)psy.lmu.de, damit wir so bald wie möglich eine verbesserte Version online stellen können.
Ihnen liegen folgende Daten vor:
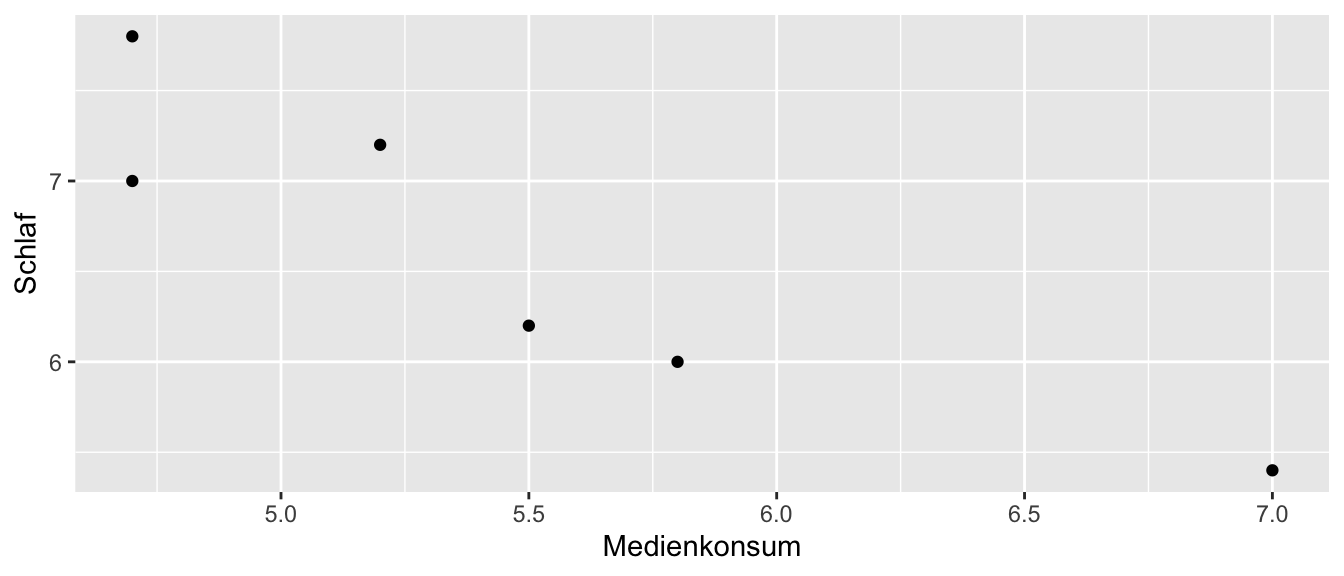
Welche Richtung hat der Zusammenhang? Drücken Sie diesen in Worten aus.
TippLösungEs liegt ein entgegengerichteter Zusammenhang vor. Je höher der tägliche Medienkonsum der Schüler ist, desto niedriger schlafen sie im Durchschnitt (bzw. umgekehrt).
Berechnen Sie die Kovarianz und interpretieren Sie diese.
TippLösung\[\bar{x} = 5.48\]
\[\bar{y} = 6.6\]
\[ \begin{align*} {cov}_{emp}(x,\ y) &= \frac{1}{n}\sum_{i = 1}^{n}\left( x_{i} - \bar{x} \right)\left( y_{i} - \bar{y} \right) \\ &= \frac{1}{6}\sum_{i = 1}^{6}\left( x_{i} - 5.48 \right)\left( y_{i} - 6.6 \right) \\ &= \frac{1}{6}\left\lbrack \left( x_{1} - 5.48 \right)\left( y_{1} - 6.6 \right) + \left( x_{2} - 5.48 \right)\left( y_{2} - 6.6 \right) + \ldots + \left( x_{5} - 5.48 \right)\left( y_{5} - 6.6 \right) \right\rbrack \\ &= \frac{1}{6}\left\lbrack (4.7 - 5.48)(7.8 - 6.6) + (7 - 5.48)(5.4 - 6.6) + \ldots + (5.5 - 5.48)(6.2 - 6.6) \right\rbrack = -0.57 \end{align*} \] Da an der Kovarianz lediglich die Richtung des Zusammenhangs abgelesen werden kann, können wir nur sagen, dass ein gegengerichteter Zusammenhang der Variablen Medienkonsum und Schlaf vorliegt.
Berechnen Sie für die beiden Variablen jeweils die Standardabweichung \(s_{emp}\).
TippLösung\[ \begin{align*} s_{emp_x} &= \sqrt{\frac{1}{n} \sum_{i = 1}^n (x_i - \bar{x})^2} \\ &= \sqrt{\frac{1}{6} [(4.7 - 5.48)^2 + (7 - 5.48)^2 + (4.7 - 5.48)^2 + (5.8 - 5.48)^2 + (5.2 - 5.48)^2 + (5.5 - 5.48)^2]} \\ &= \sqrt{\frac{1}{6} 3.72} \\ &= \sqrt{0.62} \\ &= 0.79 \\ s_{emp_y} &= \sqrt{\frac{1}{n} \sum_{i = 1}^n (y_i - \bar{y})^2} \\ &= \ ... \\ &= 0.81 \end{align*} \]
Z-standardisieren Sie beide Variablen.
TippLösung\[ z_{x_i} = \frac{x_i - \bar{x}}{\sqrt{s^2_{emp_x}}} \text{ bzw. } z_{x_i} = \frac{y_i - \bar{y}}{\sqrt{s^2_{emp_y}}} \]
Also z.B. für \(x_1 = 4.7\), \(\bar{x} = 5.48\) und \(s_{emp_x} = 0.79\):
\[ z_{x_1} = \frac{x_1 - \bar{x}}{\sqrt{s^2_{emp_x}}} = \frac{4.7 - 5.48}{0.79} \approx -0.99 \]
Medienkonsum in Stunden/Tag \(z_{Medienkonsum}\) Schlaf in Stunden \(z_{Schlaf}\) Schüler 1 4.7 -0.99 7.8 1.48 Schüler 2 7.0 1.92 5.4 -1.48 Schüler 3 4.7 -0.99 7.0 0.49 Schüler 4 5.8 0.40 6.0 -0.74 Schüler 5 5.2 -0.36 7.2 0.74 Schüler 6 5.5 0.02 6.2 -0.49 Überprüfen Sie Ihr Ergebnis auch, indem Sie den Mittelwert der \(z\)-Werte \(z_{x_i}\) bzw. \(z_{y_i}\) berechnen. Welcher Wert sollte (nach Rundung ungefähr) dabei herauskommen?
TippLösung\[\begin{align*} \bar{z}_x &= \frac{1}{6} \sum_{i = 1}^n z_{x_i} = \frac{1}{6} \cdot \lbrack (-0.99) + (1.92) + (-0.99) + (0.4) + (-0.36) + (0.02) \rbrack \approx 0 \\ \bar{z}_y &= \frac{1}{6} \sum_{i = 1}^n z_{y_i} = \frac{1}{6} \cdot \lbrack (1.48) + (-1.48) + (0.49) + (-0.74) + (0.74) + (-0.49) \rbrack \approx 0 \end{align*}\]
Berechnen Sie die Korrelation.
TippLösung\[ \begin{align*} r_{xy} &= \frac{1}{n}\sum_{i = 1}^{n}{z_{x_{i}}\cdot z_{y_{i}}} \\ &= \frac{1}{6}\sum_{i = 1}^{6}{z_{x_{i}}\cdot z_{y_{i}}} \\ &= \frac{1}{6}\left\lbrack z_{x_{1}}\cdot z_{y_{1}} + z_{x_{2}}\cdot z_{y_{2}} + \ldots + z_{x_{6}}\cdot z_{y_{6}} \right\rbrack \\ &= \frac{1}{6}\left\lbrack (-0.99)\cdot (1.48) + (1.92)\cdot (-1.48) + \ldots + ((0.02)) \cdot ((-0.49)) \right\rbrack = -0.9 \end{align*} \]
BONUS: Überprüfen Sie Ihre Ergebnisse aus allen Teilaufgaben in R.
TippLösungx <- c(4.7, 7, 4.7, 5.8, 5.2, 5.5)y <- c(7.8, 5.4, 7, 6, 7.2, 6.2)mean(x)[1] 5.483333mean(y)[1] 6.6# Kovarianz von x und y # VORSICHT! Der Befehl cov() berechnet nicht die empirische Kovarianz! # Deshalb muss die Formel hier selbst nachgebaut werden: cov_xy <- sum((x - mean(x)) * (y - mean(y))) / 6 cov_xy[1] -0.5733333# VORSICHT! Der Befehl sd() berechnet nicht die empirische Standardabweichung! # Deshalb muss die Formel hier selbst nachgebaut werden: var_x <- sum((x - mean(x))^2) / 6 sd_x <- sqrt(var_x) sd_x[1] 0.7861651var_y <- sum((y - mean(y))^2) / 6 sd_y <- sqrt(var_y) sd_y[1] 0.8082904# z-Standardisierung für x (x - mean(x)) / sd_x[1] -0.99639801 1.92919614 -0.99639801 0.40279919 -0.36039928 0.02119996# z-Standardisierung für y (y - mean(y)) / sd_y[1] 1.4846150 -1.4846150 0.4948717 -0.7423075 0.7423075 -0.4948717# Korrelation von x und y cor(x,y)[1] -0.9022482
| Medienkonsum in Stunden/Tag | Schlaf in Stunden | |
|---|---|---|
| Schüler 1 | 3.8 | 8.0 |
| Schüler 2 | 6.2 | 5.9 |
| Schüler 3 | 4.8 | 7.6 |
| Schüler 4 | 3.9 | 8.1 |
| Schüler 5 | 5.0 | 7.0 |
| Schüler 6 | 7.8 | 4.3 |
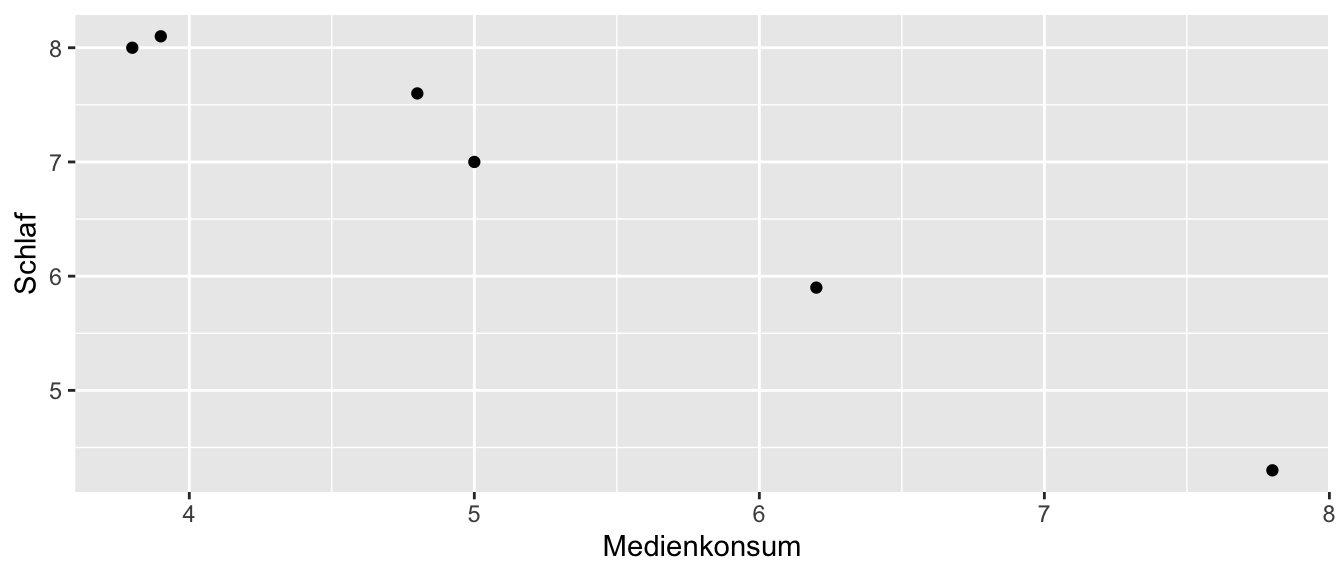
Welche Richtung hat der Zusammenhang? Drücken Sie diesen in Worten aus.
TippLösungEs liegt ein entgegengerichteter Zusammenhang vor. Je höher der tägliche Medienkonsum der Schüler ist, desto niedriger schlafen sie im Durchschnitt (bzw. umgekehrt).
Berechnen Sie die Kovarianz und interpretieren Sie diese.
TippLösung\[\bar{x} = 5.25\]
\[\bar{y} = 6.82\]
\[ \begin{align*} {cov}_{emp}(x,\ y) &= \frac{1}{n}\sum_{i = 1}^{n}\left( x_{i} - \bar{x} \right)\left( y_{i} - \bar{y} \right) \\ &= \frac{1}{6}\sum_{i = 1}^{6}\left( x_{i} - 5.25 \right)\left( y_{i} - 6.82 \right) \\ &= \frac{1}{6}\left\lbrack \left( x_{1} - 5.25 \right)\left( y_{1} - 6.82 \right) + \left( x_{2} - 5.25 \right)\left( y_{2} - 6.82 \right) + \ldots + \left( x_{5} - 5.25 \right)\left( y_{5} - 6.82 \right) \right\rbrack \\ &= \frac{1}{6}\left\lbrack (3.8 - 5.25)(8 - 6.82) + (6.2 - 5.25)(5.9 - 6.82) + \ldots + (7.8 - 5.25)(4.3 - 6.82) \right\rbrack = -1.86 \end{align*} \] Da an der Kovarianz lediglich die Richtung des Zusammenhangs abgelesen werden kann, können wir nur sagen, dass ein gegengerichteter Zusammenhang der Variablen Medienkonsum und Schlaf vorliegt.
Berechnen Sie für die beiden Variablen jeweils die Standardabweichung \(s_{emp}\).
TippLösung\[ \begin{align*} s_{emp_x} &= \sqrt{\frac{1}{n} \sum_{i = 1}^n (x_i - \bar{x})^2} \\ &= \sqrt{\frac{1}{6} [(3.8 - 5.25)^2 + (6.2 - 5.25)^2 + (4.8 - 5.25)^2 + (3.9 - 5.25)^2 + (5 - 5.25)^2 + (7.8 - 5.25)^2]} \\ &= \sqrt{\frac{1}{6} 11.58} \\ &= \sqrt{1.93} \\ &= 1.39 \\ s_{emp_y} &= \sqrt{\frac{1}{n} \sum_{i = 1}^n (y_i - \bar{y})^2} \\ &= \ ... \\ &= 1.35 \end{align*} \]
Z-standardisieren Sie beide Variablen.
TippLösung\[ z_{x_i} = \frac{x_i - \bar{x}}{\sqrt{s^2_{emp_x}}} \text{ bzw. } z_{x_i} = \frac{y_i - \bar{y}}{\sqrt{s^2_{emp_y}}} \]
Also z.B. für \(x_1 = 3.8\), \(\bar{x} = 5.25\) und \(s_{emp_x} = 1.39\):
\[ z_{x_1} = \frac{x_1 - \bar{x}}{\sqrt{s^2_{emp_x}}} = \frac{3.8 - 5.25}{1.39} \approx -1.04 \]
Medienkonsum in Stunden/Tag \(z_{Medienkonsum}\) Schlaf in Stunden \(z_{Schlaf}\) Schüler 1 3.8 -1.04 8.0 0.88 Schüler 2 6.2 0.68 5.9 -0.68 Schüler 3 4.8 -0.32 7.6 0.58 Schüler 4 3.9 -0.97 8.1 0.95 Schüler 5 5.0 -0.18 7.0 0.14 Schüler 6 7.8 1.83 4.3 -1.86 Überprüfen Sie Ihr Ergebnis auch, indem Sie den Mittelwert der \(z\)-Werte \(z_{x_i}\) bzw. \(z_{y_i}\) berechnen. Welcher Wert sollte (nach Rundung ungefähr) dabei herauskommen?
TippLösung\[\begin{align*} \bar{z}_x &= \frac{1}{6} \sum_{i = 1}^n z_{x_i} = \frac{1}{6} \cdot \lbrack (-1.04) + (0.68) + (-0.32) + (-0.97) + (-0.18) + (1.83) \rbrack \approx 0 \\ \bar{z}_y &= \frac{1}{6} \sum_{i = 1}^n z_{y_i} = \frac{1}{6} \cdot \lbrack (0.88) + (-0.68) + (0.58) + (0.95) + (0.14) + (-1.86) \rbrack \approx 0 \end{align*}\]
Berechnen Sie die Korrelation.
TippLösung\[ \begin{align*} r_{xy} &= \frac{1}{n}\sum_{i = 1}^{n}{z_{x_{i}}\cdot z_{y_{i}}} \\ &= \frac{1}{6}\sum_{i = 1}^{6}{z_{x_{i}}\cdot z_{y_{i}}} \\ &= \frac{1}{6}\left\lbrack z_{x_{1}}\cdot z_{y_{1}} + z_{x_{2}}\cdot z_{y_{2}} + \ldots + z_{x_{6}}\cdot z_{y_{6}} \right\rbrack \\ &= \frac{1}{6}\left\lbrack (-1.04)\cdot (0.88) + (0.68)\cdot (-0.68) + \ldots + ((1.83)) \cdot ((-1.86)) \right\rbrack = -0.99 \end{align*} \]
BONUS: Überprüfen Sie Ihre Ergebnisse aus allen Teilaufgaben in R.
TippLösungx <- c(3.8, 6.2, 4.8, 3.9, 5, 7.8)y <- c(8, 5.9, 7.6, 8.1, 7, 4.3)mean(x)[1] 5.25mean(y)[1] 6.816667# Kovarianz von x und y # VORSICHT! Der Befehl cov() berechnet nicht die empirische Kovarianz! # Deshalb muss die Formel hier selbst nachgebaut werden: cov_xy <- sum((x - mean(x)) * (y - mean(y))) / 6 cov_xy[1] -1.855833# VORSICHT! Der Befehl sd() berechnet nicht die empirische Standardabweichung! # Deshalb muss die Formel hier selbst nachgebaut werden: var_x <- sum((x - mean(x))^2) / 6 sd_x <- sqrt(var_x) sd_x[1] 1.390144var_y <- sum((y - mean(y))^2) / 6 sd_y <- sqrt(var_y) sd_y[1] 1.345878# z-Standardisierung für x (x - mean(x)) / sd_x[1] -1.0430575 0.6833825 -0.3237075 -0.9711225 -0.1798375 1.8343425# z-Standardisierung für y (y - mean(y)) / sd_y[1] 0.8792275 -0.6810917 0.5820238 0.9535284 0.1362183 -1.8699063# Korrelation von x und y cor(x,y)[1] -0.9919125
| Medienkonsum in Stunden/Tag | Schlaf in Stunden | |
|---|---|---|
| Schüler 1 | 5.5 | 6.7 |
| Schüler 2 | 3.9 | 7.7 |
| Schüler 3 | 4.5 | 7.0 |
| Schüler 4 | 4.9 | 7.6 |
| Schüler 5 | 6.4 | 5.7 |
| Schüler 6 | 3.7 | 8.2 |
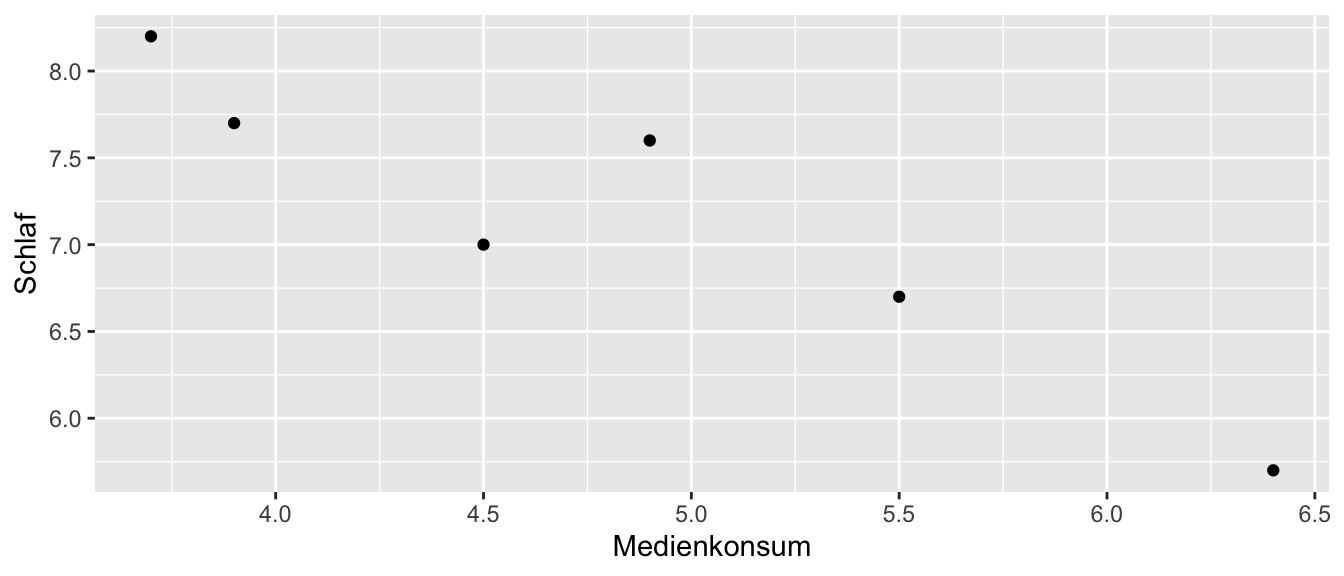
Welche Richtung hat der Zusammenhang? Drücken Sie diesen in Worten aus.
TippLösungEs liegt ein entgegengerichteter Zusammenhang vor. Je höher der tägliche Medienkonsum der Schüler ist, desto niedriger schlafen sie im Durchschnitt (bzw. umgekehrt).
Berechnen Sie die Kovarianz und interpretieren Sie diese.
TippLösung\[\bar{x} = 4.82\]
\[\bar{y} = 7.15\]
\[ \begin{align*} {cov}_{emp}(x,\ y) &= \frac{1}{n}\sum_{i = 1}^{n}\left( x_{i} - \bar{x} \right)\left( y_{i} - \bar{y} \right) \\ &= \frac{1}{6}\sum_{i = 1}^{6}\left( x_{i} - 4.82 \right)\left( y_{i} - 7.15 \right) \\ &= \frac{1}{6}\left\lbrack \left( x_{1} - 4.82 \right)\left( y_{1} - 7.15 \right) + \left( x_{2} - 4.82 \right)\left( y_{2} - 7.15 \right) + \ldots + \left( x_{5} - 4.82 \right)\left( y_{5} - 7.15 \right) \right\rbrack \\ &= \frac{1}{6}\left\lbrack (5.5 - 4.82)(6.7 - 7.15) + (3.9 - 4.82)(7.7 - 7.15) + \ldots + (3.7 - 4.82)(8.2 - 7.15) \right\rbrack = -0.7 \end{align*} \] Da an der Kovarianz lediglich die Richtung des Zusammenhangs abgelesen werden kann, können wir nur sagen, dass ein gegengerichteter Zusammenhang der Variablen Medienkonsum und Schlaf vorliegt.
Berechnen Sie für die beiden Variablen jeweils die Standardabweichung \(s_{emp}\).
TippLösung\[ \begin{align*} s_{emp_x} &= \sqrt{\frac{1}{n} \sum_{i = 1}^n (x_i - \bar{x})^2} \\ &= \sqrt{\frac{1}{6} [(5.5 - 4.82)^2 + (3.9 - 4.82)^2 + (4.5 - 4.82)^2 + (4.9 - 4.82)^2 + (6.4 - 4.82)^2 + (3.7 - 4.82)^2]} \\ &= \sqrt{\frac{1}{6} 5.16} \\ &= \sqrt{0.86} \\ &= 0.93 \\ s_{emp_y} &= \sqrt{\frac{1}{n} \sum_{i = 1}^n (y_i - \bar{y})^2} \\ &= \ ... \\ &= 0.81 \end{align*} \]
Z-standardisieren Sie beide Variablen.
TippLösung\[ z_{x_i} = \frac{x_i - \bar{x}}{\sqrt{s^2_{emp_x}}} \text{ bzw. } z_{x_i} = \frac{y_i - \bar{y}}{\sqrt{s^2_{emp_y}}} \]
Also z.B. für \(x_1 = 5.5\), \(\bar{x} = 4.82\) und \(s_{emp_x} = 0.93\):
\[ z_{x_1} = \frac{x_1 - \bar{x}}{\sqrt{s^2_{emp_x}}} = \frac{5.5 - 4.82}{0.93} \approx 0.73 \]
Medienkonsum in Stunden/Tag \(z_{Medienkonsum}\) Schlaf in Stunden \(z_{Schlaf}\) Schüler 1 5.5 0.73 6.7 -0.56 Schüler 2 3.9 -0.99 7.7 0.68 Schüler 3 4.5 -0.34 7.0 -0.19 Schüler 4 4.9 0.09 7.6 0.56 Schüler 5 6.4 1.70 5.7 -1.79 Schüler 6 3.7 -1.20 8.2 1.30 Überprüfen Sie Ihr Ergebnis auch, indem Sie den Mittelwert der \(z\)-Werte \(z_{x_i}\) bzw. \(z_{y_i}\) berechnen. Welcher Wert sollte (nach Rundung ungefähr) dabei herauskommen?
TippLösung\[\begin{align*} \bar{z}_x &= \frac{1}{6} \sum_{i = 1}^n z_{x_i} = \frac{1}{6} \cdot \lbrack (0.73) + (-0.99) + (-0.34) + (0.09) + (1.7) + (-1.2) \rbrack \approx 0 \\ \bar{z}_y &= \frac{1}{6} \sum_{i = 1}^n z_{y_i} = \frac{1}{6} \cdot \lbrack (-0.56) + (0.68) + (-0.19) + (0.56) + (-1.79) + (1.3) \rbrack \approx 0 \end{align*}\]
Berechnen Sie die Korrelation.
TippLösung\[ \begin{align*} r_{xy} &= \frac{1}{n}\sum_{i = 1}^{n}{z_{x_{i}}\cdot z_{y_{i}}} \\ &= \frac{1}{6}\sum_{i = 1}^{6}{z_{x_{i}}\cdot z_{y_{i}}} \\ &= \frac{1}{6}\left\lbrack z_{x_{1}}\cdot z_{y_{1}} + z_{x_{2}}\cdot z_{y_{2}} + \ldots + z_{x_{6}}\cdot z_{y_{6}} \right\rbrack \\ &= \frac{1}{6}\left\lbrack (0.73)\cdot (-0.56) + (-0.99)\cdot (0.68) + \ldots + ((-1.2)) \cdot ((1.3)) \right\rbrack = -0.93 \end{align*} \]
BONUS: Überprüfen Sie Ihre Ergebnisse aus allen Teilaufgaben in R.
TippLösungx <- c(5.5, 3.9, 4.5, 4.9, 6.4, 3.7)y <- c(6.7, 7.7, 7, 7.6, 5.7, 8.2)mean(x)[1] 4.816667mean(y)[1] 7.15# Kovarianz von x und y # VORSICHT! Der Befehl cov() berechnet nicht die empirische Kovarianz! # Deshalb muss die Formel hier selbst nachgebaut werden: cov_xy <- sum((x - mean(x)) * (y - mean(y))) / 6 cov_xy[1] -0.6991667# VORSICHT! Der Befehl sd() berechnet nicht die empirische Standardabweichung! # Deshalb muss die Formel hier selbst nachgebaut werden: var_x <- sum((x - mean(x))^2) / 6 sd_x <- sqrt(var_x) sd_x[1] 0.9281104var_y <- sum((y - mean(y))^2) / 6 sd_y <- sqrt(var_y) sd_y[1] 0.8098354# z-Standardisierung für x (x - mean(x)) / sd_x[1] 0.73626300 -0.98766987 -0.34119505 0.08978817 1.70597523 -1.20316148# z-Standardisierung für y (y - mean(y)) / sd_y[1] -0.5556685 0.6791504 -0.1852228 0.5556685 -1.7904874 1.2965598# Korrelation von x und y cor(x,y)[1] -0.9302171
| Medienkonsum in Stunden/Tag | Schlaf in Stunden | |
|---|---|---|
| Schüler 1 | 3.6 | 5.7 |
| Schüler 2 | 5.2 | 7.2 |
| Schüler 3 | 5.5 | 7.0 |
| Schüler 4 | 5.6 | 7.4 |
| Schüler 5 | 4.0 | 5.2 |
| Schüler 6 | 4.9 | 6.6 |
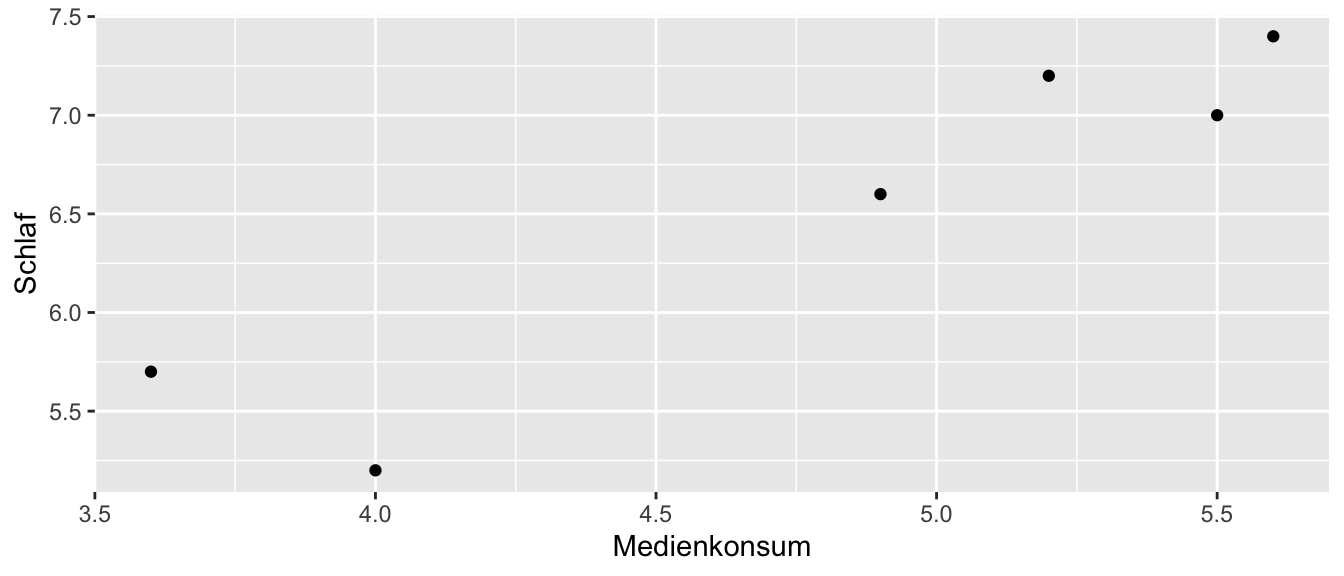
Welche Richtung hat der Zusammenhang? Drücken Sie diesen in Worten aus.
TippLösungEs liegt ein gleichgerichteter Zusammenhang vor. Je höher der tägliche Medienkonsum der Schüler ist, desto höher schlafen sie im Durchschnitt (bzw. umgekehrt).
Berechnen Sie die Kovarianz und interpretieren Sie diese.
TippLösung\[\bar{x} = 4.8\]
\[\bar{y} = 6.52\]
\[ \begin{align*} {cov}_{emp}(x,\ y) &= \frac{1}{n}\sum_{i = 1}^{n}\left( x_{i} - \bar{x} \right)\left( y_{i} - \bar{y} \right) \\ &= \frac{1}{6}\sum_{i = 1}^{6}\left( x_{i} - 4.8 \right)\left( y_{i} - 6.52 \right) \\ &= \frac{1}{6}\left\lbrack \left( x_{1} - 4.8 \right)\left( y_{1} - 6.52 \right) + \left( x_{2} - 4.8 \right)\left( y_{2} - 6.52 \right) + \ldots + \left( x_{5} - 4.8 \right)\left( y_{5} - 6.52 \right) \right\rbrack \\ &= \frac{1}{6}\left\lbrack (3.6 - 4.8)(5.7 - 6.52) + (5.2 - 4.8)(7.2 - 6.52) + \ldots + (4.9 - 4.8)(6.6 - 6.52) \right\rbrack = 0.56 \end{align*} \] Da an der Kovarianz lediglich die Richtung des Zusammenhangs abgelesen werden kann, können wir nur sagen, dass ein gleichgerichteter Zusammenhang der Variablen Medienkonsum und Schlaf vorliegt.
Berechnen Sie für die beiden Variablen jeweils die Standardabweichung \(s_{emp}\).
TippLösung\[ \begin{align*} s_{emp_x} &= \sqrt{\frac{1}{n} \sum_{i = 1}^n (x_i - \bar{x})^2} \\ &= \sqrt{\frac{1}{6} [(3.6 - 4.8)^2 + (5.2 - 4.8)^2 + (5.5 - 4.8)^2 + (5.6 - 4.8)^2 + (4 - 4.8)^2 + (4.9 - 4.8)^2]} \\ &= \sqrt{\frac{1}{6} 3.36} \\ &= \sqrt{0.56} \\ &= 0.75 \\ s_{emp_y} &= \sqrt{\frac{1}{n} \sum_{i = 1}^n (y_i - \bar{y})^2} \\ &= \ ... \\ &= 0.81 \end{align*} \]
Z-standardisieren Sie beide Variablen.
TippLösung\[ z_{x_i} = \frac{x_i - \bar{x}}{\sqrt{s^2_{emp_x}}} \text{ bzw. } z_{x_i} = \frac{y_i - \bar{y}}{\sqrt{s^2_{emp_y}}} \]
Also z.B. für \(x_1 = 3.6\), \(\bar{x} = 4.8\) und \(s_{emp_x} = 0.75\):
\[ z_{x_1} = \frac{x_1 - \bar{x}}{\sqrt{s^2_{emp_x}}} = \frac{3.6 - 4.8}{0.75} \approx -1.6 \]
Medienkonsum in Stunden/Tag \(z_{Medienkonsum}\) Schlaf in Stunden \(z_{Schlaf}\) Schüler 1 3.6 -1.60 5.7 -1.01 Schüler 2 5.2 0.53 7.2 0.84 Schüler 3 5.5 0.93 7.0 0.60 Schüler 4 5.6 1.07 7.4 1.09 Schüler 5 4.0 -1.07 5.2 -1.63 Schüler 6 4.9 0.13 6.6 0.10 Überprüfen Sie Ihr Ergebnis auch, indem Sie den Mittelwert der \(z\)-Werte \(z_{x_i}\) bzw. \(z_{y_i}\) berechnen. Welcher Wert sollte (nach Rundung ungefähr) dabei herauskommen?
TippLösung\[\begin{align*} \bar{z}_x &= \frac{1}{6} \sum_{i = 1}^n z_{x_i} = \frac{1}{6} \cdot \lbrack (-1.6) + (0.53) + (0.93) + (1.07) + (-1.07) + (0.13) \rbrack \approx 0 \\ \bar{z}_y &= \frac{1}{6} \sum_{i = 1}^n z_{y_i} = \frac{1}{6} \cdot \lbrack (-1.01) + (0.84) + (0.6) + (1.09) + (-1.63) + (0.1) \rbrack \approx 0 \end{align*}\]
Berechnen Sie die Korrelation.
TippLösung\[ \begin{align*} r_{xy} &= \frac{1}{n}\sum_{i = 1}^{n}{z_{x_{i}}\cdot z_{y_{i}}} \\ &= \frac{1}{6}\sum_{i = 1}^{6}{z_{x_{i}}\cdot z_{y_{i}}} \\ &= \frac{1}{6}\left\lbrack z_{x_{1}}\cdot z_{y_{1}} + z_{x_{2}}\cdot z_{y_{2}} + \ldots + z_{x_{6}}\cdot z_{y_{6}} \right\rbrack \\ &= \frac{1}{6}\left\lbrack (-1.6)\cdot (-1.01) + (0.53)\cdot (0.84) + \ldots + ((0.13)) \cdot ((0.1)) \right\rbrack = 0.92 \end{align*} \]
BONUS: Überprüfen Sie Ihre Ergebnisse aus allen Teilaufgaben in R.
TippLösungx <- c(3.6, 5.2, 5.5, 5.6, 4, 4.9)y <- c(5.7, 7.2, 7, 7.4, 5.2, 6.6)mean(x)[1] 4.8mean(y)[1] 6.516667# Kovarianz von x und y # VORSICHT! Der Befehl cov() berechnet nicht die empirische Kovarianz! # Deshalb muss die Formel hier selbst nachgebaut werden: cov_xy <- sum((x - mean(x)) * (y - mean(y))) / 6 cov_xy[1] 0.56# VORSICHT! Der Befehl sd() berechnet nicht die empirische Standardabweichung! # Deshalb muss die Formel hier selbst nachgebaut werden: var_x <- sum((x - mean(x))^2) / 6 sd_x <- sqrt(var_x) sd_x[1] 0.7505553var_y <- sum((y - mean(y))^2) / 6 sd_y <- sqrt(var_y) sd_y[1] 0.805019# z-Standardisierung für x (x - mean(x)) / sd_x[1] -1.5988161 0.5329387 0.9326427 1.0658774 -1.0658774 0.1332347# z-Standardisierung für y (y - mean(y)) / sd_y[1] -1.0144688 0.8488413 0.6003999 1.0972826 -1.6355722 0.1035172# Korrelation von x und y cor(x,y)[1] 0.9268281
| Medienkonsum in Stunden/Tag | Schlaf in Stunden | |
|---|---|---|
| Schüler 1 | 4.6 | 6.6 |
| Schüler 2 | 5.1 | 7.1 |
| Schüler 3 | 4.3 | 5.9 |
| Schüler 4 | 3.0 | 4.8 |
| Schüler 5 | 5.0 | 6.6 |
| Schüler 6 | 3.1 | 4.7 |
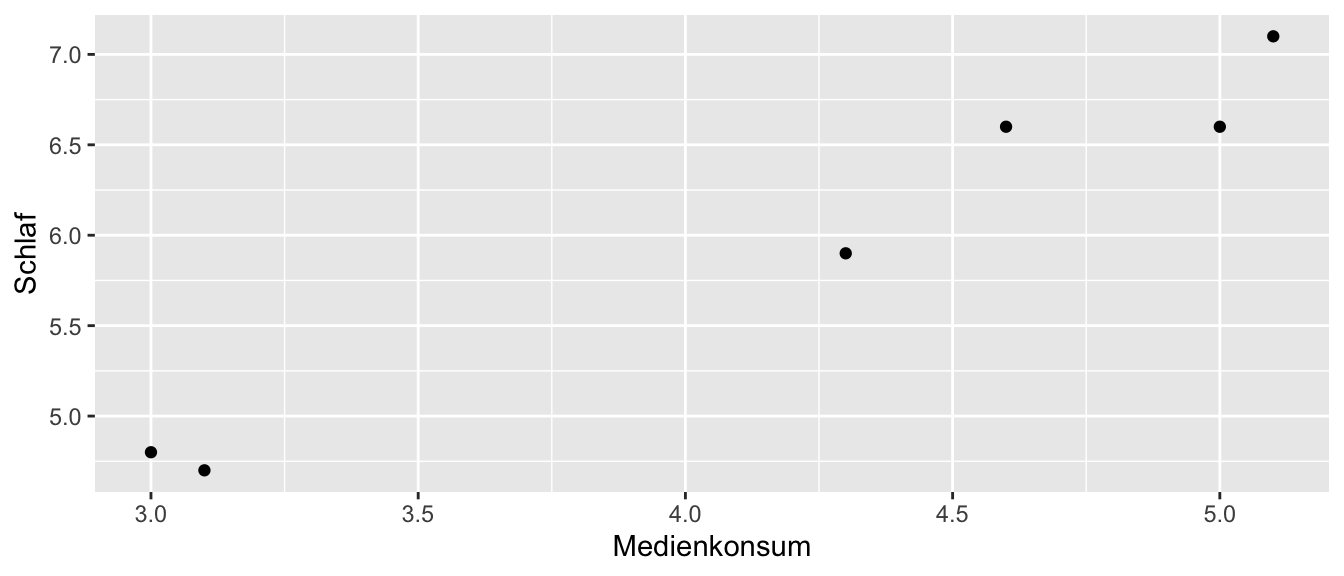
Welche Richtung hat der Zusammenhang? Drücken Sie diesen in Worten aus.
TippLösungEs liegt ein gleichgerichteter Zusammenhang vor. Je höher der tägliche Medienkonsum der Schüler ist, desto höher schlafen sie im Durchschnitt (bzw. umgekehrt).
Berechnen Sie die Kovarianz und interpretieren Sie diese.
TippLösung\[\bar{x} = 4.18\]
\[\bar{y} = 5.95\]
\[ \begin{align*} {cov}_{emp}(x,\ y) &= \frac{1}{n}\sum_{i = 1}^{n}\left( x_{i} - \bar{x} \right)\left( y_{i} - \bar{y} \right) \\ &= \frac{1}{6}\sum_{i = 1}^{6}\left( x_{i} - 4.18 \right)\left( y_{i} - 5.95 \right) \\ &= \frac{1}{6}\left\lbrack \left( x_{1} - 4.18 \right)\left( y_{1} - 5.95 \right) + \left( x_{2} - 4.18 \right)\left( y_{2} - 5.95 \right) + \ldots + \left( x_{5} - 4.18 \right)\left( y_{5} - 5.95 \right) \right\rbrack \\ &= \frac{1}{6}\left\lbrack (4.6 - 4.18)(6.6 - 5.95) + (5.1 - 4.18)(7.1 - 5.95) + \ldots + (3.1 - 4.18)(4.7 - 5.95) \right\rbrack = 0.76 \end{align*} \] Da an der Kovarianz lediglich die Richtung des Zusammenhangs abgelesen werden kann, können wir nur sagen, dass ein gleichgerichteter Zusammenhang der Variablen Medienkonsum und Schlaf vorliegt.
Berechnen Sie für die beiden Variablen jeweils die Standardabweichung \(s_{emp}\).
TippLösung\[ \begin{align*} s_{emp_x} &= \sqrt{\frac{1}{n} \sum_{i = 1}^n (x_i - \bar{x})^2} \\ &= \sqrt{\frac{1}{6} [(4.6 - 4.18)^2 + (5.1 - 4.18)^2 + (4.3 - 4.18)^2 + (3 - 4.18)^2 + (5 - 4.18)^2 + (3.1 - 4.18)^2]} \\ &= \sqrt{\frac{1}{6} 4.26} \\ &= \sqrt{0.71} \\ &= 0.84 \\ s_{emp_y} &= \sqrt{\frac{1}{n} \sum_{i = 1}^n (y_i - \bar{y})^2} \\ &= \ ... \\ &= 0.92 \end{align*} \]
Z-standardisieren Sie beide Variablen.
TippLösung\[ z_{x_i} = \frac{x_i - \bar{x}}{\sqrt{s^2_{emp_x}}} \text{ bzw. } z_{x_i} = \frac{y_i - \bar{y}}{\sqrt{s^2_{emp_y}}} \]
Also z.B. für \(x_1 = 4.6\), \(\bar{x} = 4.18\) und \(s_{emp_x} = 0.84\):
\[ z_{x_1} = \frac{x_1 - \bar{x}}{\sqrt{s^2_{emp_x}}} = \frac{4.6 - 4.18}{0.84} \approx 0.5 \]
Medienkonsum in Stunden/Tag \(z_{Medienkonsum}\) Schlaf in Stunden \(z_{Schlaf}\) Schüler 1 4.6 0.50 6.6 0.71 Schüler 2 5.1 1.09 7.1 1.25 Schüler 3 4.3 0.14 5.9 -0.05 Schüler 4 3.0 -1.41 4.8 -1.25 Schüler 5 5.0 0.97 6.6 0.71 Schüler 6 3.1 -1.29 4.7 -1.36 Überprüfen Sie Ihr Ergebnis auch, indem Sie den Mittelwert der \(z\)-Werte \(z_{x_i}\) bzw. \(z_{y_i}\) berechnen. Welcher Wert sollte (nach Rundung ungefähr) dabei herauskommen?
TippLösung\[\begin{align*} \bar{z}_x &= \frac{1}{6} \sum_{i = 1}^n z_{x_i} = \frac{1}{6} \cdot \lbrack (0.5) + (1.09) + (0.14) + (-1.41) + (0.97) + (-1.29) \rbrack \approx 0 \\ \bar{z}_y &= \frac{1}{6} \sum_{i = 1}^n z_{y_i} = \frac{1}{6} \cdot \lbrack (0.71) + (1.25) + (-0.05) + (-1.25) + (0.71) + (-1.36) \rbrack \approx 0 \end{align*}\]
Berechnen Sie die Korrelation.
TippLösung\[ \begin{align*} r_{xy} &= \frac{1}{n}\sum_{i = 1}^{n}{z_{x_{i}}\cdot z_{y_{i}}} \\ &= \frac{1}{6}\sum_{i = 1}^{6}{z_{x_{i}}\cdot z_{y_{i}}} \\ &= \frac{1}{6}\left\lbrack z_{x_{1}}\cdot z_{y_{1}} + z_{x_{2}}\cdot z_{y_{2}} + \ldots + z_{x_{6}}\cdot z_{y_{6}} \right\rbrack \\ &= \frac{1}{6}\left\lbrack (0.5)\cdot (0.71) + (1.09)\cdot (1.25) + \ldots + ((-1.29)) \cdot ((-1.36)) \right\rbrack = 0.98 \end{align*} \]
BONUS: Überprüfen Sie Ihre Ergebnisse aus allen Teilaufgaben in R.
TippLösungx <- c(4.6, 5.1, 4.3, 3, 5, 3.1)y <- c(6.6, 7.1, 5.9, 4.8, 6.6, 4.7)mean(x)[1] 4.183333mean(y)[1] 5.95# Kovarianz von x und y # VORSICHT! Der Befehl cov() berechnet nicht die empirische Kovarianz! # Deshalb muss die Formel hier selbst nachgebaut werden: cov_xy <- sum((x - mean(x)) * (y - mean(y))) / 6 cov_xy[1] 0.7608333# VORSICHT! Der Befehl sd() berechnet nicht die empirische Standardabweichung! # Deshalb muss die Formel hier selbst nachgebaut werden: var_x <- sum((x - mean(x))^2) / 6 sd_x <- sqrt(var_x) sd_x[1] 0.8434387var_y <- sum((y - mean(y))^2) / 6 sd_y <- sqrt(var_y) sd_y[1] 0.917878# z-Standardisierung für x (x - mean(x)) / sd_x[1] 0.4940094 1.0868207 0.1383226 -1.4029867 0.9682584 -1.2844245# z-Standardisierung für y (y - mean(y)) / sd_y[1] 0.70815512 1.25288983 -0.05447347 -1.25288983 0.70815512 -1.36183678# Korrelation von x und y cor(x,y)[1] 0.9827681
| Medienkonsum in Stunden/Tag | Schlaf in Stunden | |
|---|---|---|
| Schüler 1 | 5.4 | 7.4 |
| Schüler 2 | 5.7 | 7.5 |
| Schüler 3 | 5.6 | 7.4 |
| Schüler 4 | 6.7 | 8.2 |
| Schüler 5 | 5.3 | 7.4 |
| Schüler 6 | 5.1 | 7.1 |
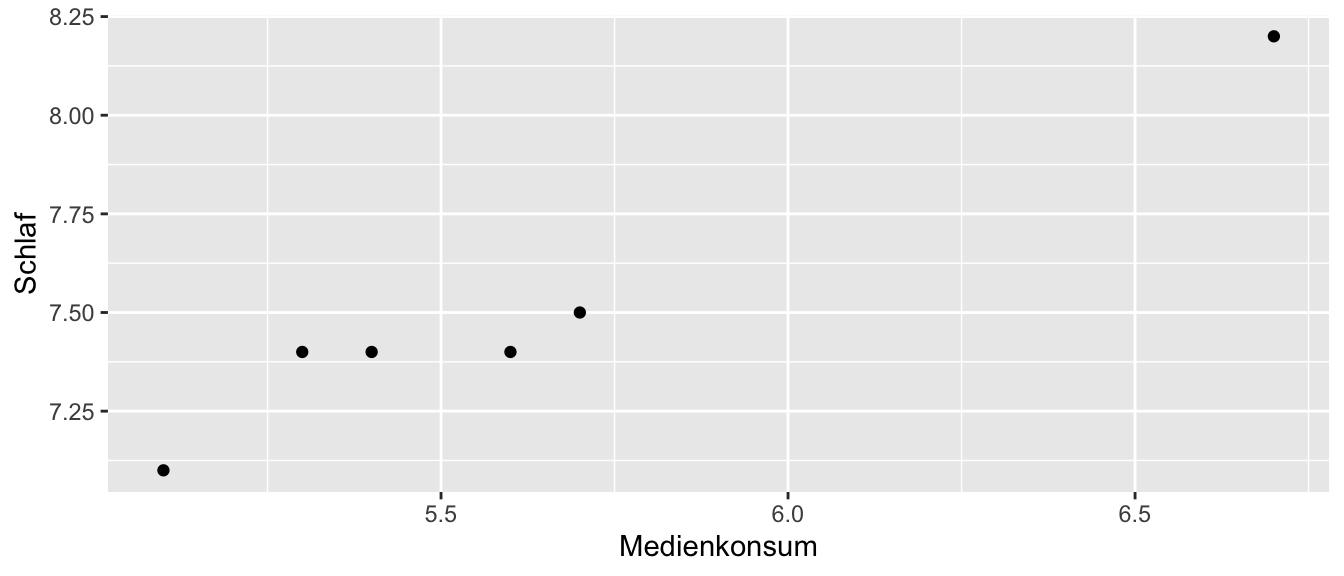
Welche Richtung hat der Zusammenhang? Drücken Sie diesen in Worten aus.
TippLösungEs liegt ein gleichgerichteter Zusammenhang vor. Je höher der tägliche Medienkonsum der Schüler ist, desto höher schlafen sie im Durchschnitt (bzw. umgekehrt).
Berechnen Sie die Kovarianz und interpretieren Sie diese.
TippLösung\[\bar{x} = 5.63\]
\[\bar{y} = 7.5\]
\[ \begin{align*} {cov}_{emp}(x,\ y) &= \frac{1}{n}\sum_{i = 1}^{n}\left( x_{i} - \bar{x} \right)\left( y_{i} - \bar{y} \right) \\ &= \frac{1}{6}\sum_{i = 1}^{6}\left( x_{i} - 5.63 \right)\left( y_{i} - 7.5 \right) \\ &= \frac{1}{6}\left\lbrack \left( x_{1} - 5.63 \right)\left( y_{1} - 7.5 \right) + \left( x_{2} - 5.63 \right)\left( y_{2} - 7.5 \right) + \ldots + \left( x_{5} - 5.63 \right)\left( y_{5} - 7.5 \right) \right\rbrack \\ &= \frac{1}{6}\left\lbrack (5.4 - 5.63)(7.4 - 7.5) + (5.7 - 5.63)(7.5 - 7.5) + \ldots + (5.1 - 5.63)(7.1 - 7.5) \right\rbrack = 0.17 \end{align*} \] Da an der Kovarianz lediglich die Richtung des Zusammenhangs abgelesen werden kann, können wir nur sagen, dass ein gleichgerichteter Zusammenhang der Variablen Medienkonsum und Schlaf vorliegt.
Berechnen Sie für die beiden Variablen jeweils die Standardabweichung \(s_{emp}\).
TippLösung\[ \begin{align*} s_{emp_x} &= \sqrt{\frac{1}{n} \sum_{i = 1}^n (x_i - \bar{x})^2} \\ &= \sqrt{\frac{1}{6} [(5.4 - 5.63)^2 + (5.7 - 5.63)^2 + (5.6 - 5.63)^2 + (6.7 - 5.63)^2 + (5.3 - 5.63)^2 + (5.1 - 5.63)^2]} \\ &= \sqrt{\frac{1}{6} 1.56} \\ &= \sqrt{0.26} \\ &= 0.51 \\ s_{emp_y} &= \sqrt{\frac{1}{n} \sum_{i = 1}^n (y_i - \bar{y})^2} \\ &= \ ... \\ &= 0.33 \end{align*} \]
Z-standardisieren Sie beide Variablen.
TippLösung\[ z_{x_i} = \frac{x_i - \bar{x}}{\sqrt{s^2_{emp_x}}} \text{ bzw. } z_{x_i} = \frac{y_i - \bar{y}}{\sqrt{s^2_{emp_y}}} \]
Also z.B. für \(x_1 = 5.4\), \(\bar{x} = 5.63\) und \(s_{emp_x} = 0.51\):
\[ z_{x_1} = \frac{x_1 - \bar{x}}{\sqrt{s^2_{emp_x}}} = \frac{5.4 - 5.63}{0.51} \approx -0.46 \]
Medienkonsum in Stunden/Tag \(z_{Medienkonsum}\) Schlaf in Stunden \(z_{Schlaf}\) Schüler 1 5.4 -0.46 7.4 -0.30 Schüler 2 5.7 0.13 7.5 0.00 Schüler 3 5.6 -0.07 7.4 -0.30 Schüler 4 6.7 2.09 8.2 2.12 Schüler 5 5.3 -0.65 7.4 -0.30 Schüler 6 5.1 -1.05 7.1 -1.21 Überprüfen Sie Ihr Ergebnis auch, indem Sie den Mittelwert der \(z\)-Werte \(z_{x_i}\) bzw. \(z_{y_i}\) berechnen. Welcher Wert sollte (nach Rundung ungefähr) dabei herauskommen?
TippLösung\[\begin{align*} \bar{z}_x &= \frac{1}{6} \sum_{i = 1}^n z_{x_i} = \frac{1}{6} \cdot \lbrack (-0.46) + (0.13) + (-0.07) + (2.09) + (-0.65) + (-1.05) \rbrack \approx 0 \\ \bar{z}_y &= \frac{1}{6} \sum_{i = 1}^n z_{y_i} = \frac{1}{6} \cdot \lbrack (-0.3) + (0) + (-0.3) + (2.12) + (-0.3) + (-1.21) \rbrack \approx 0 \end{align*}\]
Berechnen Sie die Korrelation.
TippLösung\[ \begin{align*} r_{xy} &= \frac{1}{n}\sum_{i = 1}^{n}{z_{x_{i}}\cdot z_{y_{i}}} \\ &= \frac{1}{6}\sum_{i = 1}^{6}{z_{x_{i}}\cdot z_{y_{i}}} \\ &= \frac{1}{6}\left\lbrack z_{x_{1}}\cdot z_{y_{1}} + z_{x_{2}}\cdot z_{y_{2}} + \ldots + z_{x_{6}}\cdot z_{y_{6}} \right\rbrack \\ &= \frac{1}{6}\left\lbrack (-0.46)\cdot (-0.3) + (0.13)\cdot (0) + \ldots + ((-1.05)) \cdot ((-1.21)) \right\rbrack = 1.01 \end{align*} \]
BONUS: Überprüfen Sie Ihre Ergebnisse aus allen Teilaufgaben in R.
TippLösungx <- c(5.4, 5.7, 5.6, 6.7, 5.3, 5.1)y <- c(7.4, 7.5, 7.4, 8.2, 7.4, 7.1)mean(x)[1] 5.633333mean(y)[1] 7.5# Kovarianz von x und y # VORSICHT! Der Befehl cov() berechnet nicht die empirische Kovarianz! # Deshalb muss die Formel hier selbst nachgebaut werden: cov_xy <- sum((x - mean(x)) * (y - mean(y))) / 6 cov_xy[1] 0.17# VORSICHT! Der Befehl sd() berechnet nicht die empirische Standardabweichung! # Deshalb muss die Formel hier selbst nachgebaut werden: var_x <- sum((x - mean(x))^2) / 6 sd_x <- sqrt(var_x) sd_x[1] 0.5153208var_y <- sum((y - mean(y))^2) / 6 sd_y <- sqrt(var_y) sd_y[1] 0.3366502# z-Standardisierung für x (x - mean(x)) / sd_x[1] -0.45279236 0.12936925 -0.06468462 2.06990793 -0.64684623 -1.03495396# z-Standardisierung für y (y - mean(y)) / sd_y[1] -0.2970443 0.0000000 -0.2970443 2.0793098 -0.2970443 -1.1881771# Korrelation von x und y cor(x,y)[1] 0.979924
| Medienkonsum in Stunden/Tag | Schlaf in Stunden | |
|---|---|---|
| Schüler 1 | 4.0 | 7.7 |
| Schüler 2 | 3.3 | 8.8 |
| Schüler 3 | 5.3 | 6.1 |
| Schüler 4 | 3.8 | 7.8 |
| Schüler 5 | 5.2 | 7.0 |
| Schüler 6 | 4.9 | 6.8 |
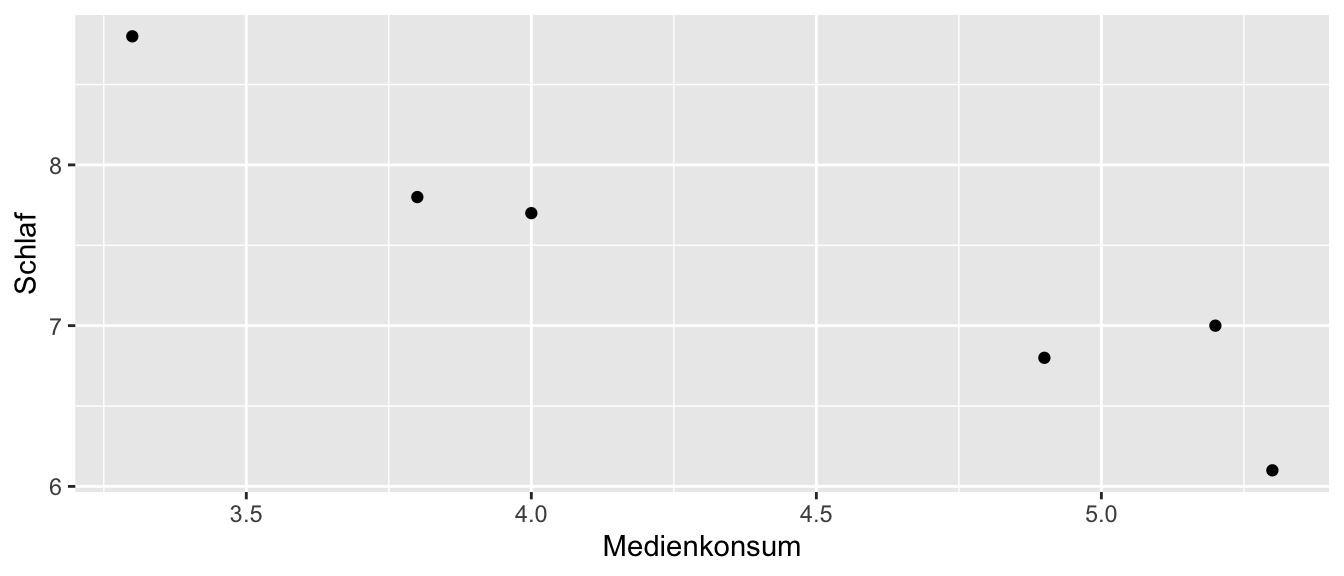
Welche Richtung hat der Zusammenhang? Drücken Sie diesen in Worten aus.
TippLösungEs liegt ein entgegengerichteter Zusammenhang vor. Je höher der tägliche Medienkonsum der Schüler ist, desto niedriger schlafen sie im Durchschnitt (bzw. umgekehrt).
Berechnen Sie die Kovarianz und interpretieren Sie diese.
TippLösung\[\bar{x} = 4.42\]
\[\bar{y} = 7.37\]
\[ \begin{align*} {cov}_{emp}(x,\ y) &= \frac{1}{n}\sum_{i = 1}^{n}\left( x_{i} - \bar{x} \right)\left( y_{i} - \bar{y} \right) \\ &= \frac{1}{6}\sum_{i = 1}^{6}\left( x_{i} - 4.42 \right)\left( y_{i} - 7.37 \right) \\ &= \frac{1}{6}\left\lbrack \left( x_{1} - 4.42 \right)\left( y_{1} - 7.37 \right) + \left( x_{2} - 4.42 \right)\left( y_{2} - 7.37 \right) + \ldots + \left( x_{5} - 4.42 \right)\left( y_{5} - 7.37 \right) \right\rbrack \\ &= \frac{1}{6}\left\lbrack (4 - 4.42)(7.7 - 7.37) + (3.3 - 4.42)(8.8 - 7.37) + \ldots + (4.9 - 4.42)(6.8 - 7.37) \right\rbrack = -0.61 \end{align*} \] Da an der Kovarianz lediglich die Richtung des Zusammenhangs abgelesen werden kann, können wir nur sagen, dass ein gegengerichteter Zusammenhang der Variablen Medienkonsum und Schlaf vorliegt.
Berechnen Sie für die beiden Variablen jeweils die Standardabweichung \(s_{emp}\).
TippLösung\[ \begin{align*} s_{emp_x} &= \sqrt{\frac{1}{n} \sum_{i = 1}^n (x_i - \bar{x})^2} \\ &= \sqrt{\frac{1}{6} [(4 - 4.42)^2 + (3.3 - 4.42)^2 + (5.3 - 4.42)^2 + (3.8 - 4.42)^2 + (5.2 - 4.42)^2 + (4.9 - 4.42)^2]} \\ &= \sqrt{\frac{1}{6} 3.42} \\ &= \sqrt{0.57} \\ &= 0.75 \\ s_{emp_y} &= \sqrt{\frac{1}{n} \sum_{i = 1}^n (y_i - \bar{y})^2} \\ &= \ ... \\ &= 0.85 \end{align*} \]
Z-standardisieren Sie beide Variablen.
TippLösung\[ z_{x_i} = \frac{x_i - \bar{x}}{\sqrt{s^2_{emp_x}}} \text{ bzw. } z_{x_i} = \frac{y_i - \bar{y}}{\sqrt{s^2_{emp_y}}} \]
Also z.B. für \(x_1 = 4\), \(\bar{x} = 4.42\) und \(s_{emp_x} = 0.75\):
\[ z_{x_1} = \frac{x_1 - \bar{x}}{\sqrt{s^2_{emp_x}}} = \frac{4 - 4.42}{0.75} \approx -0.56 \]
Medienkonsum in Stunden/Tag \(z_{Medienkonsum}\) Schlaf in Stunden \(z_{Schlaf}\) Schüler 1 4.0 -0.56 7.7 0.39 Schüler 2 3.3 -1.49 8.8 1.69 Schüler 3 5.3 1.18 6.1 -1.49 Schüler 4 3.8 -0.82 7.8 0.51 Schüler 5 5.2 1.04 7.0 -0.43 Schüler 6 4.9 0.64 6.8 -0.67 Überprüfen Sie Ihr Ergebnis auch, indem Sie den Mittelwert der \(z\)-Werte \(z_{x_i}\) bzw. \(z_{y_i}\) berechnen. Welcher Wert sollte (nach Rundung ungefähr) dabei herauskommen?
TippLösung\[\begin{align*} \bar{z}_x &= \frac{1}{6} \sum_{i = 1}^n z_{x_i} = \frac{1}{6} \cdot \lbrack (-0.56) + (-1.49) + (1.18) + (-0.82) + (1.04) + (0.64) \rbrack \approx 0 \\ \bar{z}_y &= \frac{1}{6} \sum_{i = 1}^n z_{y_i} = \frac{1}{6} \cdot \lbrack (0.39) + (1.69) + (-1.49) + (0.51) + (-0.43) + (-0.67) \rbrack \approx 0 \end{align*}\]
Berechnen Sie die Korrelation.
TippLösung\[ \begin{align*} r_{xy} &= \frac{1}{n}\sum_{i = 1}^{n}{z_{x_{i}}\cdot z_{y_{i}}} \\ &= \frac{1}{6}\sum_{i = 1}^{6}{z_{x_{i}}\cdot z_{y_{i}}} \\ &= \frac{1}{6}\left\lbrack z_{x_{1}}\cdot z_{y_{1}} + z_{x_{2}}\cdot z_{y_{2}} + \ldots + z_{x_{6}}\cdot z_{y_{6}} \right\rbrack \\ &= \frac{1}{6}\left\lbrack (-0.56)\cdot (0.39) + (-1.49)\cdot (1.69) + \ldots + ((0.64)) \cdot ((-0.67)) \right\rbrack = -0.97 \end{align*} \]
BONUS: Überprüfen Sie Ihre Ergebnisse aus allen Teilaufgaben in R.
TippLösungx <- c(4, 3.3, 5.3, 3.8, 5.2, 4.9)y <- c(7.7, 8.8, 6.1, 7.8, 7, 6.8)mean(x)[1] 4.416667mean(y)[1] 7.366667# Kovarianz von x und y # VORSICHT! Der Befehl cov() berechnet nicht die empirische Kovarianz! # Deshalb muss die Formel hier selbst nachgebaut werden: cov_xy <- sum((x - mean(x)) * (y - mean(y))) / 6 cov_xy[1] -0.6144444# VORSICHT! Der Befehl sd() berechnet nicht die empirische Standardabweichung! # Deshalb muss die Formel hier selbst nachgebaut werden: var_x <- sum((x - mean(x))^2) / 6 sd_x <- sqrt(var_x) sd_x[1] 0.7559027var_y <- sum((y - mean(y))^2) / 6 sd_y <- sqrt(var_y) sd_y[1] 0.8576454# z-Standardisierung für x (x - mean(x)) / sd_x[1] -0.5512173 -1.4772624 1.1685807 -0.8158016 1.0362886 0.6394121# z-Standardisierung für y (y - mean(y)) / sd_y[1] 0.3886610 1.6712425 -1.4769119 0.5052593 -0.4275271 -0.6607238# Korrelation von x und y cor(x,y)[1] -0.9477832
| Medienkonsum in Stunden/Tag | Schlaf in Stunden | |
|---|---|---|
| Schüler 1 | 5.0 | 7.8 |
| Schüler 2 | 5.2 | 6.7 |
| Schüler 3 | 3.0 | 9.1 |
| Schüler 4 | 6.0 | 6.2 |
| Schüler 5 | 5.9 | 5.6 |
| Schüler 6 | 5.2 | 6.0 |
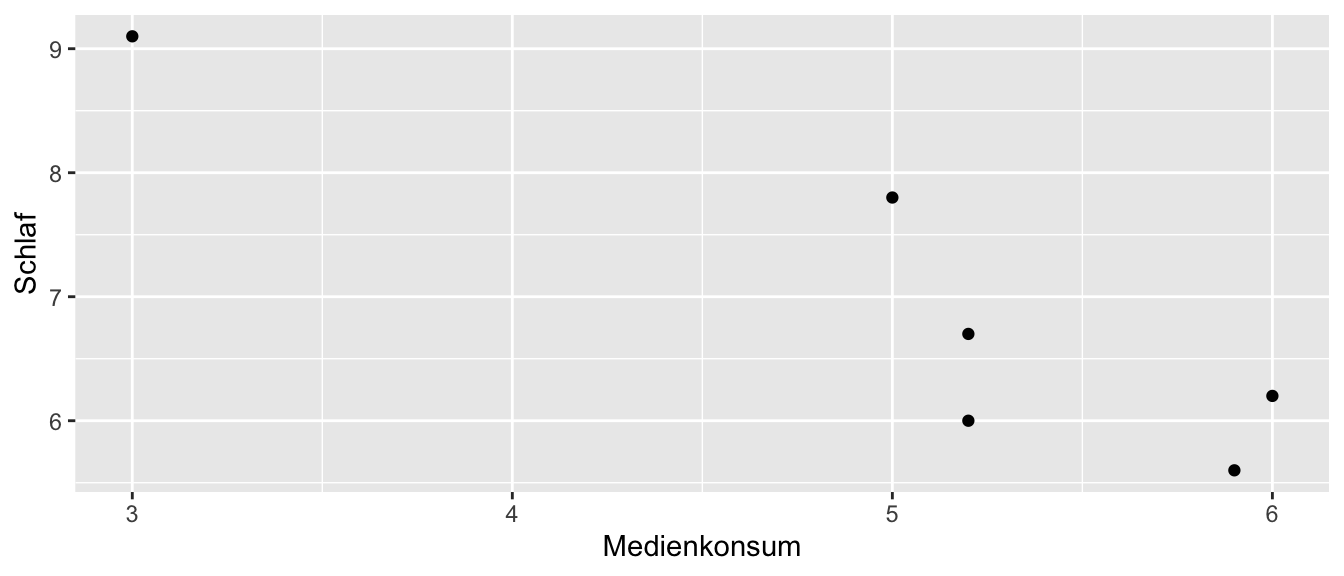
Welche Richtung hat der Zusammenhang? Drücken Sie diesen in Worten aus.
TippLösungEs liegt ein entgegengerichteter Zusammenhang vor. Je höher der tägliche Medienkonsum der Schüler ist, desto niedriger schlafen sie im Durchschnitt (bzw. umgekehrt).
Berechnen Sie die Kovarianz und interpretieren Sie diese.
TippLösung\[\bar{x} = 5.05\]
\[\bar{y} = 6.9\]
\[ \begin{align*} {cov}_{emp}(x,\ y) &= \frac{1}{n}\sum_{i = 1}^{n}\left( x_{i} - \bar{x} \right)\left( y_{i} - \bar{y} \right) \\ &= \frac{1}{6}\sum_{i = 1}^{6}\left( x_{i} - 5.05 \right)\left( y_{i} - 6.9 \right) \\ &= \frac{1}{6}\left\lbrack \left( x_{1} - 5.05 \right)\left( y_{1} - 6.9 \right) + \left( x_{2} - 5.05 \right)\left( y_{2} - 6.9 \right) + \ldots + \left( x_{5} - 5.05 \right)\left( y_{5} - 6.9 \right) \right\rbrack \\ &= \frac{1}{6}\left\lbrack (5 - 5.05)(7.8 - 6.9) + (5.2 - 5.05)(6.7 - 6.9) + \ldots + (5.2 - 5.05)(6 - 6.9) \right\rbrack = -1.08 \end{align*} \] Da an der Kovarianz lediglich die Richtung des Zusammenhangs abgelesen werden kann, können wir nur sagen, dass ein gegengerichteter Zusammenhang der Variablen Medienkonsum und Schlaf vorliegt.
Berechnen Sie für die beiden Variablen jeweils die Standardabweichung \(s_{emp}\).
TippLösung\[ \begin{align*} s_{emp_x} &= \sqrt{\frac{1}{n} \sum_{i = 1}^n (x_i - \bar{x})^2} \\ &= \sqrt{\frac{1}{6} [(5 - 5.05)^2 + (5.2 - 5.05)^2 + (3 - 5.05)^2 + (6 - 5.05)^2 + (5.9 - 5.05)^2 + (5.2 - 5.05)^2]} \\ &= \sqrt{\frac{1}{6} 5.88} \\ &= \sqrt{0.98} \\ &= 0.99 \\ s_{emp_y} &= \sqrt{\frac{1}{n} \sum_{i = 1}^n (y_i - \bar{y})^2} \\ &= \ ... \\ &= 1.2 \end{align*} \]
Z-standardisieren Sie beide Variablen.
TippLösung\[ z_{x_i} = \frac{x_i - \bar{x}}{\sqrt{s^2_{emp_x}}} \text{ bzw. } z_{x_i} = \frac{y_i - \bar{y}}{\sqrt{s^2_{emp_y}}} \]
Also z.B. für \(x_1 = 5\), \(\bar{x} = 5.05\) und \(s_{emp_x} = 0.99\):
\[ z_{x_1} = \frac{x_1 - \bar{x}}{\sqrt{s^2_{emp_x}}} = \frac{5 - 5.05}{0.99} \approx -0.05 \]
Medienkonsum in Stunden/Tag \(z_{Medienkonsum}\) Schlaf in Stunden \(z_{Schlaf}\) Schüler 1 5.0 -0.05 7.8 0.75 Schüler 2 5.2 0.15 6.7 -0.17 Schüler 3 3.0 -2.07 9.1 1.83 Schüler 4 6.0 0.96 6.2 -0.58 Schüler 5 5.9 0.86 5.6 -1.08 Schüler 6 5.2 0.15 6.0 -0.75 Überprüfen Sie Ihr Ergebnis auch, indem Sie den Mittelwert der \(z\)-Werte \(z_{x_i}\) bzw. \(z_{y_i}\) berechnen. Welcher Wert sollte (nach Rundung ungefähr) dabei herauskommen?
TippLösung\[\begin{align*} \bar{z}_x &= \frac{1}{6} \sum_{i = 1}^n z_{x_i} = \frac{1}{6} \cdot \lbrack (-0.05) + (0.15) + (-2.07) + (0.96) + (0.86) + (0.15) \rbrack \approx 0 \\ \bar{z}_y &= \frac{1}{6} \sum_{i = 1}^n z_{y_i} = \frac{1}{6} \cdot \lbrack (0.75) + (-0.17) + (1.83) + (-0.58) + (-1.08) + (-0.75) \rbrack \approx 0 \end{align*}\]
Berechnen Sie die Korrelation.
TippLösung\[ \begin{align*} r_{xy} &= \frac{1}{n}\sum_{i = 1}^{n}{z_{x_{i}}\cdot z_{y_{i}}} \\ &= \frac{1}{6}\sum_{i = 1}^{6}{z_{x_{i}}\cdot z_{y_{i}}} \\ &= \frac{1}{6}\left\lbrack z_{x_{1}}\cdot z_{y_{1}} + z_{x_{2}}\cdot z_{y_{2}} + \ldots + z_{x_{6}}\cdot z_{y_{6}} \right\rbrack \\ &= \frac{1}{6}\left\lbrack (-0.05)\cdot (0.75) + (0.15)\cdot (-0.17) + \ldots + ((0.15)) \cdot ((-0.75)) \right\rbrack = -0.91 \end{align*} \]
BONUS: Überprüfen Sie Ihre Ergebnisse aus allen Teilaufgaben in R.
TippLösungx <- c(5, 5.2, 3, 6, 5.9, 5.2)y <- c(7.8, 6.7, 9.1, 6.2, 5.6, 6)mean(x)[1] 5.05mean(y)[1] 6.9# Kovarianz von x und y # VORSICHT! Der Befehl cov() berechnet nicht die empirische Kovarianz! # Deshalb muss die Formel hier selbst nachgebaut werden: cov_xy <- sum((x - mean(x)) * (y - mean(y))) / 6 cov_xy[1] -1.081667# VORSICHT! Der Befehl sd() berechnet nicht die empirische Standardabweichung! # Deshalb muss die Formel hier selbst nachgebaut werden: var_x <- sum((x - mean(x))^2) / 6 sd_x <- sqrt(var_x) sd_x[1] 0.9895285var_y <- sum((y - mean(y))^2) / 6 sd_y <- sqrt(var_y) sd_y[1] 1.202775# z-Standardisierung für x (x - mean(x)) / sd_x[1] -0.05052912 0.15158735 -2.07169373 0.96005319 0.85899496 0.15158735# z-Standardisierung für y (y - mean(y)) / sd_y[1] 0.7482699 -0.1662822 1.8291042 -0.5819877 -1.0808343 -0.7482699# Korrelation von x und y cor(x,y)[1] -0.9088263