Übungsblatt 04

Wahrscheinlichkeitsverteilungen, Zufallsvariablen und Wahrscheinlichkeitsfunktionen

Hinweis

Die hier veröffentlichten Übungsaufgaben sind brandneu und deshalb noch nicht auf Herz und Nieren überprüft. Sollten Sie Fehler entdecken, geben Sie uns bitte unbedingt eine Rückmeldung an philipp.sckopke(at)psy.lmu.de, damit wir so bald wie möglich eine verbesserte Version online stellen können.

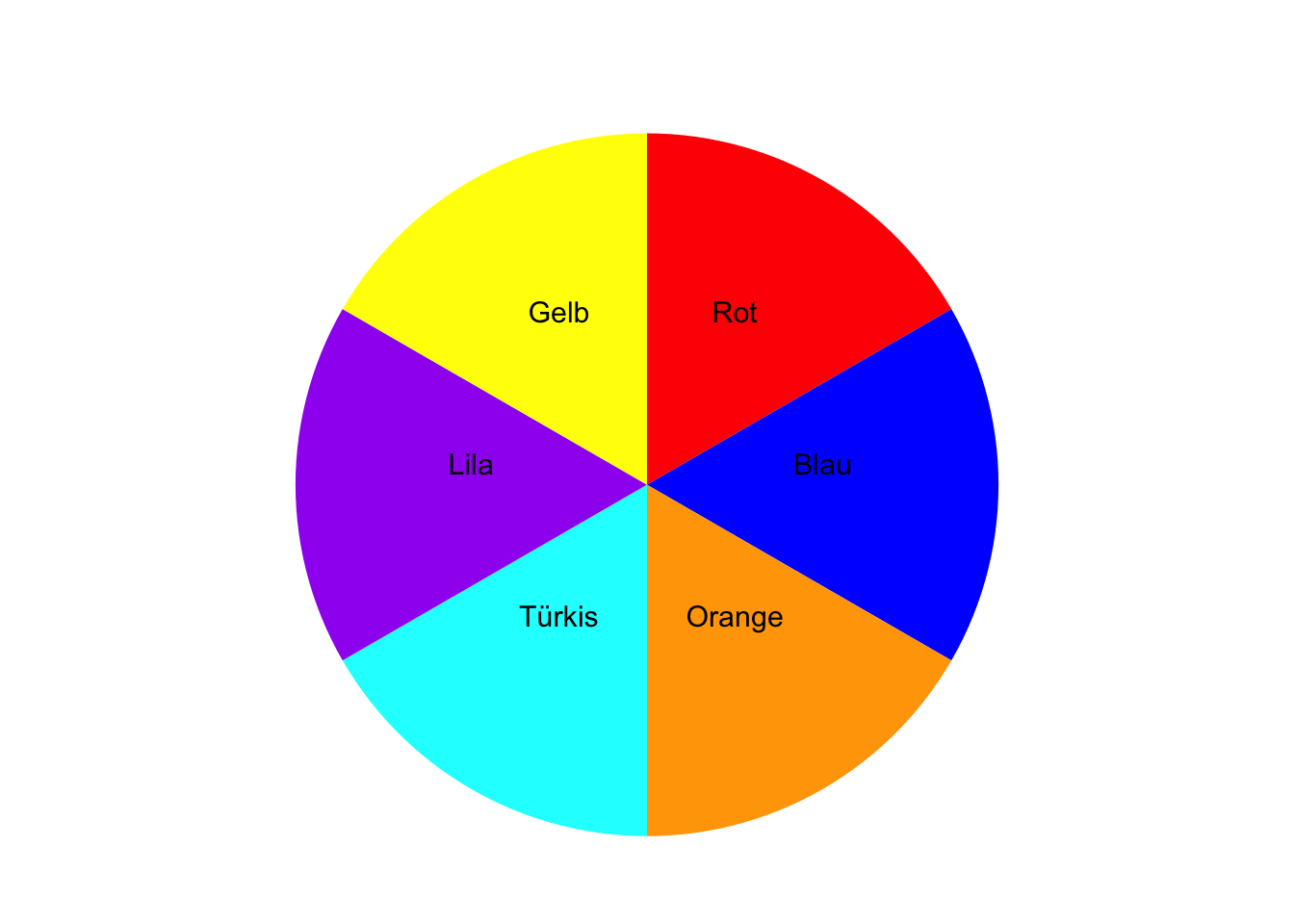
  1. Auf einer Kinomesse können Sie kostenlos an einem Gewinnspiel teilnehmen und einmal an einem Glücksrad drehen. Das Glücksrad bleibt auf einem Feld mit einer bestimmten Farbe stehen. Das Glücksrad besitzt Felder mit den Farben Rot, Blau, Orange, Türkis, Lila und Gelb.

    1. Geben Sie die Ergebnismenge \(\Omega\) an.

      \(\Omega\) = {Rot, Blau, Orange, Türkis, Lila, Gelb}

    2. Geben Sie die Elementarereignisse an.

      Elementarereignisse sind: {Rot}, {Blau}, {Orange}, {Türkis}, {Lila}, {Gelb}

    3. Geben Sie die Wahrscheinlichkeit für die folgenden Ereignisse an. (Hinweis: Nehmen Sie an, dass alle Felder des Glücksrads gleich groß sind):

      1. \(A_1\): “Das Glücksrad bleibt auf dem Feld mit der Farbe Orange stehen.”

        \(P(A_1) = P(\{Orange\}) = \frac{1}{6}\)

      2. \(A_2\): “Das Glücksrad bleibt auf einem Feld mit der Farbe Gelb oder Türkis stehen.”

        \(P(A_2) = P(\{Gelb, Türkis\}) = P(\{Gelb\}) + P(\{Türkis\}) = \frac{1}{6} + \frac{1}{6} = \frac{2}{6}\)

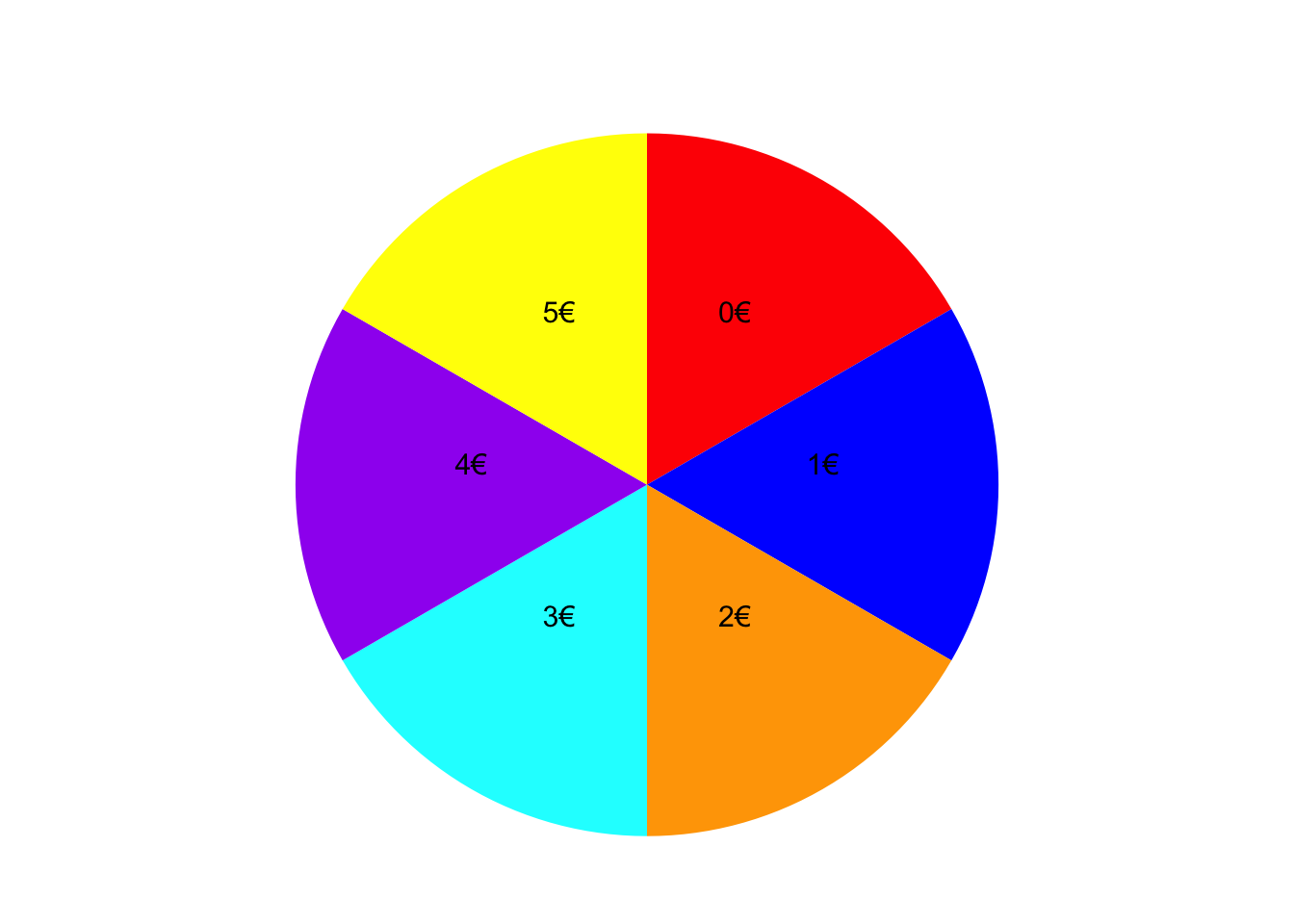
  2. Je nachdem auf welchem Feld das Glücksrad stehen bleibt, erhalten Sie einen Kino-Gutschein im Wert eines bestimmten Geldbetrags. Die Zufallsvariable \(X\) gibt den Wert des Gutscheins in Euro an, den Sie bei dem Gewinnspiel erhalten.

    1. Geben Sie den Träger der Zufallsvariable \(X\) an.

      \(T_{X}\) = {0, 1, 2, 3, 4, 5}

    2. Geben Sie die Elementarereignisse der Zufallsvariable \(X\) an.

      Elementarereignisse sind: {0}, {1}, {2}, {3}, {4}, {5}

    3. Geben Sie die Wahrscheinlichkeit für die folgenden Ereignisse an. (Hinweis: Nehmen Sie an, dass alle Felder des Glücksrads gleich groß sind):

      1. \(A_{X1}\): “Sie erhalten einen Gutschein im Wert von mindestens 1 Euro.

        \(P_X(A_{X1}) = P_X(\{1,2,3,4,5\}) = P(\{Blau,Orange,Türkis,Lila,Gelb\}) = \frac{5}{6} = 0.8333333\)

      2. \(A_{X2}\): “Sie erhalten einen Gutschein im Wert von weniger als 3 Euro.

        \(P_X(A_{X2}) = P_X(\{0,1,2\}) = P(\{Rot,Blau,Orange\}) = \frac{3}{6} = 0.5\)

  3. Angenommen, eine Kinokarte kostet 1 Euro.

    1. Geben Sie in Form einer Tabelle eine Zufallsvariable \(Y\) an, die angibt, ob ihr Gutschein nach dem Gewinnspiel für keine (0), eine (1), oder zwei (2) Kinokarten ausreicht.

      \(\omega\) Rot Blau Orange Türkis Lila Gelb
      x 0 1 2 3 4 5
      y 0 1 2 2 2 2

    2. Geben Sie den Träger \(T_{Y}\) dieser Zufallsvariable an.

      \(T_{Y}\) = {0, 1, 2}

    3. Geben Sie die Wahrscheinlichkeitsfunktion \(f\) von \(Y\) in Form einer Tabelle an.

      \(y\) 0 1 2
      \(f(y)\) \(\frac{1}{6}\) \(\frac{1}{6}\) \(\frac{4}{6}\)

    4. Geben Sie die Verteilungsfunktion \(F\) von \(Y\) in Form einer Tabelle an.

      \(y\) 0 1 2
      \(F(y)\) \(\frac{1}{6}\) \(\frac{2}{6}\) \(\frac{6}{6}\)

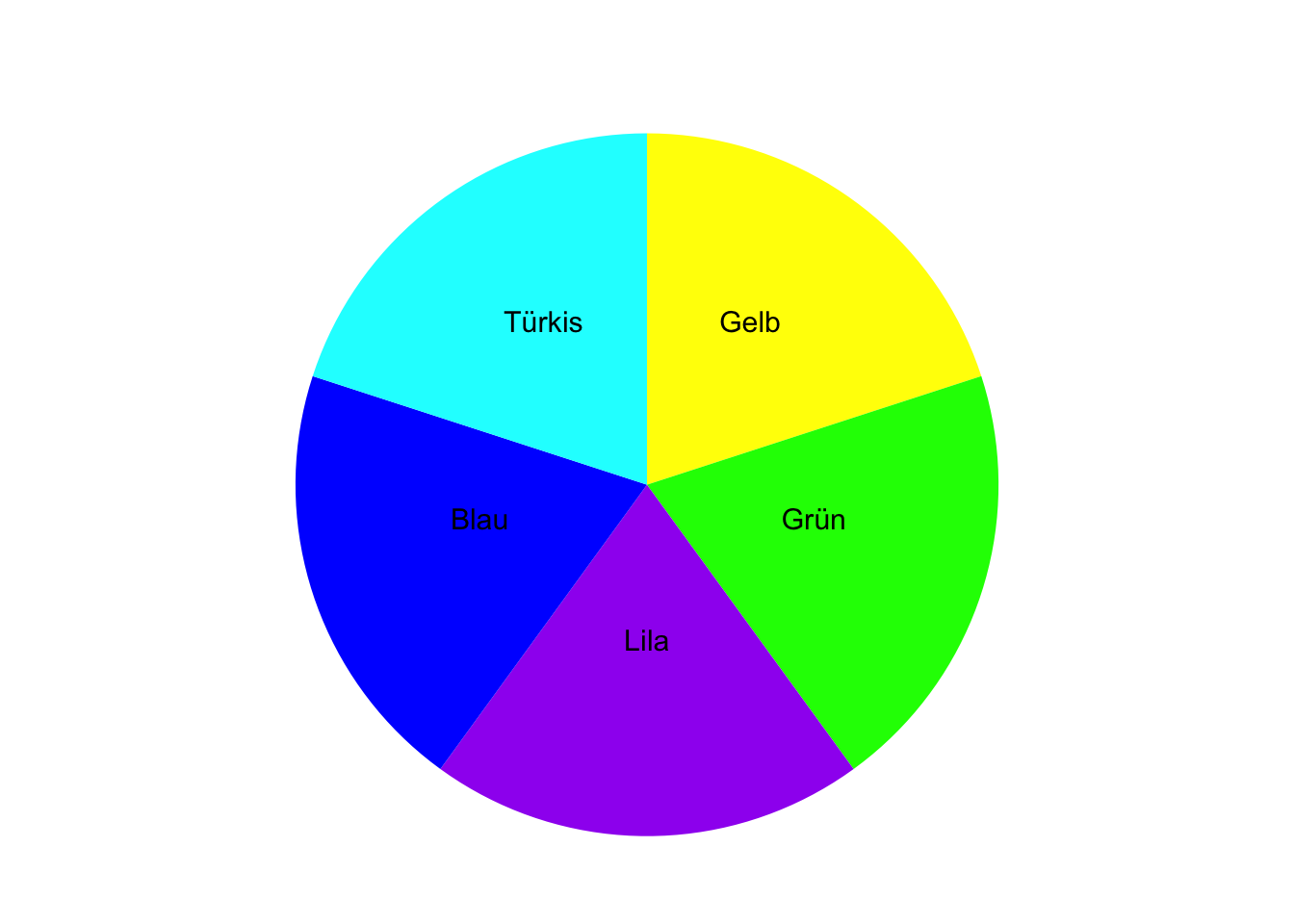
  1. Auf einer Kinomesse können Sie kostenlos an einem Gewinnspiel teilnehmen und einmal an einem Glücksrad drehen. Das Glücksrad bleibt auf einem Feld mit einer bestimmten Farbe stehen. Das Glücksrad besitzt Felder mit den Farben Gelb, Grün, Lila, Blau und Türkis.

    1. Geben Sie die Ergebnismenge \(\Omega\) an.

      \(\Omega\) = {Gelb, Grün, Lila, Blau, Türkis}

    2. Geben Sie die Elementarereignisse an.

      Elementarereignisse sind: {Gelb}, {Grün}, {Lila}, {Blau}, {Türkis}

    3. Geben Sie die Wahrscheinlichkeit für die folgenden Ereignisse an. (Hinweis: Nehmen Sie an, dass alle Felder des Glücksrads gleich groß sind):

      1. \(A_1\): “Das Glücksrad bleibt auf dem Feld mit der Farbe Gelb stehen.”

        \(P(A_1) = P(\{Gelb\}) = \frac{1}{5}\)

      2. \(A_2\): “Das Glücksrad bleibt auf einem Feld mit der Farbe Lila oder Blau stehen.”

        \(P(A_2) = P(\{Lila, Blau\}) = P(\{Lila\}) + P(\{Blau\}) = \frac{1}{5} + \frac{1}{5} = \frac{2}{5}\)

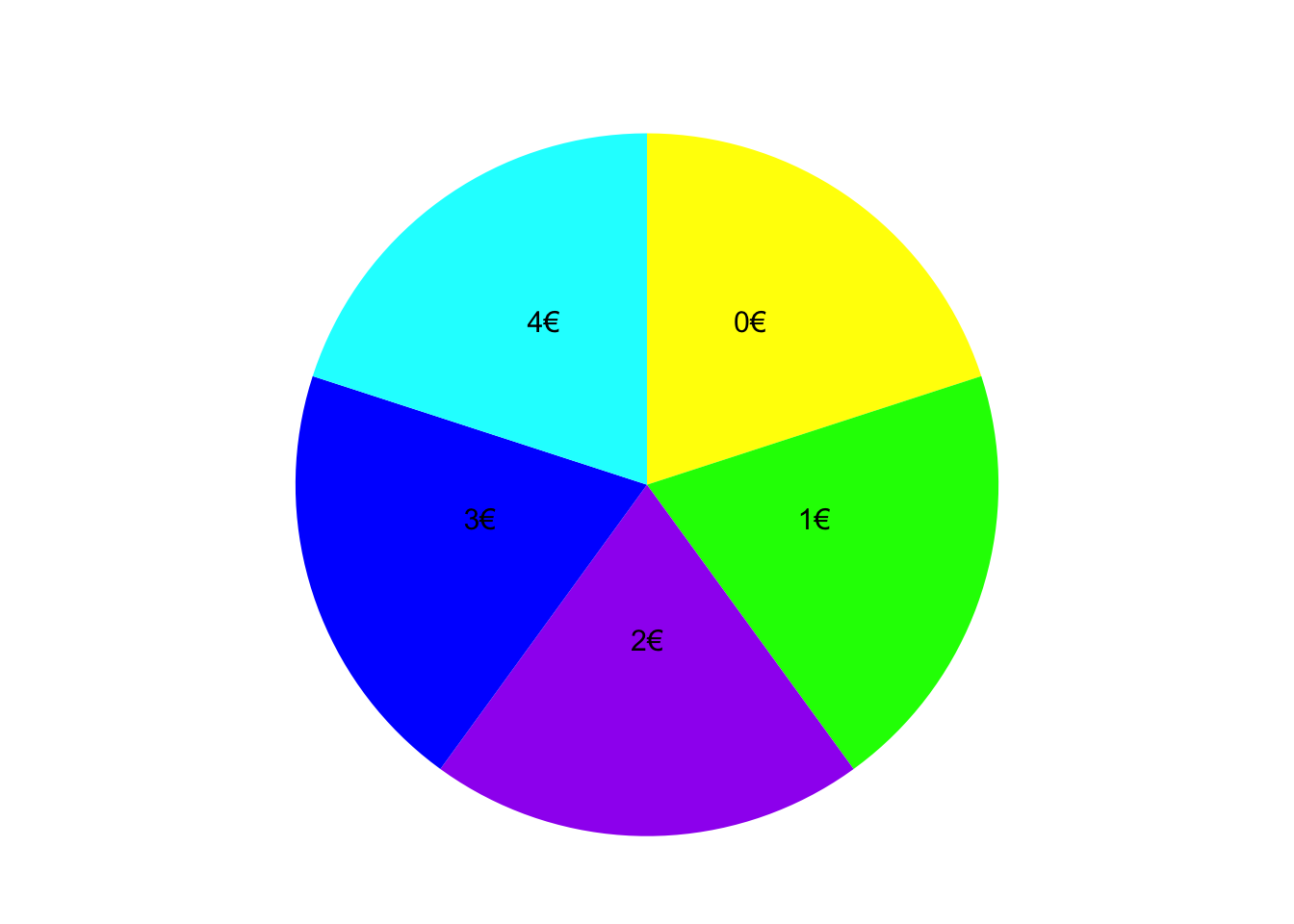
  2. Je nachdem auf welchem Feld das Glücksrad stehen bleibt, erhalten Sie einen Kino-Gutschein im Wert eines bestimmten Geldbetrags. Die Zufallsvariable \(X\) gibt den Wert des Gutscheins in Euro an, den Sie bei dem Gewinnspiel erhalten.

    1. Geben Sie den Träger der Zufallsvariable \(X\) an.

      \(T_{X}\) = {0, 1, 2, 3, 4}

    2. Geben Sie die Elementarereignisse der Zufallsvariable \(X\) an.

      Elementarereignisse sind: {0}, {1}, {2}, {3}, {4}

    3. Geben Sie die Wahrscheinlichkeit für die folgenden Ereignisse an. (Hinweis: Nehmen Sie an, dass alle Felder des Glücksrads gleich groß sind):

      1. \(A_{X1}\): “Sie erhalten einen Gutschein im Wert von mindestens 4 Euro.

        \(P_X(A_{X1}) = P_X(\{4\}) = P(\{Türkis\}) = \frac{1}{5} = 0.2\)

      2. \(A_{X2}\): “Sie erhalten einen Gutschein im Wert von weniger als 1 Euro.

        \(P_X(A_{X2}) = P_X(\{0\}) = P(\{Gelb\}) = \frac{1}{5} = 0.2\)

  3. Angenommen, eine Kinokarte kostet 1 Euro.

    1. Geben Sie in Form einer Tabelle eine Zufallsvariable \(Y\) an, die angibt, ob ihr Gutschein nach dem Gewinnspiel für keine (0), eine (1), oder zwei (2) Kinokarten ausreicht.

      \(\omega\) Gelb Grün Lila Blau Türkis
      x 0 1 2 3 4
      y 0 1 2 2 2

    2. Geben Sie den Träger \(T_{Y}\) dieser Zufallsvariable an.

      \(T_{Y}\) = {0, 1, 2}

    3. Geben Sie die Wahrscheinlichkeitsfunktion \(f\) von \(Y\) in Form einer Tabelle an.

      \(y\) 0 1 2
      \(f(y)\) \(\frac{1}{5}\) \(\frac{1}{5}\) \(\frac{3}{5}\)

    4. Geben Sie die Verteilungsfunktion \(F\) von \(Y\) in Form einer Tabelle an.

      \(y\) 0 1 2
      \(F(y)\) \(\frac{1}{5}\) \(\frac{2}{5}\) \(\frac{5}{5}\)

  1. Auf einer Kinomesse können Sie kostenlos an einem Gewinnspiel teilnehmen und einmal an einem Glücksrad drehen. Das Glücksrad bleibt auf einem Feld mit einer bestimmten Farbe stehen. Das Glücksrad besitzt Felder mit den Farben Lila, Grün, Türkis, Gelb, Blau und Rot.

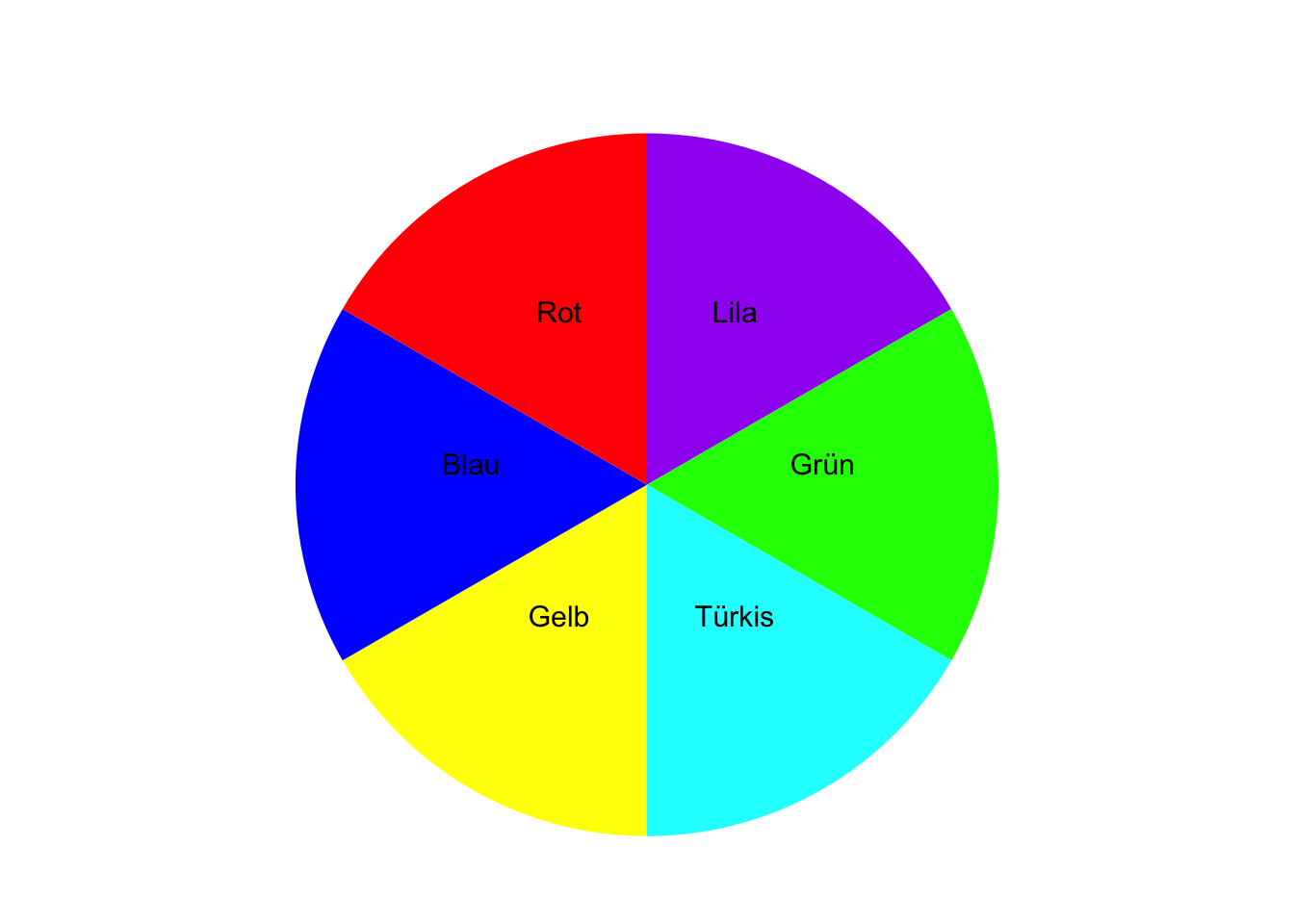
    1. Geben Sie die Ergebnismenge \(\Omega\) an.

      \(\Omega\) = {Lila, Grün, Türkis, Gelb, Blau, Rot}

    2. Geben Sie die Elementarereignisse an.

      Elementarereignisse sind: {Lila}, {Grün}, {Türkis}, {Gelb}, {Blau}, {Rot}

    3. Geben Sie die Wahrscheinlichkeit für die folgenden Ereignisse an. (Hinweis: Nehmen Sie an, dass alle Felder des Glücksrads gleich groß sind):

      1. \(A_1\): “Das Glücksrad bleibt auf dem Feld mit der Farbe Blau stehen.”

        \(P(A_1) = P(\{Blau\}) = \frac{1}{6}\)

      2. \(A_2\): “Das Glücksrad bleibt auf einem Feld mit der Farbe Blau oder Gelb stehen.”

        \(P(A_2) = P(\{Blau, Gelb\}) = P(\{Blau\}) + P(\{Gelb\}) = \frac{1}{6} + \frac{1}{6} = \frac{2}{6}\)

  2. Je nachdem auf welchem Feld das Glücksrad stehen bleibt, erhalten Sie einen Kino-Gutschein im Wert eines bestimmten Geldbetrags. Die Zufallsvariable \(X\) gibt den Wert des Gutscheins in Euro an, den Sie bei dem Gewinnspiel erhalten.

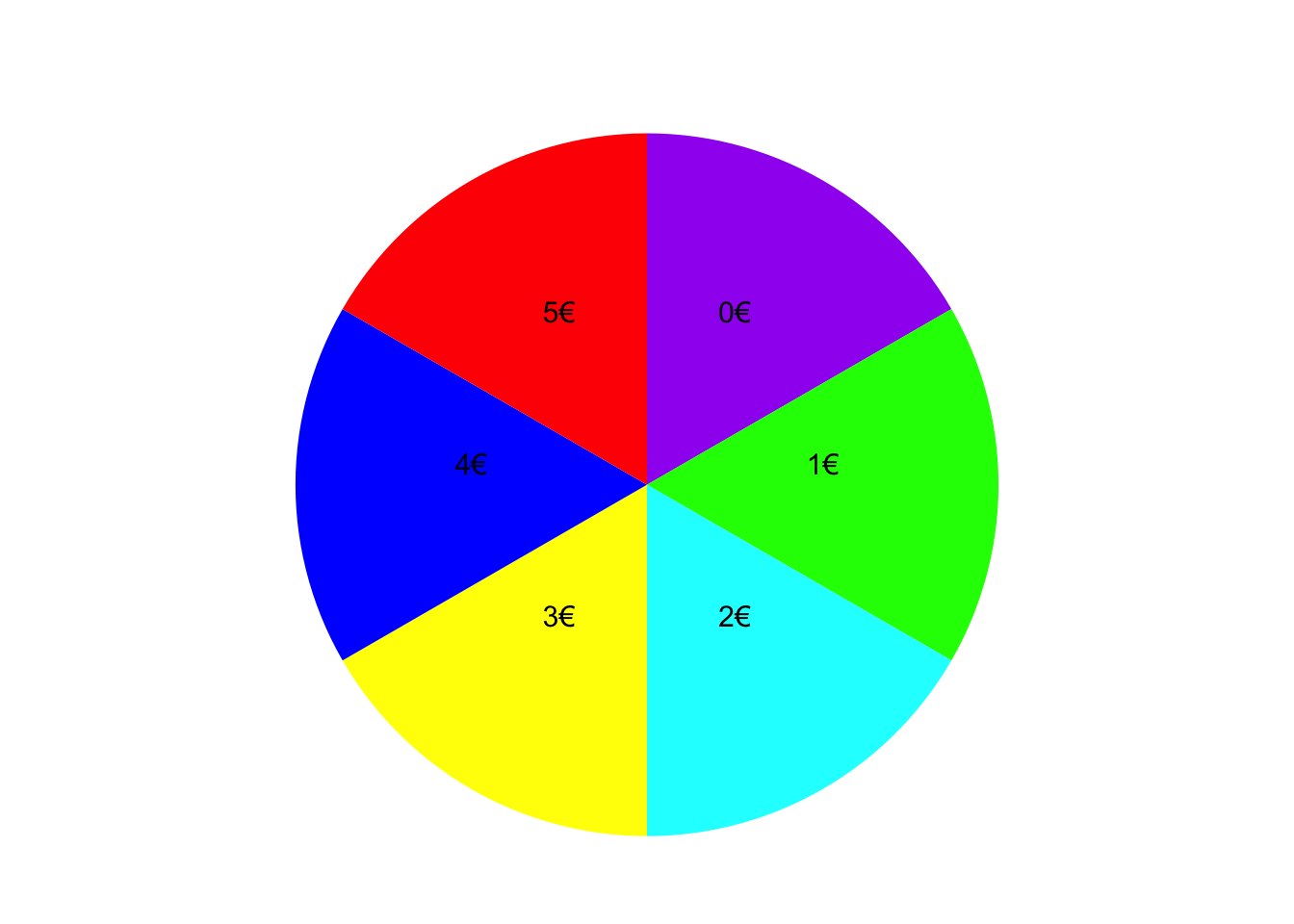
    1. Geben Sie den Träger der Zufallsvariable \(X\) an.

      \(T_{X}\) = {0, 1, 2, 3, 4, 5}

    2. Geben Sie die Elementarereignisse der Zufallsvariable \(X\) an.

      Elementarereignisse sind: {0}, {1}, {2}, {3}, {4}, {5}

    3. Geben Sie die Wahrscheinlichkeit für die folgenden Ereignisse an. (Hinweis: Nehmen Sie an, dass alle Felder des Glücksrads gleich groß sind):

      1. \(A_{X1}\): “Sie erhalten einen Gutschein im Wert von mindestens 3 Euro.

        \(P_X(A_{X1}) = P_X(\{3,4,5\}) = P(\{Gelb,Blau,Rot\}) = \frac{3}{6} = 0.5\)

      2. \(A_{X2}\): “Sie erhalten einen Gutschein im Wert von weniger als 4 Euro.

        \(P_X(A_{X2}) = P_X(\{0,1,2,3\}) = P(\{Lila,Grün,Türkis,Gelb\}) = \frac{4}{6} = 0.6666667\)

  3. Angenommen, eine Kinokarte kostet 2 Euro.

    1. Geben Sie in Form einer Tabelle eine Zufallsvariable \(Y\) an, die angibt, ob ihr Gutschein nach dem Gewinnspiel für keine (0), eine (1), oder zwei (2) Kinokarten ausreicht.

      \(\omega\) Lila Grün Türkis Gelb Blau Rot
      x 0 1 2 3 4 5
      y 0 0 1 1 2 2

    2. Geben Sie den Träger \(T_{Y}\) dieser Zufallsvariable an.

      \(T_{Y}\) = {0, 1, 2}

    3. Geben Sie die Wahrscheinlichkeitsfunktion \(f\) von \(Y\) in Form einer Tabelle an.

      \(y\) 0 1 2
      \(f(y)\) \(\frac{2}{6}\) \(\frac{2}{6}\) \(\frac{2}{6}\)

    4. Geben Sie die Verteilungsfunktion \(F\) von \(Y\) in Form einer Tabelle an.

      \(y\) 0 1 2
      \(F(y)\) \(\frac{2}{6}\) \(\frac{4}{6}\) \(\frac{6}{6}\)

  1. Auf einer Kinomesse können Sie kostenlos an einem Gewinnspiel teilnehmen und einmal an einem Glücksrad drehen. Das Glücksrad bleibt auf einem Feld mit einer bestimmten Farbe stehen. Das Glücksrad besitzt Felder mit den Farben Türkis, Blau, Rot, Orange, Lila, Gelb und Grün.

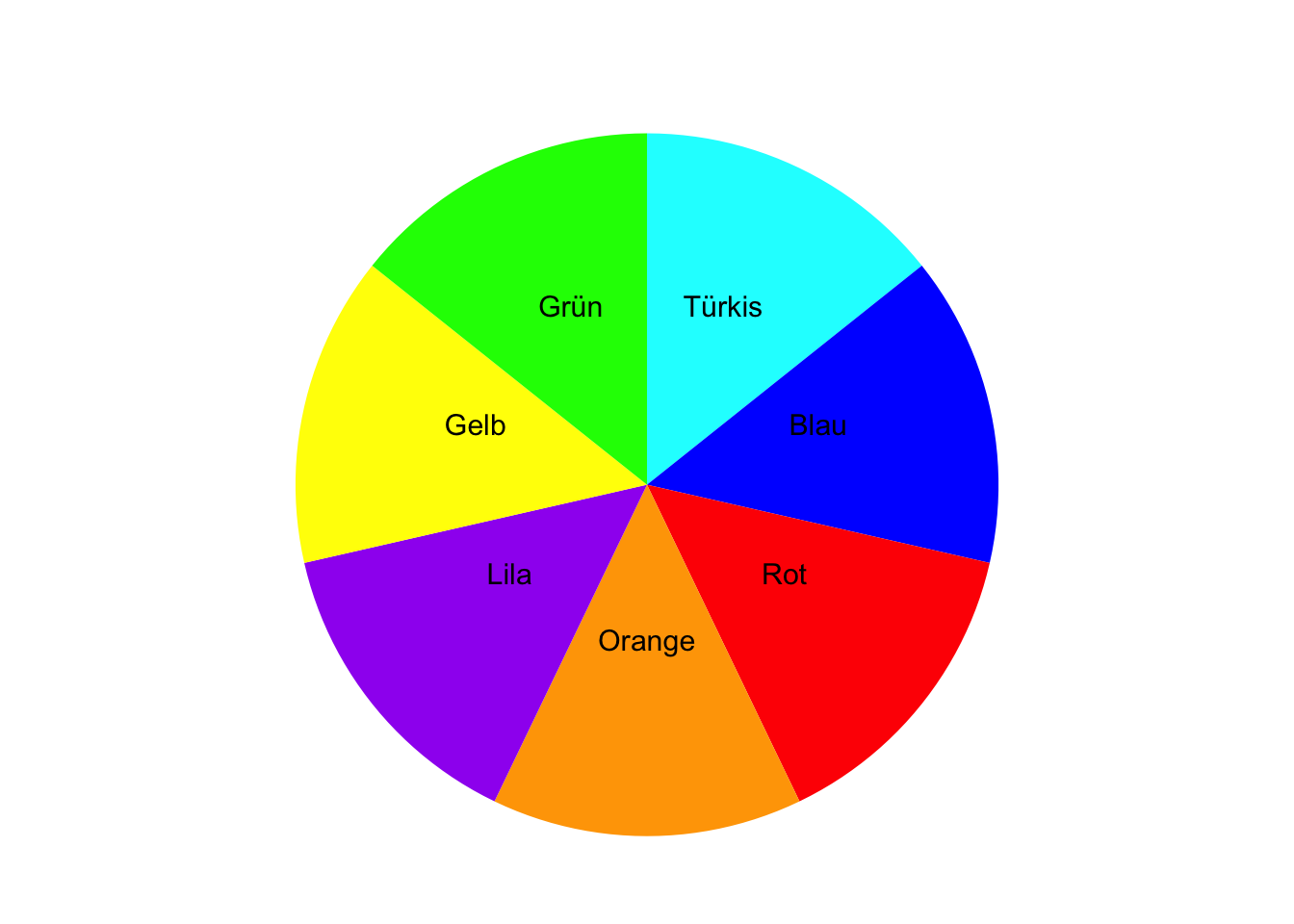
    1. Geben Sie die Ergebnismenge \(\Omega\) an.

      \(\Omega\) = {Türkis, Blau, Rot, Orange, Lila, Gelb, Grün}

    2. Geben Sie die Elementarereignisse an.

      Elementarereignisse sind: {Türkis}, {Blau}, {Rot}, {Orange}, {Lila}, {Gelb}, {Grün}

    3. Geben Sie die Wahrscheinlichkeit für die folgenden Ereignisse an. (Hinweis: Nehmen Sie an, dass alle Felder des Glücksrads gleich groß sind):

      1. \(A_1\): “Das Glücksrad bleibt auf dem Feld mit der Farbe Türkis stehen.”

        \(P(A_1) = P(\{Türkis\}) = \frac{1}{7}\)

      2. \(A_2\): “Das Glücksrad bleibt auf einem Feld mit der Farbe Gelb oder Orange stehen.”

        \(P(A_2) = P(\{Gelb, Orange\}) = P(\{Gelb\}) + P(\{Orange\}) = \frac{1}{7} + \frac{1}{7} = \frac{2}{7}\)

  2. Je nachdem auf welchem Feld das Glücksrad stehen bleibt, erhalten Sie einen Kino-Gutschein im Wert eines bestimmten Geldbetrags. Die Zufallsvariable \(X\) gibt den Wert des Gutscheins in Euro an, den Sie bei dem Gewinnspiel erhalten.

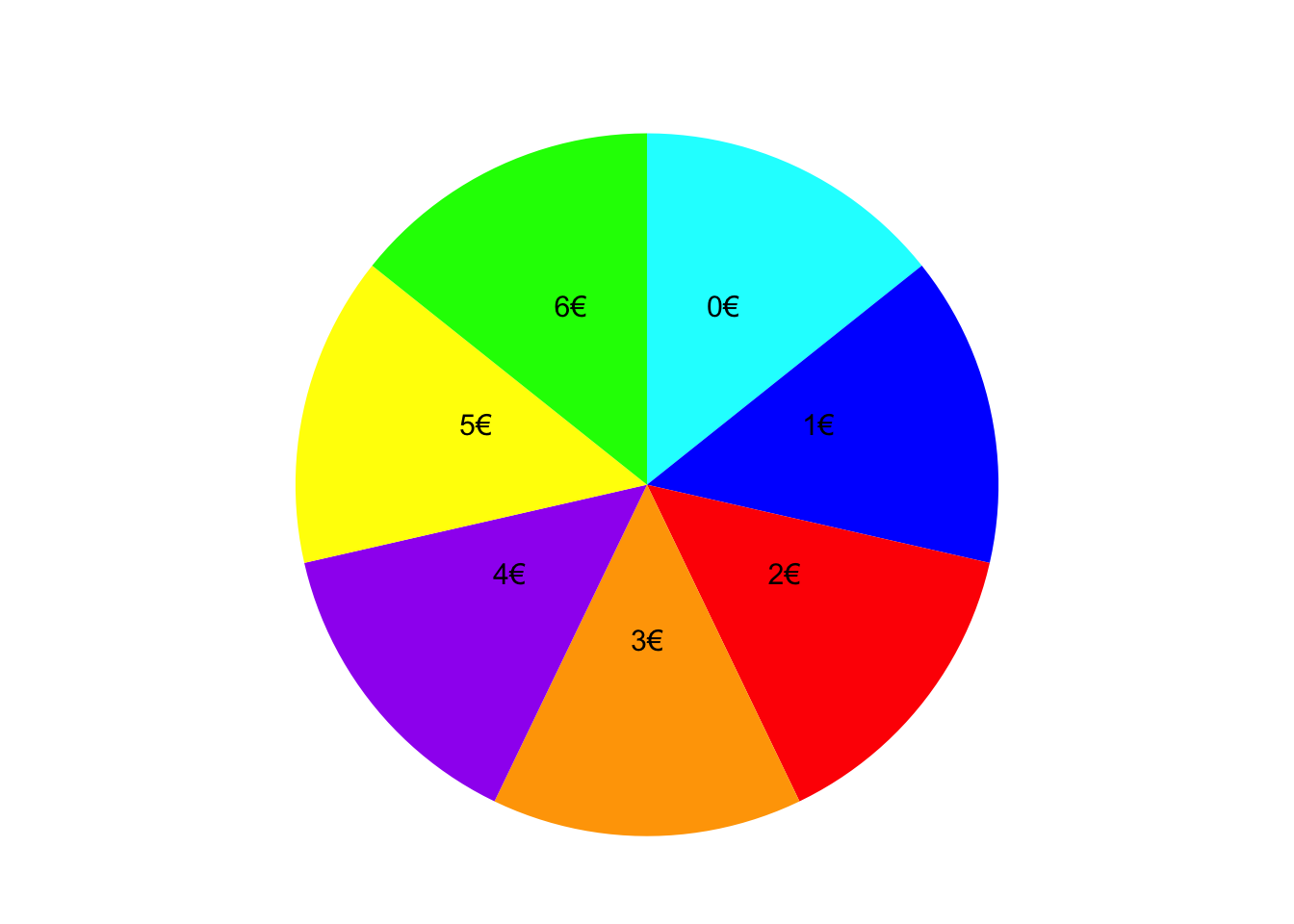
    1. Geben Sie den Träger der Zufallsvariable \(X\) an.

      \(T_{X}\) = {0, 1, 2, 3, 4, 5, 6}

    2. Geben Sie die Elementarereignisse der Zufallsvariable \(X\) an.

      Elementarereignisse sind: {0}, {1}, {2}, {3}, {4}, {5}, {6}

    3. Geben Sie die Wahrscheinlichkeit für die folgenden Ereignisse an. (Hinweis: Nehmen Sie an, dass alle Felder des Glücksrads gleich groß sind):

      1. \(A_{X1}\): “Sie erhalten einen Gutschein im Wert von mindestens 1 Euro.

        \(P_X(A_{X1}) = P_X(\{1,2,3,4,5,6\}) = P(\{Blau,Rot,Orange,Lila,Gelb,Grün\}) = \frac{6}{7} = 0.8571429\)

      2. \(A_{X2}\): “Sie erhalten einen Gutschein im Wert von weniger als 2 Euro.

        \(P_X(A_{X2}) = P_X(\{0,1\}) = P(\{Türkis,Blau\}) = \frac{2}{7} = 0.2857143\)

  3. Angenommen, eine Kinokarte kostet 1 Euro.

    1. Geben Sie in Form einer Tabelle eine Zufallsvariable \(Y\) an, die angibt, ob ihr Gutschein nach dem Gewinnspiel für keine (0), eine (1), oder zwei (2) Kinokarten ausreicht.

      \(\omega\) Türkis Blau Rot Orange Lila Gelb Grün
      x 0 1 2 3 4 5 6
      y 0 1 2 2 2 2 2

    2. Geben Sie den Träger \(T_{Y}\) dieser Zufallsvariable an.

      \(T_{Y}\) = {0, 1, 2}

    3. Geben Sie die Wahrscheinlichkeitsfunktion \(f\) von \(Y\) in Form einer Tabelle an.

      \(y\) 0 1 2
      \(f(y)\) \(\frac{1}{7}\) \(\frac{1}{7}\) \(\frac{5}{7}\)

    4. Geben Sie die Verteilungsfunktion \(F\) von \(Y\) in Form einer Tabelle an.

      \(y\) 0 1 2
      \(F(y)\) \(\frac{1}{7}\) \(\frac{2}{7}\) \(\frac{7}{7}\)

  1. Auf einer Kinomesse können Sie kostenlos an einem Gewinnspiel teilnehmen und einmal an einem Glücksrad drehen. Das Glücksrad bleibt auf einem Feld mit einer bestimmten Farbe stehen. Das Glücksrad besitzt Felder mit den Farben Grün, Rot, Orange, Türkis, Lila, Gelb und Blau.

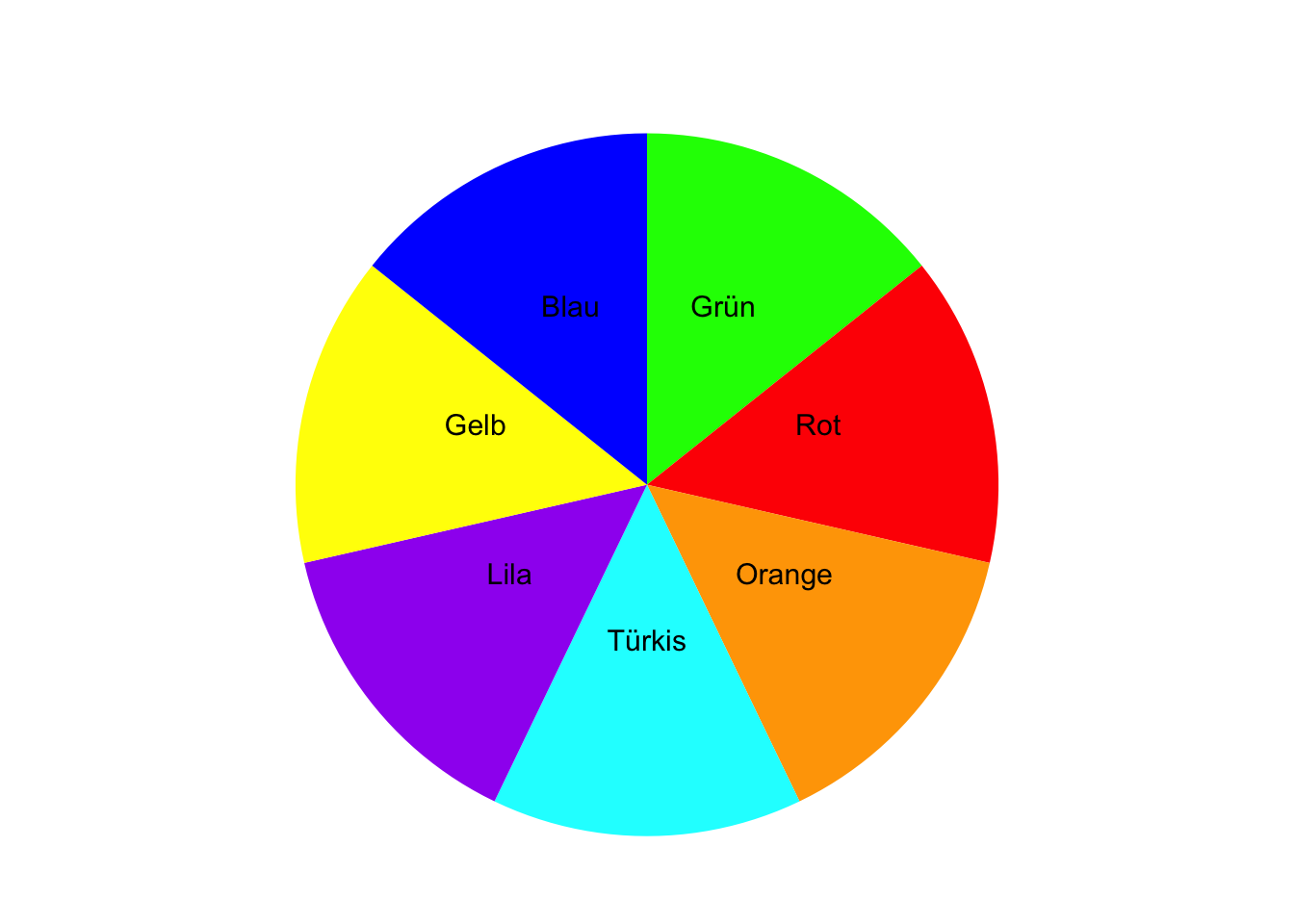
    1. Geben Sie die Ergebnismenge \(\Omega\) an.

      \(\Omega\) = {Grün, Rot, Orange, Türkis, Lila, Gelb, Blau}

    2. Geben Sie die Elementarereignisse an.

      Elementarereignisse sind: {Grün}, {Rot}, {Orange}, {Türkis}, {Lila}, {Gelb}, {Blau}

    3. Geben Sie die Wahrscheinlichkeit für die folgenden Ereignisse an. (Hinweis: Nehmen Sie an, dass alle Felder des Glücksrads gleich groß sind):

      1. \(A_1\): “Das Glücksrad bleibt auf dem Feld mit der Farbe Türkis stehen.”

        \(P(A_1) = P(\{Türkis\}) = \frac{1}{7}\)

      2. \(A_2\): “Das Glücksrad bleibt auf einem Feld mit der Farbe Grün oder Gelb stehen.”

        \(P(A_2) = P(\{Grün, Gelb\}) = P(\{Grün\}) + P(\{Gelb\}) = \frac{1}{7} + \frac{1}{7} = \frac{2}{7}\)

  2. Je nachdem auf welchem Feld das Glücksrad stehen bleibt, erhalten Sie einen Kino-Gutschein im Wert eines bestimmten Geldbetrags. Die Zufallsvariable \(X\) gibt den Wert des Gutscheins in Euro an, den Sie bei dem Gewinnspiel erhalten.

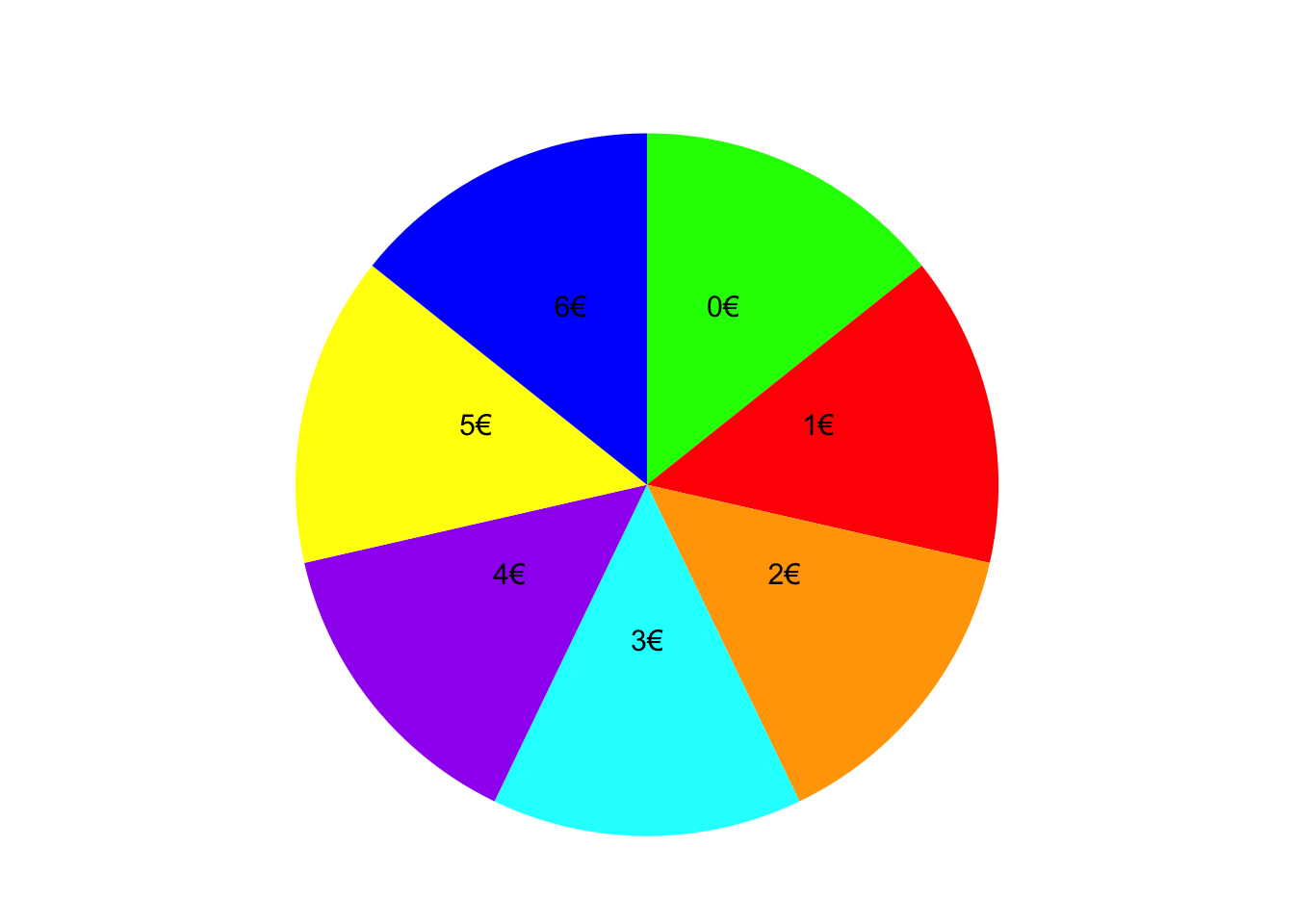
    1. Geben Sie den Träger der Zufallsvariable \(X\) an.

      \(T_{X}\) = {0, 1, 2, 3, 4, 5, 6}

    2. Geben Sie die Elementarereignisse der Zufallsvariable \(X\) an.

      Elementarereignisse sind: {0}, {1}, {2}, {3}, {4}, {5}, {6}

    3. Geben Sie die Wahrscheinlichkeit für die folgenden Ereignisse an. (Hinweis: Nehmen Sie an, dass alle Felder des Glücksrads gleich groß sind):

      1. \(A_{X1}\): “Sie erhalten einen Gutschein im Wert von mindestens 3 Euro.

        \(P_X(A_{X1}) = P_X(\{3,4,5,6\}) = P(\{Türkis,Lila,Gelb,Blau\}) = \frac{4}{7} = 0.5714286\)

      2. \(A_{X2}\): “Sie erhalten einen Gutschein im Wert von weniger als 4 Euro.

        \(P_X(A_{X2}) = P_X(\{0,1,2,3\}) = P(\{Grün,Rot,Orange,Türkis\}) = \frac{4}{7} = 0.5714286\)

  3. Angenommen, eine Kinokarte kostet 3 Euro.

    1. Geben Sie in Form einer Tabelle eine Zufallsvariable \(Y\) an, die angibt, ob ihr Gutschein nach dem Gewinnspiel für keine (0), eine (1), oder zwei (2) Kinokarten ausreicht.

      \(\omega\) Grün Rot Orange Türkis Lila Gelb Blau
      x 0 1 2 3 4 5 6
      y 0 0 0 1 1 1 2

    2. Geben Sie den Träger \(T_{Y}\) dieser Zufallsvariable an.

      \(T_{Y}\) = {0, 1, 2}

    3. Geben Sie die Wahrscheinlichkeitsfunktion \(f\) von \(Y\) in Form einer Tabelle an.

      \(y\) 0 1 2
      \(f(y)\) \(\frac{3}{7}\) \(\frac{3}{7}\) \(\frac{1}{7}\)

    4. Geben Sie die Verteilungsfunktion \(F\) von \(Y\) in Form einer Tabelle an.

      \(y\) 0 1 2
      \(F(y)\) \(\frac{3}{7}\) \(\frac{6}{7}\) \(\frac{7}{7}\)

  1. Auf einer Kinomesse können Sie kostenlos an einem Gewinnspiel teilnehmen und einmal an einem Glücksrad drehen. Das Glücksrad bleibt auf einem Feld mit einer bestimmten Farbe stehen. Das Glücksrad besitzt Felder mit den Farben Grün, Gelb, Orange, Türkis, Lila, Rot und Blau.

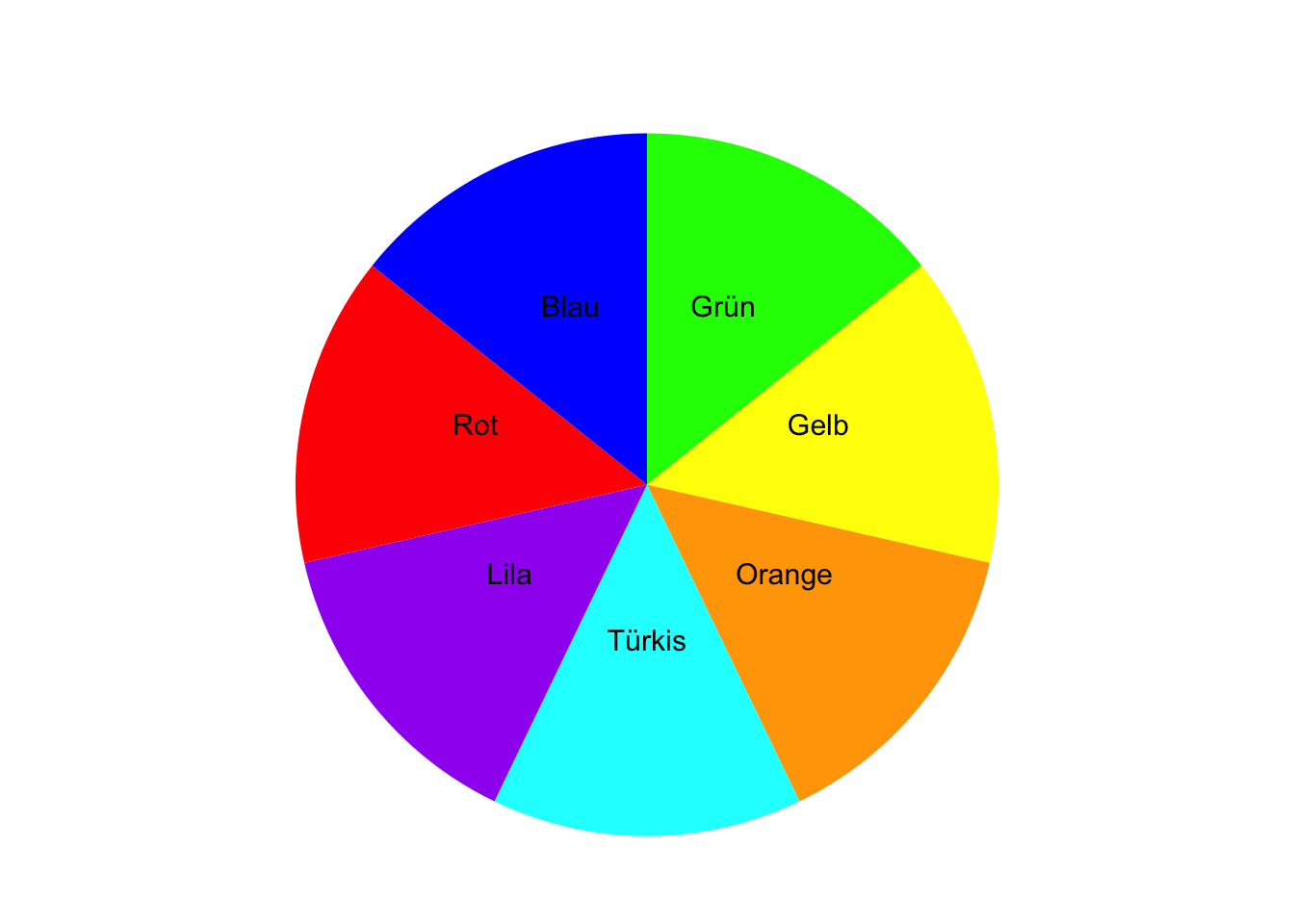
    1. Geben Sie die Ergebnismenge \(\Omega\) an.

      \(\Omega\) = {Grün, Gelb, Orange, Türkis, Lila, Rot, Blau}

    2. Geben Sie die Elementarereignisse an.

      Elementarereignisse sind: {Grün}, {Gelb}, {Orange}, {Türkis}, {Lila}, {Rot}, {Blau}

    3. Geben Sie die Wahrscheinlichkeit für die folgenden Ereignisse an. (Hinweis: Nehmen Sie an, dass alle Felder des Glücksrads gleich groß sind):

      1. \(A_1\): “Das Glücksrad bleibt auf dem Feld mit der Farbe Orange stehen.”

        \(P(A_1) = P(\{Orange\}) = \frac{1}{7}\)

      2. \(A_2\): “Das Glücksrad bleibt auf einem Feld mit der Farbe Lila oder Gelb stehen.”

        \(P(A_2) = P(\{Lila, Gelb\}) = P(\{Lila\}) + P(\{Gelb\}) = \frac{1}{7} + \frac{1}{7} = \frac{2}{7}\)

  2. Je nachdem auf welchem Feld das Glücksrad stehen bleibt, erhalten Sie einen Kino-Gutschein im Wert eines bestimmten Geldbetrags. Die Zufallsvariable \(X\) gibt den Wert des Gutscheins in Euro an, den Sie bei dem Gewinnspiel erhalten.

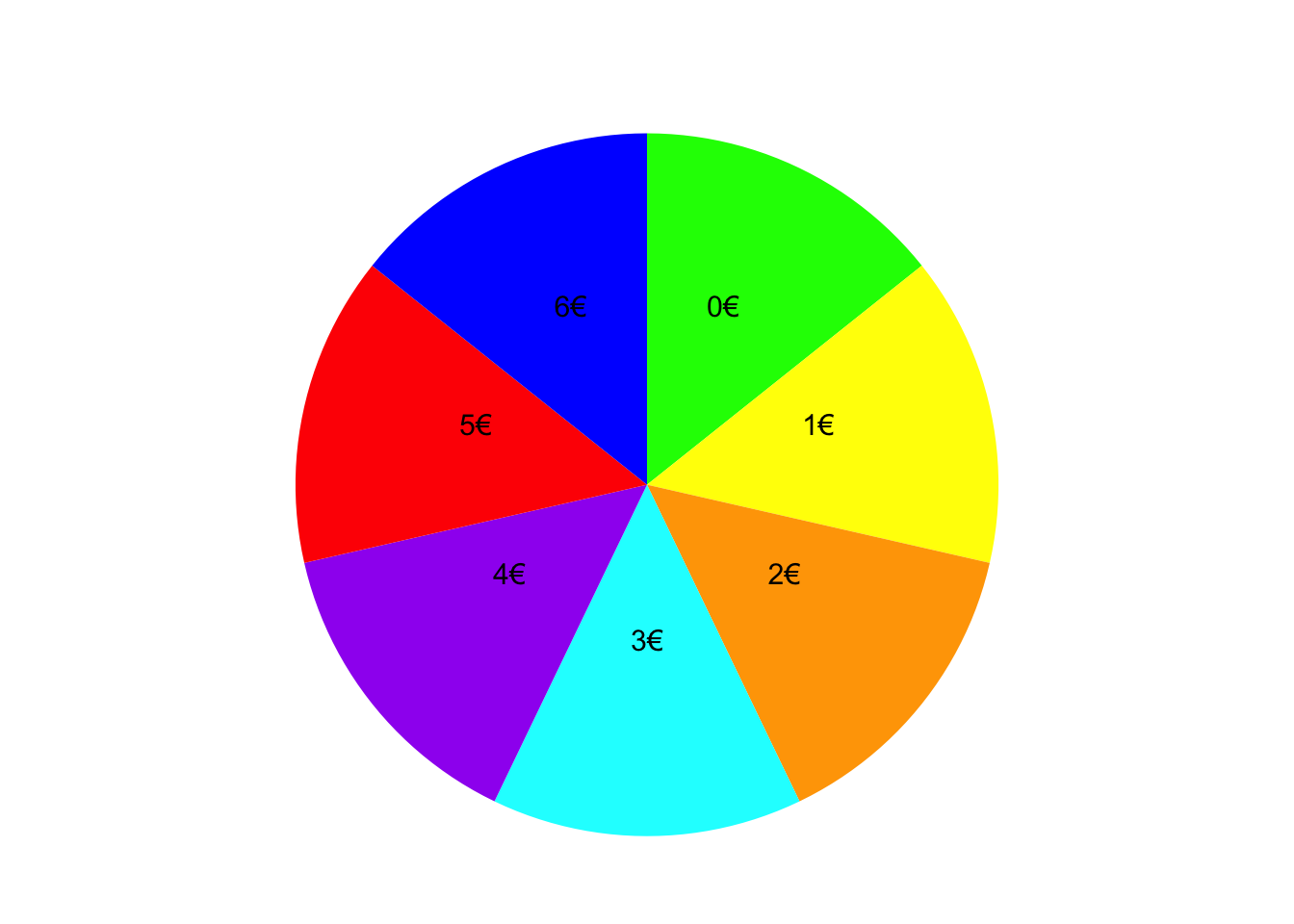
    1. Geben Sie den Träger der Zufallsvariable \(X\) an.

      \(T_{X}\) = {0, 1, 2, 3, 4, 5, 6}

    2. Geben Sie die Elementarereignisse der Zufallsvariable \(X\) an.

      Elementarereignisse sind: {0}, {1}, {2}, {3}, {4}, {5}, {6}

    3. Geben Sie die Wahrscheinlichkeit für die folgenden Ereignisse an. (Hinweis: Nehmen Sie an, dass alle Felder des Glücksrads gleich groß sind):

      1. \(A_{X1}\): “Sie erhalten einen Gutschein im Wert von mindestens 1 Euro.

        \(P_X(A_{X1}) = P_X(\{1,2,3,4,5,6\}) = P(\{Gelb,Orange,Türkis,Lila,Rot,Blau\}) = \frac{6}{7} = 0.8571429\)

      2. \(A_{X2}\): “Sie erhalten einen Gutschein im Wert von weniger als 3 Euro.

        \(P_X(A_{X2}) = P_X(\{0,1,2\}) = P(\{Grün,Gelb,Orange\}) = \frac{3}{7} = 0.4285714\)

  3. Angenommen, eine Kinokarte kostet 3 Euro.

    1. Geben Sie in Form einer Tabelle eine Zufallsvariable \(Y\) an, die angibt, ob ihr Gutschein nach dem Gewinnspiel für keine (0), eine (1), oder zwei (2) Kinokarten ausreicht.

      \(\omega\) Grün Gelb Orange Türkis Lila Rot Blau
      x 0 1 2 3 4 5 6
      y 0 0 0 1 1 1 2

    2. Geben Sie den Träger \(T_{Y}\) dieser Zufallsvariable an.

      \(T_{Y}\) = {0, 1, 2}

    3. Geben Sie die Wahrscheinlichkeitsfunktion \(f\) von \(Y\) in Form einer Tabelle an.

      \(y\) 0 1 2
      \(f(y)\) \(\frac{3}{7}\) \(\frac{3}{7}\) \(\frac{1}{7}\)

    4. Geben Sie die Verteilungsfunktion \(F\) von \(Y\) in Form einer Tabelle an.

      \(y\) 0 1 2
      \(F(y)\) \(\frac{3}{7}\) \(\frac{6}{7}\) \(\frac{7}{7}\)

  1. Auf einer Kinomesse können Sie kostenlos an einem Gewinnspiel teilnehmen und einmal an einem Glücksrad drehen. Das Glücksrad bleibt auf einem Feld mit einer bestimmten Farbe stehen. Das Glücksrad besitzt Felder mit den Farben Blau, Rot und Orange.

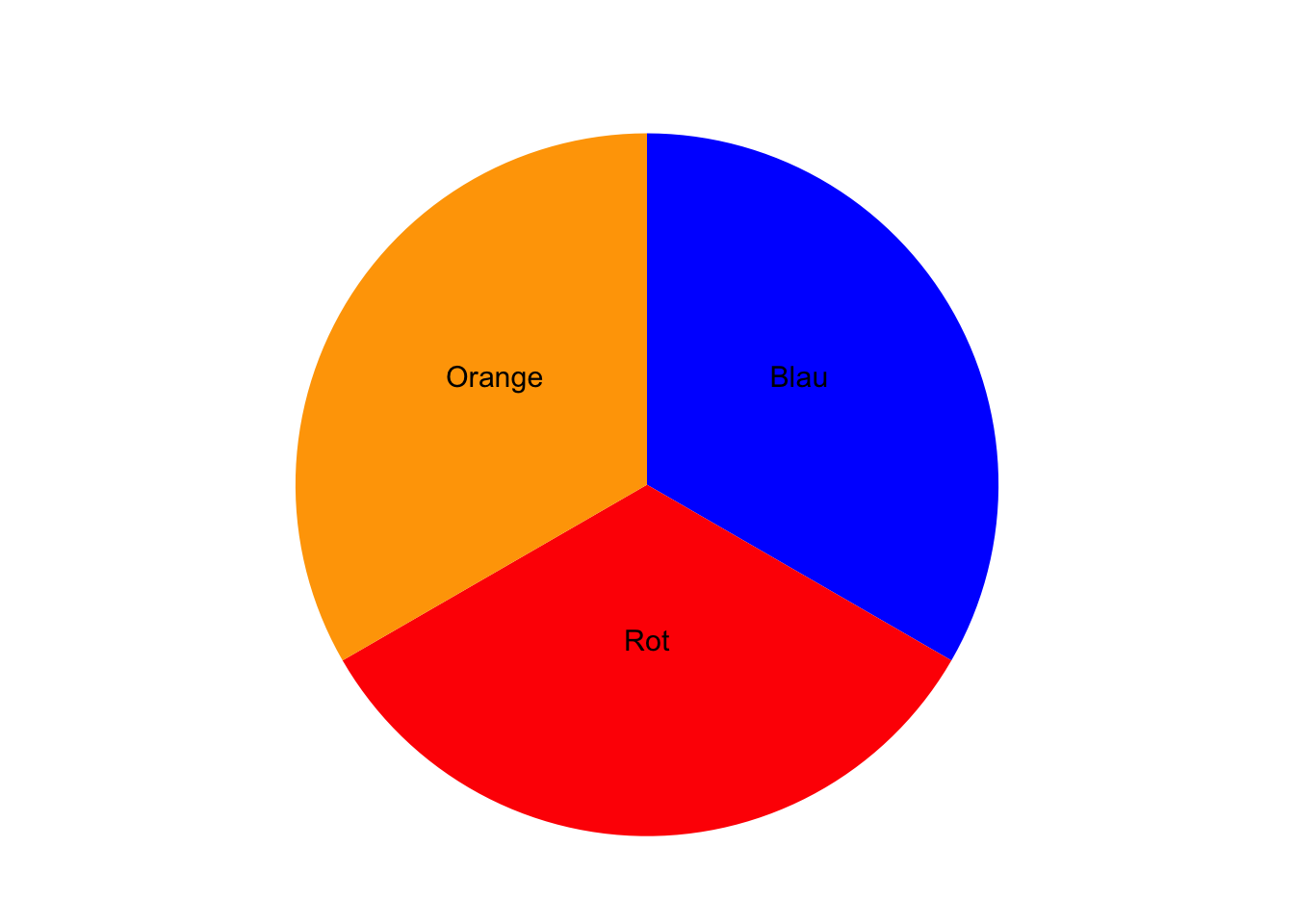
    1. Geben Sie die Ergebnismenge \(\Omega\) an.

      \(\Omega\) = {Blau, Rot, Orange}

    2. Geben Sie die Elementarereignisse an.

      Elementarereignisse sind: {Blau}, {Rot}, {Orange}

    3. Geben Sie die Wahrscheinlichkeit für die folgenden Ereignisse an. (Hinweis: Nehmen Sie an, dass alle Felder des Glücksrads gleich groß sind):

      1. \(A_1\): “Das Glücksrad bleibt auf dem Feld mit der Farbe Orange stehen.”

        \(P(A_1) = P(\{Orange\}) = \frac{1}{3}\)

      2. \(A_2\): “Das Glücksrad bleibt auf einem Feld mit der Farbe Blau oder Rot stehen.”

        \(P(A_2) = P(\{Blau, Rot\}) = P(\{Blau\}) + P(\{Rot\}) = \frac{1}{3} + \frac{1}{3} = \frac{2}{3}\)

  2. Je nachdem auf welchem Feld das Glücksrad stehen bleibt, erhalten Sie einen Kino-Gutschein im Wert eines bestimmten Geldbetrags. Die Zufallsvariable \(X\) gibt den Wert des Gutscheins in Euro an, den Sie bei dem Gewinnspiel erhalten.

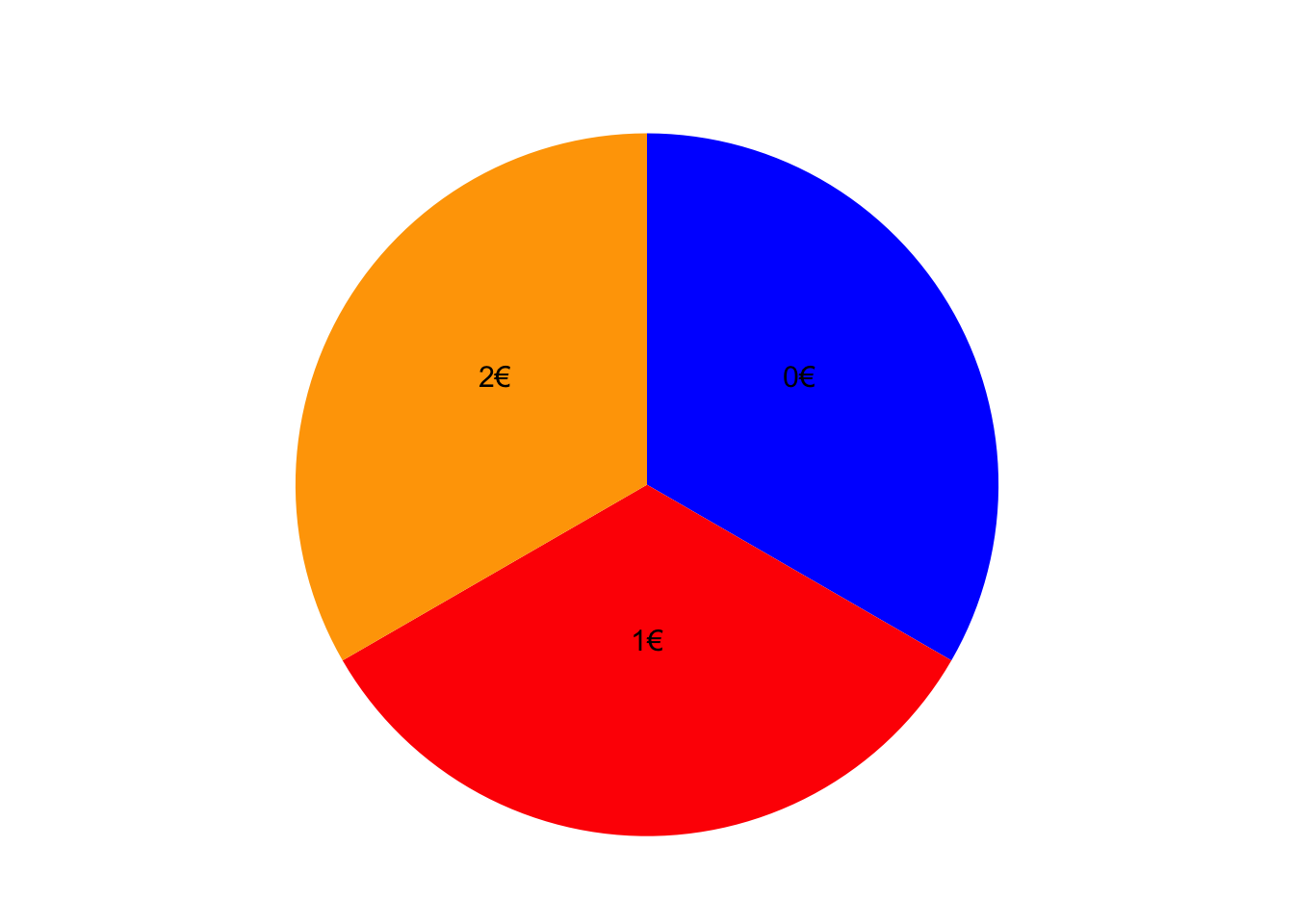
    1. Geben Sie den Träger der Zufallsvariable \(X\) an.

      \(T_{X}\) = {0, 1, 2}

    2. Geben Sie die Elementarereignisse der Zufallsvariable \(X\) an.

      Elementarereignisse sind: {0}, {1}, {2}

    3. Geben Sie die Wahrscheinlichkeit für die folgenden Ereignisse an. (Hinweis: Nehmen Sie an, dass alle Felder des Glücksrads gleich groß sind):

      1. \(A_{X1}\): “Sie erhalten einen Gutschein im Wert von mindestens 2 Euro.

        \(P_X(A_{X1}) = P_X(\{2\}) = P(\{Orange\}) = \frac{1}{3} = 0.3333333\)

      2. \(A_{X2}\): “Sie erhalten einen Gutschein im Wert von weniger als 2 Euro.

        \(P_X(A_{X2}) = P_X(\{0,1\}) = P(\{Blau,Rot\}) = \frac{2}{3} = 0.6666667\)

  3. Angenommen, eine Kinokarte kostet 3 Euro.

    1. Geben Sie in Form einer Tabelle eine Zufallsvariable \(Y\) an, die angibt, ob ihr Gutschein nach dem Gewinnspiel für keine (0), eine (1), oder zwei (2) Kinokarten ausreicht.

      \(\omega\) Blau Rot Orange
      x 0 1 2
      y 0 0 0

    2. Geben Sie den Träger \(T_{Y}\) dieser Zufallsvariable an.

      \(T_{Y}\) = {0}

    3. Geben Sie die Wahrscheinlichkeitsfunktion \(f\) von \(Y\) in Form einer Tabelle an.

      \(y\) 0
      \(f(y)\) \(\frac{3}{3}\)

    4. Geben Sie die Verteilungsfunktion \(F\) von \(Y\) in Form einer Tabelle an.

      \(y\) 0
      \(F(y)\) \(\frac{3}{3}\)

  1. Auf einer Kinomesse können Sie kostenlos an einem Gewinnspiel teilnehmen und einmal an einem Glücksrad drehen. Das Glücksrad bleibt auf einem Feld mit einer bestimmten Farbe stehen. Das Glücksrad besitzt Felder mit den Farben Türkis und Blau.

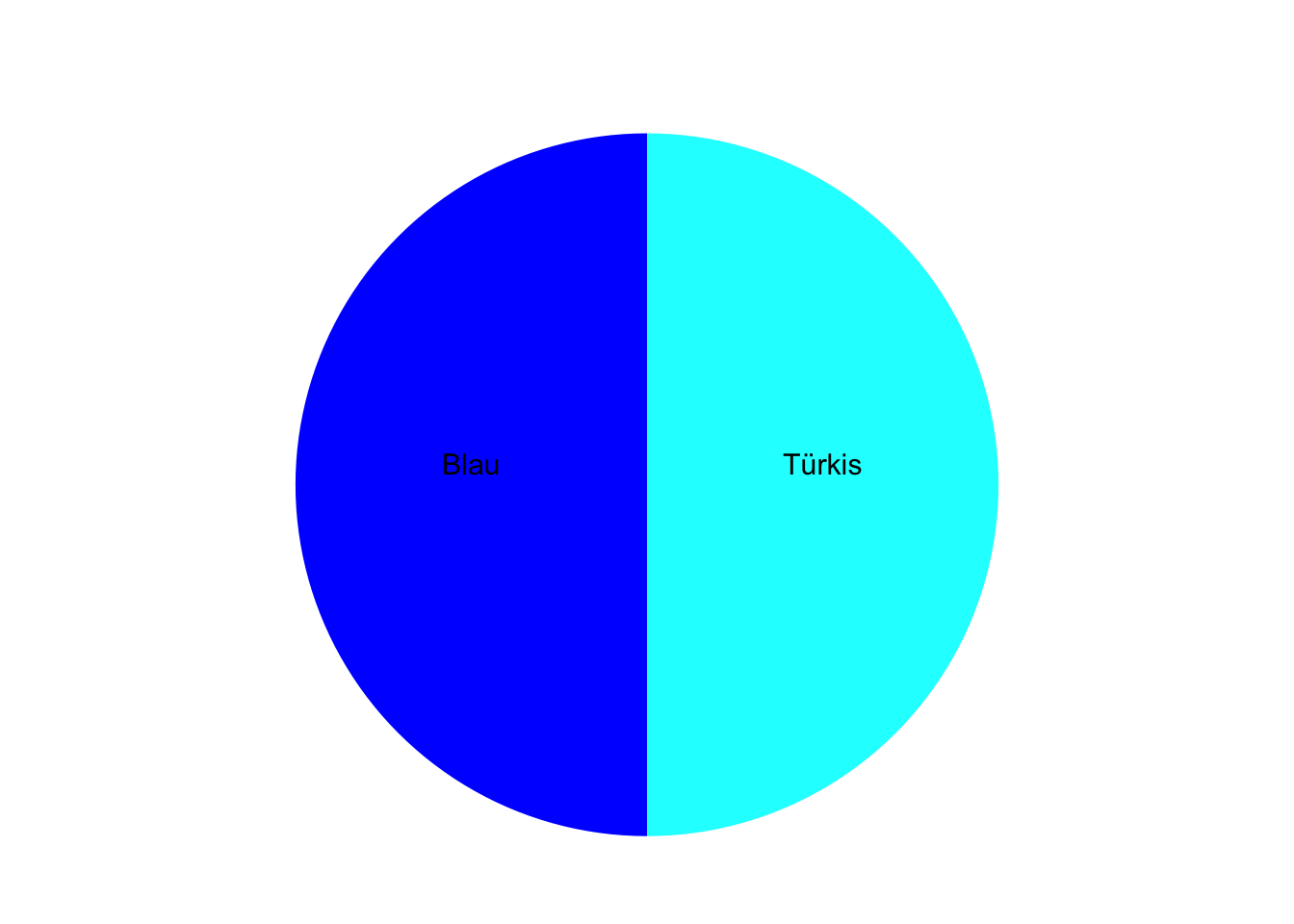
    1. Geben Sie die Ergebnismenge \(\Omega\) an.

      \(\Omega\) = {Türkis, Blau}

    2. Geben Sie die Elementarereignisse an.

      Elementarereignisse sind: {Türkis}, {Blau}

    3. Geben Sie die Wahrscheinlichkeit für die folgenden Ereignisse an. (Hinweis: Nehmen Sie an, dass alle Felder des Glücksrads gleich groß sind):

      1. \(A_1\): “Das Glücksrad bleibt auf dem Feld mit der Farbe Blau stehen.”

        \(P(A_1) = P(\{Blau\}) = \frac{1}{2}\)

      2. \(A_2\): “Das Glücksrad bleibt auf einem Feld mit der Farbe Blau oder Türkis stehen.”

        \(P(A_2) = P(\{Blau, Türkis\}) = P(\{Blau\}) + P(\{Türkis\}) = \frac{1}{2} + \frac{1}{2} = \frac{2}{2}\)

  2. Je nachdem auf welchem Feld das Glücksrad stehen bleibt, erhalten Sie einen Kino-Gutschein im Wert eines bestimmten Geldbetrags. Die Zufallsvariable \(X\) gibt den Wert des Gutscheins in Euro an, den Sie bei dem Gewinnspiel erhalten.

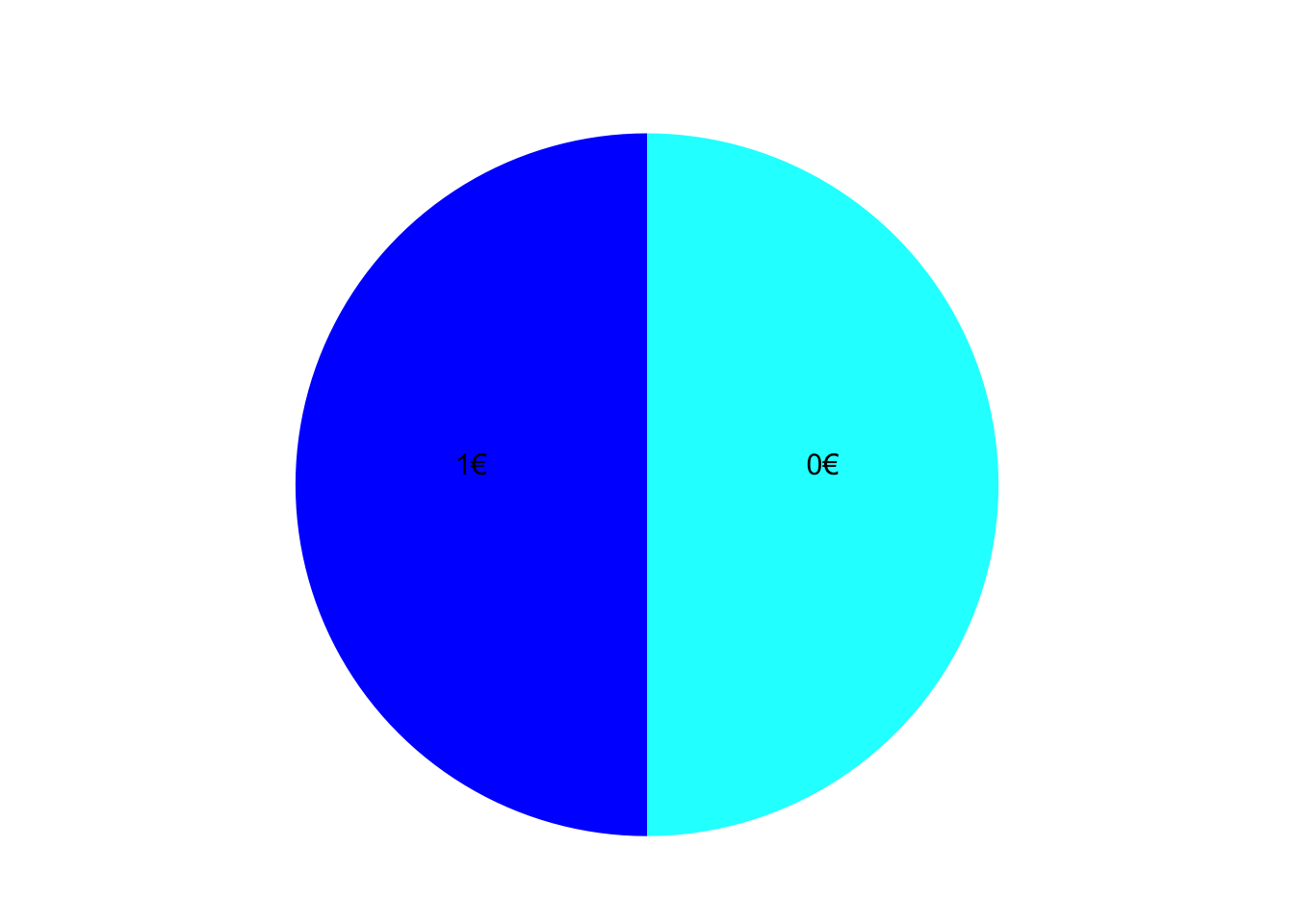
    1. Geben Sie den Träger der Zufallsvariable \(X\) an.

      \(T_{X}\) = {0, 1}

    2. Geben Sie die Elementarereignisse der Zufallsvariable \(X\) an.

      Elementarereignisse sind: {0}, {1}

    3. Geben Sie die Wahrscheinlichkeit für die folgenden Ereignisse an. (Hinweis: Nehmen Sie an, dass alle Felder des Glücksrads gleich groß sind):

      1. \(A_{X1}\): “Sie erhalten einen Gutschein im Wert von mindestens 1 Euro.

        \(P_X(A_{X1}) = P_X(\{1\}) = P(\{Blau\}) = \frac{1}{2} = 0.5\)

      2. \(A_{X2}\): “Sie erhalten einen Gutschein im Wert von weniger als 1 Euro.

        \(P_X(A_{X2}) = P_X(\{0\}) = P(\{Türkis\}) = \frac{1}{2} = 0.5\)

  3. Angenommen, eine Kinokarte kostet 2 Euro.

    1. Geben Sie in Form einer Tabelle eine Zufallsvariable \(Y\) an, die angibt, ob ihr Gutschein nach dem Gewinnspiel für keine (0), eine (1), oder zwei (2) Kinokarten ausreicht.

      \(\omega\) Türkis Blau
      x 0 1
      y 0 0

    2. Geben Sie den Träger \(T_{Y}\) dieser Zufallsvariable an.

      \(T_{Y}\) = {0}

    3. Geben Sie die Wahrscheinlichkeitsfunktion \(f\) von \(Y\) in Form einer Tabelle an.

      \(y\) 0
      \(f(y)\) \(\frac{2}{2}\)

    4. Geben Sie die Verteilungsfunktion \(F\) von \(Y\) in Form einer Tabelle an.

      \(y\) 0
      \(F(y)\) \(\frac{2}{2}\)