Übungsaufgaben

Normalverteilung, einfache Zufallsstichprobe, Schätzfunktionen und Schätzgütekriterien

Hinweis

Die hier veröffentlichten Übungsaufgaben sind brandneu und deshalb noch nicht auf Herz und Nieren überprüft. Sollten Sie Fehler entdecken, geben Sie uns bitte unbedingt eine Rückmeldung an philipp.sckopke(at)psy.lmu.de, damit wir so bald wie möglich eine verbesserte Version online stellen können.

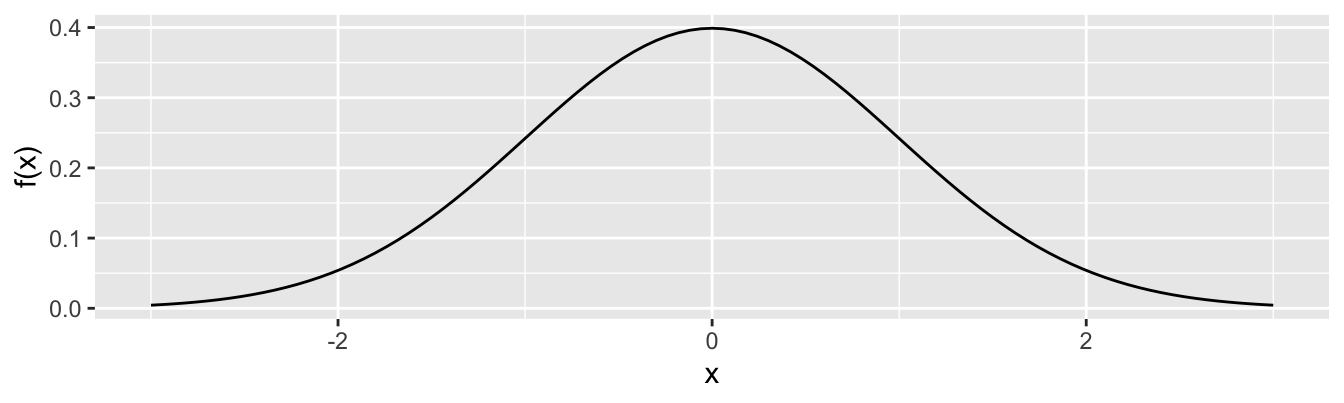
  1. Sei \(X\) eine stetige, standardnormalverteilte Zufallsvariable mit Träger \(T_{X}\mathbb{= R}\) und Wahrscheinlichkeitsdichtefunktion1:

    \(f(x) = \frac{1}{\sqrt{2\pi}}\exp\left( - \frac{x^{2}}{2} \right)\)

    Mit der Funktion pnorm(x) können Sie in R Funktionswerte \(F(x)\) der Verteilungsfunktion von (standard-)normalverteilten Zufallsvariablen berechnen. Sie erhalten für einige Werte von \(x\) die folgenden R-Outputs:

    pnorm(-2)
    [1] 0.02275013


    pnorm(0)
    [1] 0.5


    pnorm(1)
    [1] 0.8413447

    Berechnen Sie die folgenden rot markierten Flächen unter der Wahrscheinlichkeitsdichtefunktion ausschließlich mit Hilfe der angegebenen Funktionswerte. Welche Wahrscheinlichkeiten berechnen Sie mit diesen Flächen?

    1. Mit der Fläche unter der Kurve berechnen wir die Wahrscheinlichkeit, dass die Zufallsvariable \(X\) einen Wert kleiner \(-2\) annimmt. Hier hilft pnorm(-2) weiter, denn:

      \(P(X \leq -2) = F(-2) =\) pnorm(-2) \(\approx 0.023\)

    2. Mit der Fläche unter der Kurve berechnen wir die Wahrscheinlichkeit, dass die Zufallsvariable \(X\) einen Wert größer \(1\) annimmt. Hier hilft pnorm(1) weiter, sowie die Eigenschaft, dass die gesamte Fläche unter jeder Wahrscheinlichkeitsdichtefunktion immer \(1\) ist:

      \(P(X > 1) = 1 - P(X \leq 1) = 1 - F(1) =\) 1 - pnorm(1) \(\approx 0.159\)

    3. Mit der Fläche unter der Kurve berechnen wir die Wahrscheinlichkeit, dass die Zufallsvariable \(X\) einen Wert zwischen \(-2\) und \(2\) annimmt. Hierfür bräuchten wir pnorm(-2), allerdings auch pnorm(2), das oben aber nicht angegeben ist. Glücklicherweise ist die Dichtefunktion um den Wert \(x =0\) symmetrisch. Wir können pnorm(2) also relativ einfach aus pnorm(-2) berechnen:

      \(F(2) =\) pnorm(2) = 1 - pnorm(-2) \(= 0.9772499\)

      Damit können wir die Fläche berechnen:

      \[\begin{align*} P(|X| < 2) &= P(X \leq 2) - P(X \leq -2) \\ &= F(2) - F(-2) \\ &= pnorm(2) - pnorm(-2) \\ &= 1 - pnorm(-2) - pnorm(-2) \\ &= 1 - 0.0227501 - 0.0227501 \\ &\approx 0.954 \end{align*}\]

    4. Mit der Fläche unter der Kurve berechnen wir die Wahrscheinlichkeit, dass die Zufallsvariable \(X\) einen Wert kleiner \(-1\) oder größer \(1\) annimmt. Um die Größe der rechten der beiden Flächen zu ermitteln, verwenden wir pnorm(1):

      \(P(X > 1) = 1 - P(X \leq 1) = 1 - F(1) = 1 - 0.8413447 \approx 0.159\)

      So wie oben machen wir uns zu Nutze, dass die Dichtefunktion symmetrisch ist und verdoppeln diesen Wert:

      \(P(|X| \geq 1) = 2 \cdot (1 - F(1)) = 2 \cdot 0.159 \approx 0.318\)

  1. Sei X eine stetige Zufallsvariable, die für die Körpergröße einer zufällig gezogenen Person steht. Gehen Sie davon aus, dass \(X\) normalverteilt ist mit \(\mu = 170\) und \(\sigma^{2} = 36\). Beantworten Sie die folgenden Fragen mit Hilfe der R-Funktion pnorm().

    1. Wie hoch ist die Wahrscheinlichkeit, dass die zufällig gezogene Person eine Körpergröße von mehr als 188 hat?

      1 - pnorm(188, mean = 170, sd = 6)
      [1] 0.001349898

    2. Wie hoch ist die Wahrscheinlichkeit, dass die zufällig gezogene Person eine Körpergröße von weniger als 161 hat?

      pnorm(161, mean = 170, sd = 6)
      [1] 0.0668072

    3. Wie hoch ist die Wahrscheinlichkeit, dass die zufällig gezogene Person eine Körpergröße zwischen 188 und 161 hat?

      pnorm(188, mean = 170, sd = 6) - pnorm(161, mean = 170, sd = 6)
      [1] 0.9318429

    4. Wie hoch ist die Wahrscheinlichkeit, dass die zufällig gezogene Person eine extreme Körpergröße (mehr als 2 Standardabweichungen unter oder über dem Mittelwert) aufweist?

      1 - pnorm(182, mean = 170, sd = 6) + pnorm(158, mean = 170, sd = 6)
      [1] 0.04550026

      Oder

      2 * pnorm(158, mean = 170, sd = 6)
      [1] 0.04550026

      da die Normalverteilung symmetrisch ist.

      Statt beide Wahrscheinlichkeiten separat zu berechnen und zu addieren, kann diese Symmetrie ausgenutzt werden. Daher genügt es, die Wahrscheinlichkeit zu berechnen, dass eine Person extrem klein ist (also mehr als 2 Standardabweichungen unter dem Mittelwert liegt), und das Ergebnis einfach zu verdoppeln, um die Gesamtwahrscheinlichkeit für extreme Körpergrößen (über und unter dem Mittelwert) zu erhalten.

  1. Sie interessieren sich für die relative Häufigkeit von Depressionen in Deutschland. Sie ziehen zufällig und unabhängig voneinander n Person aus der Population, wobei jedoch alle Personen, die keine Studentinnen sind, eine Wahrscheinlichkeit von Null haben, in die Stichprobe gezogen zu werden. Alle Studentinnen haben die gleiche (positive) Wahrscheinlichkeit gezogen zu werden. Sie betrachten die Zufallsvariablen \(X_{1}\), \(X_{2}\), …, \(X_{i}\), …, \(X_{n}\), die jeweils den Wert 1 annehmen, falls die zufällig gezogene Person i unter einer Depression leidet, und den Wert 0, falls nicht.

    1. Welcher Wahrscheinlichkeitsverteilung folgen die Zufallsvariablen \(X_{1}\), \(X_{2}\), …, \(X_{i}\), …, \(X_{n}\) jeweils?

      Die Stichprobe ist immer noch eine einfache Zufallsstichprobe, jedoch nur aus der Teilpopulation der Studentinnen. Für die Zufallsvariablen gilt: \(X_{i}\ \sim\ Be(\pi)\) für alle i = 1, 2, …, n

    2. Welcher deskriptivstatistischen Maßzahl in welcher Population entspricht der Parameter dieser Verteilung?

      Der relativen Häufigkeit der Depressionen bei Studentinnen.

    3. Welches Problem liegt hier bei der Stichprobenziehung vor?

      Fehlende Repräsentativität.

  1. Sie betrachten eine Population, die aus den Personen Anna, Ella, Mia, Paul, Emil, Emre besteht. Sie ziehen eine einfache Zufallsstichprobe der Größe n = 3 aus dieser Population.

    1. Geben Sie zwei mögliche Ergebnisse dieses Zufallsexperiments an.

      Zum Beispiel:

      Mia, Emre, Mia

      oder:

      Anna, Ella, Mia

    2. Seien \(X_{1}\), \(X_{2}\), \(X_{3}\) Zufallsvariablen, die jeweils den Wert 1 annehmen, falls der Name der ersten, zweiten, dritten gezogenen Person mit E beginnt. Welcher Wahrscheinlichkeitsverteilung folgen die Zufallsvariablen?

      \(X_{i}\ \sim\ Be(\frac{1}{2})\) für alle i = 1, 2, 3

    3. Welcher deskriptivstatistischen Maßzahl in der Population entspricht der Parameter dieser Verteilung?

      Der relativen Häufigkeit von Personen, deren Namen mit E beginnt in der Population.

    4. Sie betrachten die Schätzfunktion \(\overline{X}\) für den Parameter der Wahrscheinlichkeitsverteilung von \(X_{1}\), \(X_{2}\), \(X_{3}\). Geben Sie den Träger von \(\overline{X}\) an.

      \[T_{\overline{X}} = \left\{ 0, \frac{1}{3}, \frac{2}{3}, \ 1 \right\}\]

    5. Berechnen Sie den Erwartungswert von \(\overline{X}\). Interpretieren Sie diesen.

      \[E\left( \overline{X} \right) = \pi = \frac{1}{2}\]

      Falls man unendlich oft eine Stichprobe der Größe n = 3 aus der Population ziehen würde und jedes Mal den Schätzwert \(\overline{x}\) in der gezogenen Stichprobe berechnen würde, wäre der Mittelwert aller dieser Schätzwerte \(\frac{1}{2}\), würde also dem wahren Parameterwert \(\pi = \frac{1}{2}\) entsprechen.

    6. Berechnen Sie den Standardfehler von \(\overline{X}\). Interpretieren Sie diesen.

      \[SE\left( \overline{X} \right) = \sqrt{\frac{\pi(1 - \pi)}{n}} = \sqrt{\frac{0.5(1 - 0.5)}{3}} \approx 0.289\]

      Falls man unendlich oft eine Stichprobe der Größe n = 3 aus der Population ziehen würde und jedes Mal den Schätzwert \(\overline{x}\) in der gezogenen Stichprobe berechnen würde, wäre die empirische Standardabweichung aller dieser Schätzwerte 0.289.

  1. Gesucht ist der Anteil der Personen in Deutschland, bei denen im letzten Jahr eine Depression diagnostiziert wurde.

    1. Ihnen liegt eine einfache Zufallsstichprobe mit Umfang n = 560 vor. Nennen Sie eine geeignete Schätzfunktion für die relative Häufigkeit der Personen in Deutschland, bei denen im letzten Jahr eine Depression diagnostiziert wurde.

      Der Mittelwert von Bernoulli-Variablen entspricht der relativen Häufigkeit. Ein geeigneter Schätzer für die relative Häufigkeit für die Variable Depression in Deutschland wäre daher:

      \[\overline{X} = \frac{1}{n}\sum_{i = 1}^{n}X_{i}\]

    2. Geben Sie den Standardfehler dieser Schätzfunktion an.

      \[SE\left( \overline{X} \right) = \sqrt{\frac{\pi(1 - \pi)}{n}} = \sqrt{\frac{\pi(1 - \pi)}{560}}\]

    3. Bei 255 Personen in Ihrer Stichprobe wurde im letzten Jahr eine Depression diagnostiziert. Bestimmen Sie den Schätzwert und interpretieren Sie ihn.

      \[\overline{x} = h(1) = \frac{255}{560} \approx 0.455\]

      Auf Basis der Stichprobe wird der Anteil Deutscher, bei denen im letzten Jahr eine Depression diagnostiziert wurde, auf 45.5 % geschätzt.

  1. Sei X eine stetige Zufallsvariable, die für die Schuhgröße einer zufällig gezogenen Person steht. Gehen Sie davon aus, dass \(X\) normalverteilt ist mit \(\mu = 40\) und \(\sigma^{2} = 4\). Beantworten Sie die folgenden Fragen mit Hilfe der R-Funktion pnorm().

    1. Wie hoch ist die Wahrscheinlichkeit, dass die zufällig gezogene Person eine Schuhgröße von mehr als 45 hat?

      1 - pnorm(45, mean = 40, sd = 2)
      [1] 0.006209665

    2. Wie hoch ist die Wahrscheinlichkeit, dass die zufällig gezogene Person eine Schuhgröße von weniger als 38 hat?

      pnorm(38, mean = 40, sd = 2)
      [1] 0.1586553

    3. Wie hoch ist die Wahrscheinlichkeit, dass die zufällig gezogene Person eine Schuhgröße zwischen 45 und 38 hat?

      pnorm(45, mean = 40, sd = 2) - pnorm(38, mean = 40, sd = 2)
      [1] 0.8351351

    4. Wie hoch ist die Wahrscheinlichkeit, dass die zufällig gezogene Person eine extreme Schuhgröße (mehr als 2 Standardabweichungen unter oder über dem Mittelwert) aufweist?

      1 - pnorm(44, mean = 40, sd = 2) + pnorm(36, mean = 40, sd = 2)
      [1] 0.04550026

      Oder

      2 * pnorm(36, mean = 40, sd = 2)
      [1] 0.04550026

      da die Normalverteilung symmetrisch ist.

      Statt beide Wahrscheinlichkeiten separat zu berechnen und zu addieren, kann diese Symmetrie ausgenutzt werden. Daher genügt es, die Wahrscheinlichkeit zu berechnen, dass eine Person extrem klein ist (also mehr als 2 Standardabweichungen unter dem Mittelwert liegt), und das Ergebnis einfach zu verdoppeln, um die Gesamtwahrscheinlichkeit für extreme Körpergrößen (über und unter dem Mittelwert) zu erhalten.

  1. Sie interessieren sich für die relative Häufigkeit von Suchterkrankungen in Deutschland. Sie ziehen zufällig und unabhängig voneinander n Person aus der Population, wobei jedoch alle Personen, die keine Schülerinnen sind, eine Wahrscheinlichkeit von Null haben, in die Stichprobe gezogen zu werden. Alle Schülerinnen haben die gleiche (positive) Wahrscheinlichkeit gezogen zu werden. Sie betrachten die Zufallsvariablen \(X_{1}\), \(X_{2}\), …, \(X_{i}\), …, \(X_{n}\), die jeweils den Wert 1 annehmen, falls die zufällig gezogene Person i unter einer Suchterkrankung leidet, und den Wert 0, falls nicht.

    1. Welcher Wahrscheinlichkeitsverteilung folgen die Zufallsvariablen \(X_{1}\), \(X_{2}\), …, \(X_{i}\), …, \(X_{n}\) jeweils?

      Die Stichprobe ist immer noch eine einfache Zufallsstichprobe, jedoch nur aus der Teilpopulation der Schülerinnen. Für die Zufallsvariablen gilt: \(X_{i}\ \sim\ Be(\pi)\) für alle i = 1, 2, …, n

    2. Welcher deskriptivstatistischen Maßzahl in welcher Population entspricht der Parameter dieser Verteilung?

      Der relativen Häufigkeit der Suchterkrankungen bei Schülerinnen.

    3. Welches Problem liegt hier bei der Stichprobenziehung vor?

      Fehlende Repräsentativität.

  1. Sie betrachten eine Population, die aus den Tieren Affe, Tiger, Giraffe, Elefant, Leopard, Kuh besteht. Sie ziehen eine einfache Zufallsstichprobe der Größe n = 2 aus dieser Population.

    1. Geben Sie zwei mögliche Ergebnisse dieses Zufallsexperiments an.

      Zum Beispiel:

      Giraffe, Kuh

      oder:

      Affe, Tiger

    2. Seien \(X_{1}\), \(X_{2}\) Zufallsvariablen, die jeweils den Wert 1 annehmen, falls der Name des ersten, zweiten, gezogenen Tieres auf e endet. Welcher Wahrscheinlichkeitsverteilung folgen die Zufallsvariablen?

      \(X_{i}\ \sim\ Be(\frac{1}{3})\) für alle i = 1, 2

    3. Welcher deskriptivstatistischen Maßzahl in der Population entspricht der Parameter dieser Verteilung?

      Der relativen Häufigkeit von Tieren, deren Namen auf e endet in der Population.

    4. Sie betrachten die Schätzfunktion \(\overline{X}\) für den Parameter der Wahrscheinlichkeitsverteilung von \(X_{1}\), \(X_{2}\). Geben Sie den Träger von \(\overline{X}\) an.

      \[T_{\overline{X}} = \left\{ 0, \frac{1}{2}, \ 1 \right\}\]

    5. Berechnen Sie den Erwartungswert von \(\overline{X}\). Interpretieren Sie diesen.

      \[E\left( \overline{X} \right) = \pi = \frac{1}{3}\]

      Falls man unendlich oft eine Stichprobe der Größe n = 2 aus der Population ziehen würde und jedes Mal den Schätzwert \(\overline{x}\) in der gezogenen Stichprobe berechnen würde, wäre der Mittelwert aller dieser Schätzwerte \(\frac{1}{3}\), würde also dem wahren Parameterwert \(\pi = \frac{1}{3}\) entsprechen.

    6. Berechnen Sie den Standardfehler von \(\overline{X}\). Interpretieren Sie diesen.

      \[SE\left( \overline{X} \right) = \sqrt{\frac{\pi(1 - \pi)}{n}} = \sqrt{\frac{1/3(1 - 1/3)}{2}} \approx 0.333\]

      Falls man unendlich oft eine Stichprobe der Größe n = 2 aus der Population ziehen würde und jedes Mal den Schätzwert \(\overline{x}\) in der gezogenen Stichprobe berechnen würde, wäre die empirische Standardabweichung aller dieser Schätzwerte 0.333.

  1. Gesucht ist der Anteil der Personen in Deutschland, bei denen im letzten Jahr eine Schlafstörung diagnostiziert wurde.

    1. Ihnen liegt eine einfache Zufallsstichprobe mit Umfang n = 560 vor. Nennen Sie eine geeignete Schätzfunktion für die relative Häufigkeit der Personen in Deutschland, bei denen im letzten Jahr eine Schlafstörung diagnostiziert wurde.

      Der Mittelwert von Bernoulli-Variablen entspricht der relativen Häufigkeit. Ein geeigneter Schätzer für die relative Häufigkeit für die Variable Schlafstörung in Deutschland wäre daher:

      \[\overline{X} = \frac{1}{n}\sum_{i = 1}^{n}X_{i}\]

    2. Geben Sie den Standardfehler dieser Schätzfunktion an.

      \[SE\left( \overline{X} \right) = \sqrt{\frac{\pi(1 - \pi)}{n}} = \sqrt{\frac{\pi(1 - \pi)}{560}}\]

    3. Bei 255 Personen in Ihrer Stichprobe wurde im letzten Jahr eine Schlafstörung diagnostiziert. Bestimmen Sie den Schätzwert und interpretieren Sie ihn.

      \[\overline{x} = h(1) = \frac{255}{560} \approx 0.455\]

      Auf Basis der Stichprobe wird der Anteil Deutscher, bei denen im letzten Jahr eine Schlafstörung diagnostiziert wurde, auf 45.5 % geschätzt.

  1. Sei X eine stetige Zufallsvariable, die für das Alter einer zufällig gezogenen Person steht. Gehen Sie davon aus, dass \(X\) normalverteilt ist mit \(\mu = 43\) und \(\sigma^{2} = 36\). Beantworten Sie die folgenden Fragen mit Hilfe der R-Funktion pnorm().

    1. Wie hoch ist die Wahrscheinlichkeit, dass die zufällig gezogene Person ein Alter von mehr als 48.3 hat?

      1 - pnorm(48.3, mean = 43, sd = 6)
      [1] 0.1885281

    2. Wie hoch ist die Wahrscheinlichkeit, dass die zufällig gezogene Person ein Alter von weniger als 41 hat?

      pnorm(41, mean = 43, sd = 6)
      [1] 0.3694413

    3. Wie hoch ist die Wahrscheinlichkeit, dass die zufällig gezogene Person ein Alter zwischen 48.3 und 41 hat?

      pnorm(48.3, mean = 43, sd = 6) - pnorm(41, mean = 43, sd = 6)
      [1] 0.4420306

    4. Wie hoch ist die Wahrscheinlichkeit, dass die zufällig gezogene Person ein extremes Alter (mehr als 2 Standardabweichungen unter oder über dem Mittelwert) aufweist?

      1 - pnorm(55, mean = 43, sd = 6) + pnorm(31, mean = 43, sd = 6)
      [1] 0.04550026

      Oder

      2 * pnorm(31, mean = 43, sd = 6)
      [1] 0.04550026

      da die Normalverteilung symmetrisch ist.

      Statt beide Wahrscheinlichkeiten separat zu berechnen und zu addieren, kann diese Symmetrie ausgenutzt werden. Daher genügt es, die Wahrscheinlichkeit zu berechnen, dass eine Person extrem klein ist (also mehr als 2 Standardabweichungen unter dem Mittelwert liegt), und das Ergebnis einfach zu verdoppeln, um die Gesamtwahrscheinlichkeit für extreme Körpergrößen (über und unter dem Mittelwert) zu erhalten.

  1. Sie interessieren sich für die relative Häufigkeit von Herzkrankheiten in Deutschland. Sie ziehen zufällig und unabhängig voneinander n Person aus der Population, wobei jedoch alle Personen, die keine Kardiologinnen sind, eine Wahrscheinlichkeit von Null haben, in die Stichprobe gezogen zu werden. Alle Kardiologinnen haben die gleiche (positive) Wahrscheinlichkeit gezogen zu werden. Sie betrachten die Zufallsvariablen \(X_{1}\), \(X_{2}\), …, \(X_{i}\), …, \(X_{n}\), die jeweils den Wert 1 annehmen, falls die zufällig gezogene Person i unter einer Herzkrankheit leidet, und den Wert 0, falls nicht.

    1. Welcher Wahrscheinlichkeitsverteilung folgen die Zufallsvariablen \(X_{1}\), \(X_{2}\), …, \(X_{i}\), …, \(X_{n}\) jeweils?

      Die Stichprobe ist immer noch eine einfache Zufallsstichprobe, jedoch nur aus der Teilpopulation der Kardiologinnen. Für die Zufallsvariablen gilt: \(X_{i}\ \sim\ Be(\pi)\) für alle i = 1, 2, …, n

    2. Welcher deskriptivstatistischen Maßzahl in welcher Population entspricht der Parameter dieser Verteilung?

      Der relativen Häufigkeit der Herzkrankheiten bei Kardiologinnen.

    3. Welches Problem liegt hier bei der Stichprobenziehung vor?

      Fehlende Repräsentativität.

  1. Sie betrachten eine Population, die aus den Superhelden Deadpool, Superman, Spiderman, Captain America, Batman, Iron Man besteht. Sie ziehen eine einfache Zufallsstichprobe der Größe n = 3 aus dieser Population.

    1. Geben Sie zwei mögliche Ergebnisse dieses Zufallsexperiments an.

      Zum Beispiel:

      Spiderman, Iron Man, Spiderman

      oder:

      Deadpool, Superman, Spiderman

    2. Seien \(X_{1}\), \(X_{2}\), \(X_{3}\) Zufallsvariablen, die jeweils den Wert 1 annehmen, falls der Name der ersten, zweiten, dritten gezogenen Superheld ‘man’ beinhaltet. Welcher Wahrscheinlichkeitsverteilung folgen die Zufallsvariablen?

      \(X_{i}\ \sim\ Be(\frac{2}{3})\) für alle i = 1, 2, 3

    3. Welcher deskriptivstatistischen Maßzahl in der Population entspricht der Parameter dieser Verteilung?

      Der relativen Häufigkeit von Superhelden, deren Namen ‘man’ beinhaltet in der Population.

    4. Sie betrachten die Schätzfunktion \(\overline{X}\) für den Parameter der Wahrscheinlichkeitsverteilung von \(X_{1}\), \(X_{2}\), \(X_{3}\). Geben Sie den Träger von \(\overline{X}\) an.

      \[T_{\overline{X}} = \left\{ 0, \frac{1}{3}, \frac{2}{3}, \ 1 \right\}\]

    5. Berechnen Sie den Erwartungswert von \(\overline{X}\). Interpretieren Sie diesen.

      \[E\left( \overline{X} \right) = \pi = \frac{2}{3}\]

      Falls man unendlich oft eine Stichprobe der Größe n = 3 aus der Population ziehen würde und jedes Mal den Schätzwert \(\overline{x}\) in der gezogenen Stichprobe berechnen würde, wäre der Mittelwert aller dieser Schätzwerte \(\frac{2}{3}\), würde also dem wahren Parameterwert \(\pi = \frac{2}{3}\) entsprechen.

    6. Berechnen Sie den Standardfehler von \(\overline{X}\). Interpretieren Sie diesen.

      \[SE\left( \overline{X} \right) = \sqrt{\frac{\pi(1 - \pi)}{n}} = \sqrt{\frac{2/3(1 - 2/3)}{3}} \approx 0.272\]

      Falls man unendlich oft eine Stichprobe der Größe n = 3 aus der Population ziehen würde und jedes Mal den Schätzwert \(\overline{x}\) in der gezogenen Stichprobe berechnen würde, wäre die empirische Standardabweichung aller dieser Schätzwerte 0.272.

  1. Gesucht ist der Anteil der Personen in Deutschland, bei denen im letzten Jahr eine Weitsichtigkeit diagnostiziert wurde.

    1. Ihnen liegt eine einfache Zufallsstichprobe mit Umfang n = 560 vor. Nennen Sie eine geeignete Schätzfunktion für die relative Häufigkeit der Personen in Deutschland, bei denen im letzten Jahr eine Weitsichtigkeit diagnostiziert wurde.

      Der Mittelwert von Bernoulli-Variablen entspricht der relativen Häufigkeit. Ein geeigneter Schätzer für die relative Häufigkeit für die Variable Weitsichtigkeit in Deutschland wäre daher:

      \[\overline{X} = \frac{1}{n}\sum_{i = 1}^{n}X_{i}\]

    2. Geben Sie den Standardfehler dieser Schätzfunktion an.

      \[SE\left( \overline{X} \right) = \sqrt{\frac{\pi(1 - \pi)}{n}} = \sqrt{\frac{\pi(1 - \pi)}{560}}\]

    3. Bei 255 Personen in Ihrer Stichprobe wurde im letzten Jahr eine Weitsichtigkeit diagnostiziert. Bestimmen Sie den Schätzwert und interpretieren Sie ihn.

      \[\overline{x} = h(1) = \frac{255}{560} \approx 0.455\]

      Auf Basis der Stichprobe wird der Anteil Deutscher, bei denen im letzten Jahr eine Weitsichtigkeit diagnostiziert wurde, auf 45.5 % geschätzt.

  1. Sei X eine stetige Zufallsvariable, die für das Gewicht einer zufällig gezogenen Person steht. Gehen Sie davon aus, dass \(X\) normalverteilt ist mit \(\mu = 75\) und \(\sigma^{2} = 4\). Beantworten Sie die folgenden Fragen mit Hilfe der R-Funktion pnorm().

    1. Wie hoch ist die Wahrscheinlichkeit, dass die zufällig gezogene Person ein Gewicht von mehr als 83.5 hat?

      1 - pnorm(83.5, mean = 75, sd = 2)
      [1] 1.068853e-05

    2. Wie hoch ist die Wahrscheinlichkeit, dass die zufällig gezogene Person ein Gewicht von weniger als 71 hat?

      pnorm(71, mean = 75, sd = 2)
      [1] 0.02275013

    3. Wie hoch ist die Wahrscheinlichkeit, dass die zufällig gezogene Person ein Gewicht zwischen 83.5 und 71 hat?

      pnorm(83.5, mean = 75, sd = 2) - pnorm(71, mean = 75, sd = 2)
      [1] 0.9772392

    4. Wie hoch ist die Wahrscheinlichkeit, dass die zufällig gezogene Person ein extremes Gewicht (mehr als 2 Standardabweichungen unter oder über dem Mittelwert) aufweist?

      1 - pnorm(79, mean = 75, sd = 2) + pnorm(71, mean = 75, sd = 2)
      [1] 0.04550026

      Oder

      2 * pnorm(71, mean = 75, sd = 2)
      [1] 0.04550026

      da die Normalverteilung symmetrisch ist.

      Statt beide Wahrscheinlichkeiten separat zu berechnen und zu addieren, kann diese Symmetrie ausgenutzt werden. Daher genügt es, die Wahrscheinlichkeit zu berechnen, dass eine Person extrem klein ist (also mehr als 2 Standardabweichungen unter dem Mittelwert liegt), und das Ergebnis einfach zu verdoppeln, um die Gesamtwahrscheinlichkeit für extreme Körpergrößen (über und unter dem Mittelwert) zu erhalten.

  1. Sie interessieren sich für die relative Häufigkeit von Mandelentzündungen in Deutschland. Sie ziehen zufällig und unabhängig voneinander n Person aus der Population, wobei jedoch alle Personen, die keine Kleinkinder sind, eine Wahrscheinlichkeit von Null haben, in die Stichprobe gezogen zu werden. Alle Kleinkinder haben die gleiche (positive) Wahrscheinlichkeit gezogen zu werden. Sie betrachten die Zufallsvariablen \(X_{1}\), \(X_{2}\), …, \(X_{i}\), …, \(X_{n}\), die jeweils den Wert 1 annehmen, falls die zufällig gezogene Person i unter einer Mandelentzündung leidet, und den Wert 0, falls nicht.

    1. Welcher Wahrscheinlichkeitsverteilung folgen die Zufallsvariablen \(X_{1}\), \(X_{2}\), …, \(X_{i}\), …, \(X_{n}\) jeweils?

      Die Stichprobe ist immer noch eine einfache Zufallsstichprobe, jedoch nur aus der Teilpopulation der Kleinkinder. Für die Zufallsvariablen gilt: \(X_{i}\ \sim\ Be(\pi)\) für alle i = 1, 2, …, n

    2. Welcher deskriptivstatistischen Maßzahl in welcher Population entspricht der Parameter dieser Verteilung?

      Der relativen Häufigkeit der Mandelentzündungen bei Kleinkinder.

    3. Welches Problem liegt hier bei der Stichprobenziehung vor?

      Fehlende Repräsentativität.

  1. Sie betrachten eine Population, die aus den Figuren Asterix, Obelix, Miraculix, Majestix, Troubadix, Caius Bonus besteht. Sie ziehen eine einfache Zufallsstichprobe der Größe n = 4 aus dieser Population.

    1. Geben Sie zwei mögliche Ergebnisse dieses Zufallsexperiments an.

      Zum Beispiel:

      Miraculix, Caius Bonus, Miraculix, Obelix

      oder:

      Asterix, Obelix, Miraculix, Troubadix

    2. Seien \(X_{1}\), \(X_{2}\), \(X_{3}\), \(X_{4}\) Zufallsvariablen, die jeweils den Wert 1 annehmen, falls der Name der ersten, zweiten, dritten, vierten gezogenen Figur auf x endet. Welcher Wahrscheinlichkeitsverteilung folgen die Zufallsvariablen?

      \(X_{i}\ \sim\ Be(\frac{5}{6})\) für alle i = 1, 2, 3, 4

    3. Welcher deskriptivstatistischen Maßzahl in der Population entspricht der Parameter dieser Verteilung?

      Der relativen Häufigkeit von Figuren, deren Namen auf x endet in der Population.

    4. Sie betrachten die Schätzfunktion \(\overline{X}\) für den Parameter der Wahrscheinlichkeitsverteilung von \(X_{1}\), \(X_{2}\), \(X_{3}\), \(X_{4}\). Geben Sie den Träger von \(\overline{X}\) an.

      \[T_{\overline{X}} = \left\{ 0, \frac{1}{4}, \frac{2}{4}, \frac{3}{4}, \ 1 \right\}\]

    5. Berechnen Sie den Erwartungswert von \(\overline{X}\). Interpretieren Sie diesen.

      \[E\left( \overline{X} \right) = \pi = \frac{5}{6}\]

      Falls man unendlich oft eine Stichprobe der Größe n = 4 aus der Population ziehen würde und jedes Mal den Schätzwert \(\overline{x}\) in der gezogenen Stichprobe berechnen würde, wäre der Mittelwert aller dieser Schätzwerte \(\frac{5}{6}\), würde also dem wahren Parameterwert \(\pi = \frac{5}{6}\) entsprechen.

    6. Berechnen Sie den Standardfehler von \(\overline{X}\). Interpretieren Sie diesen.

      \[SE\left( \overline{X} \right) = \sqrt{\frac{\pi(1 - \pi)}{n}} = \sqrt{\frac{5/6(1 - 5/6)}{4}} \approx 0.186\]

      Falls man unendlich oft eine Stichprobe der Größe n = 4 aus der Population ziehen würde und jedes Mal den Schätzwert \(\overline{x}\) in der gezogenen Stichprobe berechnen würde, wäre die empirische Standardabweichung aller dieser Schätzwerte 0.186.

  1. Gesucht ist der Anteil der Personen in Deutschland, bei denen im letzten Jahr eine Zwangsstörung diagnostiziert wurde.

    1. Ihnen liegt eine einfache Zufallsstichprobe mit Umfang n = 515 vor. Nennen Sie eine geeignete Schätzfunktion für die relative Häufigkeit der Personen in Deutschland, bei denen im letzten Jahr eine Zwangsstörung diagnostiziert wurde.

      Der Mittelwert von Bernoulli-Variablen entspricht der relativen Häufigkeit. Ein geeigneter Schätzer für die relative Häufigkeit für die Variable Zwangsstörung in Deutschland wäre daher:

      \[\overline{X} = \frac{1}{n}\sum_{i = 1}^{n}X_{i}\]

    2. Geben Sie den Standardfehler dieser Schätzfunktion an.

      \[SE\left( \overline{X} \right) = \sqrt{\frac{\pi(1 - \pi)}{n}} = \sqrt{\frac{\pi(1 - \pi)}{515}}\]

    3. Bei 113 Personen in Ihrer Stichprobe wurde im letzten Jahr eine Zwangsstörung diagnostiziert. Bestimmen Sie den Schätzwert und interpretieren Sie ihn.

      \[\overline{x} = h(1) = \frac{113}{515} \approx 0.219\]

      Auf Basis der Stichprobe wird der Anteil Deutscher, bei denen im letzten Jahr eine Zwangsstörung diagnostiziert wurde, auf 21.9 % geschätzt.

Fußnoten

  1. x-Achse von -3 bis 3, y-Achse von 0.0 bis 0.4, Dichtefunktion der Normalverteilung eingezeichnet mit Maximum bei x = 0 und y = 0.4

    Dichtefunktion der Standardnormalverteilung
    ↩︎