Bonusseminar 5: Standardfehler und Konfidenzniveau simulieren

Warum soll ich lernen wie man Daten simuliert?

  • Tieferes Verständnis von statistischen Verfahren: Simulation statt Beweis (weniger mathematische Kenntnisse notwendig)
  • Überprüfen von statistischen Eigenschaften für nahezu beliebige Szenarien
  • Validierung von Auswertungsstrategien: Funktioniert eine geplante Analysen mit simulierten Daten und zeigt dort die gewünschten Eigenschaften?
  • Nützliche Programmierskills, die auch in anderen Kontexten helfen

Nützliche R Funktionen für Simulationen

HinweisWiederholung

rnorm and friends

x <- rnorm(n = 1000, mean = 0, sd = 1)
head(x)
[1] -1.09608717  0.16152924 -0.71526323 -0.88594076  0.62002611  0.01948096
hist(x)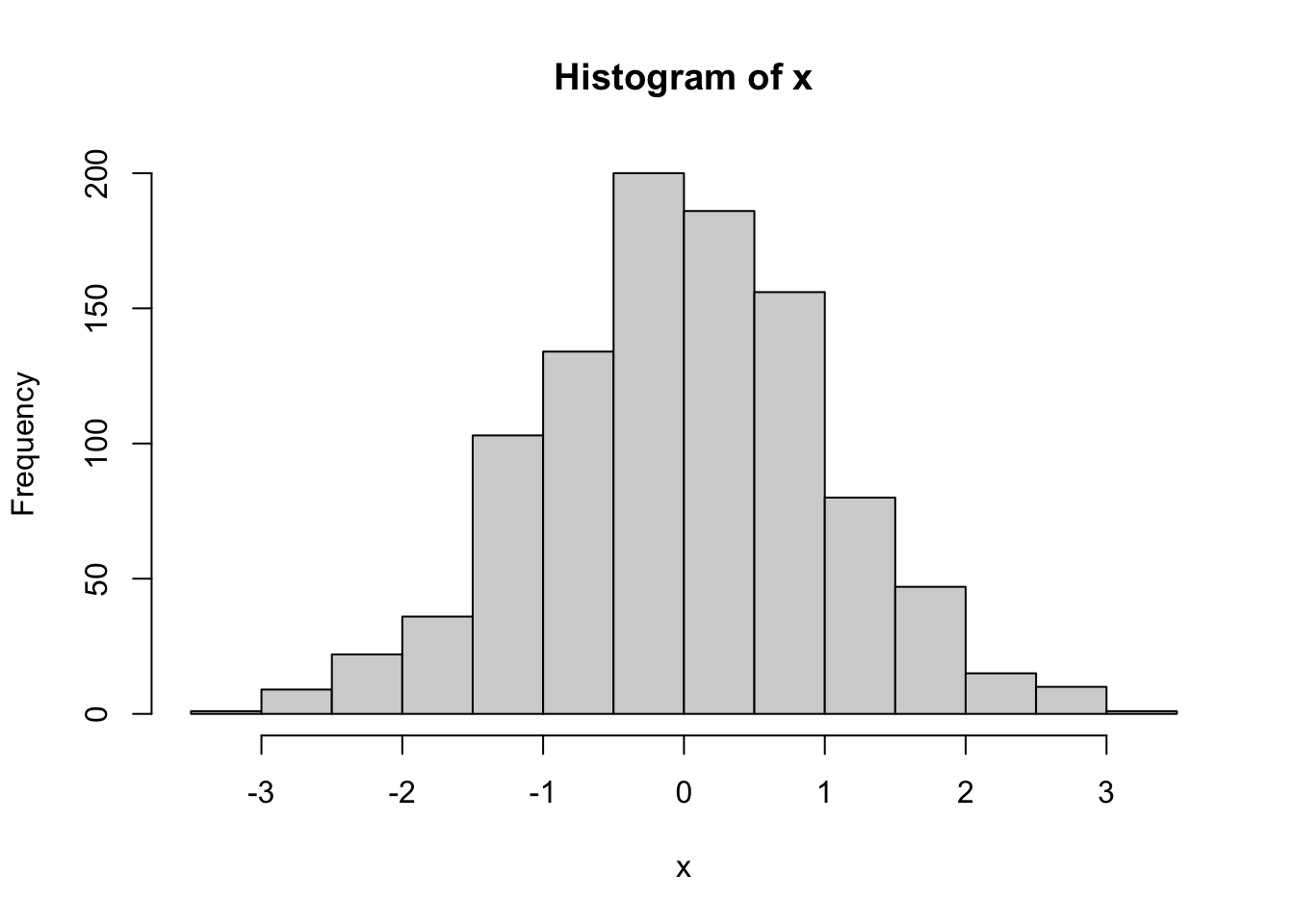

set.seed

set.seed(1)
rnorm(1)
[1] -0.6264538
rnorm(1)
[1] 0.1836433
set.seed(1)
rnorm(1)
[1] -0.6264538
rnorm(1)
[1] 0.1836433

Eigene Funktionen erstellen

my_mean <- function(Vektor){
  sum(Vektor) / length(Vektor)
}
my_mean(x)
[1] -0.01264102

Listen

my_list <- list(number = 1256, name = "Tomas", vector = c(1, 2, 5, 6))
my_list
$number
[1] 1256

$name
[1] "Tomas"

$vector
[1] 1 2 5 6
my_list$vector
[1] 1 2 5 6
my_list[["vector"]] # alternativ
[1] 1 2 5 6
my_list[[3]][[2]] # einzelne Elemente herausgreifen
[1] 2

replicate

Mit replicate(R, BEFEHL, simplify = FALSE) können wir einen Befehl sehr einfach R mal wiederholen. Wir könnten stattdessen auch einen for-Loop verwenden, aber zumindest für einfache Beispiele ist replicate oft praktischer.

R <- 5
n <- 3
set.seed(1)
x_list <- replicate(R, rnorm(n = n, mean = 170, sd = sqrt(100)), simplify = FALSE)
str(x_list)
List of 5
 $ : num [1:3] 164 172 162
 $ : num [1:3] 186 173 162
 $ : num [1:3] 175 177 176
 $ : num [1:3] 167 185 174
 $ : num [1:3] 164 148 181

lapply

Mit lapply(LISTE, FUN = FUNKTION) können wir eine FUNKTION auf jedes Element von LISTE anwenden. Das Ergebnis von lapply ist wieder eine Liste mit der gleichen Länge wie LISTE. Die Elemente der Liste sind die Ergebnisse von FUNKTION, angewendet auf die entsprechenden Elemente in LISTE. Wenn wir die Liste in einen Vektor überführen wollen, können wir die Funktion unlist() verwenden.

sums <- lapply(x_list, FUN = sum)
sums
[[1]]
[1] 497.2156

[[2]]
[1] 521.0432

[[3]]
[1] 528.0154

[[4]]
[1] 525.9624

[[5]]
[1] 492.8899
unlist(sums)
[1] 497.2156 521.0432 528.0154 525.9624 492.8899

ÜBUNG: Simulation Standardfehler

  1. Nehmen Sie an, das Merkmal Intelligenz ist in der Population normalverteilt mit den Parametern \(\mu = 100\) und \(\sigma = 15\).

    • Simulieren Sie R = 100000 Stichproben der Größe n = 100.
    • Schätzen Sie für jede Stichprobe den Parameter \(\mu\).
    • Betrachten Sie die Verteilung der Schätzwerte grafisch.
    • Berechnen Sie den Mittelwert der Schätzwerte und vergleichen Sie diesen mit dem Mittelwert des Merkmals in der Population.
    • Berechnen Sie die Varianz der Schätzwerte und vergleichen Sie diese mit der Varianz des Merkmals in der Population.
    • Berechnen Sie die Standardabweichung der Schätzwerte und vergleichen Sie diese mit dem Ergebnis der Formel für den Standardfehler der Schätzfunktion.
    • Berechnen Sie die relative Häufigkeit der Stichproben, in denen der Schätzwert weniger als 1 IQ Punkt von \(\mu\) abweicht. Vergleichen Sie das Ergebnis mit der Wahrscheinlichkeit für dieses Ereignis (Berechnung mithilfe von pnorm() unter Berücksichtigung der Verteilung der Schätzfunktion).
# Ziehe R Stichproben der Größe n
R <- 100000
n <- 100
set.seed(1)
x_list <- replicate(R, rnorm(n = n, mean = 100, sd = sqrt(225)), simplify = FALSE)
str(x_list)
List of 100000
 $ : num [1:100] 90.6 102.8 87.5 123.9 104.9 ...
 $ : num [1:100] 90.7 100.6 86.3 102.4 90.2 ...
 $ : num [1:100] 106.1 125.3 123.8 95 65.7 ...
 $ : num [1:100] 113.4 84.3 129.6 94.2 124.8 ...
 $ : num [1:100] 116.1 128.4 91 94.1 93.8 ...
 $ : num [1:100] 101.2 95.5 82.3 100.2 114.9 ...
 $ : num [1:100] 94.9 122.5 107.9 108.1 97.9 ...
 $ : num [1:100] 89.4 129.6 98.7 99.8 83.1 ...
 $ : num [1:100] 83.7 72.6 114.9 99.8 91 ...
 $ : num [1:100] 76.9 102.9 104 83.2 109.8 ...
 $ : num [1:100] 117 116.7 86.9 103.2 101 ...
 $ : num [1:100] 103.6 83 122.3 96.3 102.8 ...
 $ : num [1:100] 76.6 128.8 72.1 68.4 110.5 ...
 $ : num [1:100] 105.1 119.7 85.6 81.9 123.5 ...
 $ : num [1:100] 123.2 102.7 95.8 88.5 91.4 ...
 $ : num [1:100] 112.8 86.1 113.4 85.9 108.1 ...
 $ : num [1:100] 105.2 100.2 86.9 105.1 97.3 ...
 $ : num [1:100] 124.3 95.1 65.1 132.9 83.8 ...
 $ : num [1:100] 110.7 108.7 97.8 122.6 95.8 ...
 $ : num [1:100] 91.4 104.3 117.2 102.1 101.3 ...
 $ : num [1:100] 86.7 71.2 124.3 107.8 99.2 ...
 $ : num [1:100] 79.9 99.3 132.8 121.3 102.7 ...
 $ : num [1:100] 113.8 112.1 89.3 59.7 91.5 ...
 $ : num [1:100] 95.3 103.1 90.2 82.7 107.9 ...
 $ : num [1:100] 94.4 114.9 101.5 122.2 108.4 ...
 $ : num [1:100] 72.9 89.8 92.9 115.4 91 ...
 $ : num [1:100] 114 112 101 100 123 ...
 $ : num [1:100] 93.9 129.1 107.3 97 82.5 ...
 $ : num [1:100] 68.4 98.7 111.3 76.3 110.6 ...
 $ : num [1:100] 111.7 99.3 101.4 80 108.2 ...
 $ : num [1:100] 111.1 105.8 119.4 87.9 76 ...
 $ : num [1:100] 104.7 102.5 114.4 98 99.3 ...
 $ : num [1:100] 98.3 112.8 97.2 121.4 131.2 ...
 $ : num [1:100] 93.3 89.9 106.2 91.2 80.9 ...
 $ : num [1:100] 84.3 93.6 96.5 117.9 108.1 ...
 $ : num [1:100] 107.8 105.7 90.6 91.4 104.7 ...
 $ : num [1:100] 125.9 87.8 74.6 122.4 110.6 ...
 $ : num [1:100] 113 77.7 94 90.4 103.2 ...
 $ : num [1:100] 89.1 96.3 90.8 101.6 88 ...
 $ : num [1:100] 104 102 112 113 105 ...
 $ : num [1:100] 83 111.5 108.6 79.7 69.6 ...
 $ : num [1:100] 106.1 106.4 83.5 95 103.5 ...
 $ : num [1:100] 77.8 115.4 66.7 75.4 105.4 ...
 $ : num [1:100] 93.9 115 85.5 111.4 101.2 ...
 $ : num [1:100] 87.4 106.7 94.5 108.1 87.9 ...
 $ : num [1:100] 123.4 89.1 77.4 91.5 68.4 ...
 $ : num [1:100] 90.6 78.6 101.9 91.4 101.5 ...
 $ : num [1:100] 99.3 108.5 110.4 118.6 99 ...
 $ : num [1:100] 82.9 117.6 92.9 124.7 95.1 ...
 $ : num [1:100] 68.2 90.1 104.8 98.5 99.4 ...
 $ : num [1:100] 77.3 109.4 74.8 117.7 116.8 ...
 $ : num [1:100] 113.2 120.7 120.1 88.7 95.5 ...
 $ : num [1:100] 106.9 124.7 119.7 102.6 89.5 ...
 $ : num [1:100] 78.3 110.2 100.7 101.2 98.2 ...
 $ : num [1:100] 105.2 114.3 66.6 88.4 98.9 ...
 $ : num [1:100] 82.9 85.7 124.3 102.5 86.4 ...
 $ : num [1:100] 110.4 97.1 106.4 108.4 87.3 ...
 $ : num [1:100] 95 88.7 100.4 96.8 87.9 ...
 $ : num [1:100] 98 95.4 107.2 104.3 93.4 ...
 $ : num [1:100] 99.8 113.5 87.1 51.5 97.8 ...
 $ : num [1:100] 90.7 83.4 67.4 99.5 96.1 ...
 $ : num [1:100] 117.5 130.3 96 98.8 96.1 ...
 $ : num [1:100] 81.6 102.2 92.1 105.1 101.6 ...
 $ : num [1:100] 100.9 108.5 108 85.9 107 ...
 $ : num [1:100] 106.5 97 113.9 79.5 77.4 ...
 $ : num [1:100] 113.3 94.3 101.7 74.1 111.2 ...
 $ : num [1:100] 95.6 114.2 85.5 80.7 119.7 ...
 $ : num [1:100] 113 103.8 89.3 108.8 124.7 ...
 $ : num [1:100] 102.3 109 86.1 95.4 88.5 ...
 $ : num [1:100] 112 103 119 109 104 ...
 $ : num [1:100] 80.1 114.3 112.9 115.9 94.7 ...
 $ : num [1:100] 96.9 69.8 84.5 97 103.1 ...
 $ : num [1:100] 101.1 106.8 97.6 112.7 99.6 ...
 $ : num [1:100] 118.5 125.5 93.3 93.6 105.1 ...
 $ : num [1:100] 110.4 78.2 101.9 75.8 112.9 ...
 $ : num [1:100] 88.1 109.1 84.1 115.3 102.7 ...
 $ : num [1:100] 117.9 99.5 112.1 87 100.2 ...
 $ : num [1:100] 86.4 87.1 122.9 95.1 90.2 ...
 $ : num [1:100] 108.4 94.4 89 100.8 90.6 ...
 $ : num [1:100] 81.6 105.4 120.5 123.4 80.3 ...
 $ : num [1:100] 104 87.6 78.1 125.3 76.8 ...
 $ : num [1:100] 92.9 97.8 107.7 109.6 100.3 ...
 $ : num [1:100] 104 85 151 106 135 ...
 $ : num [1:100] 91.1 66.3 108.1 75.8 100.2 ...
 $ : num [1:100] 125.1 96.5 99.8 104.3 96.6 ...
 $ : num [1:100] 114.9 99 103.9 90.7 88.4 ...
 $ : num [1:100] 79.8 107.8 115.1 111.4 107.2 ...
 $ : num [1:100] 102 105 104 108 124 ...
 $ : num [1:100] 114.5 77.1 118.3 95.2 108.5 ...
 $ : num [1:100] 83.2 101.8 96.2 86 87.8 ...
 $ : num [1:100] 81.7 85.8 101.4 110.5 110.1 ...
 $ : num [1:100] 117.3 119.7 76.5 101.3 99.4 ...
 $ : num [1:100] 89.1 99.2 144.4 94.2 89.2 ...
 $ : num [1:100] 91.2 107.4 90.9 94.6 93 ...
 $ : num [1:100] 116.6 103.1 88.4 98.7 81.1 ...
 $ : num [1:100] 119.5 78.6 103.6 96.8 101.2 ...
 $ : num [1:100] 116.5 86.5 82.9 111.5 83.9 ...
 $ : num [1:100] 110.9 83.8 96 92.5 77 ...
 $ : num [1:100] 84.9 82.2 82.2 116.1 85.6 ...
  [list output truncated]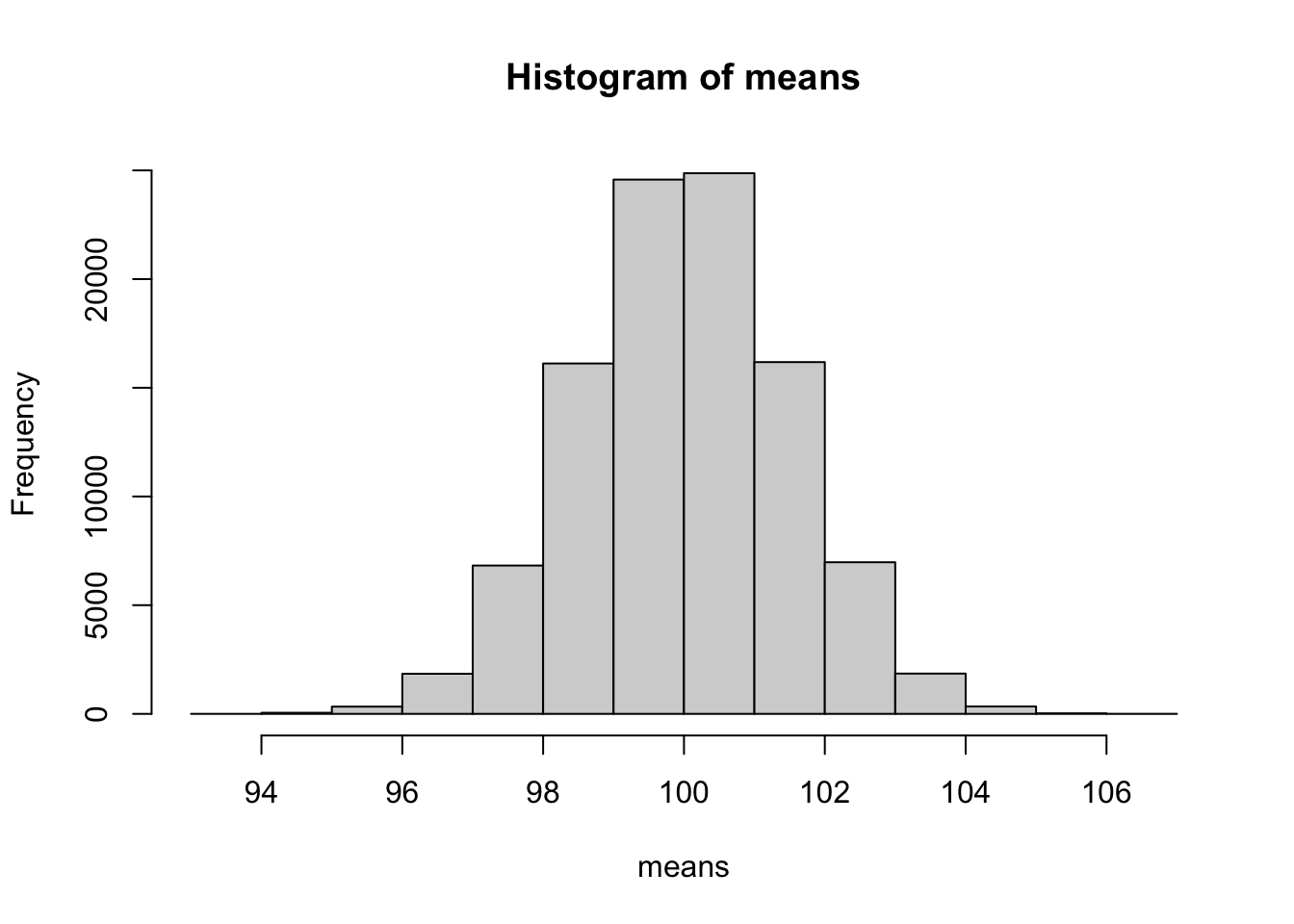
# Berechne für jede Stichprobe den Schätzwert (also den Mittelwert)
means_list <- lapply(x_list, mean)
means <- unlist(means_list)
# Plotte die Verteilung der Schätzwerte
hist(means)

# Berechne den Mittelwert der Schätzwerte
mean(means)
[1] 100.0061
# Berechne die Varianz der Schätzwerte
var(means)
[1] 2.244553
# Berechne die Standardabweichung der Schätzwerte
sd(means)
[1] 1.498183
# Berechne den wahren Standardfehler per Formel
sqrt(225/n)
[1] 1.5
# Berechne die relative Häufigkeit von 99 < Schätzwert < 101
sum(means > 99 & means < 101)/R
[1] 0.49448
# Berechne die wahre Wahrscheinlichkeit
pnorm(101, mean = 100, sd = sqrt(225/n)) - pnorm(99, mean = 100, sd = sqrt(225/n))
[1] 0.4950149

Fazit:

  • Die Simulation approximiert die tatsächliche Verteilung der Schätzfunktion: \(\bar{X} \sim N(\mu, \frac{\sigma^2}{N})\)
  • Mithilfe der Realisationen \(\bar{x}\) aus der Simulation können Wahrscheinlichkeiten bzgl. \(\bar{X}\) durch relative Häufigkeiten approximiert werden.

ÜBUNG: Simulation Konfidenzniveau

  1. Nehmen Sie erneut an, das Merkmal Intelligenz ist in der Population normalverteilt mit den Parametern \(\mu = 100\) und \(\sigma = 15\).

    • Sie können die simulierten Stichproben aus der letzten Übungsaufgabe übernehmen.
    • Schätzen Sie für jede Stichprobe den Parameter \(\mu\) mithilfe eines 95%-Konfidenzintervalls.
    • Berechnen Sie die relative Häufigkeit der Stichproben, in denen das Konfidenzintervall den Parameter \(\mu\) enthält und vergleichen Sie diese mit dem theoretischen Konfidenzniveau.
# Berechne für jede Stichprobe ein KI
ki <- function(x){
  t.test(x, conf.level = 0.95)$conf.int
}
kis <- lapply(x_list, ki)
str(kis)
List of 100000
 $ : num [1:2] 99 104
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 96.6 102.3
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 97.4 103.5
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 97.8 103.7
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 95.9 102.9
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 96.5 102.2
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 93.8 100.2
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 96.7 103.3
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 96.9 103.4
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 96.9 103.2
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 96.8 102.9
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 94.8 100.7
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 100 107
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 94.8 100
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 98.1 104.3
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 96.6 102.9
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 95.6 101.5
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 95.2 102.2
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 98.9 105.2
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 95.7 102
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 94.7 101
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 97.6 104.1
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 96.5 102.4
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 98.9 104.7
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 97.6 103.9
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 94.7 99.9
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 98.3 104
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 98 104
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 97.7 104.2
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 97.8 104.4
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 98.7 105.6
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 98.7 104.9
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 98.8 105.1
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 98.1 104.4
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 96.6 102.6
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 97.4 103.3
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 95.2 101.6
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 94.5 100.7
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 96.7 103.1
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 96.9 102
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 96.9 102.7
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 96.3 102.1
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 96 103
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 98.2 103.8
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 97.4 102.9
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 94.5 100.6
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 100 105
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 96.4 102.7
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 96.4 102
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 95.4 101.5
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 95.4 101.3
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 98.3 103.7
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 97.4 102.9
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 97.1 102.7
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 96.7 102.5
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 95 101
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 98 104
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 98.4 104.1
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 94.7 100.6
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 98.2 104
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 96.2 102.1
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 97.7 104.6
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 94.8 101.4
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 97.5 103.7
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 97.9 104.2
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 94.6 100.4
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 99.8 105.5
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 98 104
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 94.3 100.8
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 95.3 101
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 96.3 102.4
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 97 102
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 94.5 100.1
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 99.6 105.8
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 97.3 103.7
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 97.8 103.9
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 96.7 102.6
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 96.4 102.3
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 97.7 103.7
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 96.3 102.3
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 97.1 102.4
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 96.6 102.4
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 97.5 104.6
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 94.9 101.3
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 94 100
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 96.7 102.4
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 94.9 100.7
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 98 103
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 97.4 102.9
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 100 106
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 97.4 102.8
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 97.4 103
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 98.2 104.3
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 95.9 101.4
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 98.4 104.8
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 97.3 103.1
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 96.5 102.8
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 97.5 103.6
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 96.2 102
  ..- attr(*, "conf.level")= num 0.95
  [list output truncated]
# Überprüfe für jedes KI, ob das wahre mu enthalten ist
hit <- function(ki, mu = 100){
  mu > ki[1] & mu < ki[2] 
}
hits <- unlist(lapply(kis, hit))
str(hits)
 logi [1:100000] TRUE TRUE TRUE TRUE TRUE TRUE ...
# Schätze das Konfidenzniveau
sum(hits)/length(hits)
[1] 0.95106
mean(hits) # oder äquivalent mit TRUE == 1 und FALSE == 0 Trick
[1] 0.95106

Fazit:

  • In der Simulation wird eins zu eins die Definition des Konfidenzniveaus nachgebaut: Bei Ziehung unendlich vieler einfacher Zufallsstichproben (in der Simulation nicht unendlich viele, aber sehr viele) enthalten 95% der Konfidenzintervalle den wahren Parameterwert.

ÜBUNG: Standardfehler und Konfidenzniveau bei Verletzung der Verteilungsannahme

Angenommen, die Intelligenz ist eigentlich in der Population gumbelverteilt mit Location-Parameter \(\mu = 100\) und Scale-Parameter \(\beta = 15\). Auf den ersten Blick sieht die Gumbelverteilung mit diesen Parametern vielleicht ein bisschen ähnlich aus als die Normalverteilung mit \(\mu = 100\) und \(\sigma = 15\), jedoch ist die Gumbelverteilung nicht symmetrisch:

library(ordinal)
curve(dgumbel(x, location = 100, scale = 15), from = 70, to = 160, 
  xlab = "x", ylab = "f(x)")

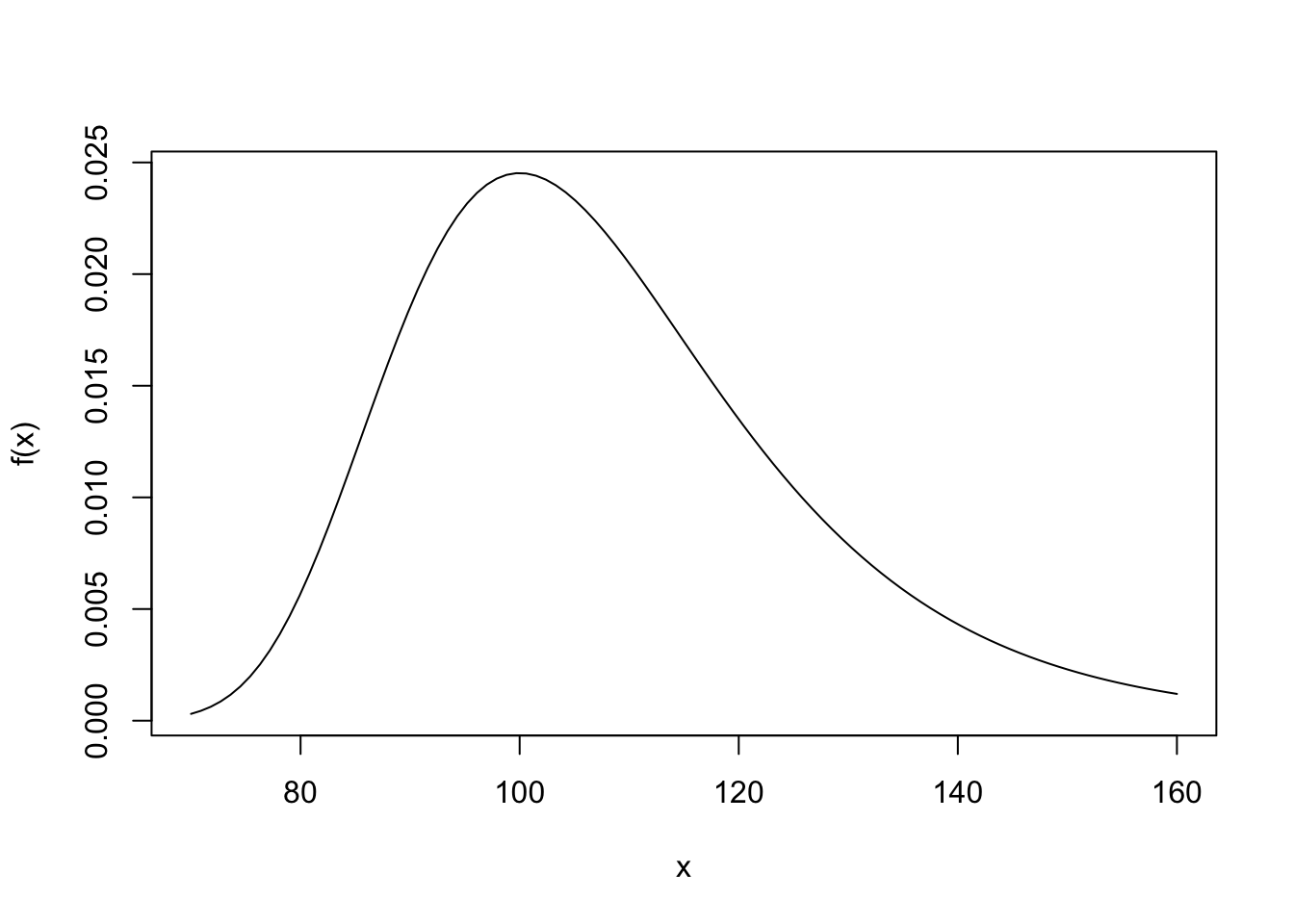
  1. Überlegen Sie sich mithilfe einer Datensimulation, was passiert wenn das Merkmal eigentlich gumbelverteilt ist, Sie aber bei der Parameterschätzung annehmen, das Merkmal wäre normalverteilt.

    • Verwenden Sie \(\bar{X}\) als Schätzfunktion für den Location-Parameter der Gumbelverteilung.
    • Überprüfen Sie mithilfe einer Simulation, ob die Schätzfunktion erwartungstreu ist.
    • Schätzen Sie den Standardfehler von \(\bar{X}\) mithilfe einer Simulation.
    • Verwenden Sie das normale 95%-Konfidenzintervall für normalverteilte Merkmale, um den Location-Parameter der Gumbelverteilung zu schätzen.
    • Überprüfen Sie das Konfidenzniveau mithilfe einer Simulation.
    • Überprüfen Sie, wie häufig in den Konfidenzintervallen der Erwartungswert des Merkmals in der Population enthalten ist. Für den Erwartungswert einer gumbelverteilten Zufallsvariable \(X\) gilt: \(E(X) \approx \mu + \beta \cdot 0.5772\)
# Paket laden um aus der Gumbelverteilung simulieren zu können (rgumbel)
library(ordinal)
# Ziehe R Stichproben der Größe n
R <- 100000
n <- 100
set.seed(1)
x_list <- replicate(R, rgumbel(n = n, location = 100, scale = 15), simplify = FALSE)
# Berechne für jede Stichprobe den Schätzwert (also den Mittelwert)
means_list <- lapply(x_list, mean)
means <- unlist(means_list)
# Plotte die Verteilung der Schätzwerte
hist(means)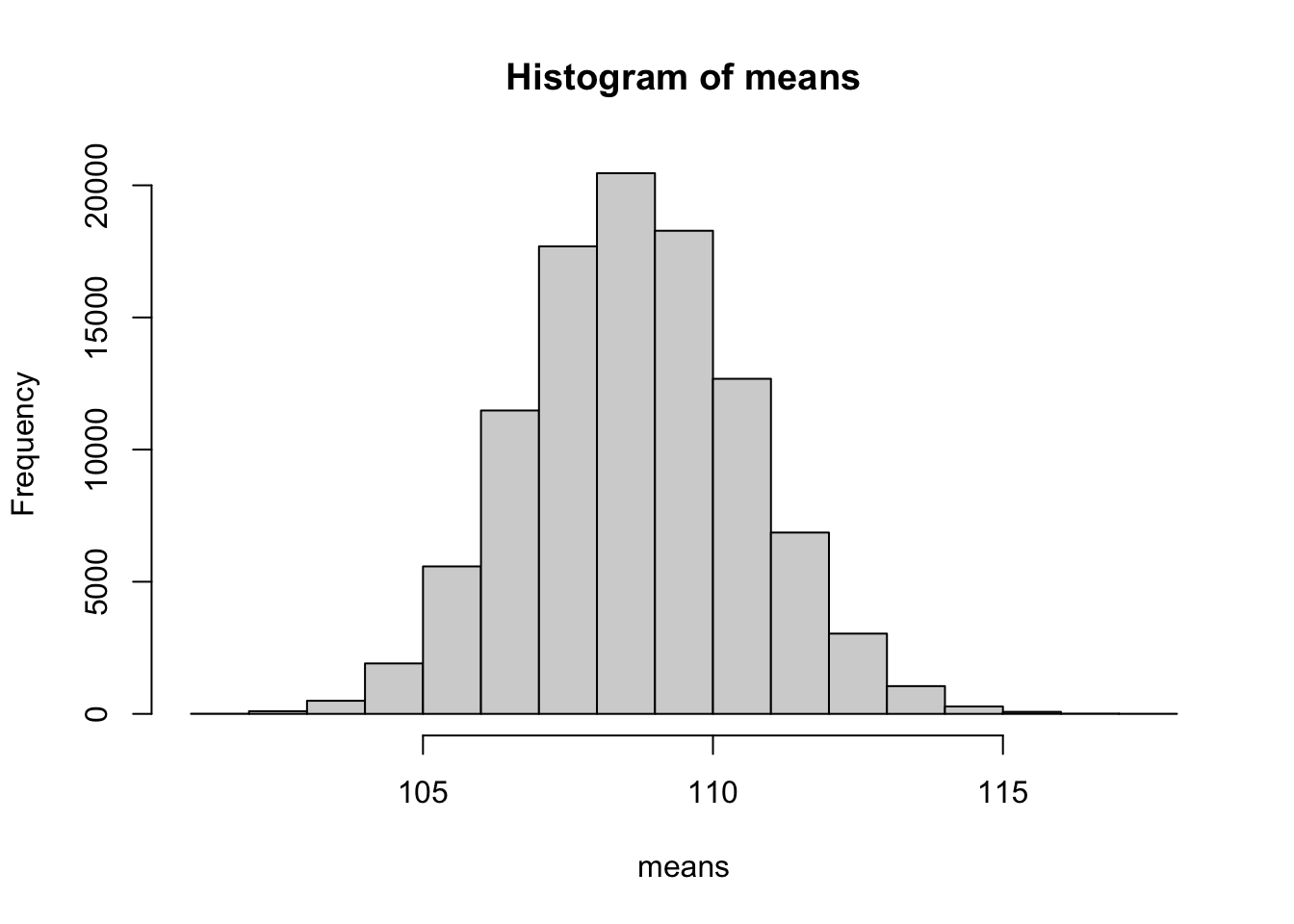

# Berechne den Mittelwert der Schätzwerte
mean(means)
[1] 108.6571
# Berechne die Standardabweichung der Schätzwerte
sd(means)
[1] 1.924966
# Berechne für jede Stichprobe ein KI
ki <- function(x){
  t.test(x, conf.level = 0.95)$conf.int
}
kis <- lapply(x_list, ki)
str(kis)
List of 100000
 $ : num [1:2] 106 112
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 106 113
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 102 109
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 106 114
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 105 113
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 107 114
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 106 113
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 104 113
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 104 112
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 105 114
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 104 112
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 103 110
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 104 112
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 103 110
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 104 111
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 106 114
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 106 115
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 103 111
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 106 114
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 103 112
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 103 110
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 104 112
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 103 110
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 105 112
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 106 114
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 109 118
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 102 108
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 103 109
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 106 114
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 104 112
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 105 112
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 104 112
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 106 114
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 103 111
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 108 117
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 103 110
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 109 118
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 104 112
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 102 111
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 104 111
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 105 113
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 103 111
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 104 113
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 106 115
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 104 111
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 105 114
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 107 114
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 107 114
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 106 114
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 105 112
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 103 110
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 106 113
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 106 112
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 106 113
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 108 116
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 108 116
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 106 114
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 107 114
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 104 111
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 105 112
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 106 114
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 106 115
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 107 115
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 106 113
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 107 114
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 104 112
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 106 114
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 104 111
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 108 114
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 105 113
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 106 113
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 103 111
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 103 111
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 108 117
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 103 111
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 103 110
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 107 115
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 103 111
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 103 110
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 104 110
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 105 113
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 102 109
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 105 112
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 103 110
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 106 115
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 104 113
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 107 114
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 106 113
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 104 111
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 105 112
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 104 112
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 106 113
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 106 113
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 107 114
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 107 116
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 102 109
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 105 112
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 104 110
  ..- attr(*, "conf.level")= num 0.95
 $ : num [1:2] 104 112
  ..- attr(*, "conf.level")= num 0.95
  [list output truncated]
# Überprüfe für jedes KI, ob das wahre mu der Gumbelverteilung enthalten ist
hit <- function(ki, mu = 100){
  mu > ki[1] & mu < ki[2] 
}
hits <- unlist(lapply(kis, hit))
# Schätze Konfidenzniveau für den Parameter der Gumbelverteilung
mean(hits)
[1] 0.00183
# Überprüfe für jedes KI, ob der Erwartungswerts enthalten ist
hit_E <- function(ki, mu = 100 + 15 * 0.5772){
  mu > ki[1] & mu < ki[2] 
}
hits_E <- unlist(lapply(kis, hit_E))
# Schätze das Konfidenzniveau für den Erwartungswert des Merkmals
mean(hits_E)
[1] 0.94739

Fazit:

  • Die Schätzfunktion \(\bar{X}\) ist nicht erwartungstreu für den Location-Parameter \(\mu\) einer Gumbelverteilung. Wir sehen dass der Mittelwert der Schätzwerte relativ weit vom wahren Wert \(\mu = 100\) entfernt liegt.
  • Auch wenn \(\bar{X}\) hier also keine gute Schätzfunktion für den Location-Parameter ist, können wir mithilfe der Simulation den Standardfehler (also die Standardabweichung) der Schätzfunktion beliebig genau approximieren, ohne dass wir die Formel für die Berechnung des Standardfehlers für diesen Fall kennen.
  • Wie man direkt auf den ersten Blick sehen kann, entspricht das wahre Konfidenzniveau für unser normales 95%-Konfidenzintervall nicht mehr 0.95, sondern liegt sehr nahe an 0. Weil die für das hier berechnete KI notwendige Verteilungsannahme verletzt ist (das Merkmal ist in der Population nicht normalverteilt), hält das Konfidenzintervall sein Konfidenzniveau nicht ein.
  • Das von uns besprochene “normale” Konfidenzintervall hat jedoch sehr praktische approximative Eigenschaften: Solange die Stichprobe groß genug ist, können wir das Konfidenzintervall für die Schätzung des Erwartungswerts (also dem Mittelwert des Merkmals in der Population) verwenden und das von uns eingestellte Konfidenzniveau gilt approximativ immer noch. Dafür muss das Merkmal in der Population nicht normalverteilt sein. Mithilfe unserer Simulation könnten wir auch versuchen herausfinden, was “solange die Stichprobe groß genug ist” in unserem Beispiel bedeutet. Wenn die wahre Verteilung der Normalverteilung sehr unähnlich ist, kann es sein, dass die Stichprobe sehr groß sein muss, damit das Konfidenzintervall einigermaßen funktioniert. Bei unserer Gumbelverteilung scheint es aber schon mit einer Stichprobengröße von \(N = 100\) ganz gut zu funktionieren.