qt(0.0025, 4)[1] -5.597568Einführung in statistische Hypothesentests
Geben Sie für die folgenden Hypothesen jeweils an, ob es sich um inhaltliche oder statistische Hypothesen handelt:
\(\pi = 0.75\)
Statistische Hypothese
\(\mu > 0.75\)
Statistische Hypothese
\(s_{emp}^{2} \neq 100\)
Inhaltliche Hypothese
\({\overline{x}}_{Männer} - {\overline{x}}_{Frauen} < 0\)
Inhaltliche Hypothese
\(h_{Depression} - h_{Angst} = 0\ \)
Inhaltliche Hypothese
Geben Sie für die folgenden Hypothesen jeweils an, ob es sich um gerichtete (links- oder rechtsgerichtet) oder ungerichtete Hypothesen handelt:
\({\overline{x}}_{Frauen} \neq 100\)
Ungerichtete Hypothese
\({\overline{x}}_{Frauen}\ < 0.5\)
(Links-)Gerichtete Hypothese
\(\pi \geq 0.3\)
(Rechts-)Gerichtete Hypothese
\(\mu_{1} = \mu_{2}\)
Ungerichtete Hypothese
Nennen und erläutern Sie die beiden Gütekriterien statististischer Hypothesentests. Wie können Sie jeweils sicherstellen, dass diese gegeben sind?
Geringes Signifikanzniveau:
Ein geringes Signifikanzniveau bedeutet, dass die Wahrscheinlichkeit für einen Fehler erster Art gering ist. Dies kann durch die Wahl eines geeigneten kritischen Bereichs sichergestellt werden.
Hohe Power:
Eine hohe Power bedeutet, dass die Wahrscheinlichkeit für einen Fehler zweiter Art gering ist. Dies kann durch einen großen Stichprobenumfang sichergestellt werden.
Sind die folgenden Aussagen im Kontext statistischer Hypothesentests jeweils wahr oder falsch? Begründen Sie.
\(\alpha + \beta = 1\)
Falsch. \(\alpha\) ist die Wahrscheinlichkeit für einen Fehler 1.Art und \(\beta\) die Wahrscheinlichkeit für einen Fehler 2.Art. Diese müssen in der Summe nicht 1 ergeben. Im besten Falle sind beide sehr gering, d.h. nahe an Null.
\(1 - \alpha\) entspricht der Wahrscheinlichkeit dafür, keine Fehlentscheidung zu treffen.
Falsch. Es gibt zwei Arten von Fehlentscheidungen, je nachdem, ob die \(H_{0}\) oder die \(H_{1}\) wahr ist. \(1 - \alpha\) entspricht lediglich der Wahrscheinlichkeit dafür, keinen Fehler 1. Art zu machen, falls die \(H_{0}\) wahr ist. Die Wahrscheinlichkeit für einen Fehler 2. Art, falls die \(H_{1}\) wahr ist, muss nicht gleich \(1 - \alpha\) sein.
Unter der Voraussetzung, dass \(X_{i}\) \(\stackrel{\text{iid}}{\sim} N\left( \mu,\sigma^{2} \right)\) für \(i = 1,\ 2,\ \ldots,\ n\), folgt die Zufallsvariable \[T = \frac{\overline{X} - \mu}{\sqrt{\frac{S^{2}}{n}}}\] einer t-Verteilung mit \(\nu = n - 1\).
Wahr. Siehe Vorlesung 7, Folie 56. Der tatsächliche Beweis ist sehr schwierig.
Unter der Voraussetzung, dass \(X_{i}\) \(\stackrel{\text{iid}}{\sim} N\left( \mu,\sigma^{2} \right)\) für \(i = 1,\ 2,\ \ldots,\ n\), folgt die Zufallsvariable \[T = \frac{\overline{X} - \mu_{0}}{\sqrt{\frac{S^{2}}{n}}}\] einer t-Verteilung mit \(\nu = n - 1\) . (Hinweis: \(\mu_{0}\) ist der konkrete, in der \(H_{0}\) angenommene Wert für \(\mu\))
Falsch. Diese Zufallsvariable folgt nur unter der Bedingung, dass die \(H_{0}:\mu = \mu_{0}\) wahr ist, einer t-Verteilung mit \(\nu = n - 1\). Dies ist der Grund dafür, dass wir sie als Teststatistik verwenden können. Falls \(\mu \neq \mu_{0}\) ist (also die \(H_{1}\) wahr ist), folgt die Zufallsvariable einer anderen Wahrscheinlichkeitsverteilung.
Falls wir uns im Rahmen eines statistischen Hypothesentests mit Signifikanzniveau \(\alpha = 0.005\) für die \(H_{1}\) entschieden haben, ist die Wahrscheinlichkeit für einen Fehler 2. Art gleich Null.
Falsch. Da wir uns für die \(H_{1}\) entschieden haben, ist es zwar unmöglich, dass wir uns in unserem konkreten Fall fälschlicherweise für die \(H_{0}\) entschieden haben. Wir können also keinen Fehler 2. Art gemacht haben. Das bedeutet aber nicht, dass die Wahrscheinlichkeit für einen Fehler 2. Art gleich Null ist. Dies hieße nämlich aufgrund der frequentistischen Interpretation der Wahrscheinlichkeit, dass wir uns, falls die \(H_{1}\) wahr wäre, bei unendlicher Wiederholung des statistischen Hypothesentests, in 0% der Fälle fälschlicherweise für die \(H_{0}\) entscheiden würden, also einen Fehler 2. Art machen würden. Dies können wir auf der Basis unserer einzelnen Testentscheidung nicht sagen.
Aus Ihrer Theorie ergibt sich, dass depressive PatientInnen, die sich einer von Ihnen entwickelten Psychotherapie unterziehen, eine mittlere (stetige) Depressionsschwere von ungleich 50 aufweisen sollten. Sie können davon ausgehen, dass das Histogramm der Depressionsschwere in der Population durch die Dichte einer Normalverteilung approximiert werden kann und eine einfache Zufallsstichprobe gezogen wird.
Stellen Sie die inhaltlichen Hypothesen auf.
\[H_{0}:{\overline{x}}_{D} = 50\]
\[H_{1}:{\overline{x}}_{D} \neq 50\]
Stellen Sie die statistischen Hypothesen auf.
\[H_{0}:\mu = 50\]
\[H_{1}:\mu \neq 50\]
Was wäre in diesem Fall ein Fehler 1. Art und was wäre ein Fehler 2. Art?
Fehler 1. Art: Wir entscheiden uns dafür, dass die mittlere Depressionsschwere in der Population der depressiven PatientInnen ungleich 50 ist, obwohl sie gleich 50 ist.
Fehler 2. Art: Wir entscheiden uns dafür, dass die mittlere Depressionsschwere in der Population der depressiven PatientInnen gleich 50 ist, obwohl sie ungleich 50 ist.
Geben Sie die Teststatistik an.
\[T = \frac{\overline{X} - \mu_{0}}{\sqrt{\frac{S^{2}}{n}}}\]
Geben Sie die Wahrscheinlichkeitsverteilung der Teststatistik unter der Voraussetzung, dass die \(H_{0}\) gilt, an.
t-Verteilung mit \(\nu = n - 1\).
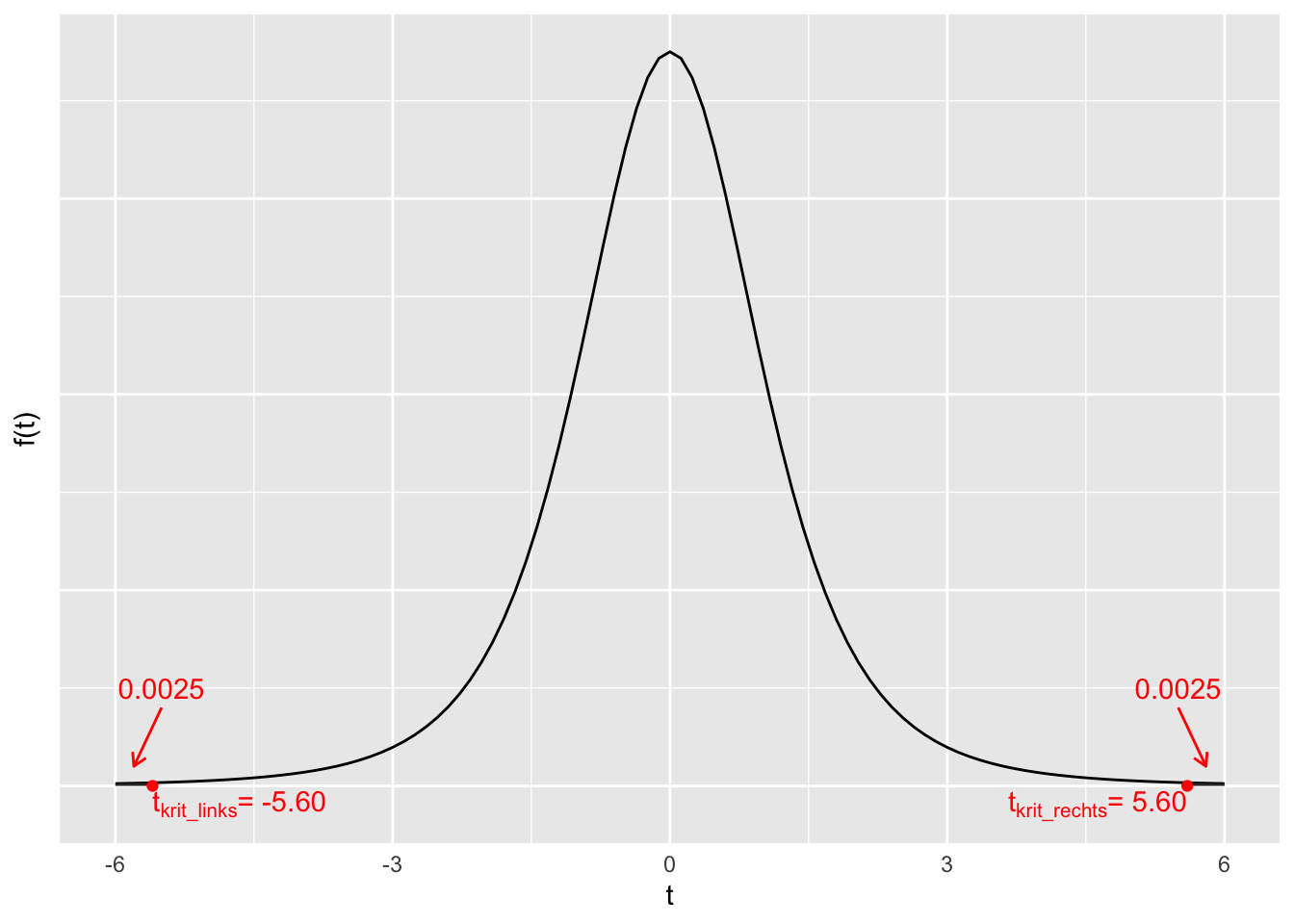
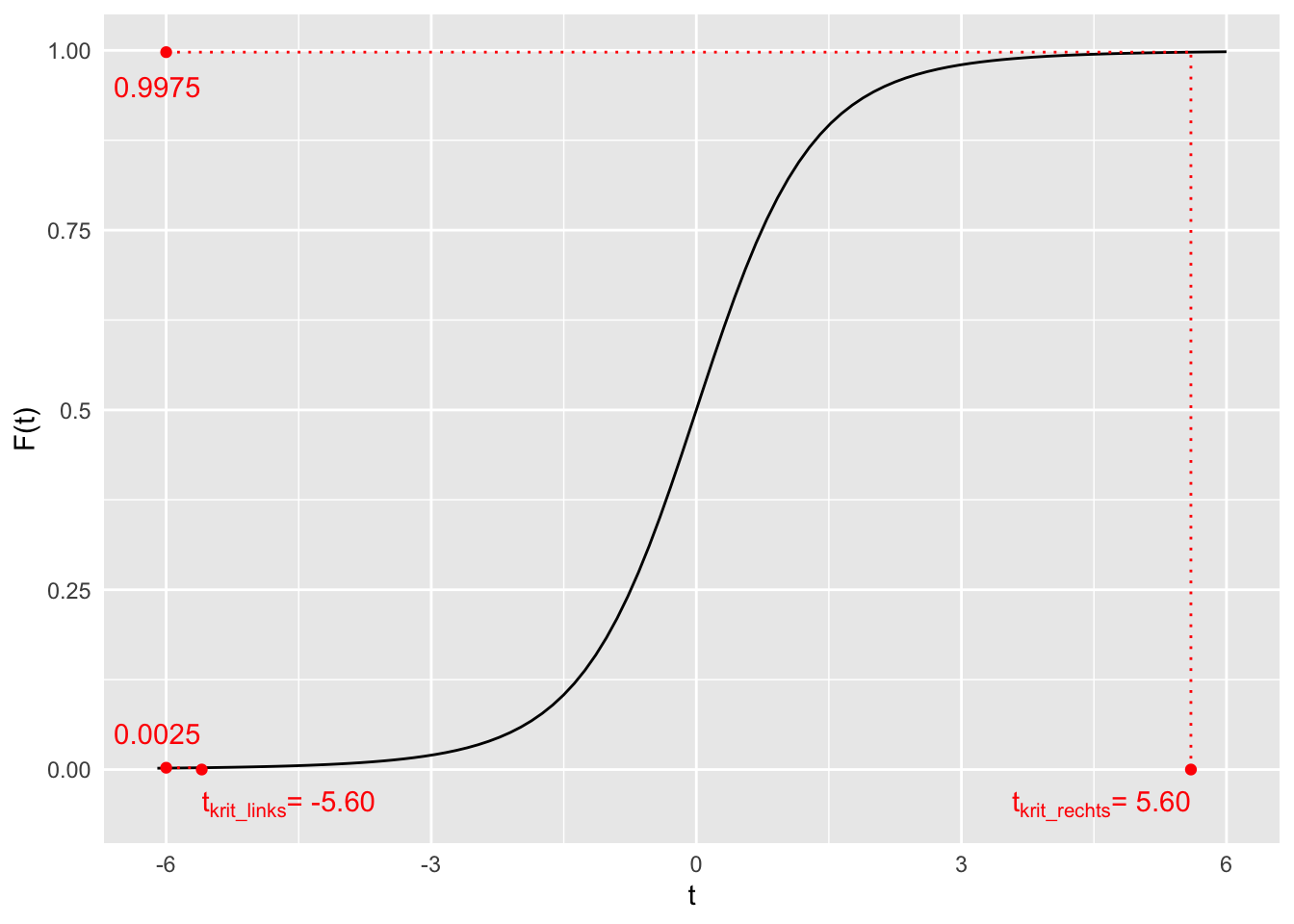
Bestimmen Sie die kritischen Werte für ein Signifikanzniveau von \(\alpha = 0.005\) mithilfe der qt-Funktion in R und veranschaulichen sie diese jeweils graphisch anhand der Verteilungsfunktion und der Wahrscheinlichkeitsdichtefunktion der Teststatistik unter der \(H_{0}\). (Hinweis: Die Stichprobengröße sei n = 5.)
\(\alpha = 0.005\)
Da wir fünf PatientInnen in unserer Stichprobe haben (siehe Teilaufgabe g), ist \(n = 5\) und daher \(\nu = n - 1 = 5 - 1 = 4\).
\(t_{krit\_ links}\ \)ist derjenige Wert, für den \(F\left( t_{krit\_ links} \right) = \frac{\alpha}{2} = \frac{0.005}{2} = 0.0025\) ist.
Berechnung in R:
Also ist \(t_{krit\_ links} \approx - 5.60\).
\(t_{krit\_ rechts}\ \)ist derjenige Wert, für den \(F\left( t_{krit\_ rechts} \right) = 1 - \frac{\alpha}{2} = 0.9975\) ist.
Aufgrund der Symmetrie der t-Verteilung um 0 gilt:
\(t_{krit\_ rechts} = - t_{krit_{links}} \approx - ( - 5.60) = 5.60\)
Graphische Veranschaulichung:
Sie haben folgende Daten aus einer einfachen Zufallsstichprobe vorliegen:
| PatientIn | Depressionsschwere |
|---|---|
| 1 | 40 |
| 2 | 45 |
| 3 | 56 |
| 4 | 50 |
| 5 | 55 |
Berechnen Sie die Realisation der Teststatistik.
Die Realisation der Teststatistik ist
\[t = \frac{\overline{x} - \mu_{0}}{\sqrt{\frac{s^{2}}{n}}}\]
\(\mu_{0} = 50\) ergibt sich aus unseren Hypothesen. Da wir fünf PatientInnen in unserer Stichprobe haben, ist \(n = 5\).
Wir müssen also noch \(\overline{x}\) und \(s^{2}\) berechnen.
\[\overline{x} = \frac{1}{n}\sum_{i = 1}^{n}x_{i} = \frac{40 + 45 + 56 + 50 + 55}{5} = 49.2\]
\[s^{2} = \frac{1}{n - 1}\sum_{i = 1}^{n}\left( x_{i} - \overline{x} \right)^{2} =\]
\[= \frac{(40 - 49.2)^{2} + (45 - 49.2)^{2} + (56 - 49.2)^{2} + (50 - 49.2)^{2} + (55 - 49.2)^{2}}{4} = 45.7\]
Einsetzen ergibt:
\[t = \frac{\overline{x} - \mu_{0}}{\sqrt{\frac{s^{2}}{n}}} = \frac{49.2 - 50}{\sqrt{\frac{45.7}{5}}} \approx - 0.26\]
Welche Testentscheidung treffen Sie? Begründen und interpretieren Sie diese.
Der kritische Bereich ist
\[K_{T} = \left\rbrack - \infty,\ t_{krit\_ links} \right\rbrack \cup \left\lbrack \ t_{krit\_ rechts},\infty \right\lbrack = \left\rbrack - \infty, - 5.60 \right\rbrack \cup \left\lbrack 5.60,\infty \right\lbrack\]
Da die Realisation der Teststatistik \(t = - 0.26\) nicht im kritischen Bereich liegt, entscheiden wir uns für die \(H_{0}\). Wir entscheiden uns also dafür, dass \({\overline{x}}_{D} = 50\) ist, also die mittlere Depressionsschwere in der Population der depressiven PatientInnen gleich 50 ist.
Was bedeutet Ihre Entscheidung für Ihre Theorie?
Aus der Theorie folgt, dass \({\overline{x}}_{D} \neq 50\) sein müsste, wir haben uns im Rahmen unseres statistischen Hypothesentests aber für \({\overline{x}}_{D} = 50\) entschieden. Dies spricht also gegen unsere Theorie.