Übungsblatt 11

Einführung in statistische Hypothesentests II

  1. R-Code für die verschiedenen Hypothesentests:

    Verwenden Sie für alle t-Tests die t.test Funktion.

    Eine Stichprobe: t.test(Messwerte, alternative, mu)

    Zwei Stichproben: t.test(MesswerteStichprobe1, MesswerteStichprobe2, alternative, mu, paired, var.equal = TRUE)

    In dem Argument alternative spezifizieren Sie die Richtung der Alternativhypothese:

    alternative = „two.sided" für eine ungerichtete Alternativhypothese,

    alternative = „less" für eine linksgerichtete Alternativhypothese,

    alternative = „greater" für eine rechtsgerichtete Alternativhypothese.

    mu ist der Wert \(\mu_{0}.\)

    paired = TRUE für abhängige Stichproben,

    paired = FALSE für unabhängige Stichproben.

    Achten Sie bei zwei Stichproben und gerichteten Alternativhypothesen auf die Reihenfolge der Vektoren, die die Messwerte enthalten:

    Der Befehl t.test(MesswerteStichprobe1, MesswerteStichprobe2, alternative = „less", mu = 0, paired = FALSE, var.equal=TRUE)

    berechnet den p-Wert für die Hypothesen

    \[H_{0}:\ \mu_{1} - \mu_{2} \geq 0\] \[H_{1}:\ \mu_{1} - \mu_{2} < 0\]

    wohingegen der Befehl t.test(MesswerteStichprobe2, MesswerteStichprobe1, alternative = „less", mu = 0, paired = FALSE, var.equal=TRUE)

    den p-Wert für die Hypothesen

    \[H_{0}:\ \mu_{2} - \mu_{1} \geq 0\] \[H_{1}:\ \mu_{2} - \mu_{1} < 0\]

    berechnet.

    Verwenden Sie für den Binomialtest die binom.test Funktion:

    binom.test(x, n, p, alternative)

    x ist die absolute Häufigkeit der interessierenden Messwertausprägung in der Stichprobe, d.h. die Realisation der Teststatistik. Diese müssen Sie unter Umständen zunächst mithilfe der table Funktion selbst berechnen.

    n ist die Stichprobengröße.

    p ist der Wert \(\pi_{0}\).

    In dem Argument alternative spezifizieren Sie die Richtung der Alternativhypothese:

    alternative = „two.sided" für eine ungerichtete Alternativhypothese,

    alternative = „less" für eine linksgerichtete Alternativhypothese,

    alternative = „greater" für eine rechtsgerichtete Alternativhypothese.

  1. Sie vermuten, dass der Anteil von Personen ohne Abitur an den unter Depression leidenden Personen größer ist als der Anteil der Personen mit Abitur. Sie ziehen eine einfache Zufallsstichprobe der Größe \(n = 400\) aus der Population der Depressiven und erfassen von jeder Person den höchsten Bildungsabschluss, um diese Hypothese zu überprüfen. Sie wählen ein Signifikanzniveau von \(\alpha = 0.005\).

    1. Stellen Sie die inhaltlichen Hypothesen auf.

      \[H_{0}:\ h_{ohne\_ Abitur} \leq 0.5\]

      \[H_{1}:\ h_{ohne\_ Abitur} > 0.5\]

    2. Stellen Sie die statistischen Hypothesen auf.

      \[H_{0}:\ \pi \leq 0.5\]

      \[H_{1}:\ \pi > 0.5\]

    3. Welchen statistischen Hypothesentest wählen Sie zur Überprüfung dieser Hypothesen?

      Binomialtest für (rechts-)gerichtete Hypothesen.

    4. In Ihrer Stichprobe befinden sich 169 Personen mit Abitur und 231 ohne Abitur. Berechnen Sie den p-Wert zunächst selbst mithilfe der pbinom Funktion. Überprüfen Sie Ihr Ergebnis dann, indem Sie den p-Wert mit der Funktion in R für den entsprechenden Hypothesentest berechnen.

      Die Realisation \(t\) der Teststatistik \(T\) entspricht der absoluten Häufigkeit der Personen ohne Abitur in der Stichprobe, da sich die inhaltlichen Hypothesen auf die relative Häufigkeit der Personen ohne Abitur in der Population beziehen.

      Die Realisation der Teststatistik \(T\) ist somit \(t = 231\).

      Da wir eine rechtsseitige Alternativhypothese haben, ist der p-Wert

      \(P(T \geq t) = P(T \geq 231) = 1 - P(T < 231) = 1 - P(T \leq 230) = 1 - F(230)\),

      wobei \(P\) eine Binomialverteilung mit \(n = 400\) und \(\pi = \pi_{0} = 0.5\)und \(F\) deren Verteilungsfunktion ist.

      Berechnung mithilfe von pbinom in R:

      1 - pbinom(230, 400, 0.5)
      [1] 0.001124104

      Überprüfung mit binom.test:

      binom.test(231, 400, 0.5, alternative = 'greater')
      
    Exact binomial test

data:  231 and 400
number of successes = 231, number of trials = 400, p-value = 0.001124
alternative hypothesis: true probability of success is greater than 0.5
95 percent confidence interval:
 0.5352962 1.0000000
sample estimates:
probability of success 
                0.5775

    5. Welche Testentscheidung treffen Sie? Begründen und interpretieren Sie diese.

      Da \(p = 0.001 \leq 0.005 = \alpha\) ist, entscheiden wir uns für die \(H_{1}\). Wir entscheiden uns also dafür, dass der Anteil der Personen ohne Abitur an den unter einer Depression leidenden Personen größer ist als der Anteil der Personen mit Abitur.

  1. Der d2 Test ist ein psychologischer Test, der zur Beurteilung der Konzentration eingesetzt wird. Er besteht aus 14 Items, welche jeweils aus 57 Zeichen bestehen. Pro Zeile hat die Person 20 Sekunden Zeit, alle d’s mit zwei Strichen zu markieren. Nachfolgend wird ein Ausschnitt aus einem d2 Test gezeigt:

    Unter anderem kann bei dem Test die Anzahl der richtig bearbeiteten Zeichen als Maß für die Konzentration verwendet werden.

    Sie vermuten, dass die mittlere (stetige) Konzentrationsleistung von Personen morgens höher ist als abends. Sie können davon ausgehen, dass das Histogramm der Konzentrationsfähigkeit in der Population sowohl morgens als auch abends durch die Dichte einer Normalverteilung approximiert werden kann und eine einfache Zufallsstichprobe (n=121) von Personen gezogen wird, die alle einmal morgens und einmal abends den d2 Test machen müssen. Sie legen das Signifikanzniveau auf \(\alpha = 0.005\) fest.

    Laden Sie den Datensatz herunter und lesen Sie ihn in R als Objekt mit dem Namen daten ein.

    1. Stellen Sie die inhaltlichen Hypothesen auf.

      \[H_{0}:\ {\overline{x}}_{Pop\_ morgens} - {\overline{x}}_{Pop\_ abends} \leq 0\]

      \[H_{1}:\ {\overline{x}}_{Pop\_ morgens} - {\overline{x}}_{Pop\_ abends} > 0\]

    2. Stellen Sie die statistischen Hypothesen auf.

      \[H_{0}:\ \mu_{morgens} - \mu_{abends} \leq 0\]

      \[H_{1}:\ \mu_{morgens} - \mu_{abends} > 0\]

    3. Welchen statistischen Hypothesentest wählen Sie zur Überprüfung dieser Hypothesen?

      Zweistichproben t-Test für gerichtete Hypothesen und abhängige Stichproben.

    4. Berechnen Sie den p-Wert in R mithilfe der Funktion für den entsprechenden Hypothesentest.

      daten <- read.csv2('d2.csv')

t.test(daten$morgens, daten$abends, alternative = 'greater', mu = 0, paired = TRUE, var.equal = TRUE)
      
    Paired t-test

data:  daten$morgens and daten$abends
t = 6.5294, df = 120, p-value = 8.318e-10
alternative hypothesis: true mean difference is greater than 0
95 percent confidence interval:
 17.11154      Inf
sample estimates:
mean difference 
       22.93388

      Der p-Wert ist 0.0000000008318.

    5. Welche Testentscheidung treffen Sie? Begründen und interpretieren Sie diese.

      Da \(p = 0.0000000008318 \leq 0.005 = \alpha\) ist, entscheiden wir uns für die \(H_{1}\). Wir entscheiden uns also dafür, dass die mittlere Konzentrationsleistung von Personen morgens höher ist als abends.

  1. Die durchschnittliche Abiturnote in Deutschland beträgt 2.5. Sie wollen nun überprüfen, ob Schüler:innen, morgens regelmäßig ein Glas Tomatensaft trinken, im Mittel bessere Abiturnoten als der Bundesdurchschnitt bekommen. Zu diesem Zweck erheben Sie eine einfache Zufallsstichprobe von Tomatensaft trinkenden Schüler:innen, die im letzten Schuljahr Abitur geschrieben haben (Stichprobengrößen = 10000) und erfassen deren Abiturnote. Sie können davon ausgehen, dass das Histogramm der Abiturnote in der Population Tomatensaft trinkender Schüler:innen durch die Dichte einer Normalverteilung approximiert werden kann. Das Signifikanzniveau sei \(\alpha = 0.005\).

    Laden Sie den Datensatz herunter und lesen Sie ihn in R als Objekt unter dem Namen tomaten ein.

    1. Stellen Sie die inhaltlichen Hypothesen auf.

      \[H_{0}:\ {\overline{x}}_{Pop\_ Tomaten} \geq 2.5\]

      \[H_{1}:\ {\overline{x}}_{Pop\_ Tomaten} < 2.5\]

    2. Stellen Sie die statistischen Hypothesen auf.

      \[H_{0}:\ \mu \geq 2.5\]

      \[H_{1}:\ \mu < 2.5\]

    3. Welchen statistischen Hypothesentest wählen Sie zur Überprüfung dieser Hypothesen?

      Einstichproben t-Test für gerichtete Hypothesen.

    4. Berechnen Sie den p-Wert in R mithilfe der Funktion für den entsprechenden Hypothesentest.

      tomaten <- read.csv2('tomaten.csv')

t.test(tomaten$abinote, alternative = 'less', mu = 2.5)
      
    One Sample t-test

data:  tomaten$abinote
t = -4.4451, df = 9999, p-value = 4.441e-06
alternative hypothesis: true mean is less than 2.5
95 percent confidence interval:
     -Inf 2.483408
sample estimates:
mean of x 
  2.47366

      Der p-Wert ist 0.000004441.

    5. Welche Testentscheidung treffen Sie? Begründen und interpretieren Sie diese.

      Da \(p = 0.000004441 \leq 0.005 = \alpha\) ist, entscheiden wir uns für die \(H_{1}\). Wir entscheiden uns also dafür, dass Schüler:innen, die morgens regelmäßig ein Glas Tomatensaft trinken, im Mittel bessere Abiturnoten als der Bundesdurchschnitt bekommen.

    6. Würden Sie auf der Basis dieser Ergebnisse Ihre eigenen Kinder vor dem Abitur jeden Morgen Tomatensaft trinken lassen?

      Eine solche Entscheidung kann auf der Basis des vorliegenden Hypothesentests nicht getroffen werden, da lediglich getestet wurde, ob die durchschnittliche Abiturnote in der Population der Tomatensaft trinkenden Schüler:innen kleiner als der Bundesdurchschnitt ist. Kausale Schlüsse im Sinne von „Tomatensaft führt zu besseren Abiturnoten” können nicht gezogen werden.

      Aber auch wenn dies möglich wäre (z.B. wenn es sich um experimentelle Daten handeln würde), sollte man berücksichtigen, dass der tatsächliche Schätzwert sich nur minimal von 2.5 unterscheidet. Trotzdem entscheiden wir uns im Rahmen des statistischen Hypothesentests für die H1, da statistische Hypothesentests mit zunehmender Stichprobengröße immer „genauer” werden und auch sehr kleine Abweichungen erkennen. Eine statistisch signifikante Abweichung muss aber nicht unbedingt eine große Abweichung sein.

  2. Sie vermuten, dass 18-jährige Personen sich in der mittleren (stetigen) Konzentrationsleistung von 65-jähigen Personen unterscheiden. Sie verwenden als Erhebungsinstrument den d2-Test. Sie können davon ausgehen, dass das Histogramm der Konzentrationsleistung in beiden Populationen jeweils durch die Dichte einer Normalverteilung approximiert werden kann und dass die empirische Varianz in beiden Populationen gleich ist. Sie haben die folgenden Daten aus zwei unabhängigen einfachen Zufallsstichproben vorliegen. Das Signifikanzniveau sei \(\alpha = 0.005\).

    Konzentrationsleistung im d2-Test
    (18-jährige)    		 Konzentrationsleistung im d2-Test
    (65-jährige)
    210 215
    225 151
    199 158
    252 283
    208 168
    266 177
    154 173
    300

    1. Stellen Sie die inhaltlichen Hypothesen auf.

      \[H_{0}:\ {\overline{x}}_{Pop\_ 18} - {\overline{x}}_{Pop\_ 65} = 0\]

      \[H_{1}:\ {\overline{x}}_{Pop\_ 18} - {\overline{x}}_{Pop\_ 65} \neq 0\]

    2. Stellen Sie die statistischen Hypothesen auf.

      \[H_{0}:\ \mu_{18} - \mu_{65} = 0\]

      \[H_{1}:\ \mu_{18} - \mu_{65} \neq 0\]

    3. Welchen statistischen Hypothesentest wählen Sie zur Überprüfung dieser Hypothesen?

      Zwei-Stichproben t-Test für ungerichtete Hypothesen und unabhängige Stichproben.

    4. Berechnen Sie die Realisation der Teststatistik per Hand.

      Der Index 1 steht im Folgenden für die Stichprobe der 18-Jährigen und der Index 2 für die Stichprobe der 65-Jährigen.

      \[n_{1} = 8\]

      \[n_{2} = 7\]

      \[{\overline{x}}_{1} = 226.75\]

      \[{\overline{x}}_{2} = 189.29\]

      \[s_{1}^{2} = 2034.50\]

      \[s_{2}^{2} = 2126.24\]

      \[s_{pool}^{2} = \frac{\left( n_{1} - 1 \right) \cdot s_{1}^{2} + \left( n_{2} - 1 \right) \cdot s_{2}^{2}}{n_{1} + n_{2} - 2} = \frac{7 \cdot 2034.50 + 6 \cdot 2126.24}{13} = 2076.84\]

      \[t = \frac{{(\overline{x}}_{1} - {\overline{x}}_{2}) - \mu_{0}}{\sqrt{\frac{S_{pool}^{2}}{n_{1}} + \frac{S_{pool}^{2}}{n_{2}}}} = \frac{(226.75 - 189.29) - 0}{\sqrt{\frac{2076.84}{8} + \frac{2076.84}{7}}} = 1.59\]

    5. Berechnen Sie den p-Wert mithilfe der pt Funktion.

      Da wir eine ungerichtete Alternativhypothese haben und \(t = 1.59 > 0\) ist, ist der p-Wert

      \[P\left( T \leq - t\text{~oder~}T \geq t \right) = P\left( T \leq - t\text{~} \right) + P(T \geq t) = P\left( T \leq - 1.59\text{~} \right) + P(T \geq 1.59)\]

      \[= 2 \cdot P(T \leq - 1.59) = 2 \cdot F( - 1.59)\]

      wobei \(P\) eine t-Verteilung mit \(\nu = n_{1} + n_{2} - 2 = 13\) und \(F\) deren Verteilungsfunktion ist.

      Berechnung mithilfe von pt in R:

      2 * pt(-1.59, 13)
      [1] 0.1358493

    6. Veranschaulichen Sie den ermittelten p-Wert und die Realisation der Teststatistik mithilfe der entsprechenden Dichtefunktion graphisch. Beschriften Sie dabei die Achsen und versehen Sie die Skizze mit einer Überschrift.

      Wahrscheinlichkeitsdichte der Teststatistik \(T\) unter der Annahme, dass die \(H_{0}\) gilt.

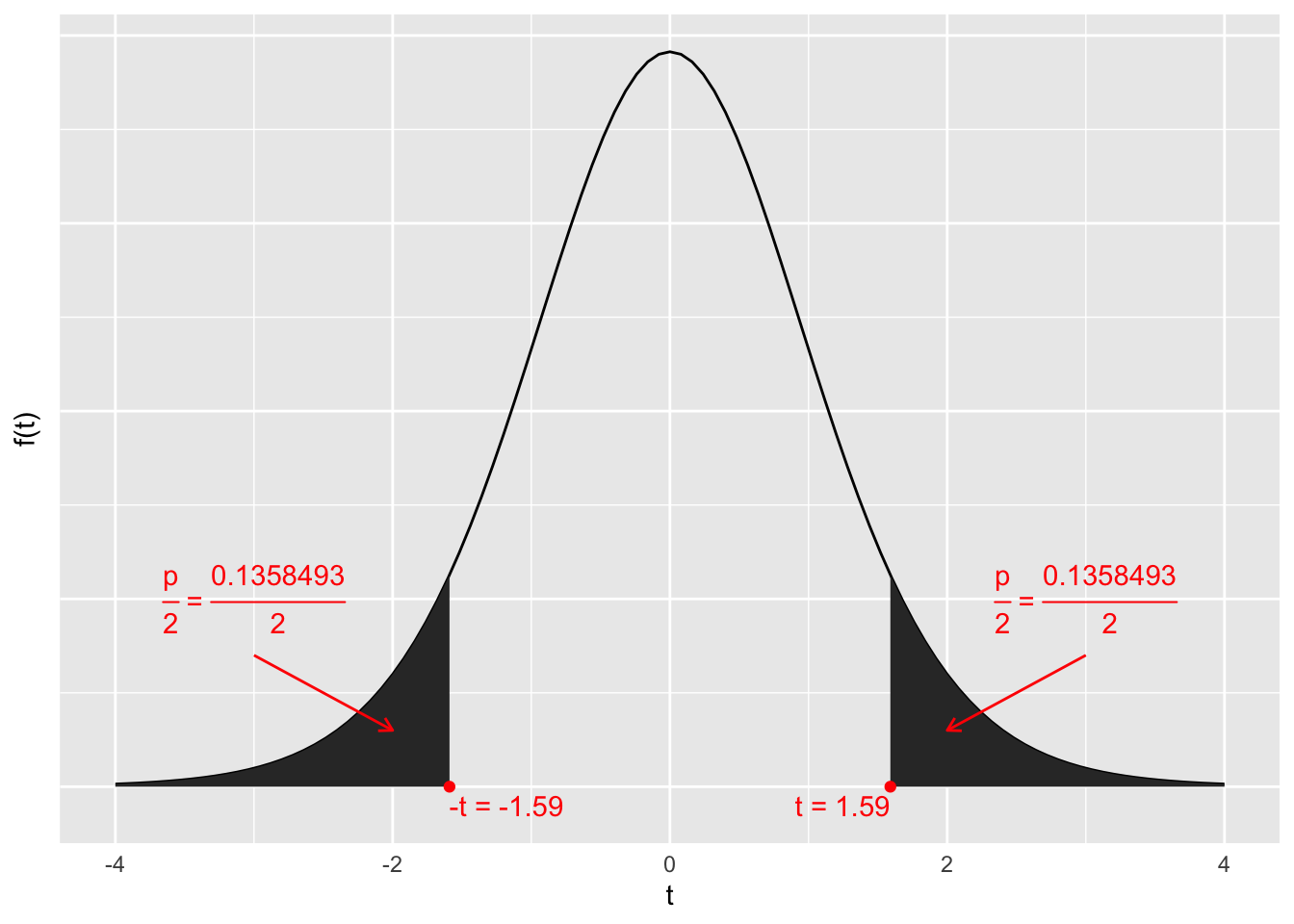
    7. Welche Testentscheidung treffen Sie? Begründen und interpretieren Sie diese.

      Da \(p = 0.1358493 > 0.005 = \alpha\) ist, entscheiden wir uns für die \(H_{0}\). Wir entscheiden uns also dafür, dass 18-jährige Personen sich in der mittleren Konzentrationsleistung von 65-jähigen Personen nicht unterscheiden.

    8. Warum können Sie das Testergebnis in Frage stellen?

      Sehr kleine Stichprobe, daher vermutlich geringe Power.