Übungsblatt 12

Effektstärken, Power und Stichprobenplanung

R-Code für Konfidenzintervalle für $\mathbf{\delta}$ und Stichprobenplanung für Konfidenzintervalle:

Die Funktionen für die Konfidenzintervalle für $\delta$ sind im MBESS package enthalten.
Berechnung des Konfidenzintervalls für unabhängige Stichproben:
ci.smd(smd, n.1, n.2, conf.level)
- In dem Argument smd geben Sie den Schätzwert für $\delta$ an. Diesen müssen Sie vorher berechnen.
- n.1 ist die Größe der Stichprobe 1.
- n.2 ist die Größe der Stichprobe 2.
- conf.level ist das gewünschte Konfidenzniveau.
Wichtig: Sie müssen alle Argumente explizit mit dem jeweiligen Namen und = angeben,

d.h. z.B.

ci.smd(smd = 0.2, n.1 = 100, n.2 = 80, conf.level = 0.95)

statt

ci.smd(0.2, 100, 80, 0.95).
Berechnung des Konfidenzintervalls für abhängige Stichproben:
ci.sm(sm, N, conf.level)
- In dem Argument sm geben Sie den Schätzwert für $\delta$ an. Diesen müssen Sie vorher berechnen.
- N ist die Größe der Stichprobe pro Messzeitpunkt.
- conf.level ist das gewünschte Konfidenzniveau.
Wichtig: Sie müssen alle Argumente explizit mit dem jeweiligen Namen und = angeben.
Stichprobenplanung für unabhängige Stichproben:
ss.aipe.smd(delta, conf.level, width)
- delta ist das $\delta$, von dem Sie ausgehen.
- conf.level ist das gewünschte Konfidenzniveau.
- width ist die gewünschte erwartete Länge des Konfidenzintervalls.
Wichtig: Sie müssen alle Argumente explizit mit dem jeweiligen Namen und = angeben.
Stichprobenplanung für abhängige Stichproben:
ss.aipe.sm(sm, conf.level, width)
- sm ist das $\delta$, von dem Sie ausgehen.
- conf.level ist das gewünschte Konfidenzniveau.
- width ist die gewünschte erwartete Länge des Konfidenzintervalls.
Wichtig: Sie müssen alle Argumente explizit mit dem jeweiligen Namen und = angeben.
R-Code für Poweranalyse und Stichprobenplanung bei Hypothesentests:

Die Funktionen für die Poweranalysen sind im pwr package enthalten. Dieses müssen sie installieren und laden.
Poweranalyse t-Tests:
pwr.t.test(n, d, sig.level, type, alternative)
- n ist die Stichprobengröße pro Stichprobe:
  
  Bei Einstichproben t-Tests entspricht dies einfach der Stichprobengröße.
  
  Bei Zweistichproben t-Tests für abhängige Stichproben entspricht dies der Stichprobengröße pro Messzeitpunkt.
  
  Bei Zweistichproben t-Tests für unabhängige Stichproben entspricht dies der Stichprobengröße pro Stichprobe (also $n_{1}$ bzw. $n_{2}$). Das heißt, Sie können die Power nur für gleiche Stichprobengrößen $n_{1} = n_{2}$ bestimmen.
- d ist der Effekt unter der $H_{1}$ , für den Sie die Power berechnen wollen. Wichtig: Muss bei linksgerichteten Alternativhypothesen ein negatives Vorzeichen haben!
- sig.level ist das Signifikanzniveau des Hypothesentests.
- type ist die Art des t-Tests:
  
  „one.sample" für einen Einstichproben t-Test.
  
  „two.sample" für einen Zweistichproben t-Test für unabhängige Stichproben.
  
  „paired" für einen Zweistichproben t-Test für abhängige Stichproben.
- alternative ist die Richtung der Alternativhypothese:
  
  „two.sided" für ungerichtete Alternativhypothesen.
  
  „less" für linksgerichtete Alternativhypothesen.
  
  „greater" für rechtsgerichte Alternativhypothesen.
Wichtig: Sie müssen alle Argumente explizit mit dem jeweiligen Namen und = angeben.
Stichprobenplanung t-Tests:
pwr.t.test(power, d, sig.level, type, alternative)

Gleiche Funktion wie bei der Poweranalyse, aber mit dem Argument power statt dem Argument n.
- power gibt die gewünschte Power an.
Wichtig: Sie müssen alle Argumente explizit mit dem jeweiligen Namen und = angeben.

Wir betrachten das Tomatenbeispiel aus dem letzten Übungsblatt (Aufgabe 3).
1. Berechnen Sie für den dort verwendeten Hypothesentest die Power unter der Annahme eines sehr kleinen Effekts ($|\delta_{H_{1}}| = 0.05$).
  Lösung
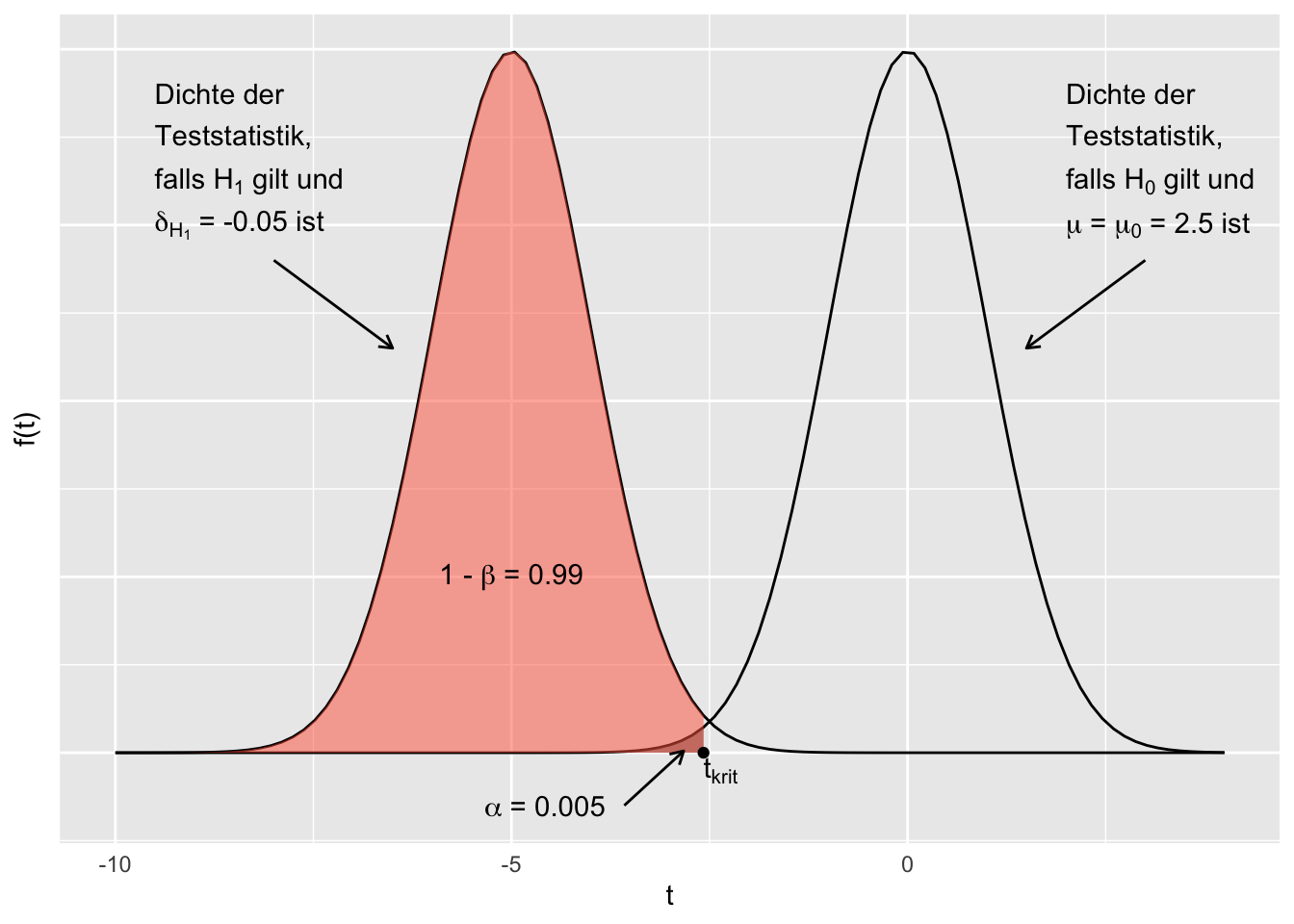
  library(MBESS) library(pwr) pwr.t.test(n = 10000, d = -0.05, sig.level = 0.005, type = 'one.sample', alternative = 'less')
  
  One-sample t test power calculation n = 10000 d = -0.05 sig.level = 0.005 power = 0.9923108 alternative = less
  
  Die Power ist in diesem Fall 0.99 und damit sehr hoch.
2. Veranschaulichen Sie das Signifikanzniveau und die Power des Hypothesentests unter diesen Voraussetzungen graphisch anhand der Dichtefunktionen der Teststatististik unter der Voraussetzung $\mu = \mu_{0}$ unter der $H_{0}$ und unter der Voraussetzung eines wahren Effekts $\delta_{H_{1}}$ unter der $H_{1}$.
  
  Lösung
3. Nehmen Sie Stellung zu folgender Aussage: „Die Stichprobe ist mit n = 10000 zu groß. Dies führt dazu, dass der verwendete Hypothesentest eine viel zu hohe Power hat und daher auch bei praktisch irrelevanten Unterschieden mit hoher Wahrscheinlichkeit zu einer Entscheidung für die $H_{1}$ führt. Es wäre daher sinnvoll gewesen, eine kleinere Stichprobe zu erheben.”
  
  Lösung
  
  Diese Aussage ergibt keinen Sinn. Es ist unmöglich, eine zu große Stichprobe zu erheben. Die Power ist ein zentrales Gütekriterium statistischer Hypothesentests und kann in keinem Fall zu hoch sein. Falls man Unterschiede erst ab einem bestimmten Wert für praktisch relevant hält, sollte man die Hypothesen anders formulieren. In dem Tomatensaftbeispiel könnte man statt
  
  \[H_{0}:\mu \geq 2.5\]
  
  \[H_{1}:\mu < 2.5\]
  
  die Hypothesen
  
  \[H_{0}:\mu \geq 2\]
  
  \[H_{1}:\mu < 2\]
  
  aufstellen, falls man einen Unterschied in der mittleren Abiturnote zwischen tomatensafttrinkenden Schüler:innen und der Gesamtpopulation erst ab 0.5 für relevant hält.
In einem (fiktiven) wissenschaftlichen Artikel zu Unterschieden in der Gewissenhaftigkeit zwischen Studierenden verschiedener Fachrichtungen finden Sie folgende Textstellen:

Methodenteil:

„Zur Überprüfung unserer Hypothese, dass Studierende der VWK eine höhere Gewissenhaftigkeit aufweisen als Studierende der BWL, erhoben wir jeweils eine zufällige Stichprobe von VWL Studierenden (n = 10000) und eine zufällige Stichprobe von BWL Studierenden (n = 10000).”

Ergebnisteil:

„Die durchschnittliche Gewissenhaftigkeit in der Stichprobe der BWL Studierenden betrug 100.3 (SD = 14.9), während die durchschnittliche Gewissenhaftigkeit in der Stichprobe der VWL Studierenden 100.7 betrug (SD = 15.4). Zur Überprüfung der Hypothesen wurde ein t-Test für unabhängige Stichproben mit gerichteter Alternativhypothese und $\alpha = 0.05$ durchgeführt. Dieser lieferte folgende Ergebnisse: t = 1.87, df = 19998, p = 0.03”

Diskussionsteil:

„Unsere Studie ist die bislang größte und aufwendigste Studie zu Unterschieden in der Gewissenhaftigkeit zwischen Studierenden verschiedener Fachrichtungen. In den Daten zeigte sich ein signifikanter Unterschied in der Gewissenhaftigkeit zwischen Studierenden der VWL und Studierenden der BWL (p = 0.03). Die Hypothese, dass VWL Studierende gewissenhafter sind als BWL Studierende, konnte dadurch eindrucksvoll bestätigt werden.”

Hinweis: In wissenschaftlichen Artikeln wird $s = \sqrt{s^{2}}$ oft SD genannt.
1. Berechnen Sie ein 95%-Konfidenzintervall für den Unterschied in der durchschnittlichen Gewissenhaftigkeit zwischen VWL und BWL Studierenden.
  
  Lösung
  
  \[I\left( x_{1},\ldots,x_{20000} \right) =\]
  
  \[= \left\lbrack (100.7 - 100.3) - 1.96 \cdot \sqrt{2 \cdot \frac{229.59}{10000}},(100.7 - 100.3) + 1.96 \cdot \sqrt{2 \cdot \frac{229.59}{10000}} \right\rbrack\]
  
  \[= \lbrack 0,4 - 1.96 \cdot 0.21,\ 0.4 + 1.96 \cdot 0.21\rbrack = \lbrack - 0.02,\ 0.82\rbrack\]
  
  wobei $s_{pool}^{2} = \frac{{14,9}^{2} + {15,4}^{2}}{2} = 229.59$
2. Berechnen Sie den Schätzwert für Cohen’s $\delta$.
  
  Lösung
  
  \[{\widehat{\delta}}_{Wert} = \frac{{\overline{x}}_{m} - {\overline{x}}_{w}}{\sqrt{s_{pool}^{2}}} = \frac{100.7 - 100.3}{\sqrt{229.59}} \approx 0.03\]
3. Berechnen Sie das 95%-Konfidenzintervall für Cohen’s $\delta$. Interpretieren Sie das resultierende Konfidenzintervall und diskutieren Sie die Schlussfolgerung der Autor:innen der Studie.
  Lösung
  ci.smd(smd = 0.03, n.1 = 10000, n.2 = 10000, conf.level = 0.95)
  
  $Lower.Conf.Limit.smd [1] 0.002279989 $smd [1] 0.03 $Upper.Conf.Limit.smd [1] 0.05771926
  
  Interpretation: Auf Basis der Daten liegen die plausiblen Werte für $\delta$ im Bereich von 0.00 bis 0.06. Dies spricht sehr stark dafür, dass die Gewissenhaftigkeitsunterschiede zwischen VWL und BWL Studierenden vernachlässigbar klein sind.
  
  Diskussion: Die Autor:innen begehen den Fehler, ausschließlich das Ergebnis des Hypothesentests zu interpretieren. Vor allem bei großen Stichproben kann dies zu Fehlschlüssen führen, da der Hypothesentest dann auch minimale und praktisch nicht bedeutsame Abweichungen von der Nullhypothese erkennt (vgl. auch Tomatensaftbeispiel). Deshalb sollte bei großen Stichproben immer auch das Konfidenzintervall für den interessierenden Parameter betrachtet werden. Ist die ursprüngliche Einheit des Merkmals schwer interpretierbar (wie bei der Gewissenhaftigkeit), sollte zusätzlich das Konfidenzintervall für eine geeignete Effektstärke betrachtet werden.
In einer Fachzeitschrift werden folgende Untersuchungsergebnisse veröffentlicht, die auf der Durchführung eines t-Tests für unabhängige Stichproben basieren:

\[H_{0}:\mu_{1} - \mu_{2} = 0\]

\[H_{1}:\mu_{1} - \mu_{2} \neq 0\]

\[{\widehat{\delta}}_{Wert} = 0.69\]

\[p = 0.041\]

\[n_{1} = n_{2} = 18\]

\[\alpha = 0.05\]

Die Autor:innen der Studie interpretieren im Diskussionsteil des Fachartikels ihre Ergebnisse als Beleg für einen signifikanten mittleren bis großen Effekt.
1. Welche Argumente sprechen gegen diese Sichtweise? Belegen Sie Ihre Argumentation mit einer entsprechenden Analyse.
  Lösung
  Die Autor:innen berichten und interpretieren lediglich einen Punktschätzwert für $\delta$. Die beiden Stichproben sind extrem klein, so dass das Konfidenzintervall zum 95%- Konfidenzniveau für $\delta\ $zu breit ist, um eine Aussage über die Größe des Mittelwertunterschieds treffen zu können. Berechnung des Konfidenzintervalls:
  
  ci.smd(smd = 0.69, n.1 = 18, n.2 = 18, conf.level = 0.95)
  
  $Lower.Conf.Limit.smd [1] 0.01179104 $smd [1] 0.69 $Upper.Conf.Limit.smd [1] 1.358675
2. Berechnen Sie, wie groß die Stichprobe mindestens sein müsste, um zwischen kleinen, mittleren und großen Effekten im Sinne von Cohen differenzieren zu können. Legen Sie der Berechnung $\delta = 0.5$ zugrunde.
  Lösung
  ss.aipe.smd(delta = 0.5, conf.level = 0.95, width = 0.29)
  
  [1] 377
  
  In jeder der beiden Stichproben müssten 377 Personen erhoben werden.
3. Welche Auswirkungen hätte es, wenn das wahre $\delta$ größer als 0.5 wäre und Sie eine Stichprobe mit der auf der Basis von $\delta = 0.5$ berechneten Größe erheben würden?
  
  Lösung
  
  Die erwartete Länge des Konfidenzintervalls wäre größer als die gewünschte Länge.
4. Welche Auswirkungen hätte es, wenn das wahre $\delta$ kleiner als 0.5 wäre und Sie eine Stichprobe mit der auf der Basis von $\delta = 0.5$ berechneten Größe erheben würden?
  
  Lösung
  
  Die erwartete Länge des Konfidenzintervalls wäre kleiner als die gewünschte Länge.
Sie planen eine Studie, die den Einfluss der Wunschuniversität auf den Studienerfolg untersucht. Sie vermuten, dass Studierende die nicht an ihrer Wunschuniversität studieren im Mittel schlechtere Noten haben als Studierende die an ihrer Wunschuniversität studieren. Bisherige Ergebnisse zeigen, dass von einem kleinen Populationseffekt auszugehen ist. Sie legen daher den Effekt unter der $H_{1}$ auf $\delta_{H_{1}} = 0.2$ fest. Die Untersuchung soll mithilfe eines t-Tests für unabhängige Stichproben durchgeführt werden, der folgende Eigenschaften aufweisen soll: $\alpha = 0.005$, $1 - \beta = 0.8$.
1. Ermitteln Sie den notwendigen Mindeststichprobenumfang.
  Lösung
  pwr.t.test(power = 0.8, d = 0.2, sig.level = 0.005, type = 'two.sample', alternative = 'greater')
  
  Two-sample t test power calculation n = 585.6093 d = 0.2 sig.level = 0.005 power = 0.8 alternative = greater NOTE: n is number in *each* group
  
  Es werden 586 Studierende in jeder der beiden Stichproben benötigt. Insgesamt benötigen Sie also 586 + 586 = 1172 Studierende.
2. Wie hoch wäre die Power Ihres Tests im Vergleich zu $1 - \beta = 0.8$ für den berechneten Stichprobenumfang, falls die $H_{1}$ gelten würde und ein größerer Effekt als $\delta_{H_{1}} = 0.2$ vorliegen würde?
  
  Lösung
  
  Die Power wäre in diesem Fall größer als 0.8.
3. Wie hoch wäre die Power Ihres Tests im Vergleich zu $1 - \beta = 0.8$ für den berechneten Stichprobenumfang, falls die $H_{1}$ gelten würde und ein kleinerer Effekt als $\delta_{H_{1}} = 0.2$ vorliegen würde?
  
  Lösung
  
  Die Power wäre in diesem Fall kleiner als 0.8.
4. Wie hoch wäre die Power Ihres Tests im Vergleich zu $1 - \beta = 0.8$, falls die $H_{1}$ gelten würde, tatsächlich ein Effekt von $\delta_{H_{1}} = 0.2$ vorliegen würde und Sie eine größere Stichprobengröße als die von Ihnen berechnete erheben würden?
  
  Lösung
  
  Die Power wäre in diesem Fall größer als 0.8.
5. Wie hoch wäre die Power Ihres Tests im Vergleich zu $1 - \beta = 0.8$, falls die $H_{1}$ gelten würde, tatsächlich ein Effekt von $\delta_{H_{1}} = 0.2$ vorliegen würde und Sie eine kleinere Stichprobengröße als die von Ihnen berechnete erheben würden?
  
  Lösung
  
  Die Power wäre in diesem Fall kleiner als 0.8.