Übungsblatt 13

False Discovery Rate und Annahmen statistischer Verfahren

  1. Sie betrachten eine Reihe von unabhängigen statistischen Hypothesentests, die alle ein Signifikanzniveau von \(\alpha = 0.005\) und eine Power von \(1 - \beta = 0.8\) aufweisen. Die Basisrate sei \(\rho = 0.5\).

    1. Was bedeutet eine Basisrate von \(\rho = 0.5\) inhaltlich?

      Dass 50% der überprüften Nullhypothesen wahr sind (bei \(\rho = 0.6\) wären dementsprechend 60% der Nullhypothesen wahr).

    2. Berechnen und interpretieren Sie die FDR.

      \[FDR = \frac{\alpha \cdot \rho}{\alpha \cdot \rho + (1 - \beta) \cdot (1 - \rho)} = \frac{0.005 \cdot 0.5}{0.005 \cdot 0.5 + 0.8 \cdot (1 - 0.5)} \approx 0.006\]

      Im Durchschnitt wären 0.6% der signifikanten Ergebnisse falsch.

    3. Wie würde sich die FDR bei gleichem Signifikanzniveau und gleicher Power verändern, wenn die Basisrate größer wäre?

      Sie würde größer werden.

    4. Wie würde sich die FDR bei gleichem Signifikanzniveau und gleicher Power verändern, wenn die Basisrate kleiner wäre?

      Sie würde kleiner werden.

    5. Wie würde sich die FDR bei gleichem Signifikanzniveau und gleicher Basisrate verändern, wenn die Power der Tests größer wäre?

      Sie würde kleiner werden.

    6. Wie würde sich die FDR bei gleicher Power und gleicher Basisrate verändern, wenn das Signifikanzniveau der Tests kleiner wäre?

      Sie würde kleiner werden.

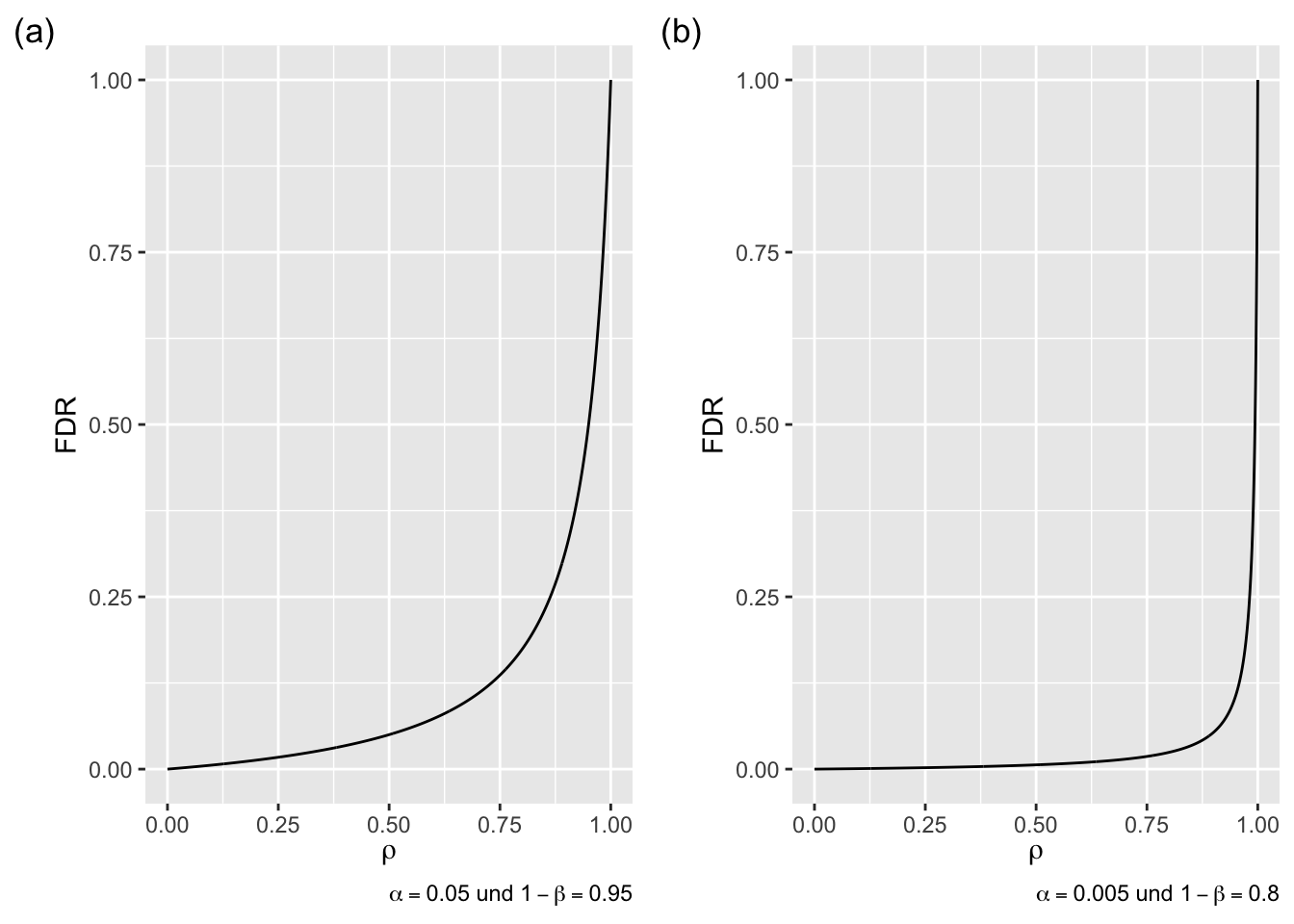
  2. In den folgenden Plots ist für zwei verschiedene Kombinationen von Signifikanzniveau und Power die FDR in Abhängigkeit von der Basisrate dargestellt:

    1. Geben Sie für beide Plots jeweils die Gleichung der Funktion an, die hier graphisch veranschaulicht ist.

      Allgemein (siehe Vorlesung Folie 21):

      \[FDR(\rho) = \frac{\alpha \cdot \rho}{\alpha \cdot \rho + (1 - \beta) \cdot (1 - \rho)} = \frac{\alpha}{\alpha + (1 - \beta) \cdot \left( \frac{1}{\rho} - 1 \right)}\]

      Für \(\alpha = 0.05\) und \(1 - \beta = 0.95\) ergibt sich:

      \[FDR(\rho) = \frac{0.05}{0.05 + 0.95 \cdot \left( \frac{1}{\rho} - 1 \right)} = \frac{0.05}{0.05 + \frac{0.95}{\rho} - 0.95} = \frac{0.05}{\frac{0.95}{\rho} - 0.9}\]

      Für \(\alpha = 0.005\) und \(1 - \beta = 0.8\):

      \[FDR(\rho) = \frac{0.005}{0.005 + 0.8 \cdot \left( \frac{1}{\rho} - 1 \right)} = \frac{0.005}{0.005 + \frac{0.8}{\rho} - 0.8} = \frac{0.005}{\frac{0.8}{\rho} - 0.795}\]

    2. Erläutern Sie, warum es sinnvoll sein könnte, statt einem Signifikanzniveau von \(\alpha = 0.05\) und einer Power von \(1 - \beta = 0.95\) ein Signifikanzniveau von \(\alpha = 0.005\) und eine Power von \(1 - \beta = 0.8\) vorauszusetzen.

      Da die FDR in diesem Fall weniger stark von der Basisrate abhängen würde. Auch für eine sehr ungünstige Basisrate von z.B. \(\rho = 0.9\) wäre die FDR immer noch sehr gering. Da wir die Basisrate weder bestimmen noch direkt kontrollieren können, ist eine geringe Abhängigkeit der FDR von dieser wünschenswert.

    3. Was könnte eine sinnvolle auf der Basis der Plots berechnete Maßzahl zur Beurteilung von beliebigen Kombinationen von Signifikanzniveau und Power sein?

      Man könnte die Fläche unter der Funktion als Maßzahl verwenden. Diese ließe sich für die beiden oben dargestellten Plots durch Integration der Funktionen aus Teilaufgabe a berechnen. Kleinere Werten würden für eine weniger starke Abhängigkeit der FDR von der Basisrate sprechen und wären somit zu bevorzugen.

  3. Berechnen Sie die kleinstmögliche FDR

    1. bei einer Basisrate von \(\rho = 0.3\) und einem Signifikanzniveau von \(\alpha = 0.05\)

      \[FDR = \frac{\alpha \cdot \rho}{\alpha \cdot \rho + 1 - \rho} = \frac{0.05 \cdot 0.3}{0.05 \cdot 0.3 + 1 - 0.3} = 0.02\]

    2. bei einer Basisrate von \(\rho = 0.8\) und einem Signifikanzniveau von \(\alpha = 0.05\)

      \[FDR = \frac{\alpha \cdot \rho}{\alpha \cdot \rho + 1 - \rho} = \frac{0.05 \cdot 0.8}{0.05 \cdot 0.8 + 1 - 0.8} = 0.17\]

    3. bei einer Basisrate von \(\rho = 0.3\) und einem Signifikanzniveau von \(\alpha = 0.005\)

      \[FDR = \frac{\alpha \cdot \rho}{\alpha \cdot \rho + 1 - \rho} = \frac{0.005 \cdot 0.3}{0.005 \cdot 0.3 + 1 - 0.3} = 0.002\]

    4. bei einer Basisrate von \(\rho = 0.8\) und einem Signifikanzniveau von \(\alpha = 0.005\)

      \[FDR = \frac{\alpha \cdot \rho}{\alpha \cdot \rho + 1 - \rho} = \frac{0.005 \cdot 0.8}{0.005 \cdot 0.8 + 1 - 0.8} = 0.02\]

  4. Berechnen Sie die Basisrate, welche die in Nosek et al. (2015) geschätzte FDR von 0.63 bei einem Signifikanzniveau von \(\alpha = 0.05\) und einer Power von \(1 - \beta = 0.35\) implizieren würde. Welche Gründe für eine hohe FDR könnte es außer Signifikanzniveau, Power und Basisrate noch geben?

    Auflösen von

    \[FDR = \frac{\alpha \cdot \rho}{\alpha \cdot \rho + (1 - \beta) \cdot (1 - \rho)}\]

    nach \(\rho\):

    \[FDR \cdot \left( \alpha \cdot \rho + (1 - \beta) \cdot (1 - \rho) \right) = \alpha \cdot \rho\]

    \[FDR \cdot \alpha \cdot \rho + FDR \cdot (1 - \beta) - FDR \cdot (1 - \beta) \cdot \rho - \alpha \cdot \rho = 0\]

    \[\left( FDR \cdot \alpha - FDR \cdot (1 - \beta) - \alpha \right) \cdot \rho = - FDR \cdot (1 - \beta)\]

    \[\rho = - \frac{FDR \cdot (1 - \beta)}{FDR \cdot \alpha - FDR \cdot (1 - \beta) - \alpha}\]

    Einsetzen von \(FDR = 0.63\), \(\alpha = 0.05\) und \(1 - \beta = 0.35\):

    \[\rho = - \frac{0.63 \cdot 0.35}{0.63 \cdot 0.05 - 0.63 \cdot 0.35 - 0.05} = 0.92\]

    Weitere mögliche Gründe für eine hohe FDR wären z.B.:

    • Verletzungen der Annahmen der statistischen Hypothesentests

    • Fehlende Repräsentativität der Stichproben

    • Fehler bei Datenerhebung oder -auswertung

    • Datenmanipulation

    • etc.

  1. Sie vermuten, dass sich zwei Populationen in ihrer durchschnittlichen Abiturnote unterscheiden. Sie ziehen jeweils eine einfache Zufallsstichprobe aus den beiden Populationen.

    1. Laden Sie den Datensatz herunter und führen Sie das entsprechende inferenzstatistische Verfahren in R unter der Annahme durch, dass das Histogramm der Abiturnoten in beiden Populationen durch die Dichtefunktion einer Normalverteilung approximiert werden kann und dass die empirische Varianz der Abiturnoten in beiden Populationen gleich ist. Falls Sie ein Konfidenzintervall berechnen, wählen Sie ein Konfidenzniveau von 0.95. Falls Sie einen Hypothesentest durchführen, wählen Sie ein Signifikanzniveau von 0.005. Interpretieren Sie das Ergebnis.

      Da wir uns für die Hypothesen \[ \begin{align*} H_0: \mu_{Gruppe1}-\mu_{Gruppe2}=0 \\ H_1: \mu_{Gruppe1}-\mu_{Gruppe2}\neq 0 \end{align*} \]

      interessieren und zwei unabhängige Stichproben gezogen haben, wählen wir einen ungerichteten Zweistichproben t-Test für unabhängige Stichproben.

      daten <- read.csv2('daten_abi.csv')
daten_1 <- daten[daten$gruppe == "Gruppe1", ]
daten_2 <- daten[daten$gruppe == "Gruppe2", ]

t.test(daten_1$abinote, daten_2$abinote, mu = 0,
       alternative = 'two.sided', paired = FALSE, var.equal = TRUE)
      
    Two Sample t-test

data:  daten_1$abinote and daten_2$abinote
t = -5.4647, df = 1998, p-value = 5.218e-08
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -0.2634884 -0.1243141
sample estimates:
mean of x mean of y 
 2.521820  2.715722

      Der p-Wert ist 0.00000005218 und somit kleiner als das Signifikanzniveau \(\alpha=0.005\). Wir entscheiden uns daher für die \(H_1\) und somit dafür, dass sich die beiden Populationen in ihrer durchschnittlichen Abiturnote unterscheiden.

    2. Berechnen Sie die empirische Varianz der Abiturnoten in beiden Stichproben und erstellen Sie ein Histogramm der Abiturnoten in beiden Stichproben. Sprechen die Stichprobendaten für eine Verletzung der Annahmen?

      var(daten_1$abinote)
      [1] 0.7632201
      var(daten_2$abinote)
      [1] 0.4958087
      hist(daten_1$abinote)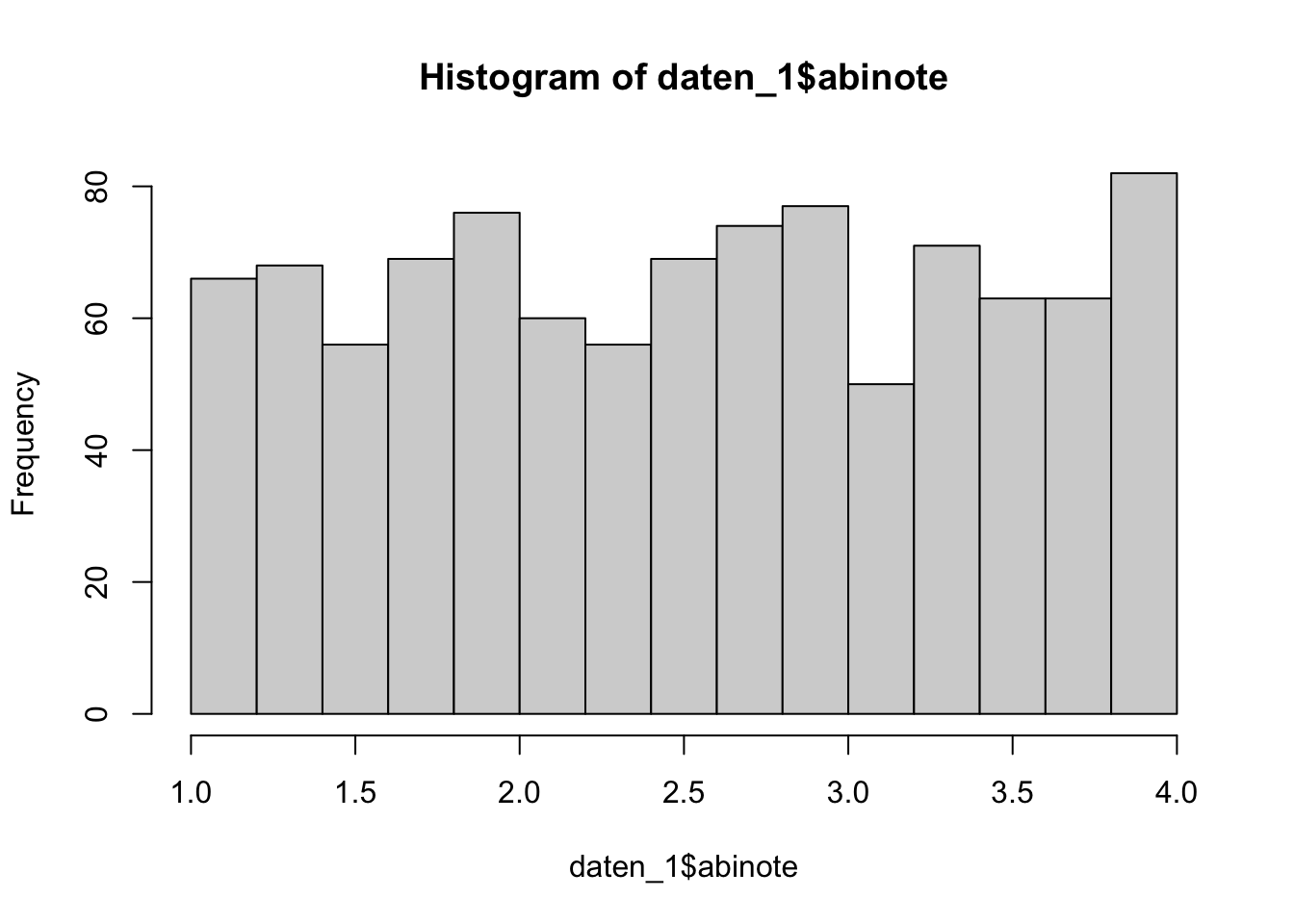

      hist(daten_2$abinote)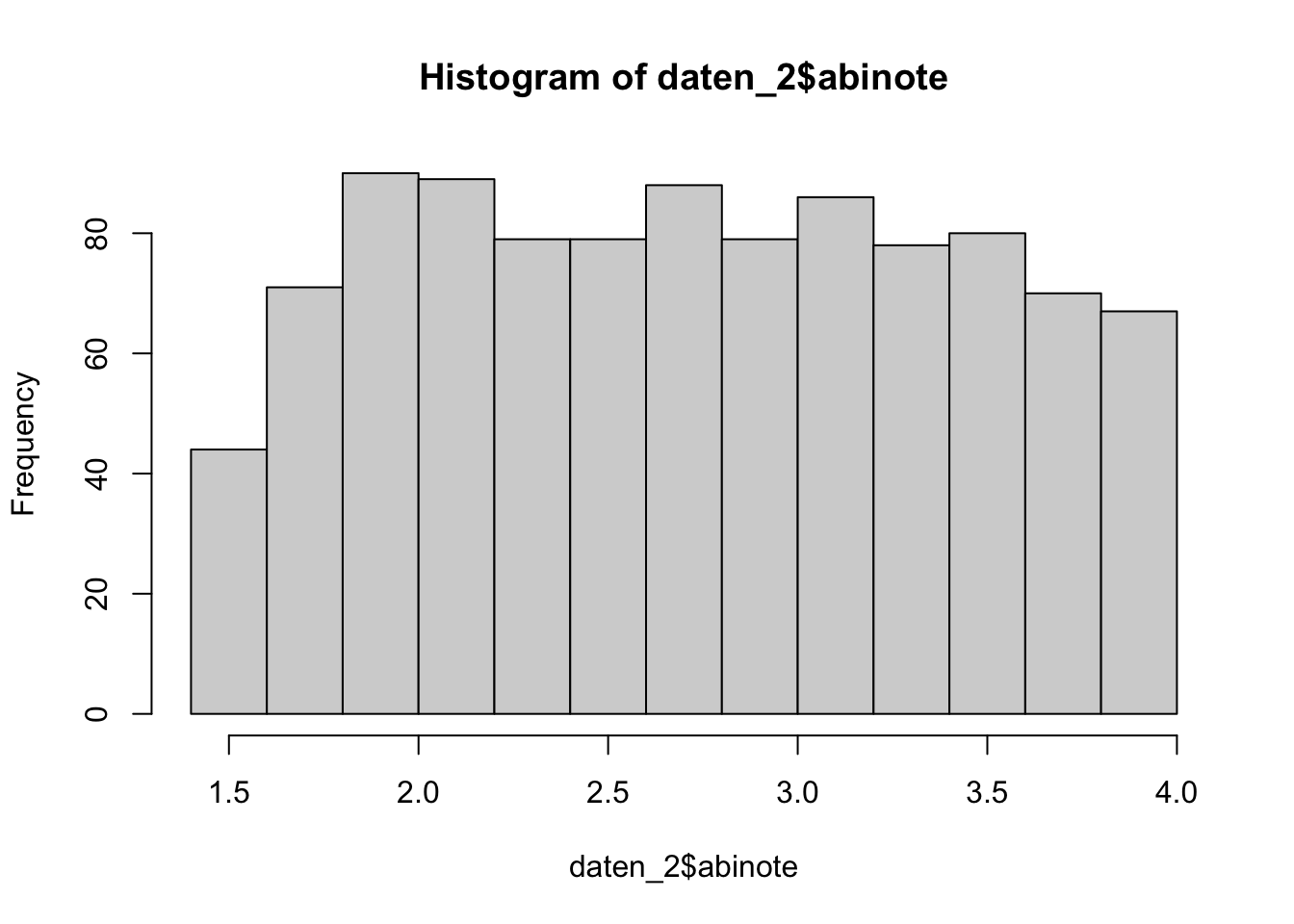

      Die empirischen Varianzen sind in den beiden Stichproben nicht gleich groß. Wir können jedoch nicht sagen, ob sie sich so stark unterscheiden, dass die Annahme gleicher Varianzen in der Population unplausibel erscheint. Die Histogramme könnten zumindest in der Stichprobe nicht durch die Dichtefunktion einer Normalverteilung approximiert werden. Insgesamt sprechen die Stichprobendaten eher für eine Verletzung der Annahmen, vor allem da die Stichprobe sehr groß ist. Dies ist jedoch eine sehr subjektive Einschätzung.

    3. Welche Konsequenzen hätte es für das von Ihnen gewählte Verfahren, falls alle Annahmen verletzt wären?

      In diesem Fall hätte der von uns verwendete Hypothesentest nicht das gewünschte Signifikanzniveau \(\alpha=0.005\). Da die Stichprobe aber groß ist, können wir davon ausgehen, dass das Signifikanzniveau in diesem Fall trotzdem approximativ gleich \(\alpha=0.005\) ist.