Übungsblatt 03

DESKRIPTIVE STATISTIK II: Korrelation

  1. Welche Eigenschaften sollte eine Maßzahl haben, die einen linearen Zusammenhang zwischen zwei Variablen beschreibt? Geben Sie an, welche dieser Eigenschaften Kovarianz und Korrelation jeweils aufweisen.

    Eine sinnvolle Maßzahl für den Zusammenhang zweier Variablen sollte

    • die Richtung des Zusammenhangs abbilden.
    • die Stärke des Zusammenhangs abbilden.
    • Unabhängig von der Einheit der Variablen sein.

    Die Korrelation besitzt alle diese Eigenschaften, die Kovarianz lediglich die erste.

  2. Ihnen liegen die folgenden Daten vor:

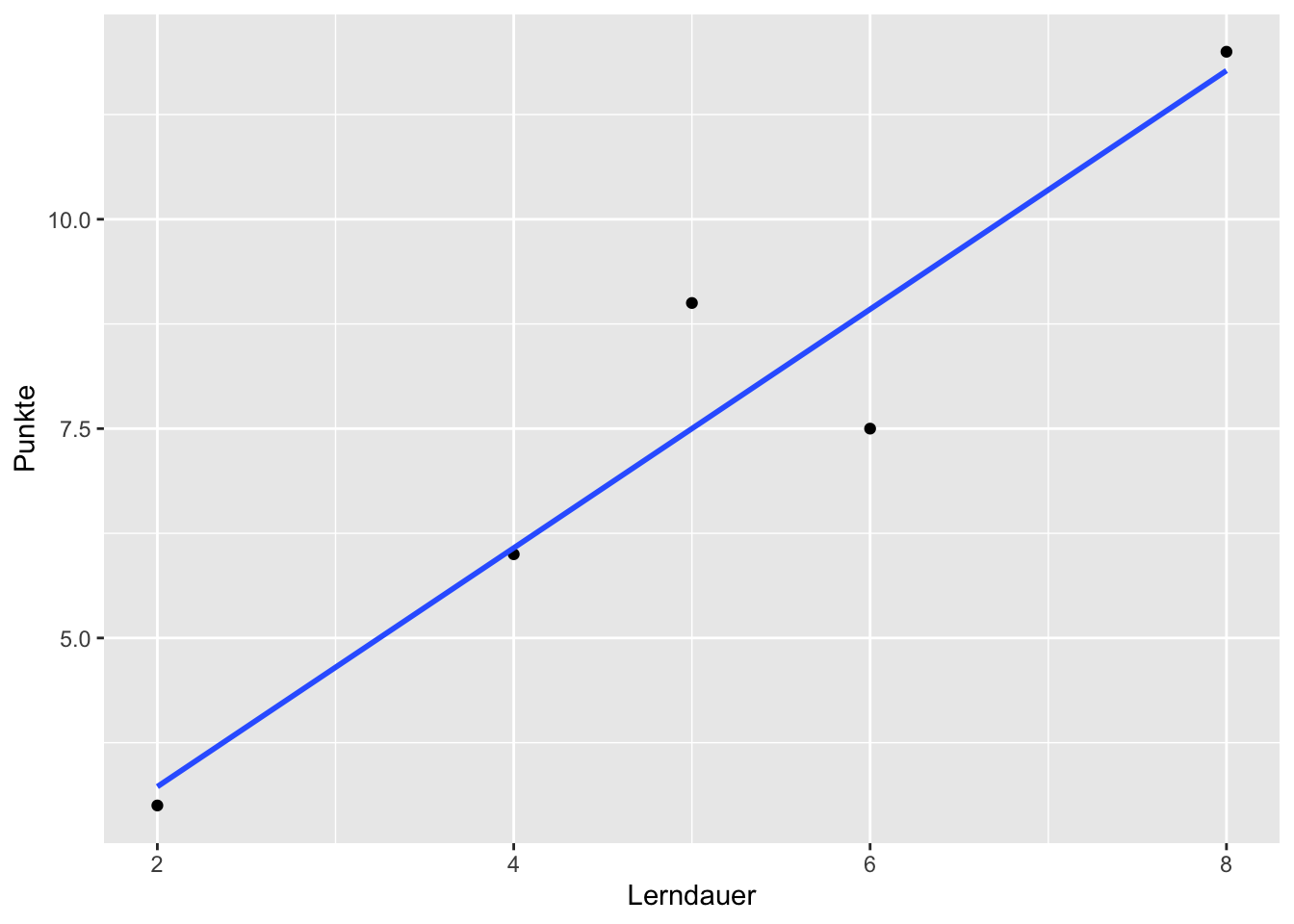
    Lerndauer in Stunden Punkte in der Klausur
    Schüler 1 2 3
    Schüler 2 4 6
    Schüler 3 6 7.5
    Schüler 4 5 9
    Schüler 5 8 12

    1. Zeichnen Sie basierend auf diesen Daten ein Streudiagramm.

      Streudiagramm von Lerndauer und Punkten in der Klausur

    2. Welche Richtung hat der Zusammenhang? Drücken Sie diesen in Worten aus.

      Es liegt ein gleichgerichteter Zusammenhang vor. Je länger die Schüler lernen, desto mehr Punkte erreichen sie im Durchschnitt in der Klausur.

    3. Welches Vorzeichen würden Sie für die Kovarianz erwarten?

      Da die Kovarianz die Richtung des Zusammenhangs durch ihr Vorzeichen ausdrückt, würde man in diesem Fall ein positives Vorzeichen erwarten.

    4. Berechnen Sie die Kovarianz und interpretieren Sie diese.

      \[\bar{x} = 5\]

      \[\bar{y} = 7.5\]

      \[ \begin{align*} {cov}_{emp}(x,\ y) &= \frac{1}{n}\sum_{i = 1}^{n}\left( x_{i} - \bar{x} \right)\left( y_{i} - \bar{y} \right) \\ &= \frac{1}{5}\sum_{i = 1}^{5}\left( x_{i} - 5 \right)\left( y_{i} - 7.5 \right) \\ &= \frac{1}{5}\left\lbrack \left( x_{1} - 5 \right)\left( y_{1} - 7.5 \right) + \ldots + \left( x_{5} - 5 \right)\left( y_{5} - 7.5 \right) \right\rbrack \\ &= \frac{1}{5}\left\lbrack (2 - 5)(3 - 7.5) + \ldots + (8 - 5)(12 - 7.5) \right\rbrack = 5.7 \end{align*} \] Da an der Kovarianz lediglich die Richtung des Zusammenhangs abgelesen werden kann, können wir nur sagen, dass ein gleichgerichteter Zusammenhang der Variablen Lerndauer und Klausurpunkte vorliegt.

    5. BONUS: Berechnen Sie die Steigung der bestmöglichen Geraden durch die Messwertpaare und zeichnen Sie diese in das Streudiagramm aus Teilaufgabe a) ein (Hinweis: der Achsenabschnitt ist 0.375).

      \[ \begin{align*} &{cov}_{emp}(x,\ y) = \ b \times s_{emp\ x}^{2} \\ &b = \frac{{cov}_{emp}(x,y)}{s_{emp\ x}^{2}} \\ &s_{emp\ x}^{2} = 4 \\ &b = \frac{5.7}{4} = 1.425 \end{align*} \]

    6. Z-standardisieren Sie beide Variablen.

      zx zy
      Schüler 1 -1.5 -1.5
      Schüler 2 -0.5 -0.5
      Schüler 3 0.5 0
      Schüler 4 0 0.5
      Schüler 5 1.5 1.5

    7. Berechnen Sie die Korrelation und interpretieren Sie diese.

      \[ \begin{align*} r_{xy} &= \frac{1}{n}\sum_{i = 1}^{n}{z_{x_{i}}\cdot z_{y_{i}}} \\ &= \frac{1}{5}\sum_{i = 1}^{5}{z_{x_{i}}\cdot z_{y_{i}}} \\ &= \frac{1}{5}\left\lbrack z_{x_{1}}\cdot z_{y_{1}} + \ldots + z_{x_{5}}\cdot z_{y_{5}} \right\rbrack \\ &= \frac{1}{5}\left\lbrack ( - 1.5)\cdot( - 1.5) + \ldots + 1.5\cdot 1.5 \right\rbrack = 0.95 \end{align*} \]

      Es liegt ein starker gleichgerichteter Zusammenhang der Variablen Lerndauer und Klausurpunkte vor.

    8. Geben Sie die Steigung der bestmöglichen Geraden durch die z-standardisierten Messwertpaare aus Teilaufgabe f) an.

      \[b_{z} = r_{xy} = 0.95\]

  3. Sie lesen in einer Tageszeitung folgende Schlagzeile:

    „Medizinische Überversorgung kostet Menschenleben. Menschen, die häufiger zum Arzt gehen haben deutlich niedrigere Lebenserwartung!”

    Wie könnte man sich den in der Schlagzeile beschriebenen Zusammenhang alternativ erklären und welcher Fehler ist den Autoren des Artikels bei der Interpretation unterlaufen?

    Alternativerklärung: Personen mit ernsten gesundheitlichen Problemen gehen deutlich häufiger zum Arzt als Gesunde. Außerdem haben sie aufgrund ihrer Erkrankung eine niedrigere Lebenserwartung als Gesunde. Die Autoren des Zeitungsartikels interpretieren einen korrelativen Zusammenhang als läge ein kausaler Zusammenhang vor.

    Bei der Korrelation \(r_{xy}\) handelt es sich um ein deskriptivstatistisches Maß zur Beschreibung linearer Zusammenhänge zweier Variablen. Der Wert \(r_{xy}\) sagt nichts darüber aus, welche Variable von welcher beeinflusst wird oder ob beide Variablen von einer Drittvariable beeinflusst werden.

    Kausale Schlussfolgerungen können grundsätzlich nur gezogen werden, wenn ein Experiment durchgeführt wurde.

  4. Warum sollte einer Korrelationsanalyse immer eine grafische Begutachtung der Daten vorausgehen?

    Die Korrelation stellt ein Maß für einen linearen Zusammenhang dar. Im Streudiagramm muss daher zuerst festgestellt werden, ob überhaupt ein linearer Zusammenhang vorliegt. Liegt ein nonlinearer Zusammenhang vor, ist die Korrelation nicht geeignet, den Zusammenhang zu beschreiben. Zum Beispiel kann für einen quadratischen Zusammenhang eine Korrelation von 0 resultieren (siehe Vorlesung). Außerdem muss überprüft werden, ob Ausreißer vorliegen, die die Korrelation verzerren könnten.

  1. Bitte laden Sie für die folgenden Aufgaben den Datensatz herunter. Dieser Datensatz enthält (fiktive) Daten zur körperlichen Leistungsfähigkeit von Schülern aus zwei verschiedenen Schulklassen (Klasse 1 und Klasse 2), unter anderem die Variablen „Anzahl Liegestütz” und „Sprungweite in cm”. Lesen Sie den Datensatz über den Befehl read.csv2() in R ein:

    Daten <- read.csv2("Sportdaten.csv")

    1. Erstellen Sie für beide Klassen jeweils ein Streudiagramm mit der Variable „liegestuetz” auf der x-Achse und der Variable „sprungweite_cm” auf der y-Achse.

      Für die Erstellung der Streudiagramme ist es hilfreich, wenn Sie den Datensatz zunächst nach Klassen aufteilen und jede Klasse als eigenen data.frame in einem Objekt speichern:

      Daten1 <- Daten[Daten$Klasse == 1, ]
Daten2 <- Daten[Daten$Klasse == 2, ]

      Mit dem Befehl plot() können Sie dann das Streudiagramm für die Klasse 1 und dasjenige für die Klasse 2 erstellen. Als erstes und zweites Argument geben Sie dabei die beiden Variablen an, die Sie in dem Streudiagramm darstellen möchten. Mit den zusätzlichen Argumenten xlab bzw. ylab können Sie Beschriftungen der x- und y-Achse angeben. Verwenden Sie zudem das Argument ylim = c(0, 400), um für beide Streudiagramme die y- Achse auf das Intervall von 0 bis 400 zu skalieren.

      Zum Beispiel:

      plot(Variable1, Variable2, 
     xlab = "Anzahl Liegestuetz", 
     ylab = "Sprungweite in cm", 
     ylim = c(0, 400))

      Können Sie in beiden Klassen von einem linearen Zusammenhang der Variablen ausgehen?

      Wenn ja, in welcher Klasse würden Sie von einem stärkeren Zusammenhang zwischen den beiden Variablen sprechen? Begründen Sie.

      ## Streudiagramm Klasse 1
plot(Daten1$liegestuetz, Daten1$sprungweite_cm,
     main = "Klasse 1",
     xlab = 'Anzahl Liegestuetz',
     ylab = 'Sprungweite in cm',
     ylim = c(0, 400))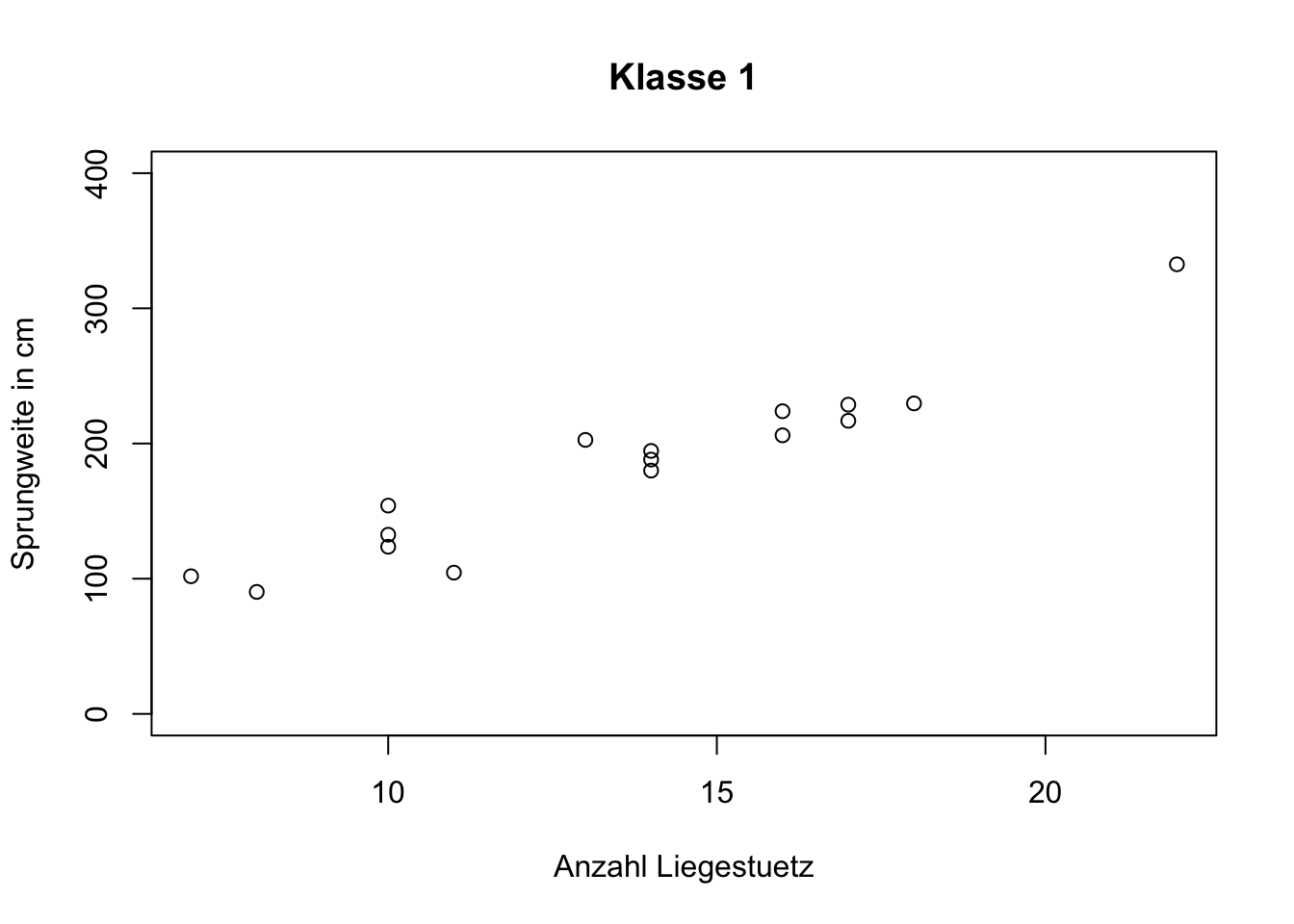

      ## Streudiagramm Klasse 2
plot(Daten2$liegestuetz, Daten2$sprungweite_cm,
     main = "Klasse 2",
     xlab = 'Anzahl Liegestuetz',
     ylab = 'Sprungweite in cm',
     ylim = c(0, 400))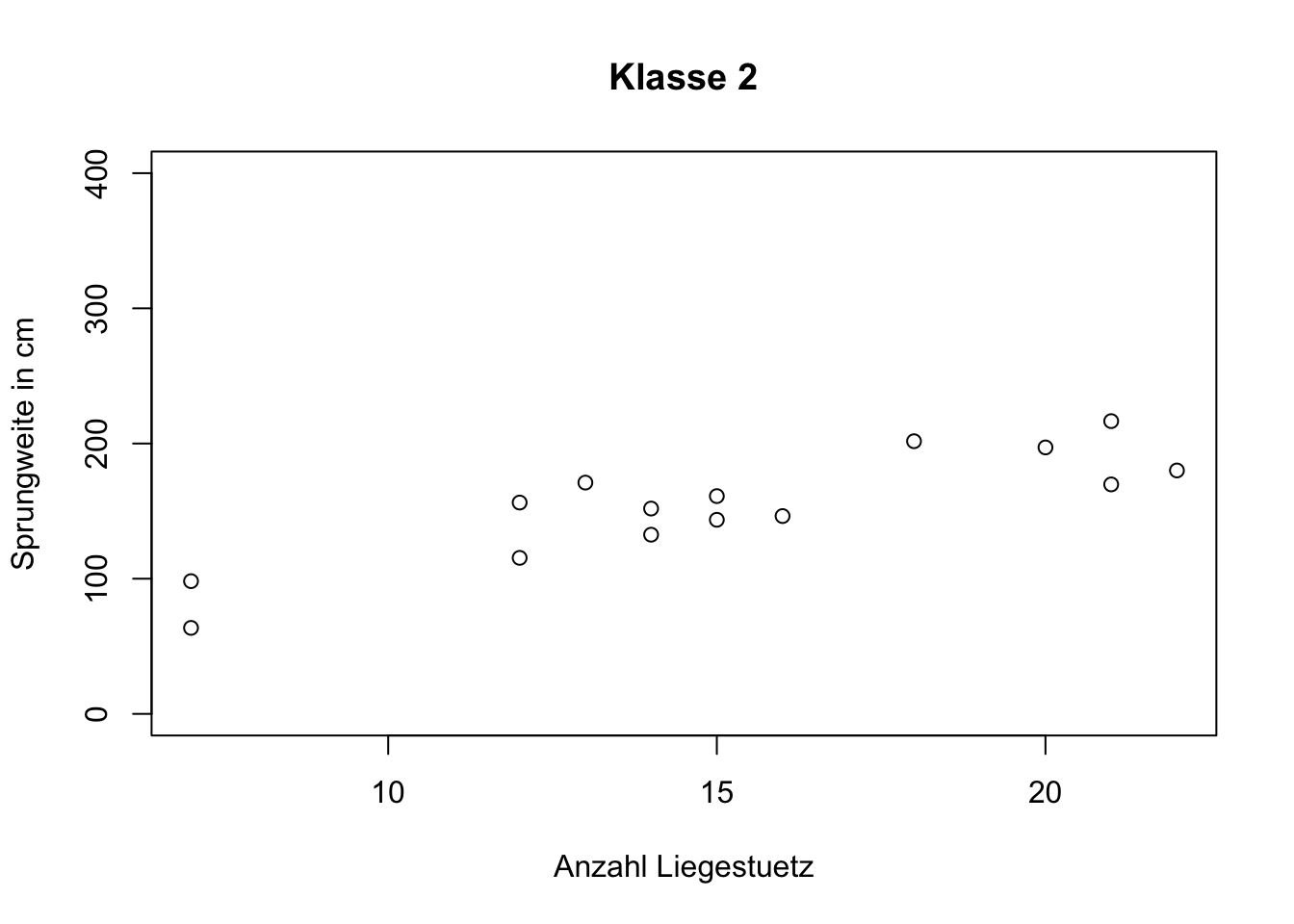

      ## Bemerkung: Im Allgemeinen müssen Sie das ylim Argument nicht
## verwenden. Wir benötigen es in unserem Fall nur, damit beide
## Streudiagramme die gleiche Skalierung aufweisen und wir die
## Steigungen vergleichen können.

      In beiden Fällen liegt ein linearer gleichgerichteter Zusammenhang zwischen den Variablen vor. Der Zusammenhang erscheint in Klasse 1 aufgrund der stärkeren Steigung bei ähnlicher Streuung der Messwerte um die Gerade etwas stärker.

    2. Berechnen Sie sowohl für Klasse 1 als auch für Klasse 2 die Kovarianz zwischen den Variablen „liegestuetz” und „sprungweite_cm” mithilfe des Befehls cov().

      ## Kovarianz Klasse 1
cov(Daten1$liegestuetz, Daten1$sprungweite_cm)
      [1] 242.5221
      ## Kovarianz Klasse 2
cov(Daten2$liegestuetz, Daten2$sprungweite_cm)
      [1] 162.2601

    3. Berechnen Sie sowohl für Klasse 1 als auch für Klasse 2 die Korrelation zwischen den Variablen „liegestuetz” und „sprungweite_cm” mithilfe des Befehls cor(). Interpretieren Sie diese. In welcher Klasse liegt ein stärkerer Zusammenhang der Variablen vor?

      ## Korrelation Klasse 1
cor(Daten1$liegestuetz, Daten1$sprungweite_cm)
      [1] 0.95664
      ## Korrelation Klasse 2
cor(Daten2$liegestuetz, Daten2$sprungweite_cm)
      [1] 0.8589913

      In beiden Klassen liegt ein starker gleichgerichteter Zusammenhang zwischen den Variablen „Anzahl Liegestütz” und „Sprungweite in cm” vor. Der Zusammenhang ist in Klasse 1 stärker.

    4. Rechnen Sie für die Klasse 1 die Variable „sprungweite_cm” von cm in km um und fügen Sie diese als Variable „sprungweite_km” zu dem Datensatz der Klasse 1 hinzu. Berechnen Sie nun in Klasse 1 die Kovarianz und die Korrelation zwischen den Variablen „liegestuetz” und „sprungweite_km”. Was fällt Ihnen auf?

      ## Sprungsweite in Klasse 1 in km umrechnen und zum Datensatz hinzufügen
Daten1$sprungweite_km <- Daten1$sprungweite_cm / 100000

## Nochmal Kovarianz und Korrelation
cov(Daten1$liegestuetz, Daten1$sprungweite_km)
      [1] 0.002425221
      cor(Daten1$liegestuetz, Daten1$sprungweite_km)
      [1] 0.95664

      Während sich die Kovarianz durch den Einheitswechsel deutlich ändert, bleibt die Korrelation gleich. An diesem Beispiel zeigen sich Einheitsabhängigkeit der Kovarianz und Einheitsunabhängigkeit der Korrelation.

  2. BONUS: Zeigen Sie, dass für z-standardisierte Messwerte stets

    \[\bar{z} = \frac{1}{n}\sum_{i = 1}^{n}z_{i} = 0\]

    gilt.

    \[ \begin{align*} \bar{z} &= \frac{1}{n}\sum_{i=1}^n z_i \\ &= \frac{1}{n}\sum_{i=1}^n \left( \frac{x_i - \bar{x}}{s_{emp}} \right) \\ &= \frac{1}{n \cdot s_{emp}} \sum_{i= 1}^n (x_i - \bar{x})\\ &= \frac{1}{n \cdot s_{emp}} \left(\sum_{i= 1}^n x_i - \sum_{i = 1}^n \bar{x} \right)\\ &= \frac{1}{n \cdot s_{emp}} \left(\sum_{i= 1}^n x_i - n \cdot \bar{x}\right)\\ &= \frac{1}{s_{emp}} \left(\frac{1}{n}\sum_{i= 1}^n x_i - \frac{n}{n} \cdot \bar{x}\right)\\ &= \frac{1}{s_{emp}} \left(\bar{x} - \bar{x}\right)\\ &= \frac{1}{s_{emp}} \cdot 0 = 0\\ \end{align*} \]