Übungsblatt 05

Wahrscheinlichkeitsdichtefunktion, Verteilungsfunktion, Erwartungswert, Varianz, z-Standardisierung von Zufallsvariablen und Binomialverteilung

  1. Was versteht man unter Inferenzstatistik? Denken Sie sich eine psychologische Fragestellung aus, zu deren Beantwortung Sie inferenzstatistische Methoden verwenden müssten. Welche Rolle spielt die Wahrscheinlichkeitstheorie in der Inferenzstatistik?

    Die Inferenzstatistik umfasst alle statistischen Verfahren, die es erlauben, trotz der
    Informationsunvollständigkeit der Stichprobendaten Aussagen über eine Population zu treffen.

    Beispiel: Wir wollen wissen, wie groß der Anteil der Personen in der Population der an Depression erkrankten Personen ist, bei dem unsere Psychotherapie zu einem Rückgang an Symptomen führt. Da wir nicht alle Depressiven mit unserer Therapie behandeln können, behandeln wir nur eine Stichprobe von Depressiven und schließen mithilfe inferenzstatistischer Verfahren auf die Population aller Depressiven.

    Um eine Stichprobe zu erhalten, ziehen wir Personen zufällig aus der Population. Die Wahrscheinlichkeitstheorie erlaubt es uns, diesen Zufallsprozess mathematisch zu beschreiben. Hieraus lassen sich dann die Methoden der Inferenzstatistik ableiten.

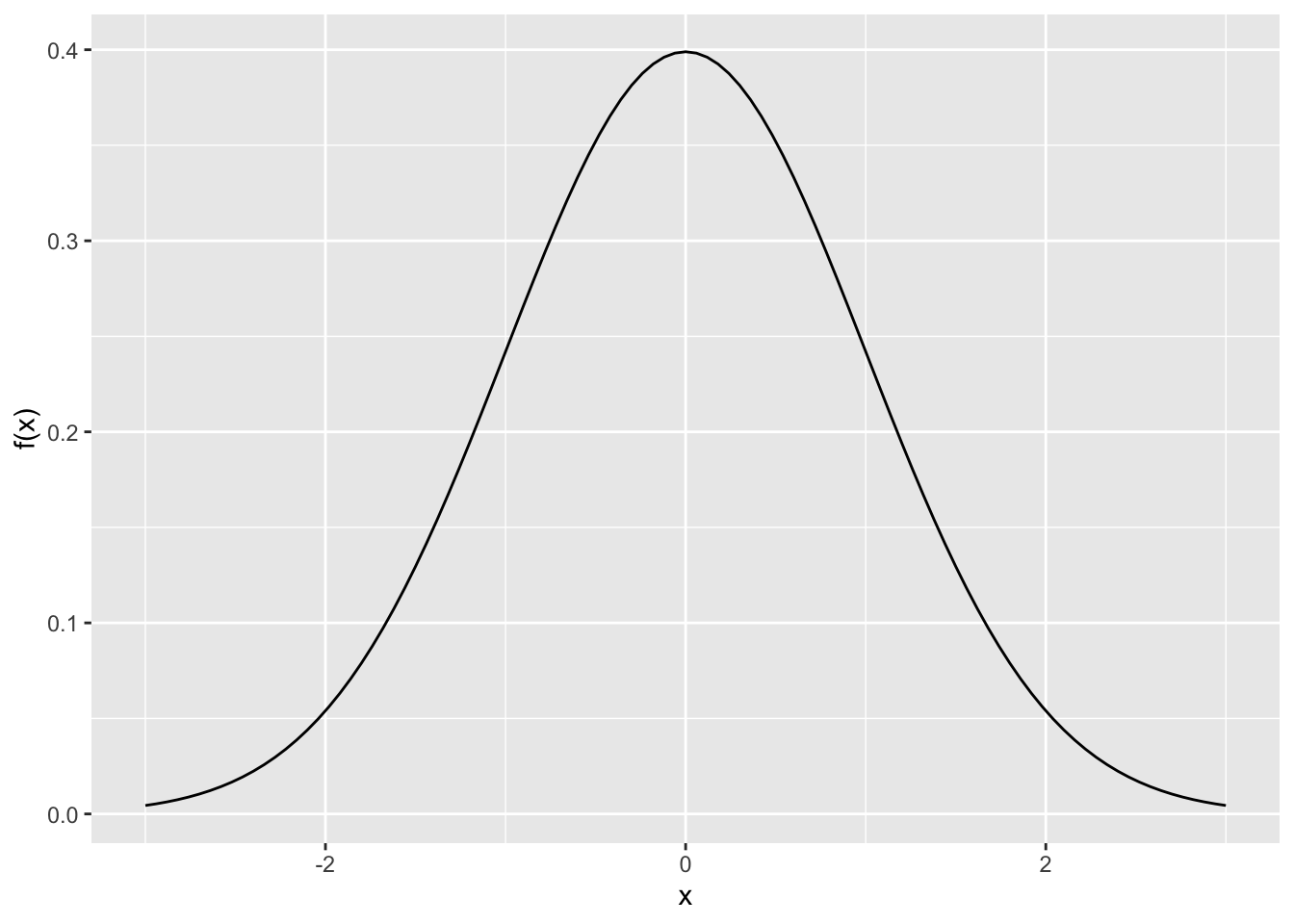
  2. Sei X eine stetige Zufallsvariable mit Träger \(T_{X}\mathbb{= R}\) und folgender Wahrscheinlichkeitsdichtefunktion:

    \(f(x) = \frac{1}{\sqrt{2\pi}}\exp\left( - \frac{x^{2}}{2} \right)\)

    x-Achse von -3 bis 3, y-Achse von 0.0 bis 0.4, Normalverteilung eingezeichnet mit Hochpunkt bei x = 0 und y = 0.4

    1. Schraffieren Sie jeweils die Fläche unter der Wahrscheinlichkeitsdichtefunktion, die Sie berechnen müssten, um die folgenden Wahrscheinlichkeiten zu bestimmen:

      1. \(P(X > 2) = P_{X}\left( \left\rbrack 2,\ \infty \right\lbrack \right)\)

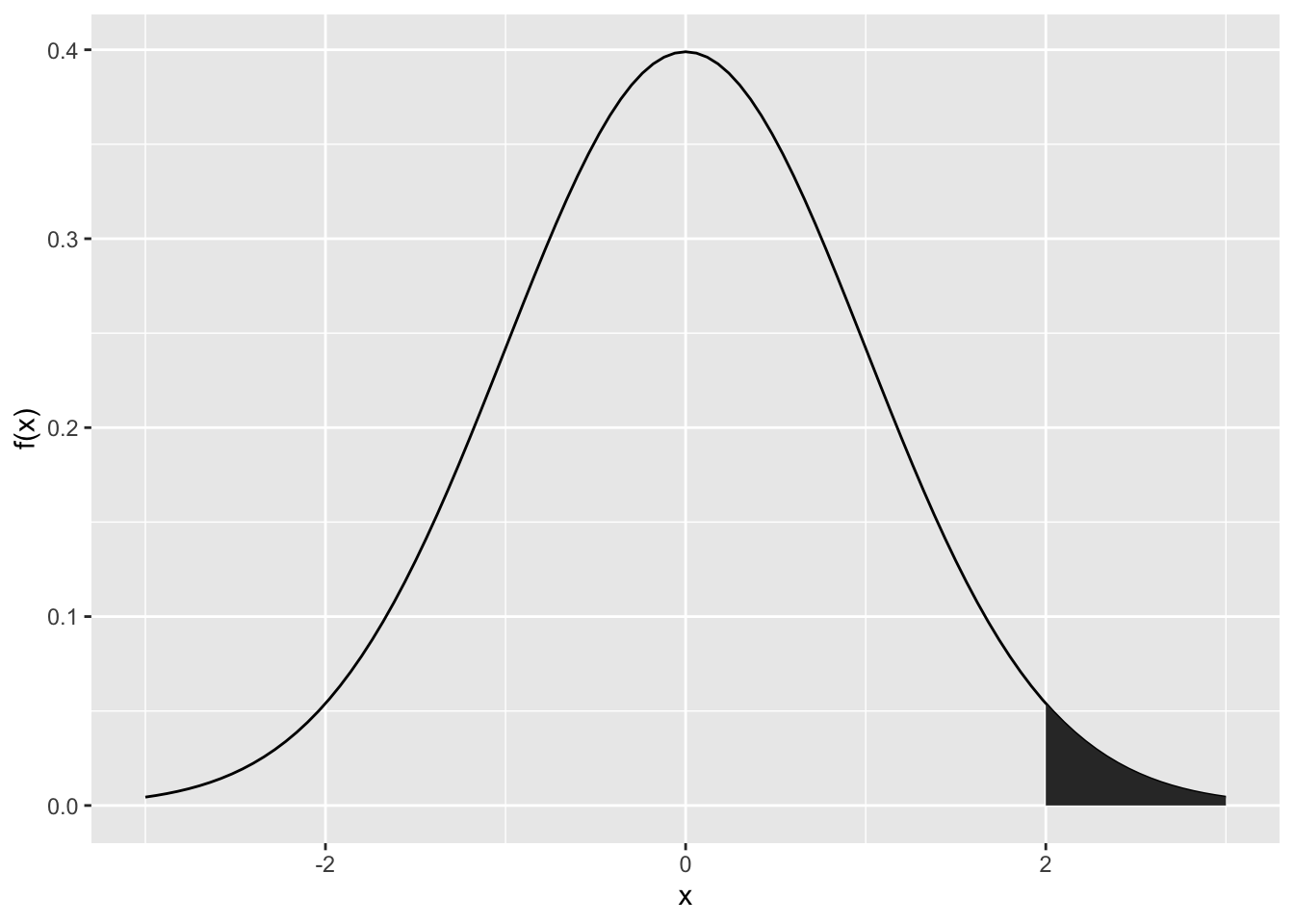
        x-Achse von -3 bis 3, y-Achse von 0.0 bis 0.4, Normalverteilung eingezeichnet mit Hochpunkt bei x = 0 und y = 0.4, Fläche unter der Kurve ab x = 2 schraffiert

      2. \(P(X \leq 0) = P_{X}\left( \left\rbrack - \infty,\ 0 \right\rbrack \right)\)

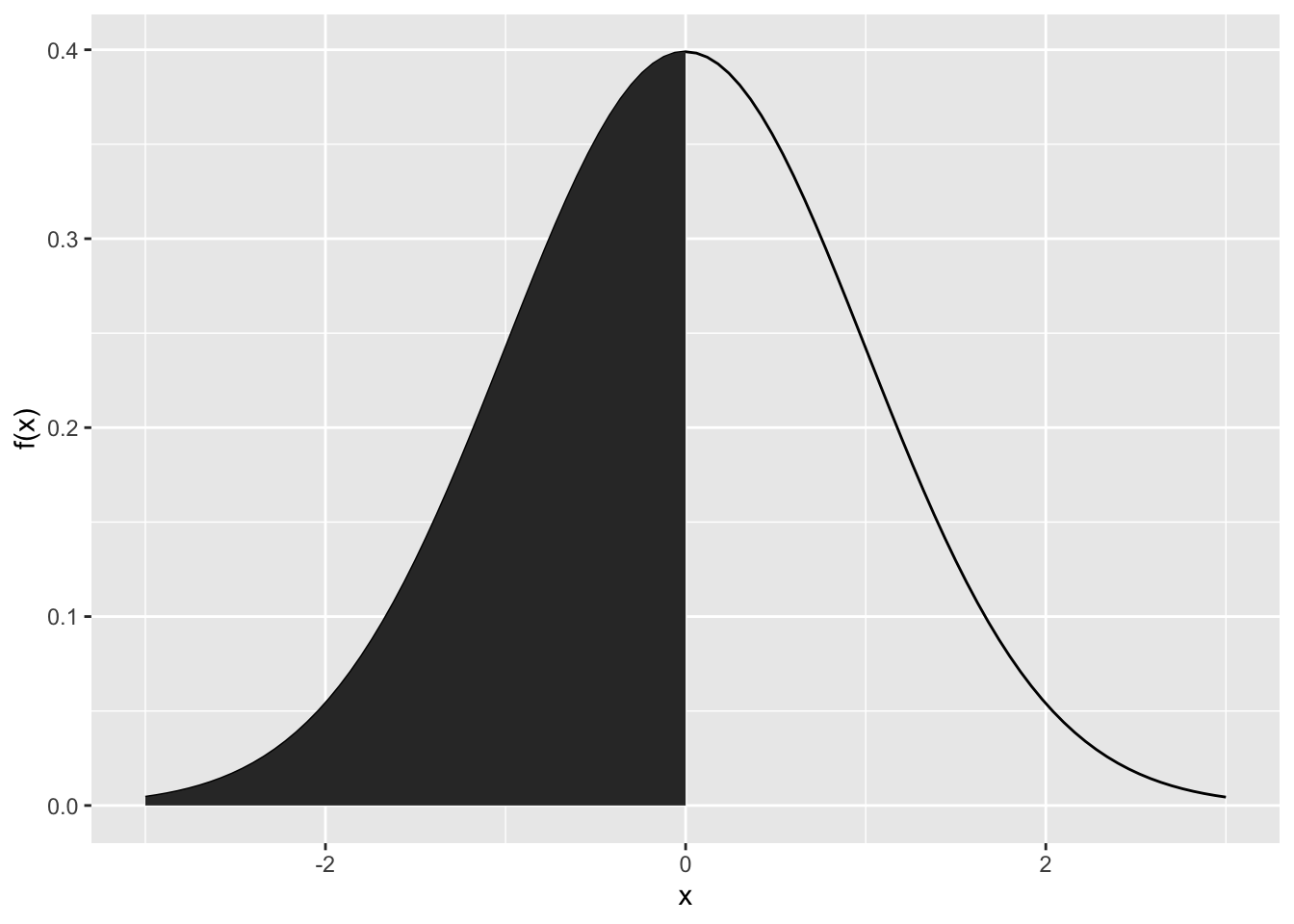
        x-Achse von -3 bis 3, y-Achse von 0.0 bis 0.4, Normalverteilung eingezeichnet mit Hochpunkt bei x = 0 und y = 0.4, Fläche unter der Kurve von x = -3 bis x = 0 schraffiert

      3. \(P( - 1 < X \leq 2) = P_{X}\left( \left\rbrack - 1,\ 2 \right\rbrack \right)\)

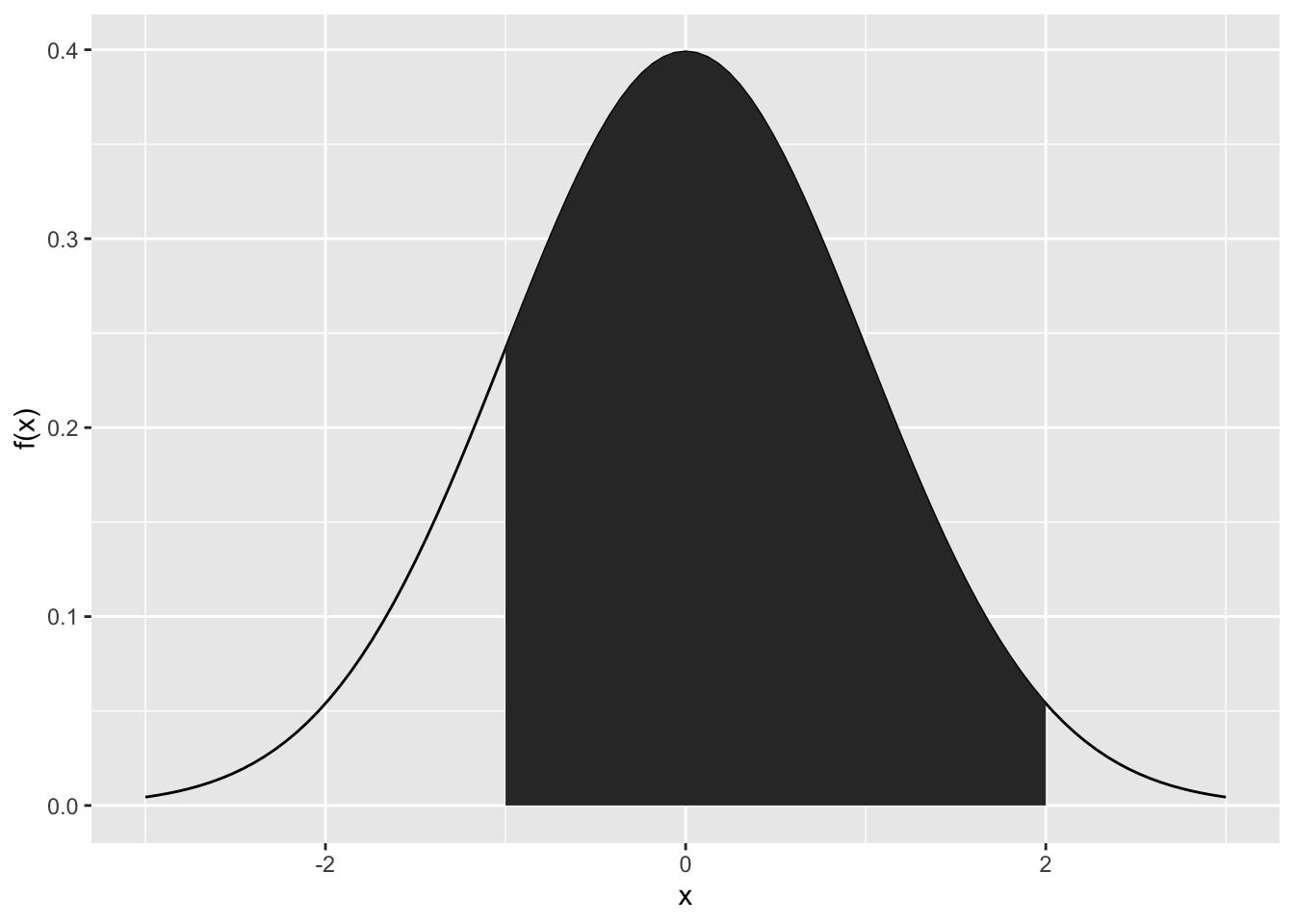
        x-Achse von -3 bis 3, y-Achse von 0.0 bis 0.4, Normalverteilung eingezeichnet mit Hochpunkt bei x = 0 und y = 0.4, Fläche unter der Kurve von x = -1 bis x = 2 schraffiert

      4. \(P\left( |X| \geq 2 \right) = P_{X}\left( \left\rbrack - \infty,\ - 2 \right\rbrack \cup \left\lbrack 2,\ \infty \right\lbrack \right)\)

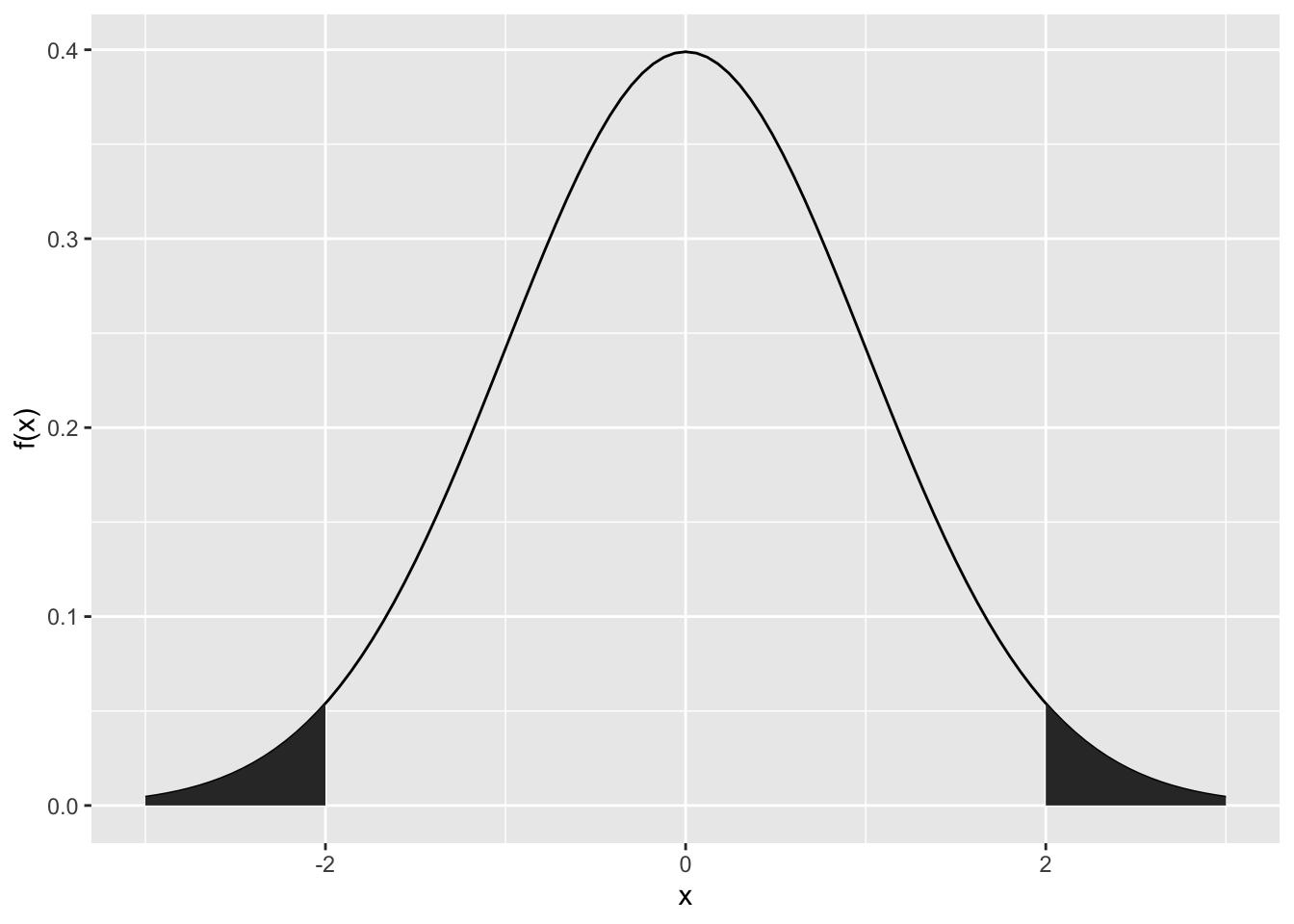
        x-Achse von -3 bis 3, y-Achse von 0.0 bis 0.4, Normalverteilung eingezeichnet mit Hochpunkt bei x = 0 und y = 0.4, Fläche unter der Kurve von x = -3 bis x = -2 und von x = 2 bis x = 3 schraffiert

    2. Sie kennen für einige Realisationen den Wert der Verteilungsfunktion von X:

      \[x\] -2 -1 0 1 2
      \[F(x)\] 0.02 0.16 0.5 0.84 0.98

      Berechnen Sie mithilfe dieser Werte die Wahrscheinlichkeiten aus Teilaufgabe a

      Hinweis: Für stetige Zufallsvariablen ist \(P(X < x) = P(X \leq x)\)

      1. \[P(X > 2) = 1 - P(X \leq 2) = 1 - F(2) = 1 - 0.98 = 0.02\]

      2. \[P(X \leq 0) = F(0) = 0.5\]

      3. \[P( - 1 < X \leq 2) = P(X \leq 2) - P(X \leq - 1) = F(2) - F( - 1) = 0.98 - 0.16 = 0.82\]

      4. \[ \begin{align*} P\left( |X| \geq 2 \right) &= P(X \leq - 2) + P(X \geq 2) \\ &= F( - 2) + 1 - P(X < 2) \\ &= 0.02 + 1 - P(X \leq 2) \\ &= 0.02 + 1 - 0.98 = 0.04 \end{align*} \]

  3. Sei X eine diskrete Zufallsvariable mit folgender Wahrscheinlichkeitsfunktion:

    \[x_{j}\] -10 0 1 2 99
    \[f\left( x_{j} \right)\] 0.1 0.4 0.1 0.3 0.1

    Geben Sie die Verteilungsfunktion von X in Form einer Tabelle an.

    \[x_{j}\] -10 0 1 2 99
    \[F\left( x_{j} \right)\] 0.1 0.5 0.6 0.9 1

  4. Sei X eine diskrete Zufallsvariable mit folgender Verteilungsfunktion:

    \[x_{j}\] 1 2 3 4 5
    \[F\left( x_{j} \right)\] 0.1 0.4 0.5 0.9 1

    Geben Sie die Wahrscheinlichkeitsfunktion von X in Form einer Tabelle an.

    \[x_{j}\] 1 2 3 4 5
    \[f\left( x_{j} \right)\] 0.1 0.3 0.1 0.4 0.1

  5. Sei X eine diskrete Zufallsvariable mit folgender Wahrscheinlichkeitsfunktion:

    \[x_{j}\] -2 -1 0 1 2
    \[f\left( x_{j} \right)\] 0.1 0.3 0.4 0 0.2

    1. Berechnen Sie den Erwartungswert von X.

      \[\begin{align*} E(X) &= \sum_{j = 1}^{m}{x_{j} \cdot f( x_{j} )} \\ &= (-2 \cdot 0.1) + (-1 \cdot 0.3) + (0 \cdot 0.4) + (1 \cdot 0) + (2 \cdot 0.2) \\ &= - 0.1 \end{align*}\]

    2. Berechnen Sie die Varianz von X.

      \[\begin{align*} Var(X) &= \sum_{j = 1}^{m}{( x_{j} - E(X) )^{2} \cdot f( x_{j} )} \\ &= (-2 + 0.1)^2 \cdot 0.1 + (-1 + 0.1)^2 \cdot 0.3 + (0 + 0.1)^2 \cdot 0.4 + (1 + 0.1)^2 \cdot 0 + (2 + 0.1)^2 \cdot 0.2 \\ &= 1.49 \end{align*}\]

    3. Berechnen Sie die Standardabweichung von X.

      \[SD(X) = \sqrt{Var(X)} = \sqrt{1.49} = 1.22\]

  6. Sie werfen einen fairen sechsseitigen Würfel dreimal. Hierbei nehmen die Bernoulli-Variablen \(X_{i}\) für i = 1, 2, 3 jeweils den Wert 1 an, falls Sie im i-ten Wurf eine 6 würfeln, und den Wert 0, falls nicht. Sie können davon ausgehen, dass diese drei Zufallsvariablen unabhängig sind. Die Zufallsvariable \(X\) steht für die Anzahl an gewürfelten Sechsern, also \(X = X_{1} + X_{2} + X_{3}\)

    1. Geben Sie den Träger \(T_{X_{1}}\) von \(X_{1}\) an.

      \[T_{X_{1}} = \left\{ 0,\ 1 \right\}\]

    2. Welcher Wahrscheinlichkeitsverteilung folgt \(X_{1}\)? Geben Sie diese in Form einer Tabelle an.

      \(X_{1}\) folgt einer Bernoulli-Verteilung mit \(\pi = \frac{1}{6}\) , also

      \[X_{1}\ \sim\ Be\left( \frac{1}{6} \right)\]

      \[A_{X_{1}}\] \[\{\}\] \[\left\{ 0 \right\}\] \[\left\{ 1 \right\}\] \[T_{X_{1}}\]
      \[P_{X_{1}}\left( A_{X_{1}} \right)\] 0 \[\frac{5}{6}\] \[\frac{1}{6}\] 1

    3. Geben Sie die Wahrscheinlichkeitsfunktion von \(X_{1}\) in Form einer Gleichung an.

      \[f\left( x_{j} \right) = \pi^{x_{j}}(1 - \pi)^{1 - x_{j}} = \left( \frac{1}{6} \right)^{x_{j}}\left( \frac{5}{6} \right)^{1 - x_{j}}\]

    4. Berechnen Sie den Erwartungswert, die Varianz und die Standardabweichung von \(X_{1}\).

      \[E\left( X_{1} \right) = \pi = \frac{1}{6}\]

      \[Var\left( X_{1} \right) = \pi(1 - \pi) = \frac{1}{6} \cdot \frac{5}{6} = \frac{5}{36} \approx 0.14\]

      \[SD\left( X_{1} \right) = \sqrt{Var\left( X_{1} \right)} = \sqrt{\frac{5}{36}} \approx 0.37\]

    5. Geben Sie den Träger von \(X\) an.

      \[T_{X} = \left\{ 0,\ 1,\ 2,\ 3 \right\}\]

    6. Welcher Wahrscheinlichkeitsverteilung folgt \(X\)?

      X folgt einer Binomialverteilung mit \(n = 3\) und \(\pi = \frac{1}{6}\) , also

      \[X\ \sim\ B\left( 3,\ \frac{1}{6} \right)\]

    7. Geben Sie die Wahrscheinlichkeitsfunktion von \(X\) in Form einer Gleichung an.

      \[f\left( x_{j} \right) = \binom{n}{x_{j}}\pi^{x_{j}}(1 - \pi)^{n - x_{j}} = \binom{3}{x_{j}}\left( \frac{1}{6} \right)^{x_{j}}\left( \frac{5}{6} \right)^{3 - x_{j}}\]

    8. Geben Sie die Verteilungsfunktion von \(X\) in Form einer Gleichung an.

      \[F\left( x_{k} \right) = \sum_{j = 1}^{k}{f\left( x_{j} \right) =}\sum_{j = 1}^{k}{\binom{n}{x_{j}}\pi^{x_{j}}(1 - \pi)^{n - x_{j}}} = \sum_{j = 1}^{k}{\binom{3}{x_{j}}\left( \frac{1}{6} \right)^{x_{j}}\left( \frac{5}{6} \right)^{3 - x_{j}}}\]

    9. Berechnen Sie den Erwartungswert, die Varianz und die Standardabweichung von \(X\).

      \[E(X) = n\pi = 3 \cdot \frac{1}{6} = 0.5\]

      \[Var(X) = n\pi(1 - \pi) = 3 \cdot \frac{1}{6} \cdot \frac{5}{6} = \frac{15}{36} \approx 0.42\]

      \[SD(X) = \sqrt{Var(X)} = \sqrt{\frac{15}{36}} \approx 0.65\]

    10. Berechnen Sie die Wahrscheinlichkeiten für die folgenden Ereignisse:

      1. Ereignis 1: Sie würfeln drei Sechser

        \[P(X = 3) = f(3) = \binom{3}{3}\left( \frac{1}{6} \right)^{3}\left( \frac{5}{6} \right)^{3 - 3} = \frac{1}{216} \approx 0.005\]

      2. Ereignis 2: Sie würfeln keine Sechs

        \[P(X = 0) = f(0) = \binom{3}{0}\left( \frac{1}{6} \right)^{0}\left( \frac{5}{6} \right)^{3 - 0} = \frac{125}{216} \approx 0.58\]

      3. Ereignis 3: Sie würfeln mindestens zwei Sechser

        \[ \begin{align*} P(X \geq 2) &= f(2) + f(3) \\ &= \binom{3}{2}\left( \frac{1}{6} \right)^{2}\left( \frac{5}{6} \right)^{3 - 2} + \frac{1}{216} \\ &= 3 \cdot \frac{1}{36} \cdot \frac{5}{6} + \frac{1}{216} \\ &= \frac{15}{216} + \frac{1}{216} = \frac{16}{216} \approx 0.07 \end{align*} \]

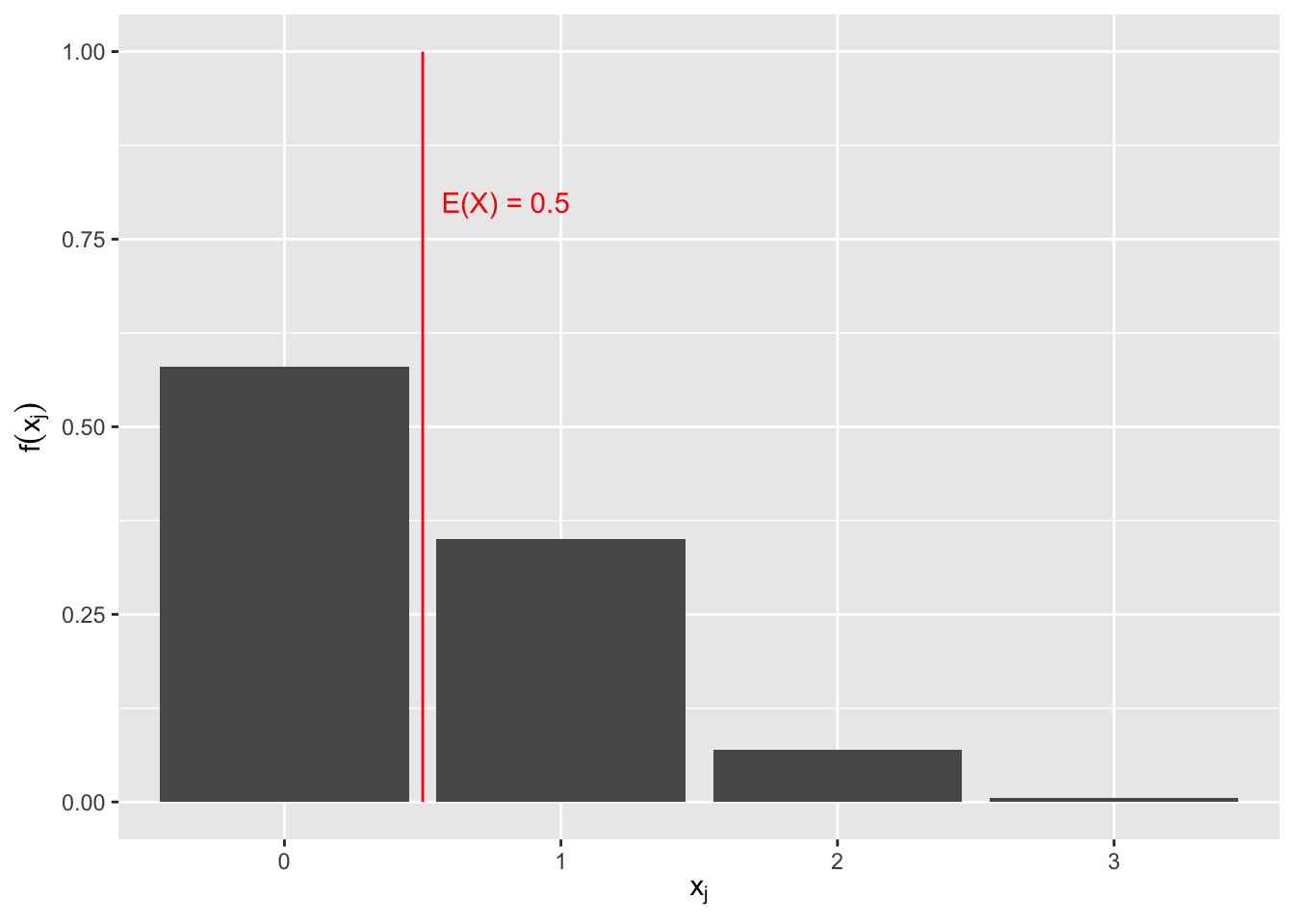
    11. Stellen Sie die Wahrscheinlichkeitsfunktion von \(X\) graphisch dar. Beschriften Sie hierbei die Achsen und veranschaulichen Sie den Erwartungswert.

      \(f(0) \approx 0.58\) (siehe Teilaufgabe j ii)

      \(f(1) = \binom{3}{1}\left( \frac{1}{6} \right)^{1}\left( \frac{5}{6} \right)^{3 - 1} = 3 \cdot \frac{1}{6} \cdot \left( \frac{5}{6} \right)^{2} = \frac{75}{216} \approx 0.35\)

      \(f(2) = \frac{15}{216} \approx 0.07\) (siehe Teilaufgabe j iii)

      \(f(3) \approx 0.005\) (siehe Teilaufgabe j i)

      x-Achse von 0 bis 3 in ganzen Schritten und y-Achse von 0 bis 1 in 0.25 Schritten, es ist ein Säulenendiagramm abgebildet. Die Höhe der Säulen entspricht den zuvor berechneten Werten von f(0) bis f(3). Der Erwartungswert ist bei x = 0.5 eingezeichnet.

    12. In R können Sie sich die Werte der Wahrscheinlichkeitsfunktion und der Verteilungsfunktion beliebiger binomialverteilter Zufallsvariablen ausgeben lassen.

      Wahrscheinlichkeitsfunktion:

      dbinom(x, n, pi)

      Verteilungsfunktion:

      pbinom(x, n , pi)

      Berechnen Sie die Wahrscheinlichkeiten aus Teilaufgabe j mithilfe dieser Funktionen in R.

      ## Wahrscheinlichkeitsfunktion der Binomialverteilung mit n=3 und p=1/6:
n <- 3
p <- 1 / 6

dbinom(0, n, p)
      [1] 0.5787037
      dbinom(1, n, p)
      [1] 0.3472222
      dbinom(2, n, p)
      [1] 0.06944444
      dbinom(3, n, p)
      [1] 0.00462963
      ## Alle Werte der Wahrscheinlichkeitsfunktion als Vektor:
x_j <- 0:3
dbinom(x_j, n, p)
      [1] 0.57870370 0.34722222 0.06944444 0.00462963
      ## Verteilungsfunktion der Binomialvereilung mit n=3 und p=1/6:
n <- 3
p <- 1 / 6

pbinom(0, n, p)
      [1] 0.5787037
      pbinom(1, n, p)
      [1] 0.9259259
      pbinom(2, n, p)
      [1] 0.9953704
      pbinom(3, n, p)
      [1] 1
      ## Alle Werte der Verteilungsfunktion als Vektor:
x_j <- 0:3
pbinom(x_j, n, p)
      [1] 0.5787037 0.9259259 0.9953704 1.0000000
      ## Berechnung der Wahrscheinlichkeiten aus Teilaufgabe j:
n <- 3
p <- 1 / 6

dbinom(3, n, p)
      [1] 0.00462963
      dbinom(0, n, p)
      [1] 0.5787037
      dbinom(2, n, p) + dbinom(3, n, p)
      [1] 0.07407407

    13. Mithilfe der Funktion rbinom() können Sie unabhängige Realisationen von Zufallsvariablen mit beliebiger Binomialverteilung zufällig in R erzeugen:

      rbinom(Anzahl der unabhängigen Realisationen, n, pi)

      Erzeugen Sie 1 Million Realisationen von \(X\), speichern Sie diese in einem Vektor mit dem Namen x ab:

      x <- rbinom(1000000, 3, 1/6)

      Berechnen Sie den Mittelwert \(\bar{x}\), die Varianz \(s^2\) und die Standardabweichung \(s\) der zufällig gezogenen Realisationen. Was fällt Ihnen auf?

      ## einzelne zufällige Realisationen:
n <- 3
p <- 1 / 6

rbinom(1, n, p)
      [1] 0
      rbinom(1, n, p)
      [1] 0
      rbinom(1, n, p)
      [1] 0
      ## 1 Million zufällige Realisationen:
x <- rbinom(1000000, n, p)
mean(x)
      [1] 0.49916
      var(x)
      [1] 0.4158997
      sd(x)
      [1] 0.6449029
      ## Erwartungswert, Varianz und Standardabweichung:
n * p
      [1] 0.5
      n * p * (1 - p)
      [1] 0.4166667
      sqrt(n * p * (1 - p))
      [1] 0.6454972

      Der Wert \(\bar{x}\) liegt sehr nahe an dem in Teilaufgabe i berechneten Erwartungswert. Der Wert \(s^2\) liegt sehr nahe an der in Teilaufgabe i berechneten Varianz. Der Wert \(s\) liegt sehr nahe an der in Teilaufgabe i berechneten Standardabweichung.

      Dies veranschaulicht die Interpretation von Erwartungswert, Varianz und Standardabweichung als Mittelwert, empirische Varianz und empirische Standardabweichung der Realisationen bei unendlicher Wiederholung des zugrundeliegenden Zufallsexperiments.

  7. Bonusaufgabe: Sei \(X\) eine diskrete Zufallsvariable mit Träger \(T_X = \{-2, -1, 0, 1, 2\}\) und Erwartungswert \(E(X) = 1\).

    Welche der folgenden Aussagen können Sie auf Basis dieser Information treffen?

    1. Es ist wahrscheinlicher, dass sich die Zufallsvariable in einem positiven Wert realisiert, als in einem Wert gleich oder kleiner 0.

      Falsch, diese Aussage kann nur getroffen werden, wenn man die genaue Wahrscheinlichkeitsfunktion von X kennt. Gegenbeispiel:

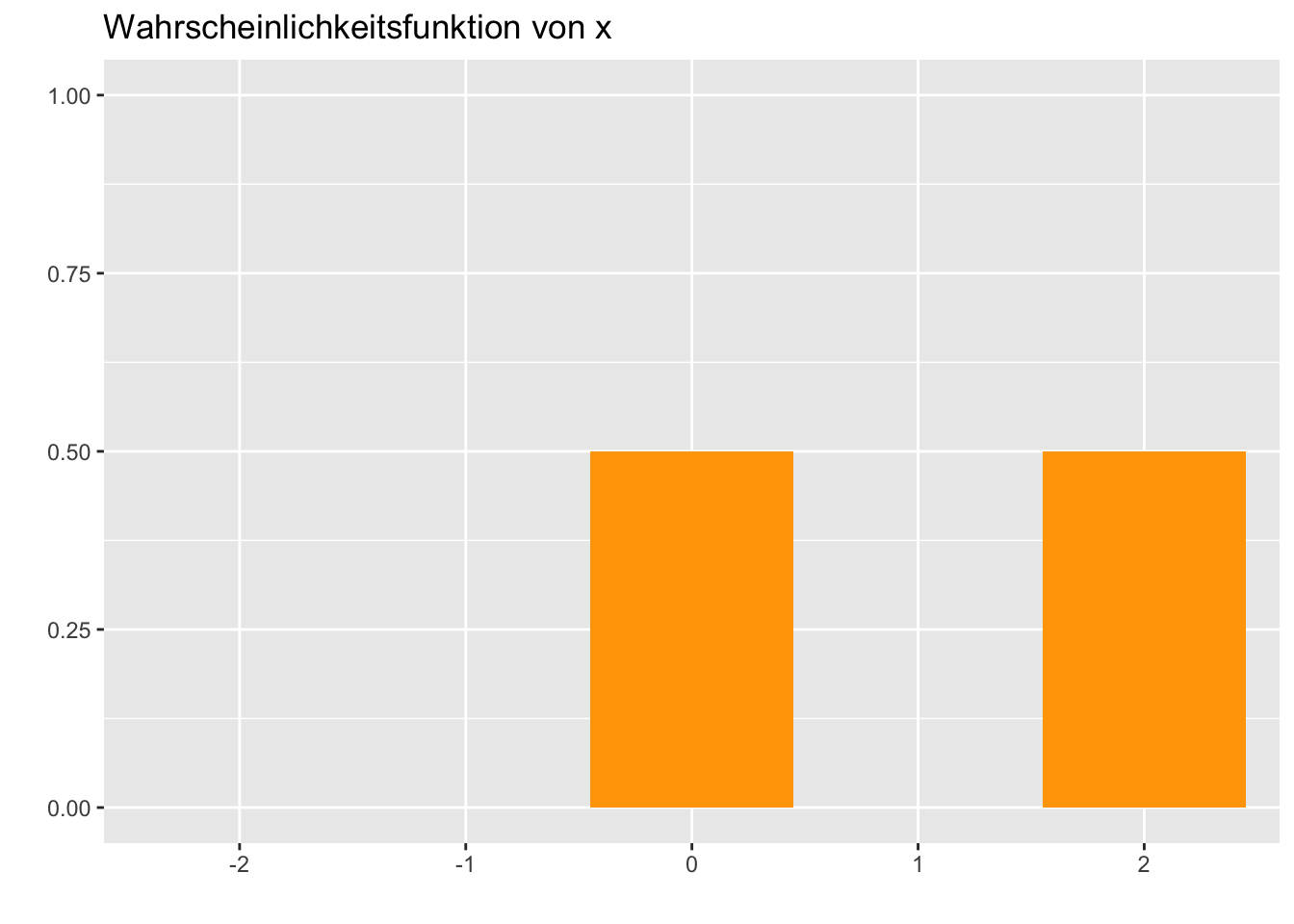
      Alternativtext

      \[E(X) = \sum_{j = 1}^{m}{x_{j} \cdot f\left( x_{j} \right) = ( - 2) \cdot 0 + ( - 1) \cdot 0 + 0 \cdot 0,5 + 1 \cdot 0 + 2 \cdot 0,5 = 1}\]

      aber \(P(X > 0) = P(X \leq 0) = 0.5\)

    2. Es ist am wahrscheinlichsten, dass die Zufallsvariable den Wert 1 annimmt.

      Falsch, auch diese Aussage kann nur getroffen werden, wenn man die genaue Wahrscheinlichkeitssfunktion von X kennt. Gegenbeispiel:

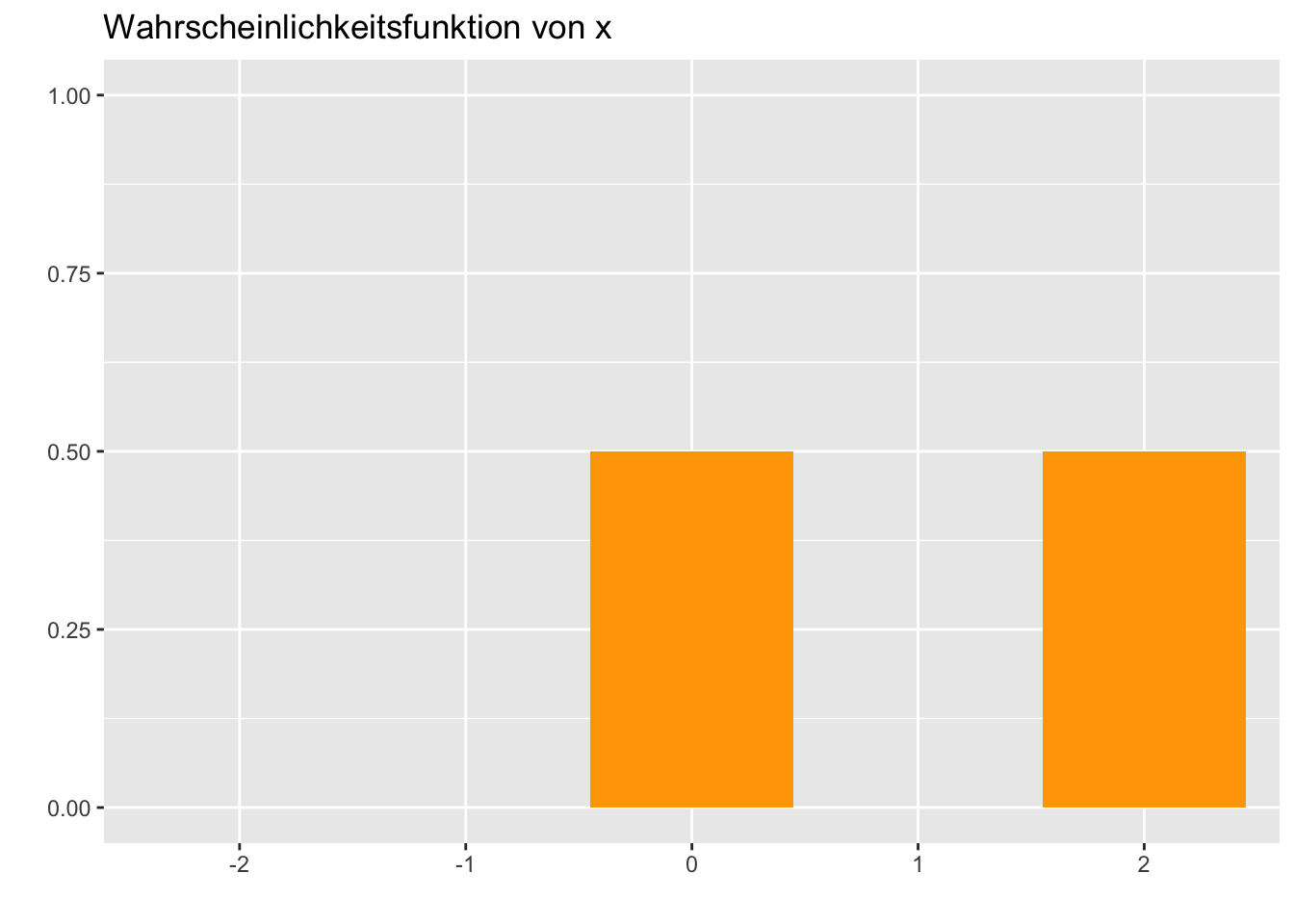
      Alternativtext

      \(E(X) = 1\) aber \(P(X = 1) = 0\)

    3. Würde man den durch die Zufallsvariable repräsentierten Zufallsvorgang unendlich oft wiederholen, wäre die durchschnittliche Realisation gleich 1.

      Richtig, dies ist die Interpretation des Erwartungswerts.

  8. Bonusaufgabe:

    Sei X eine stetige Zufallsvariable mit Träger \(T_{X} = \lbrack 0,\ 1\rbrack\) und folgender Wahrscheinlichkeitsdichtefunktion:

    \(f(x) = 1\) für alle \(x \in T_{X}\)

    Dies ist die Dichtefunktion der stetigen Gleichverteilung auf dem Intervall \(\lbrack 0,\ 1\rbrack\).

    1. Veranschaulichen Sie diese Wahrscheinlichkeitsdichtefunktion graphisch.

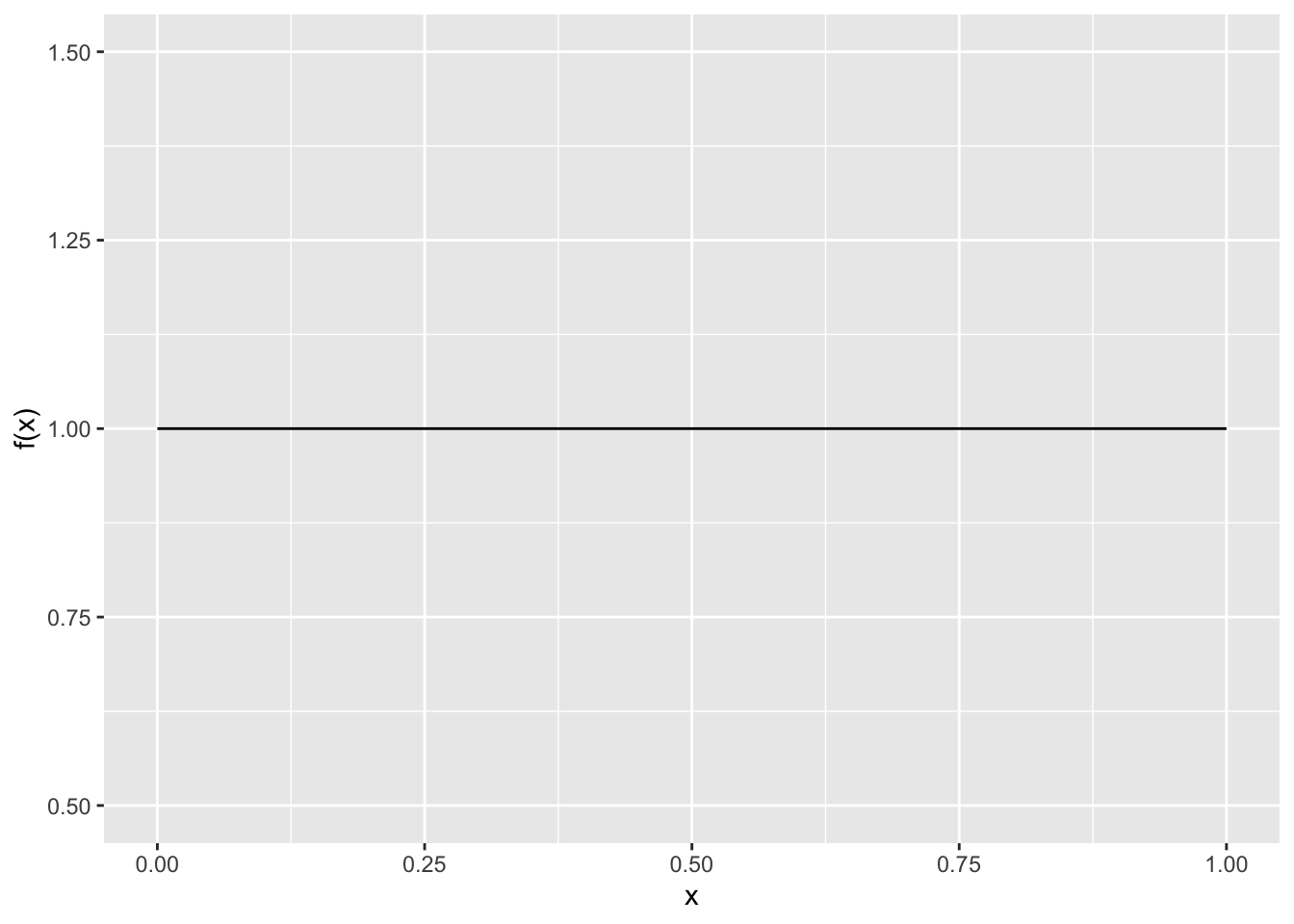
      x-Achse von 0.5 bis 1.5 in 0.25 Schritten und y-Achse von 0 bis 1 in 0.25 Schritten. Eine horizontale Gerade ist bei y=1 eingezeichnet.

    2. Berechnen Sie die folgenden Wahrscheinlichkeiten (Hinweis: Sie benötigen das Wissen aus der Schule, wie Sie eine Stammfunktion bilden):

      1. \(P_{X}\left( \lbrack 0.5,\ 1\rbrack \right)\)

        \[P_{X}\left( \lbrack 0.5,\ 1\rbrack \right) = \int_{0.5}^{1}{f(x)dx} = \int_{0.5}^{1}{1dx} = \lbrack x\rbrack_{0.5}^{1} = 1 - 0.5 = 0.5\]

      2. \(P_{X}\left( \lbrack 0.4,\ 0.6\rbrack \right)\)

        \[P_{X}\left( \lbrack 0.4,\ 0.6\rbrack \right) = \int_{0.4}^{0.6}{f(x)dx} = \int_{0.4}^{0.6}{1dx} = \lbrack x\rbrack_{0.4}^{0.6} = 0.6 - 0.4 = 0.2\]

      3. \(P_{X}\left( \lbrack 0,\ 0.1\rbrack \cup \lbrack 0.9,\ 1\rbrack \right)\)

        \[ \begin{align*} P_{X}\left( \lbrack 0,\ 0.1\rbrack \cup \lbrack 0.9,\ 1\rbrack \right) &= P_{X}\left( \lbrack 0,\ 0.1\rbrack \right) + P_{X}\left( \lbrack 0.9,\ 1\rbrack \right) \\ &= \int_{0}^{0.1}{f(x)dx} + \int_{0.9}^{1}{f(x)dx} \\ &= \int_{0}^{0.1}{1dx} + \int_{0.9}^{1}{1dx} \\ &= \lbrack x\rbrack_{0}^{0.1} + \lbrack x\rbrack_{0.9}^{1} \\ &= 0.1 - 0 + 1 - 0.9 = 0.2 \end{align*} \]

    3. Bestimmen Sie die Verteilungsfunktion von X und veranschaulichen Sie diese graphisch.

      \[F(x) = \int_{0}^{x}{f(y)dy} = \int_{0}^{x}{f(y)dy} = \lbrack y\rbrack_{0}^{x} = x - 0 = x\]

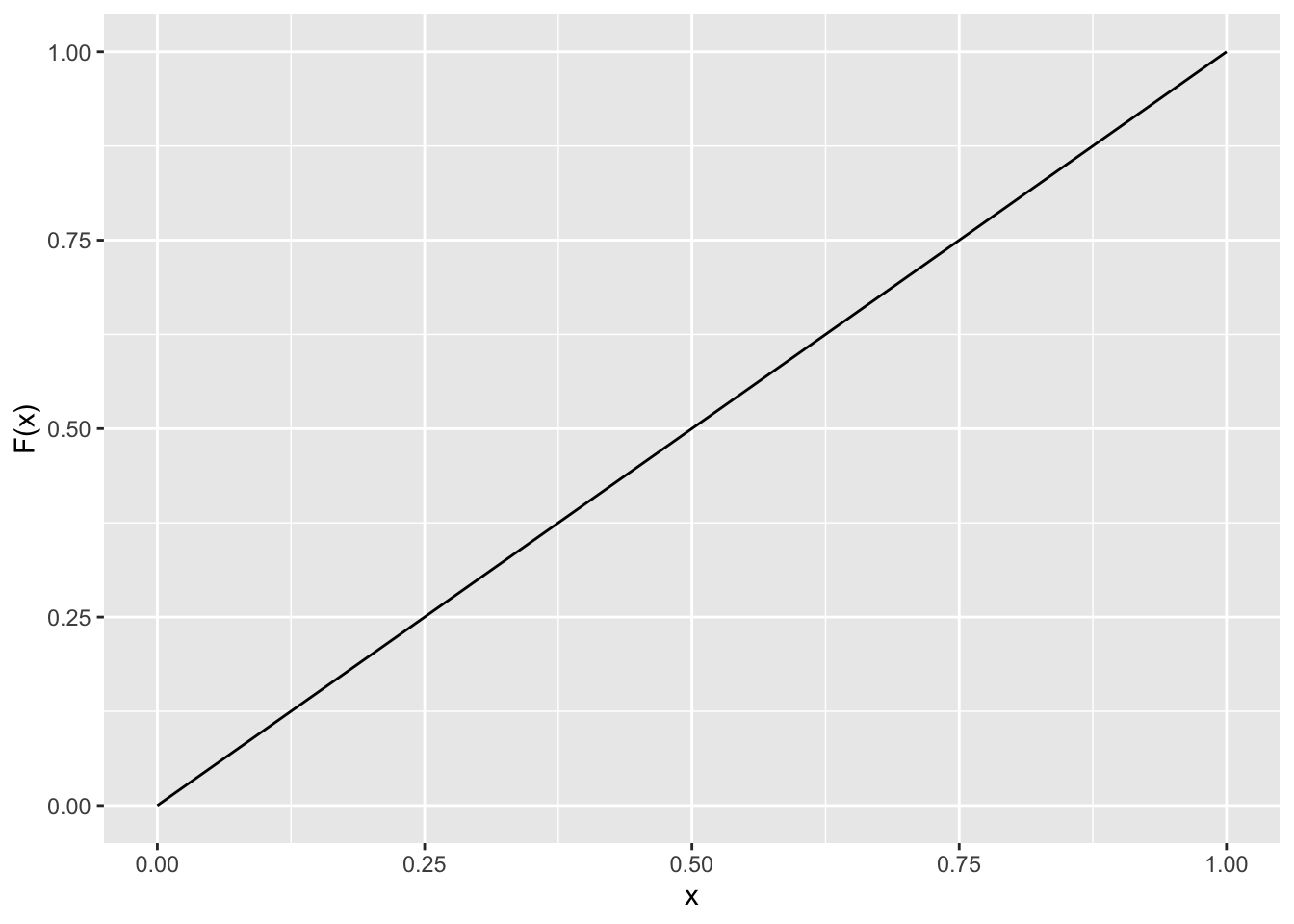
      x-Achse von 0 bis 1 in 0.25 Schritten und y-Achse von 0 bis 1 in 0.25 Schritten. Eine Gerade mit Ursprung (0|0) und einer Steigung von 1 ist eingezeichnet.

    4. Berechnen Sie den Erwartungswert von X.

      \[E(X) = \int_{0}^{1}{x \cdot f(x)dx} = \int_{0}^{1}{x \cdot 1dx} = \int_{0}^{1}{xdx} = \left\lbrack \frac{1}{2}x^{2} \right\rbrack_{0}^{1} = \frac{1}{2} - 0 = \frac{1}{2}\]

    5. Berechnen Sie die Varianz von X.

      \[ \begin{align*} Var(X) &= \int_{0}^{1}{\left( x - E(X) \right)^{2} \cdot f(x)dx} \\ &= \int_{0}^{1}{\left( x - \frac{1}{2} \right)^{2} \cdot 1dx} \\ &= \int_{0}^{1}{\left( x^{2} - x + \frac{1}{4} \right)dx} \\ &= \int_{0}^{1}{x^{2}dx} - \int_{0}^{1}{xdx} + \int_{0}^{1}{\frac{1}{4}dx} \\ &= \left\lbrack \frac{1}{3}x^{3} \right\rbrack_{0}^{1} - \left\lbrack \frac{1}{2}x^{2} \right\rbrack_{0}^{1} + \left\lbrack \frac{1}{4}x \right\rbrack_{0}^{1} \\ &= \frac{1}{3} - 0 - \frac{1}{2} + 0 + \frac{1}{4} - 0 \\ &= \frac{1}{3} - \frac{1}{2} + \frac{1}{4} = \frac{1}{12} \end{align*} \]

  9. Bonusaufgabe:

    Zeigen Sie, dass Varianz und Standardabweichung einer z-standardisierten Zufallsvariable Z jeweils gleich 1 sind. Hinweis: Verwenden Sie die Rechenregeln für Varianzen.

    \[Var(Z) = Var\left( \frac{X - E(X)}{SD(X)} \right) = \frac{1}{{SD(X)}^{2}}Var\left( X - E(X) \right) = \frac{1}{Var(X)}Var(X) = 1\]

    \[SD(Z) = \sqrt{Var(Z)} = \sqrt{1} = 1\]