Übungsblatt 06

Normalverteilung, einfache Zufallsstichprobe, Schätzfunktionen und Schätzgütekriterien

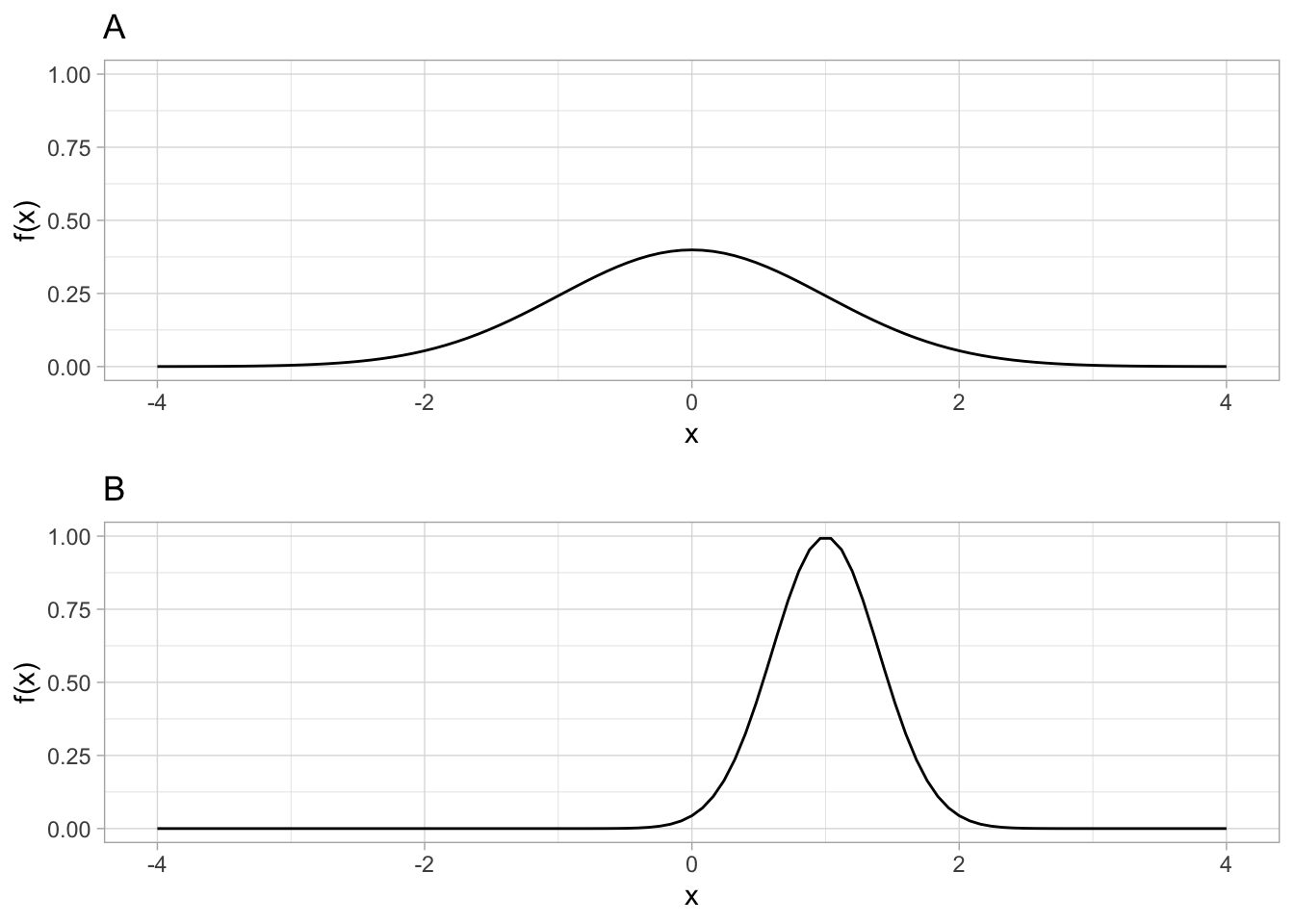
  1. Im Folgenden sind die Wahrscheinlichkeitsdichtefunktionen zweier unterschiedlicher normalverteilter Zufallsvariablen dargestellt:

    A: x-Achse von -4 bis 4 in ganzen Schritten, y-Achse von 0 bis 1 in 0.25 Schritten. Es ist eine Normalverteilung eingezeichnet, die ihren Höhepunkt bei (0|0.4) hat. B: x-Achse von -4 bis 4 in ganzen Schritten, y-Achse von 0 bis 1 in 0.25 Schritten. Es ist eine Normalverteilung eingezeichnet, die ihren Höhepunkt bei (1|1) hat.

    1. Welche der beiden Zufallsvariablen hat einen höheren Erwartungswert?

      Der Erwartungswert einer normalverteilten Zufallsvariable entspricht dem Parameter \(\mu\). \(\mu\) entspricht wiederum dem Wert auf der x-Achse, bei dem die Wahrscheinlichkeitsdichtefunktion der Zufallsvariablen maximal ist. Das Maximum der Wahrscheinlichkeitsdichtefunktion der zweiten Zufallsvariable liegt weiter rechts. Daher hat die zweite Zufallsvariable einen höheren Erwartungswert.

    2. Welche der beiden Zufallsvariablen hat eine höhere Varianz?

      Die Varianz einer normalverteilten Zufallsvariable entspricht dem Parameter \(\sigma^{2}\). \(\sigma^{2}\) bestimmt wiederum die Breite der Wahrscheinlichkeitsdichtefunktion der Zufallsvariablen. Die Wahrscheinlichkeitsdichtefunktion der ersten Zufallsvariable ist breiter. Daher hat die erste Zufallsvariable eine höhere Varianz.

  2. Sei \(X\) eine stetige Zufallsvariable, die für den IQ einer zufällig gezogenen erwachsenen Person steht. Gehen Sie davon aus, dass \(X\) normalverteilt ist mit \(\mu = 100\) und \(\sigma^{2} = 225\). Berechnen Sie die folgenden Wahrscheinlichkeiten mithilfe der Verteilungsfunktion. In R können Sie sich die Werte der Verteilungsfunktion beliebiger normalverteilter Zufallsvariablen mit der Funktion pnorm(x, mean = mu, sd = sigma) ausgeben lassen.

    1. Wie hoch ist die Wahrscheinlichkeit, dass die zufällig gezogene Person hochbegabt ist, d.h. einen IQ > 130 hat?

      \(P(IQ > 130) = 1 - P(IQ \leq 130) = 1 - F(130)\):

      1 - pnorm(130, mean = 100, sd = 15)
      [1] 0.02275013

    2. Wie hoch ist die Wahrscheinlichkeit, dass die zufällig gezogene Person einen IQ zwischen 85 und 115 hat?

      \(P(85 \leq IQ \leq 115) = P(IQ \leq 115) - P(IQ \leq 85) = F(115) - F(85)\):

      pnorm(115, mean = 100, sd = 15) - pnorm(85, mean = 100, sd = 15)
      [1] 0.6826895

    3. Wie hoch ist die Wahrscheinlichkeit, dass die zufällig gezogene Person einen extremen IQ (mehr als 2 Standardabweichungen unter oder über dem Mittelwert) aufweist?

      Hinweis: Das Zeichen \(\lor\) steht für eine ODER-Verknüpfung.

      \[\begin{align*} P(IQ > 100 + 2 \cdot 15 \lor IQ < 100 - 2 \cdot 15) &= P(IQ > 130 \lor IQ < 70)\\ &= P(IQ > 130) + P(IQ < 70) \\ &= 1 - P(IQ \leq 130) + P(IQ < 70) \\ &= 1 - F(130) + F(70) \end{align*}\]

      1 - pnorm(130, mean = 100, sd = 15) + pnorm(70, mean = 100, sd = 15)
      [1] 0.04550026

      Da die Normalverteilung symmetrisch ist, können wir auch einfach eine der beiden Wahrscheinlichkeiten \(P(IQ > 130)\) bzw. \(P(IQ < 70)\) berechnen und den Wert verdoppeln:

      \[\begin{align*} P(IQ > 100 + 2 \cdot 15 \lor IQ < 100 - 2 \cdot 15) &= P(IQ > 130 \lor IQ < 70)\\ &= 2 \cdot P(IQ < 70) \\ &= 2 \cdot F(70) \end{align*}\]

      2 * pnorm(70, mean = 100, sd = 15)
      [1] 0.04550026

    4. Mithilfe der Funktion rnorm() können Sie unabhängige Realisationen von Zufallsvariablen mit beliebiger Normalverteilung zufällig in R erzeugen:

      rnorm(Anzahl der unabhängigen Realisationen, mean = mu, sd = sigma)

      Erzeugen Sie 1 Million Realisationen von \(X\), speichern Sie diese in einem Vektor mit dem Namen x ab:

      x <- rnorm(1000000, mean = 100, sd = 15)

      Berechnen Sie den Mittelwert \(\bar{x}\), die Varianz \(s^2\) und die Standardabweichung \(s\) der zufällig gezogenen Realisationen. Was fällt Ihnen auf?

      ## einzelne zufällige Realisationen:
mu <- 100
sigma <- 15

rnorm(1, mean = mu, sd = sigma)
      [1] 110.3178
      rnorm(1, mean = mu, sd = sigma)
      [1] 86.92486
      rnorm(1, mean = mu, sd = sigma)
      [1] 99.31335
      ## 1 Million zufällige Realisationen:
x <- rnorm(1000000, mean = 100, sd = 15)
mean(x)
      [1] 99.99477
      var(x)
      [1] 224.6223
      sd(x)
      [1] 14.98741

      Der Wert \(\bar{x}\) liegt sehr nahe an dem Erwartungswert \(\mu = 100\). Der Wert \(s^2\) liegt sehr nahe an der Varianz \(\sigma^2 = 225\). Der Wert \(s\) liegt sehr nahe an der Standardabweichung \(\sigma = 15\).

      Dies veranschaulicht die Interpretation von Erwartungswert, Varianz und Standardabweichung als Mittelwert, empirische Varianz und empirische Standardabweichung der Realisationen bei unendlicher Wiederholung des zugrundeliegenden Zufallsexperiments.

  3. BONUS: Zeigen Sie, dass im Fall von Messwerten \(x_{1}\), \(x_{2}\), …, \(x_{n}\), die jeweils nur die Messwertausprägungen 0 und 1 annehmen können, \[\overline{x} = \frac{1}{n}\sum_{i = 1}^{n}x_{i} = h(1)\] ist.

    \[\overline{x} = \frac{1}{n}\sum_{i = 1}^{n}x_{i} = \frac{1}{n}(0 + 0 + \ldots + 0 + 1 + 1 + \ldots + 1) = \frac{1}{n}(1 + 1 + \ldots + 1) = \frac{H(1)}{n} = h(1)\]

  4. Sie interessieren sich für die relative Häufigkeit von Zwangsstörungen in Deutschland. Sie ziehen zufällig und unabhängig voneinander n Person aus der Population, wobei jedoch alle Personen, die nicht PsychologiestudentInnen sind, eine Wahrscheinlichkeit von Null haben, in die Stichprobe gezogen zu werden. Alle PsychologiestudentInnen haben die gleiche (positive) Wahrscheinlichkeit gezogen zu werden. Sie betrachten die Zufallsvariablen \(X_{1}\), \(X_{2}\), …, \(X_{i}\), …, \(X_{n}\), welche jeweils den Wert 1 annehmen, falls die zufällig gezogene Person i unter einer Zwangsstörung leidet, und den Wert 0, falls nicht.

    1. Welcher Wahrscheinlichkeitsverteilung folgen die Zufallsvariablen \(X_{1}\), \(X_{2}\), …, \(X_{i}\), …, \(X_{n}\) jeweils?

      Die Stichprobe ist immer noch eine einfache Zufallsstichprobe, jedoch nur aus der Teilpopulation der PsychologiestudentInnen. Für die Zufallsvariablen gilt: \(X_{i}\ \sim\ Be(\pi)\) für alle i = 1, 2, …, n

    2. Welcher deskriptivstatistischen Maßzahl in welcher Population entspricht der Parameter dieser Verteilung?

      Der relativen Häufigkeit der Zwangsstörung bei PsychologiestudentInnen.

    3. Welches Problem liegt hier bei der Stichprobenziehung vor?

      Fehlende Repräsentativität.

  5. Erklären Sie die Begriffe Parameter, Schätzfunktion und Schätzwert.

    Parameter legen die konkrete Verteilung einer Zufallsvariable fest. Zum Beispiel besitzt die Bernoulli-Verteilung den Parameter \(\pi\). Kennt man den genauen Wert von \(\pi\), kennt man die konkrete Wahrscheinlichkeitsverteilung einer Bernoulli-Variablen. Kennt man den Wert des Parameters \(\pi\) nicht, so ist nur die allgemeine „Form” der Wahrscheinlichkeitsverteilung bekannt: Man weiß nur, dass die Zufallsvariable bernoulliverteilt ist mit irgendeinem Parameterwert \(\pi\).

    Hat man Daten aus einer einfachen Zufallsstichprobe vorliegen und weiß, welcher allgemeinen Verteilung die einzelnen Zufallsvariablen folgen (z.B. Bernoulli-Verteilung), kann man versuchen, aus den Daten Rückschlüsse auf die Parameterwerte der konkreten Verteilung der Zufallsvariablen zu ziehen. Eine Schätzfunktion ist bei diesem Vorgehen eine Zufallsvariable, deren Realisationen konkrete Schätzwerte für den Parameter sind. Ein Schätzwert ist die Realisation einer Schätzfunktion für eine bestimmte Stichprobe und somit eine konkrete Zahl.

    Bsp.: Die Zufallsvariablen Xi mit i = 1, 2, ..., n seien iid bernoulliverteilt. Der Parameter der Bernoulliverteilung ist \(\pi\). Als Schätzfunktion für \(\pi\) verwenden wir die Zufallsvariable \(\overline{X}\), da diese eine erwartungstreue, effiziente und konsistente Schätzfunktion für \(\pi\) ist. Der konkrete Schätzwert für \(\pi\) ist die Realisation \(\overline{x}\) der Schätzfunktion \(\overline{X}\) in unserer konkreten Stichprobe.

  6. Sie betrachten eine Population, die aus den Personen Anna, Paul, Paula, Peter, Petra und Detlev besteht. Sie ziehen eine einfache Zufallsstichprobe der Größe n = 3 aus dieser Population.

    1. Geben Sie zwei mögliche Ergebnisse dieses Zufallsexperiments an.

      Zum Beispiel:

      Anna, Peter, Petra

      oder:

      Peter, Paul, Paula

    2. Seien \(X_{1}\), \(X_{2}\), \(X_{3}\) Zufallsvariablen, die jeweils den Wert 1 annehmen, falls der Name der ersten, zweiten, dritten gezogenen Person auf a endet. Welcher Wahrscheinlichkeitsverteilung folgen die Zufallsvariablen?

      \(X_{i}\ \sim\ Be(0.5)\) für alle i = 1, 2, 3

    3. Welcher deskriptivstatistischen Maßzahl in der Population entspricht der Parameter dieser Verteilung?

      Der relativen Häufigkeit von Personen, deren Namen auf a enden in der Population.

    4. Sie betrachten die Schätzfunktion \(\overline{X}\) für den Parameter der Wahrscheinlichkeitsverteilung von \(X_{1}\), \(X_{2}\) und \(X_{3}\). Geben Sie den Träger von \(\overline{X}\) an.

      \[T_{\overline{X}} = \left\{ 0,\ \frac{1}{3},\ \frac{2}{3},\ 1 \right\}\]

    5. Berechnen Sie den Erwartungswert von \(\overline{X}\). Interpretieren Sie diesen.

      \[E\left( \overline{X} \right) = \pi = 0.5\]

      Falls man unendlich oft eine Stichprobe der Größe n = 3 aus der Population ziehen würde und jedes Mal den Schätzwert \(\overline{x}\) in der gezogenen Stichprobe berechnen würde, wäre der Mittelwert aller dieser Schätzwerte 0.5, würde also dem wahren Parameterwert \(\pi\) = 0.5 entsprechen.

    6. Berechnen Sie den Standardfehler von \(\overline{X}\). Interpretieren Sie diesen.

      \[SE\left( \overline{X} \right) = \sqrt{\frac{\pi(1 - \pi)}{n}} = \sqrt{\frac{0.5(1 - 0.5)}{3}} \approx 0.29\]

      Falls man unendlich oft eine Stichprobe der Größe n = 3 aus der Population ziehen würde und jedes Mal den Schätzwert \(\overline{x}\) in der gezogenen Stichprobe berechnen würde, wäre die empirische Standardabweichung aller dieser Schätzwerte 0.29.

    7. Berechnen Sie für Ihre Ergebnisse aus Teilaufgabe a jeweils den konkreten Schätzwert.

      Anna, Peter, Petra: \(\overline{x} = \frac{2}{3}\)

      Peter, Paul, Paula: \(\overline{x} = \frac{1}{3}\)

  7. Gesucht ist der Anteil der Personen in Deutschland, bei denen im letzten Jahr eine Angststörung diagnostiziert wurde.

    1. Ihnen liegt eine einfache Zufallsstichprobe mit Umfang n = 500 vor. Nennen Sie eine geeignete Schätzfunktion für die relative Häufigkeit der Personen in Deutschland, bei denen im letzten Jahr eine Angststörung diagnostiziert wurde.

      Der Mittelwert von Bernoulli-Variablen entspricht der relativen Häufigkeit. Ein geeigneter Schätzer für die relative Häufigkeit für die Variable Angststörung in Deutschland wäre daher:

      \[\overline{X} = \frac{1}{n}\sum_{i = 1}^{n}X_{i}\]

    2. Geben Sie den Erwartungswert und den Standardfehler dieser Schätzfunktion an und beurteilen Sie die Schätzfunktion anhand der Gütekriterien.

      \[E\left( \overline{X} \right) = \pi\]

      \[SE\left( \overline{X} \right) = \sqrt{\frac{\pi(1 - \pi)}{n}} = \sqrt{\frac{\pi(1 - \pi)}{500}}\]

      Die Schätzfunktion \(\overline{X}\) ist erwartungstreu, effizient und konsistent.

    3. Bei 38 Personen in Ihrer Stichprobe wurde im letzten Jahr eine Angststörung diagnostiziert. Bestimmen Sie den Schätzwert und interpretieren Sie ihn.

      \[\overline{x} = h(1) = \frac{38}{500} = 0,076\]

      Auf Basis der Stichprobe wird der Anteil Deutscher, bei denen im letzten Jahr eine Angststörung diagnostiziert wurde, auf 7.6 % geschätzt.

    4. Geben Sie den Standardfehler der Schätzfunktion für den Fall an, dass der Stichprobenumfang n = 1000 ist. Vergleichen Sie diesen mit dem in Teilaufgabe b bestimmten Standardfehler.

      \[SE\left( \overline{X} \right) = \sqrt{\frac{\pi(1 - \pi)}{n}} = \sqrt{\frac{\pi(1 - \pi)}{1000}}\]

      Der Standardfehler ist im Fall der größeren Stichprobe n = 1000 kleiner, da \(\pi\) gleich bleibt, aber das n im Nenner größer wird.