pnorm(169, 170, sqrt(1))[1] 0.1586553pnorm(171, 170, sqrt(1))[1] 0.8413447Übungsblatt 07
Parameterschätzung
Verbessern Sie in den folgenden Aussagen fehlerhafte Notationen:
Als Schätzwert für den Parameter \(\mu\) eignet sich der Mittelwert \(\bar{X}\) in der Stichprobe.
LösungAls Schätzwert für den Parameter \(\mu\) eignet sich der Mittelwert \(\bar{\mathbf{x}}\) in der Stichprobe.
Die Schätzfunktion\({\ \widehat{\sigma}}^{2} = s^{2}\) hat sich in dem Schätzwert \(S^{2}\) realisiert.
LösungDie Schätzfunktion \({{\widehat{\sigma}}^{2} = \mathbf{S}}^{\mathbf{2}}\) hat sich in dem Schätzwert \(\mathbf{s}^{\mathbf{2}}\) realisiert.
\({\widehat{\sigma}}_{Wert}^{2} = S^{2}\) ist eine erwartungstreue Schätzfunktion für den Parameter\({\ \widehat{\sigma}}^{2}\).
Lösung\({\mathbf{\ }\widehat{\mathbf{\sigma}}}^{\mathbf{2}} = S^{2}\) ist eine erwartungstreue Schätzfunktion für den Parameter\(\mathbf{\ \sigma}^{\mathbf{2}}\).
Der Wert des Parameters \(\widehat{\pi}\) bestimmt die genaue Form der Wahrscheinlichkeitsfunktion der Bernoulli-Verteilung.
LösungDer Wert des Parameters \(\pi\) bestimmt die genaue Form der Wahrscheinlichkeitsfunktion der Bernoulli-Verteilung.
Eine Schätzfunktion \(\widehat{\theta}\) ist erwartungstreu für einen Parameter \(\theta\), falls \(E\left( {\widehat{\theta}}_{Wert} \right) = \theta\).
LösungEine Schätzfunktion \(\widehat{\theta}\) ist erwartungstreu für einen Parameter \(\theta\), falls \(E\left( \widehat{\mathbf{\theta}} \right) = \theta\).
Der Standardfehler der Schätzfunktion \(\widehat{\mu} = \bar{X}\) ist \(SE\left( \bar{x} \right) = \sqrt{\frac{{\widehat{\sigma}}_{Wert}^{2}}{n}}\).
LösungDer Standardfehler der Schätzfunktion \(\widehat{\mu} = \bar{X}\) ist \(SE\left( \bar{\mathbf{X}} \right) = \sqrt{\frac{\mathbf{\ \sigma}^{\mathbf{2}}}{n}}\).
Ein zufälliges Intervall \(I\left( X_{1},\ X,\ \ldots,\ X \right) = \lbrack U,\ O\rbrack\) heißt Konfidenzintervall für einen Parameter \(\theta\) mit Konfidenzniveau \(1 - \alpha\), falls \(P(u \leq \theta \leq o) = 1 - \alpha\).
LösungEin zufälliges Intervall \(I\left( X_{1},\ X_{2},\ \ldots,\ X_{n} \right) = \lbrack U,\ O\rbrack\) heißt Konfidenzintervall für einen Parameter \(\theta\) mit Konfidenzniveau \(1 - \alpha\), falls \(P\left( \mathbf{U} \leq \theta \leq \mathbf{O} \right) = 1 - \alpha\).
Ein konkretes Konfidenzintervall für den Parameter \(\widehat{\mu}\) ist \[I\left( x_{1},\ x_{2},\ \ldots,\ x_{n} \right) = \left\lbrack \bar{X} - t_{1 - \frac{\alpha}{2}} \cdot \sqrt{\frac{s^{2}}{n}},\bar{X} + t_{1 - \frac{\alpha}{2}} \cdot \sqrt{\frac{s^{2}}{n}} \right\rbrack\]
LösungEin konkretes Konfidenzintervall für den Parameter \(\mathbf{\mu}\) ist \[I\left( x_{1},\ x_{2},\ \ldots,\ x_{n} \right) = \left\lbrack \bar{\mathbf{x}} - t_{1 - \frac{\alpha}{2}} \cdot \sqrt{\frac{s^{2}}{n}},\bar{\mathbf{x}} + t_{1 - \frac{\alpha}{2}} \cdot \sqrt{\frac{s^{2}}{n}} \right\rbrack\]
Erklären Sie jeweils die folgenden Größen und wie diese miteinander zusammenhängen. Gehen Sie von einer einfachen Zufallsstichprobe mit \(X_{i}\ \sim\ N\left( \mu,\ \ \sigma^{2} \right)\) aus.
\(E\left( X_{i} \right),\ E\left( \bar{X} \right)\), und \(\mu\)
Lösung\(E\left( X_{i} \right)\ \)ist der Erwartungswert der Zufallsvariable \(X_{i}\) und\(\ E\left( \bar{X} \right)\ \)ist der Erwartungswert der Schätzfunktion \(\bar{X}\). Beide Erwartungswerte entsprechen dem Parameter \(\mu\).
\(SD\left( X_{i} \right)\), \(SD\left( \bar{X} \right)\), \(SE\left( \bar{X} \right)\)
Lösung\(SD\left( X_{i} \right)\ \)ist die Standardabweichung der Zufallsvariable \(X_{i}\) und\(\ SD\left( \bar{X} \right)\ \)ist die Standardabweichung der Schätzfunktion \(\bar{X}\). \(SE\left( \bar{X} \right)\) ist der Standardfehler der Schätzfunktion \(\bar{X}\) und entspricht \(SD\left( \bar{X} \right)\). \(SD\left( X_{i} \right) = \sqrt{{\ \sigma}^{2}}\) und \(SE\left( \bar{X} \right) = SD\left( \bar{X} \right) = \sqrt{\frac{{\ \sigma}^{2}}{n}}\).
\(S^{2},S_{emp}^{2},s^{2},s_{emp}^{2},\ {\ \widehat{\sigma}}^{2},\ {\widehat{\sigma}}_{Wert}^{2},\ \ \)und\({\ \sigma}^{2}\)
Lösung\(S^{2}\)und \(S_{emp}^{2}\) sind Zufallsvariablen und \(s^{2}\)und \(s_{emp}^{2}\) jeweils deren Realisationen. \({\ \sigma}^{2}\) ist ein Parameter der Normalverteilung. \({\ \widehat{\sigma}}^{2}\) ist die Bezeichnung für eine allgemeine Schätzfunktion für den Parameter \({\ \sigma}^{2}\), deren Realisation ein allgemeiner Schätzwert \({\widehat{\sigma}}_{Wert}^{2}\) für \({\ \sigma}^{2}\) ist.
\(S^{2}\) und \(S_{emp}^{2}\) könnten beide als konkrete Schätzfunktionen für \({\ \sigma}^{2}\) verwendet werden, allerdings ist nur \(S^{2}\) auch erwartungstreu für \(\sigma^{2}\). Daher ist \(S^{2}\) eine bessere Schätzfunktion für \(\sigma^{2}\) als \(S_{emp}^{2}\). Möchte man die empirische Varianz in einer Stichprobe berechnen, so berechnet man \(s_{emp}^{2}\). Möchte man jedoch den Parameter \(\sigma^{2}\ \)schätzen, so berechnet man den Schätzwert\({\ s}^{2}\) in der Stichprobe.
Wir interessieren uns für die durchschnittliche Körpergröße (in cm) von PsychologiestudentInnen in Deutschland. Wir ziehen hierfür eine einfache Zufallsstichprobe der Größe n = 100. Die Zufallsvariablen \(X_{1},\ X_{2},\ \ldots,\ X_{i},\ldots,\ X_{n}\) stehen jeweils für die Körpergröße der i-ten gezogenen Person. Wir nehmen an, dass \(X_{i}\ \sim\ N\left( \mu,\ \ \sigma^{2} \right)\) mit \(\mu = 170\) und \(\sigma^{2} = 100\) gilt. Als Schätzfunktion für \(\mu\) betrachten wir \(\widehat{\mu} = \bar{X}\).
Was ist (unter den oben genannten Annahmen) die durchschnittliche Körpergröße der PsychologiestudentInnen in Deutschland?
LösungDie durchschnittliche Körpergröße entspricht dem Parameter \(\mu\), ist also gleich 170cm.
Wie können Sie die Realisation \(x_{1}\) der Zufallsvariable \(X_{1}\) interpretieren?
LösungKörpergröße der ersten zufällig gezogenen Person.
Geben Sie die Standardabweichung von \(X_{1}\) an. Interpretieren Sie diese.
Lösung\[SD\left( X_{1} \right) = \sqrt{Var\left( X_{1} \right)} = \sqrt{\sigma^{2}} = \sqrt{100} = 10\]
Falls wir unendlich oft eine einfache Zufallsstichprobe der Größe n = 100 ziehen würden und jedes Mal nur die Körpergröße der ersten zufällig gezogenen Person betrachten würden, wäre die empirische Standardabweichung dieser Werte gleich 10.
Geben Sie die Wahrscheinlichkeitsverteilung \(P_{X_{1}}\) von \(X_{1}\) an.
Lösung\[X_{1}\ \sim\ N(170,\ 100)\]
Wie können Sie die Realisation \(\bar{x}\) der Schätzfunktion \(\bar{X}\) interpretieren (falls der Parameterwert von \(\mu\) unbekannt wäre)?
Lösung\(\bar{x}\) ist die durchschnittliche Körpergröße in der von uns gezogenen Stichprobe und gleichzeitig ein Schätzwert für \(\mu\).
Geben Sie die Standardabweichung der Schätzfunktion \(\bar{X}\) an. Interpretieren Sie diese.
Lösung\[SD\left( \bar{X} \right) = \sqrt{\frac{\sigma^{2}}{n}} = \sqrt{\frac{100}{100}} = \sqrt{1} = 1\]
\(SD\left( \bar{X} \right) = SE\left( \bar{X} \right)\) ist der Standardfehler der Schätzfunktion \(\bar{X}\). Interpretation: Falls wir unendlich oft eine einfache Zufallsstichprobe der Größe n = 100 ziehen würden und in jeder dieser Stichproben die durchschnittliche Körpergröße – also den Schätzwert für \(\mu\) - berechnen würden, wäre die empirische Standardabweichung dieser Schätzwerte gleich 1.
Geben Sie die Wahrscheinlichkeitsverteilung \(P_{\bar{X}}\) der Schätzfunktion \(\bar{X}\) an.
Lösung\[E\left( \bar{X} \right) = \mu = 170\]
\[Var\left( \bar{X} \right) = \frac{\sigma^{2}}{n} = \frac{100}{100} = 1\]
\[\bar{X}\ \sim\ N(170,\ 1)\]
Veranschaulichen Sie die Wahrscheinlichkeitsdichtefunktionen von \(X_{1}\) und \(\bar{X}\) jeweils graphisch (Hinweis: eine sehr grobe Skizze ist ausreichend).
Lösung
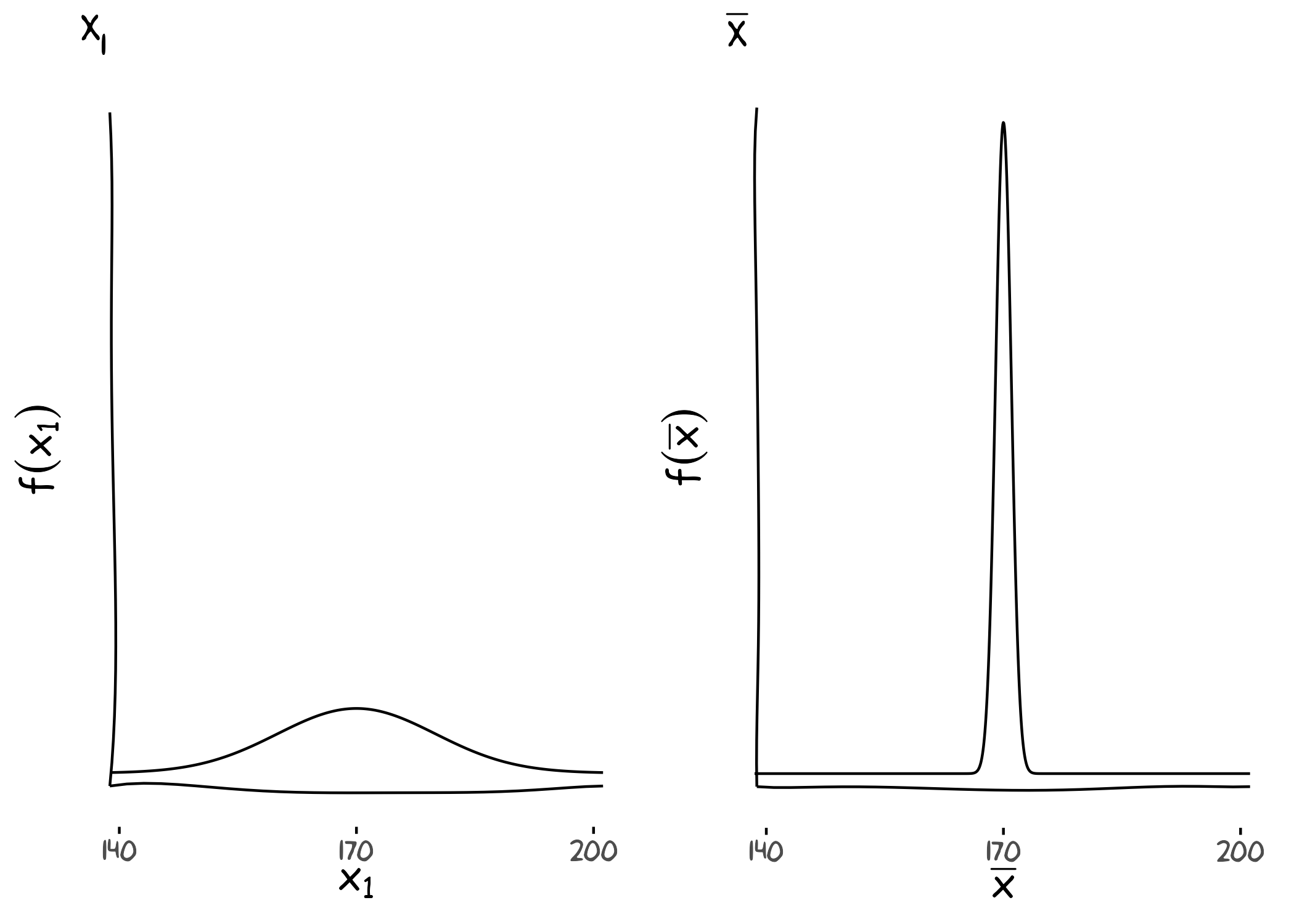
Berechnen Sie in R die Wahrscheinlichkeit dafür, dass sich die Schätzfunktion \(\bar{X}\) in einem Schätzwert realisiert, der weiter als 1 cm von dem wahren Parameterwert \(\mu = 170\) entfernt ist.
LösungDie Wahrscheinlichkeit dafür, dass sich die Schätzfunktion \(\bar{X}\) in einem Schätzwert realisiert, der weiter als 1 cm von dem wahren Parameterwert entfernt ist, ist die Wahrscheinlichkeit dafür, dass sie sich in einem Schätzwert realisiert, der kleiner als 169 oder größer als 171 ist.
\[P\left( \bar{X} < 169 \right) = P\left( \bar{X} \leq 169 \right) = F(169)\]
\[P\left( \bar{X} > 171 \right) = 1 - P\left( \bar{X} \leq 171 \right) = 1 - F(171)\]
Wir wissen, dass \(\bar{X}\ \sim\ N(170,\ 1)\) gilt, und können deshalb \(F(169)\) und \(F(171)\) mithilfe der Funktion pnorm in R berechnen:
Es ergibt sich
\[F(169) = 0.1586553\]
\[F(171) = 0.8413447\]
Und damit
\[ \begin{align*} P\left( \bar{X} < 169\ oder\ \bar{X} > 171 \right) &= P\left( \bar{X} < 169 \right) + P\left( \bar{X} > 171 \right) \\ &= F(169) + 1 - F(171) \\ &= 0.1586553 + 1 - 0.8413447 \approx 0.32 \end{align*} \]
Die Wahrscheinlichkeit dafür, dass sich die Schätzfunktion \(\bar{X}\) in einem Schätzwert realisiert, der weiter als 1 cm von dem wahren Parameterwert entfernt ist, beträgt also 32%.
Sei nun die Größe der Zufallsstichprobe n = 1000 statt n = 100. Welcher Wahrscheinlichkeitsverteilung folgt die Schätzfunktion \(\bar{X}\) in diesem Fall? Berechnen Sie die Wahrscheinlichkeit dafür, dass sich diese Schätzfunktion in einem Schätzwert realisiert, der weiter als 1 cm von dem wahren Parameterwert \(\mu = 170\) entfernt ist.
Lösung\[E\left( \bar{X} \right) = \mu = 170\]
\[Var\left( \bar{X} \right) = \frac{\sigma^{2}}{n} = \frac{100}{1000} = 0.1\]
\[\bar{X}\ \sim\ N(170,\ 0.1)\]
Die Wahrscheinlichkeit dafür, dass sich die Schätzfunktion \(\bar{X}\) in einem Schätzwert realisiert, der weiter als 1 cm von dem wahren Parameterwert entfernt ist, ist die Wahrscheinlichkeit dafür, dass sie sich in einem Schätzwert realisiert, der kleiner als 169 oder größer als 171 ist.
\[P\left( \bar{X} < 169 \right) = P\left( \bar{X} \leq 169 \right) = F(169)\]
\[P\left( \bar{X} > 171 \right) = 1 - P\left( \bar{X} \leq 171 \right) = 1 - F(171)\]
Wir wissen, dass \(\bar{X}\ \sim\ N(170,\ 0.1)\) gilt und können deshalb \(F(169)\) und \(F(171)\) mithilfe der Funktion pnorm in R berechnen:
pnorm(169, 170, sqrt(0.1))[1] 0.0007827011pnorm(171, 170, sqrt(0.1))[1] 0.9992173Es ergibt sich
\[F(169) = 0.0007827011\]
\[F(171) = 0.9992173\]
Und damit
\[ \begin{align*} P\left( \bar{X} < 169\ oder\ \bar{X} > 171 \right) &= P\left( \bar{X} < 169 \right) + P\left( \bar{X} > 171 \right) \\ &= F(169) + 1 - F(171) \\ &= 0.0007827011 + 1 - 0.9992173 \approx 0.002 \end{align*} \]
Die Wahrscheinlichkeit dafür, dass sich die Schätzfunktion \(\bar{X}\) bei einer Stichprobengröße von n = 1000 in einem Schätzwert realisiert, der weiter als 1 cm von dem wahren Parameterwert entfernt ist, beträgt also 0.2%.
Vergleichen Sie die Ergebnisse aus den Teilaufgaben i und j miteinander. Was fällt Ihnen auf?
LösungDie Wahrscheinlichkeit, dass sich der Schätzwert in einem Wert nahe dem wahren Wert des Parameters realisiert, ist in der größeren Stichprobe aus Teilaufgabe j größer. Der Grund dafür ist, dass aufgrund der Konsistenz der Schätzfunktion \(\bar{X}\) der Standardfehler immer kleiner wird, je größer die Stichprobe wird.