Übungsblatt 09
Unterschiede zwischen Populationen - Parameterschätzung
Sie interessieren sich für die durchschnittliche Religiösität von RepublikanerInnen und DemokratInnen und ziehen hierfür je eine Stichprobe aus der Population der RepublikanerInnen und aus der Population der DemokratInnen. Gehen Sie von folgender Ausgangssituation aus:
Stichprobe der RepublikanerInnen: \(X_{1i} \overset{\mathrm{iid}}{\sim}\ N\left( \mu_{1},\sigma^{2} \right)\) mit \(i = 1,\ 2,\ \ldots,\ n_{1}\)
Stichprobe der DemokratInnen: \(X_{2i} \overset{\mathrm{iid}}{\sim}\ N\left( \mu_{2},\sigma^{2} \right)\) mit \(i = 1,\ 2,\ \ldots,\ n_{2}\)
Welche Voraussetzungen müssen in den beiden Populationen und in Hinblick auf die Stichprobenziehung erfüllt sein, damit diese Ausgangssituation vorliegt?
TippLösungStichprobenziehung: Einfache Zufallsstichprobe aus der Population der RepublikanerInnen und einfache Zufallsstichprobe aus der Population der DemokratInnen.
Population: Die empirische Varianz der Religiösität in der Population der RepublikanerInnen ist genauso groß wie die empirische Varianz der Religiosität in der Population der DemokratInnen. Das Histogramm der Religiösität kann in beiden Populationen durch die Wahrscheinlichkeitsdichtefunktion einer Normalverteilung approximiert werden.
Welchen deskriptivstatistischen Größen in den Populationen entsprechen die Parameter \(\mu_{1}\), \(\mu_{2}\) und \(\sigma^{2}\) unter diesen Voraussetzungen jeweils?
TippLösung\(\mu_{1}\) entspricht der mittleren Religiösität in der Population der RepublikanerInnen.
\(\mu_{2}\) entspricht der mittleren Religiösität in der Population der DemokratInnen.
\(\sigma^{2}\) entspricht der empirischen Varianz der Religiösität sowohl in der Population der RepublikanerInnen als auch in der Population der DemokratInnen.
Wir betrachten die Zufallsvariable \(X_{14}\):
Wie können Sie die Realisation \(x_{14}\) von \(X_{14}\) interpretieren?
TippLösung\(x_{14}\) ist die Religiösität der vierten gezogenen Person aus der Population der RepublikanerInnen.
Geben Sie den Erwartungswert, die Varianz und die Standardabweichung von \(X_{14}\) an.
TippLösung\[E\left( X_{14} \right) = \mu_{1}\]
\[Var\left( X_{14} \right) = \sigma^{2}\]
\[SD\left( X_{14} \right) = \sqrt{\sigma^{2}}\]
Wir betrachten die Zufallsvariable \(X_{23}\):
Wie können Sie die Realisation \(x_{23}\) von \(X_{23}\) interpretieren?
TippLösung\(x_{23}\) ist die Religiösität der/des dritten gezogenen Demokraten/Demokratin.
Geben Sie den Erwartungswert, die Varianz und die Standardabweichung von \(X_{23}\) an.
TippLösung\[E\left( X_{23} \right) = \mu_{2}\]
\[Var\left( X_{23} \right) = \sigma^{2}\]
\[SD\left( X_{23} \right) = \sqrt{\sigma^{2}}\]
Wir betrachten die Zufallsvariable \({\overline{X}}_{1}\):
Wie können Sie die Realisation \({\overline{x}}_{1}\) von \({\overline{X}}_{1}\) interpretieren?
TippLösung\({\overline{x}}_{1}\) ist der Mittelwert der Religiösität in der Stichprobe der RepublikanerInnen.
Geben Sie den Erwartungswert, die Varianz und die Standardabweichung von \({\overline{X}}_{1}\) an.
TippLösung\[E\left( {\overline{X}}_{1} \right) = \mu_{1}\]
\[Var\left( {\overline{X}}_{1} \right) = \frac{\sigma^{2}}{n_{1}}\]
\[SD\left( {\overline{X}}_{1} \right) = \sqrt{\frac{\sigma^{2}}{n_{1}}}\]
Für welchen Parameter eignet sich \({\overline{X}}_{1}\) als Schätzfunktion?
TippLösung\({\overline{X}}_{1}\) eignet sich als Schätzfunktion für \(\mu_{1}\), also für den Mittelwert der Religiösität in der Population der RepublikanerInnen.
Wir betrachten die Zufallsvariable \({\overline{X}}_{2}\):
Wie können Sie die Realisation \({\overline{x}}_{2}\) von \({\overline{X}}_{2}\) interpretieren?
TippLösung\({\overline{x}}_{2}\) ist der Mittelwert der Religiösität in der Stichprobe der DemokratInnen.
Geben Sie den Erwartungswert, die Varianz und die Standardabweichung von \({\overline{X}}_{2}\) an.
TippLösung\[E\left( {\overline{X}}_{2} \right) = \mu_{2}\]
\[Var\left( {\overline{X}}_{2} \right) = \frac{\sigma^{2}}{n_{2}}\]
\[SD\left( {\overline{X}}_{2} \right) = \sqrt{\frac{\sigma^{2}}{n_{2}}}\]
Für welchen Parameter eignet sich \({\overline{X}}_{2}\) als Schätzfunktion?
TippLösung\({\overline{X}}_{2}\) eignet sich als Schätzfunktion für \(\mu_{2}\), also für den Mittelwert der Religiösität in der Population der DemokratInnen.
Wir betrachten die Zufallsvariable \({\overline{X}}_{Diff} = {\overline{X}}_{1} - {\overline{X}}_{2}\):
Wie können Sie die Realisation \({\overline{x}}_{Diff}\) von \({\overline{X}}_{Diff}\) interpretieren?
TippLösung\({\overline{x}}_{Diff}\) ist die Differenz zwischen dem Mittelwert der Religiösität in der Stichprobe der RepublikanerInnen und dem Mittelwert der Religiösität in der Stichprobe der DemokratInnen.
Geben Sie den Erwartungswert, die Varianz und die Standardabweichung von \({\overline{X}}_{Diff}\) an.
TippLösung\[E\left( {\overline{X}}_{Diff} \right) = \mu_{1} - \mu_{2}\]
\[Var\left( {\overline{X}}_{Diff} \right) = \frac{\sigma^{2}}{n_{1}} + \frac{\sigma^{2}}{n_{2}}\]
\[SD\left( {\overline{X}}_{Diff} \right) = \sqrt{\frac{\sigma^{2}}{n_{1}} + \frac{\sigma^{2}}{n_{2}}}\]
Für welchen Parameter eignet sich \({\overline{X}}_{Diff}\) als Schätzfunktion?
TippLösung\({\overline{X}}_{Diff}\) eignet sich als Schätzfunktion für \(\mu_{1} - \mu_{2}\), also für die Differenz zwischen dem Mittelwert der Religiösität in der Population der RepublikanerInnen und dem Mittelwert der Religiösität in der Population der DemokratInnen.
Wir betrachten die Zufallsvariable \(S_{pool}^{2}\):
Geben Sie den Erwartungswert von \(S_{pool}^{2}\) an.
TippLösung\[E\left( S_{pool}^{2} \right) = \sigma^{2}\]
Für welchen Parameter eignet sich \(S_{pool}^{2}\) als Schätzfunktion?
TippLösung\(S_{pool}^{2}\) eignet sich als Schätzfunktion für \(\sigma^{2}\), also für die empirische Varianz der Religiösität sowohl in der Population der RepublikanerInnen als auch in der Population der DemokratInnen.
Sie haben eine neue Form der Psychotherapie entwickelt und wollen herausfinden, welchen Einfluss diese auf die durchschnittliche Depressionsschwere von depressiven PatientInnen hat. Hierfür ziehen Sie eine einfache Zufallsstichprobe von vier depressiven PatientInnen und führen Ihre Psychotherapie mit diesen durch. Sie erfassen die (stetige) Depressionsschwere der PatientInnen vor und nach der Therapie:
PatientIn Depressionsschwere vor der Therapie Depressionsschwere nach der Therapie 1 7 1 2 3 2 3 4 2 4 1 1 Berechnen Sie ein 0.95-Konfidenzintervall für die Differenz der durchschnittlichen Depressionsschwere der PatientInnen vor und nach ihrer Therapie und interpretieren Sie dieses. Sie können davon ausgehen, dass alle Annahmen erfüllt sind. Verwenden Sie für die Berechnung des Quantils \(t_{1 - \frac{\alpha}{2}}\) die Funktion
qtin R.TippLösungAufgrund der Messwiederholung liegen abhängige Stichproben vor. Wir müssen also das konkrete Konfidenzintervall für \(\mu_{1} - \mu_{2}\) bei abhängigen Stichproben berechnen.
Formel:
\[I\left( x_{1},\ldots,x_{n} \right) = \left\lbrack {(\overline{x}}_{1} - {\overline{x}}_{2}) - t_{1 - \frac{\alpha}{2}} \cdot \sqrt{\frac{s_{Diff}^{2}}{n}},{(\overline{x}}_{1} - {\overline{x}}_{2}) + t_{1 - \frac{\alpha}{2}} \cdot \sqrt{\frac{s_{Diff}^{2}}{n}} \right\rbrack\]
Wir benötigen also \({\overline{x}}_{1}\), \({\overline{x}}_{2}\), \(s_{Diff}^{2}\), \(t_{1 - \frac{\alpha}{2}}\) und \(n\).
\(n\) entspricht der Anzahl an PatientInnen in der Stichprobe, daher ist \(n = 4\).
\({\overline{x}}_{1}\) ist der Mittelwert der Depressionsschwere vor der Therapie:
\[{\overline{x}}_{1} = \frac{7 + 3 + 4 + 1}{4} = 3.75\]
\({\overline{x}}_{2}\) ist der Mittelwert der Depressionsschwere nach der Therapie:
\[{\overline{x}}_{2} = \frac{1 + 2 + 2 + 1}{4} = 1.5\]
\(s_{Diff}^{2}\) ist die korrigierte empirische Varianz der Differenzen \(x_{i\ Diff} = x_{1i} - x_{2i}\), d.h. der Differenzen der PatientInnen in der Depressionsschwere vor und nach der Therapie:
\[x_{1\ Diff} = x_{11} - x_{21} = 7 - 1 = 6\]
\[x_{2\ Diff} = x_{12} - x_{22} = 3 - 2 = 1\]
\[x_{2\ Diff} = x_{13} - x_{23} = 4 - 2 = 2\]
\[x_{2\ Diff} = x_{14} - x_{24} = 1 - 1 = 0\]
Der Mittelwert dieser Differenzen ist:
\[{\overline{x}}_{Diff} = \frac{6 + 1 + 2 + 0}{4} = 2.25\]
Damit ist
\[s_{Diff}^{2} = \frac{1}{n - 1}\sum_{i = 1}^{n}{\left( x_{i\ Diff} - {\overline{x}}_{Diff} \right)^{2} =}\] \[= \frac{1}{4 - 1}\left\lbrack (6 - 2.25)^{2} + (1 - 2.25)^{2} + (2 - 2.25)^{2} + (0 - 2.25)^{2} \right\rbrack \approx 6.92\]
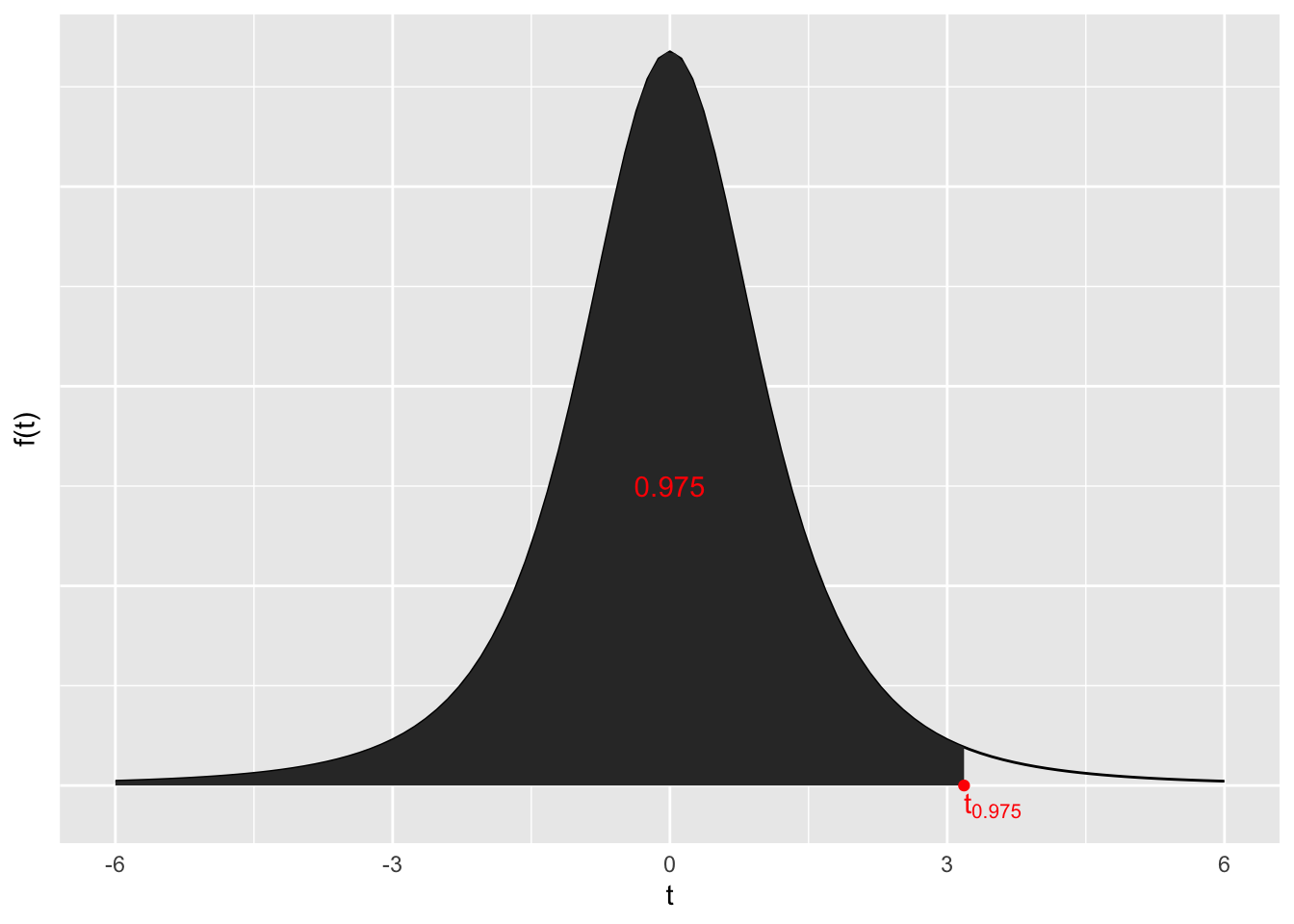
Da unser Konfidenzniveau \(1 - \alpha = 0.95\) sein soll, suchen wir \(t_{1 - \frac{\alpha}{2}} = t_{1 - \frac{0.05}{2}} = t_{0.975}\).
Dies ist der Wert für den unter einer t-Verteilung mit \(\nu = n - 1 = 4 - 1 = 3\) gilt, dass \(F\left( t_{0.975} \right) = 0.975\).
Graphische Veranschaulichung anhand der Wahrscheinlichkeitsdichtefunktion der t-Verteilung:
Graphische Veranschaulichung anhand der Verteilungsfunktion der t-Verteilung:
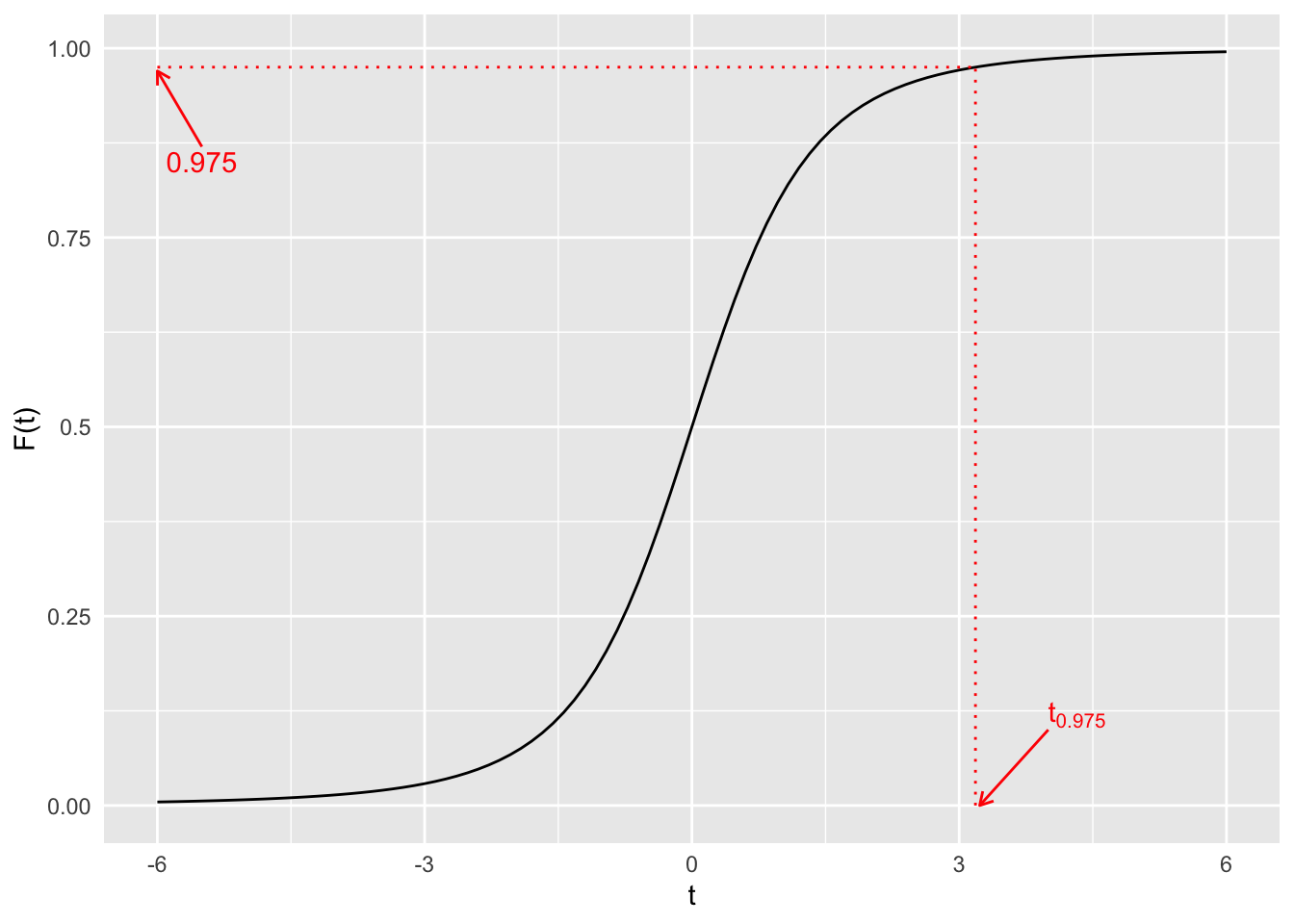
Berechnung von \(t_{0.975}\) in R:
qt(0.975, 3)[1] 3.182446Also ist \(t_{0.975} \approx 3.18\).
Nun können wir in die Formel für das konkrete KI einsetzen:
\[\begin{align*} I\left( x_{1},\ldots,x_{n} \right) &= \left\lbrack {(\overline{x}}_{1} - {\overline{x}}_{2}) - t_{1 - \frac{\alpha}{2}} \cdot \sqrt{\frac{s_{Diff}^{2}}{n}},{(\overline{x}}_{1} - {\overline{x}}_{2}) + t_{1 - \frac{\alpha}{2}} \cdot \sqrt{\frac{s_{Diff}^{2}}{n}} \right\rbrack \\ &= \left\lbrack (3.75 - 1.5) - 3.18 \cdot \sqrt{\frac{6.92}{4}},(3.75 - 1.5) + 3.18 \cdot \sqrt{\frac{6.92}{4}} \right\rbrack \\ &\approx \lbrack - 1.93,\ 6.43\rbrack \end{align*}\]
Die plausiblen Werte für \(\mu_{1} - \mu_{2}\) und somit für die Differenz der mittleren Depressionsschwere der PatientInnen vor und nach der Therapie in der Population liegen also zwischen -1.93 und 6.43. Es wären Verschlechterungen von 1.93 bis Verbesserungen von 6.43 in der mittleren Depressionsschwere plausibel.
Sie interessieren sich dafür, wie stark sich BWL- und Psychologie-StudentInnen in ihrem durchschnittlichen IQ unterscheiden. Sie ziehen hierfür eine einfache Zufallsstichprobe der Größe \(n_{1} = 4\) aus der Population der BWL-StudentInnen und eine einfache Zufallsstichprobe der Größe \(n_{2} = 5\) aus der Population der Psychologie-StudentInnen. Die von Ihnen gezogenen BWL-StudentInnen weisen jeweils IQ-Werte von 105, 103, 110 und 115 auf. Die von Ihnen gezogenen Psychologie-StudentInnen weisen jeweils IQ-Werte von 107, 101, 99, 111 und 105 auf. Berechnen Sie ein 0.90-Konfidenzintervall für die Differenz des durchschnittlichen IQ von BWL- und Psychologie-StudentInnen und interpretieren Sie dieses. Sie können davon ausgehen, dass alle Annahmen erfüllt sind. Verwenden Sie für die Berechung des Quantils \(t_{1 - \frac{\alpha}{2}}\) die Funktion
qtin R und veranschaulichen Sie die Lage des Quantils graphisch jeweils anhand der Wahrscheinlichkeitsdichtefunktion und der Verteilungsfunktion der t-Verteilung.TippLösungDa sich in der Stichprobe der BWL-StundentInnen und in der Stichprobe der Psychologie-StudentInnen unterschiedliche Personen befinden, liegen unabhängige Stichproben vor. Wir müssen also das konkrete Konfidenzintervall für \(\mu_{1} - \mu_{2}\) bei unabhängigen Stichproben berechnen.
Formel:
\(I\left( x_{1},\ldots,x_{n} \right) = \left\lbrack {(\overline{x}}_{1} - {\overline{x}}_{2}) - t_{1 - \frac{\alpha}{2}} \cdot \sqrt{\frac{s_{pool}^{2}}{n_{1}} + \frac{s_{pool}^{2}}{n_{2}}},{(\overline{x}}_{1} - {\overline{x}}_{2}) + t_{1 - \frac{\alpha}{2}} \cdot \sqrt{\frac{s_{pool}^{2}}{n_{1}} + \frac{s_{pool}^{2}}{n_{2}}} \right\rbrack\)
Wir benötigen also \({\overline{x}}_{1}\), \({\overline{x}}_{2}\), \(s_{pool}^{2}\), \(t_{1 - \frac{\alpha}{2}}\), \(n_{1}\) und \(n_{2}\).
\(n_{1}\) entspricht der Anzahl an Personen in der Stichprobe der BWL-StudentInnen, daher ist \(n_{1} = 4\).
\(n_{2}\) entspricht der Anzahl an Personen in der Stichprobe der Psychologie-StudentInnen, daher ist \(n_{2} = 5\).
\({\overline{x}}_{1}\) ist der Mittelwert der IQ-Werte der BWL-StudentInnen:
\[{\overline{x}}_{1} = \frac{105 + 103 + 110 + 115}{4} = 108.25\]
\({\overline{x}}_{2}\) ist der Mittelwert der IQ-Werte der Psychologie-StudentInnen:
\[{\overline{x}}_{2} = \frac{107 + 101 + 99 + 111 + 105\ }{5} = 104.6\]
\(s_{pool}^{2}\) können wir aus der Formel
\[s_{pool}^{2} = \frac{\left( n_{1} - 1 \right) \cdot s_{1}^{2} + \left( n_{2} - 1 \right) \cdot s_{2}^{2}}{n_{1} + n_{2} - 2}\] berechnen.
Hierfür benötigen wir \(s_{1}^{2}\) und \(s_{2}^{2}\).
\(s_{1}^{2}\) ist die korrigierte empirische Varianz in der Stichprobe der BWL-StudentInnen:
\[s_{1}^{2} = \frac{1}{n_{1} - 1}\sum_{i = 1}^{n_{1}}\left( x_{1i} - {\overline{x}}_{1} \right)^{2} =\]
\[= \frac{1}{4 - 1}\left\lbrack (105 - 108.25)^{2} + (103 - 108.25)^{2} + (110 - 108.25)^{2} + (115 - 108.25)^{2} \right\rbrack \approx\]
\[\approx 28.92\]
\(s_{2}^{2}\) ist die korrigierte empirische Varianz in der Stichprobe der Psychologie-StudentInnen:
\[s_{2}^{2} = \frac{1}{n_{2} - 1}\sum_{i = 1}^{n_{2}}\left( x_{2i} - {\overline{x}}_{2} \right)^{2} =\]
\[= \frac{1}{5 - 1}\left\lbrack (107 - 104.6)^{2} + (101 - 104.6)^{2} + (99 - 104.6)^{2} + (111 - 104.6)^{2} + (105 - 104.6)^{2} \right\rbrack =\]
\[= 22.8\]
Einsetzen in die Formel für \(s_{pool}^{2}\):
\[s_{pool}^{2} = \frac{\left( n_{1} - 1 \right) \cdot s_{1}^{2} + \left( n_{2} - 1 \right) \cdot s_{2}^{2}}{n_{1} + n_{2} - 2} = \frac{(4 - 1) \cdot 28.92 + (5 - 1) \cdot 22.8}{4 + 5 - 2} \approx 25.42\]
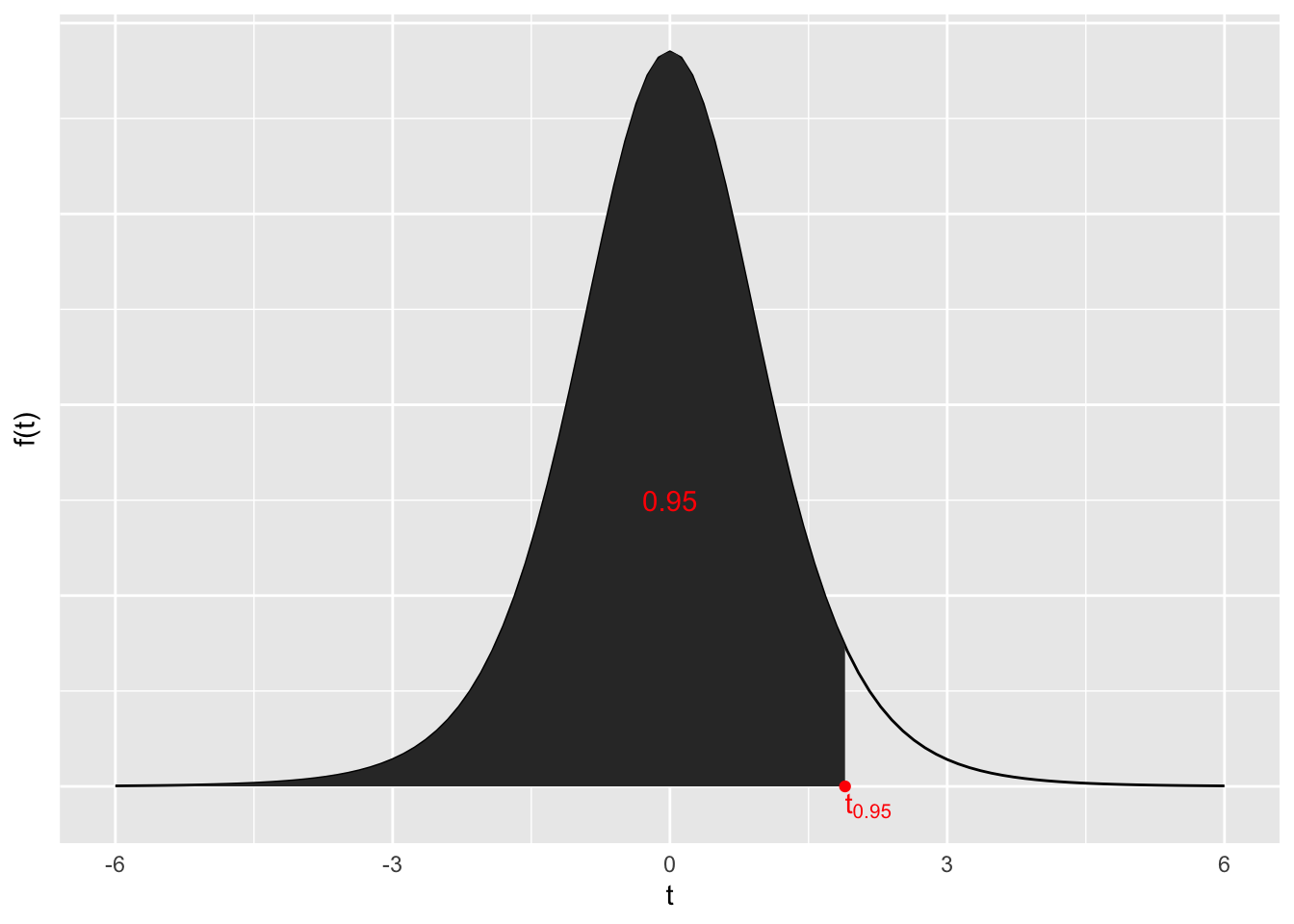
Da unser Konfidenzniveau \(1 - \alpha = 0.90\) sein soll, suchen wir \(t_{1 - \frac{\alpha}{2}} = t_{1 - \frac{0.1}{2}} = t_{0.95}\).
Dies ist der Wert für den unter einer t-Verteilung mit \(\nu = n_{1} + n_{2} - 2 = 4 + 5 - 2 = 7\) gilt, dass \(F\left( t_{0.95} \right) = 0.95\).
Graphische Veranschaulichung anhand der Wahrscheinlichkeitsdichtefunktion der t-Verteilung:
Graphische Veranschaulichung anhand der Verteilungsfunktion der t-Verteilung:
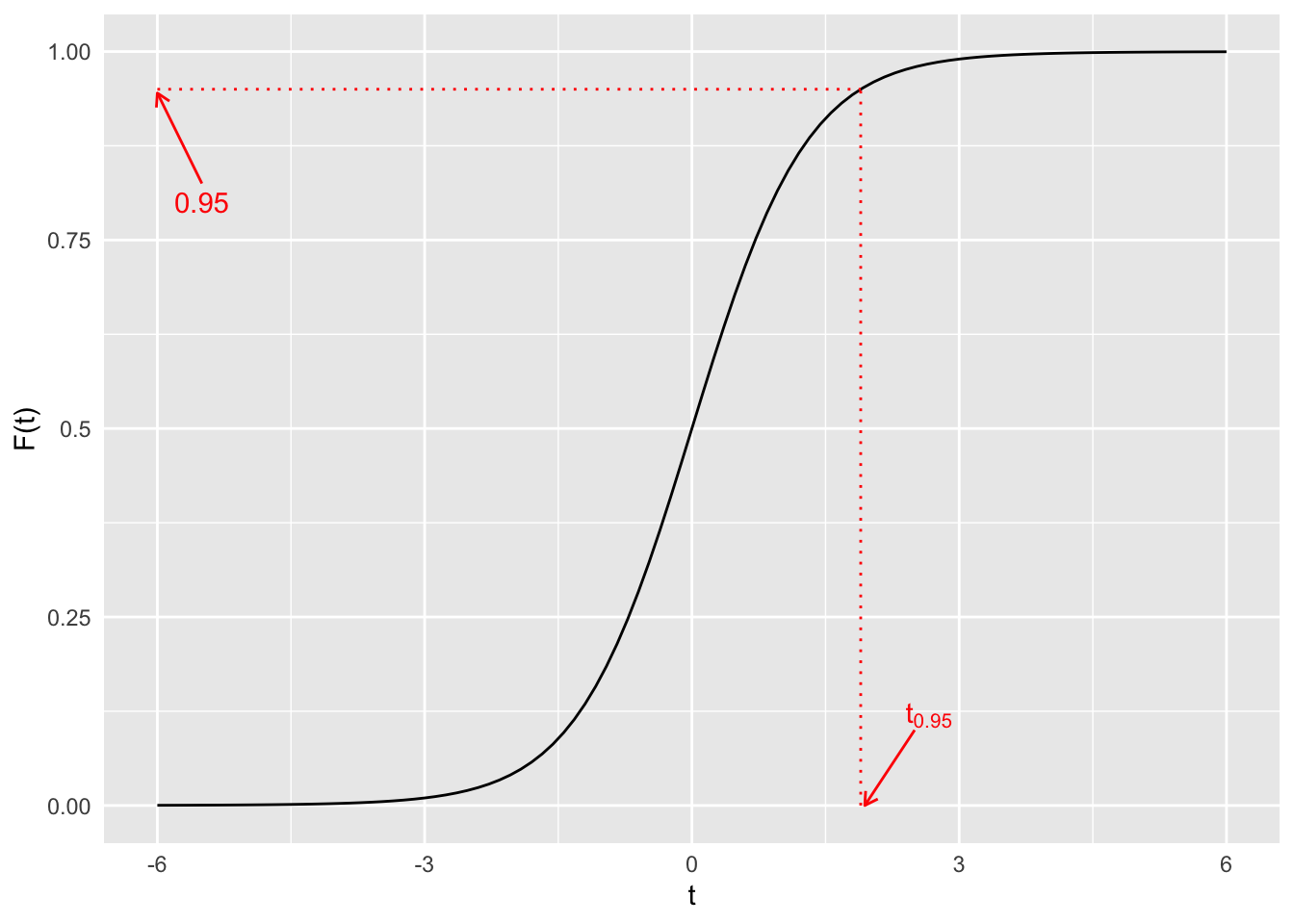
Berechnung von \(t_{0.95}\) in R:
qt(0.95, 7)[1] 1.894579Also ist \(t_{0.95} \approx 1.89\).
Nun können wir in die Formel für das konkrete KI einsetzen:
\(I\left( x_{1},\ldots,x_{n} \right) = \left\lbrack {(\overline{x}}_{1} - {\overline{x}}_{2}) - t_{1 - \frac{\alpha}{2}} \cdot \sqrt{\frac{s_{pool}^{2}}{n_{1}} + \frac{s_{pool}^{2}}{n_{2}}},{(\overline{x}}_{1} - {\overline{x}}_{2}) + t_{1 - \frac{\alpha}{2}} \cdot \sqrt{\frac{s_{pool}^{2}}{n_{1}} + \frac{s_{pool}^{2}}{n_{2}}} \right\rbrack =\)
\[= \left\lbrack (108.25 - 104.6) - 1.89 \cdot \sqrt{\frac{25.42}{4} + \frac{25.42}{5}},(108.25 - 104.6) + 1.89 \cdot \sqrt{\frac{25.42}{4} + \frac{25.42}{5}} \right\rbrack =\]
\[\approx \lbrack - 2.74,\ 10.04\rbrack\]
Die plausiblen Werte für \(\mu_{1} - \mu_{2}\) und somit für die Differenz des mittleren IQ von BWL-StudentInnen und Psychologie-StudentInnen in der Population liegen also zwischen -2.74 und 10.04. Es wäre also plausibel anzunehmen, dass BWL-StudentInnen in der Population im Mittel 2.74 IQ-Punkte weniger bis 10.04 IQ-Punkt mehr als Psychologie-StudentInnen aufweisen.
Sie interessieren sich für den Unterschied in der durchschnittlichen Nervosität von SchülerInnen vor und nach einem Referat. Laden Sie den Datensatz herunter, der Nervositäts-Messwerte einer einfachen Zufallsstichprobe von 200 SchülerInnen vor und nach einem Referat enthält. Berechnen Sie ein 0.95-Konfidenzintervall für die Differenz der durchschnittlichen Nervosität vor und nach dem Referat in R und interpretieren Sie dieses. Sie können davon ausgehen, dass alle Annahmen erfüllt sind.
HinweisHinweisCode für ein KI für \(\mu_{1} - \mu_{2}\) bei unabhängigen Stichproben:
t.test(MesswerteStichprobe1, MesswerteStichprobe2, paired = FALSE, var.equal = TRUE, conf.level = gewünschtes Konfidenzniveau)Code für ein KI für \(\mu_{1} - \mu_{2}\) bei abhängigen Stichproben:
t.test(MesswerteStichprobe1, MesswerteStichprobe2, paired = TRUE, conf.level = gewünschtes Konfidenzniveau)TippLösungAufgrund der Messwiederholung liegen abhängige Stichproben vor. Wir müssen also das konkrete Konfidenzintervall für \(\mu_{1} - \mu_{2}\) bei abhängigen Stichproben berechnen.
daten_ref <- read.csv2('referat.csv') t.test(daten_ref$NervDavor, daten_ref$NervDanach, paired=TRUE, conf.level=0.95)Paired t-test data: daten_ref$NervDavor and daten_ref$NervDanach t = 5.5934, df = 199, p-value = 7.294e-08 alternative hypothesis: true mean difference is not equal to 0 95 percent confidence interval: 5.218422 10.901578 sample estimates: mean difference 8.06Als 0.95-Konfidenzintervall ergibt sich:
\[I\left( x_{1},\ldots,x_{n} \right) \approx \lbrack 5.22,\ 10.90\rbrack\] Die plausiblen Werte für \(\mu_{1} - \mu_{2}\) und somit für die Differenz der mittleren Nervosität der SchülerInnen vor und nach dem Referat in der Population liegen also zwischen 5.22 und 10.90. Es wäre also in der Population der SchülerInnen ein Absinken der mittleren Nervosität um 5.22 bis 10.90 nach dem Referat plausibel.
Sie interessieren sich dafür, inwiefern sich PatientInnen mit Depression und PatientInnen mit Angststörung in ihrer durchschnittlichen Reaktionszeit (ms) auf einen Stimulus unterscheiden. Laden Sie den Datensatz herunter, der Reaktionszeiten einer einfachen Zufallsstichprobe von PatientInnen mit Depression und einer einfachen Zufallsstichprobe von PatientInnen mit Angsstörung enthält. Berechnen Sie ein 0.95-Konfidenzintervall für die Differenz der mittleren Reaktionszeit in R und interpretieren Sie dieses. Sie können davon ausgehen, dass alle Annahmen erfüllt sind.
HinweisHinweisVerwenden Sie in R die Indizierung mit eckigen Klammern
[], um je einen Datensatz für PatientInnen mit Depression und für PatientInnen mit Angststörung zu erstellen.TippLösungDa sich in der Stichprobe der PatientInnen mit Depression und in der Stichprobe der PatientInnen mit Angststörung unterschiedliche Personen befinden, liegen unabhängige Stichproben vor. Wir müssen also das konkrete Konfidenzintervall für \(\mu_{1} - \mu_{2}\) bei unabhängigen Stichproben berechnen.
daten_rt <- read.csv2('reaktionszeit.csv') Depression <- daten_rt[daten_rt$Diagnose == "Depression", ] Angststörung <- daten_rt[daten_rt$Diagnose == "Angst", ] t.test(Depression$RT, Angststörung$RT, paired=FALSE, var.equal=TRUE, conf.level=0.95)Two Sample t-test data: Depression$RT and Angststörung$RT t = 34.301, df = 498, p-value < 2.2e-16 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: 28.80772 32.30841 sample estimates: mean of x mean of y 229.7648 199.2067Als 0.95-Konfidenzintervall ergibt sich:
\[I\left( x_{1},\ldots,x_{n} \right) \approx \lbrack 28.81,\ 32.31\rbrack\]
Die plausiblen Werte für \(\mu_{1} - \mu_{2}\) und somit für die Differenz der mittleren Reaktionszeit von PatientInnen mit Depression und PatientInnen mit Angststörung in der Population liegen also zwischen \(28.81\) und \(32.31\) ms. Es wäre also plausibel anzunehmen, dass PatientInnen mit Depression in der Population im Mittel um \(28.81\) bis \(32.31\) Millisekunden langsamer reagieren als PatientInnen mit Angststörung.
Achten Sie auf die Reihenfolge, in der Sie der t.test Funktion die Vektoren mit den Messwerten der beiden Stichproben übergeben:
Zum Beispiel berechnet
t.test(daten_ref$NervDavor, daten_ref$NervDanach, paired=TRUE, conf.level=0.95)
in Aufgabe 4 das Konfidenzintervall für \(\mu_{davor} - \mu_{danach}\).
t.test(daten_ref$NervDanach, daten_ref$NervDavor, paired=TRUE, conf.level=0.95)
berechnet hingegen das Konfidenzintervall für \(\mu_{danach} - \mu_{davor}\).