Übungsblatt 1

Zusammengesetzte Hypothesentests

  1. Sie untersuchen die (stetige) Extraversion von Studierenden der drei Fächer Psychologie, Chemie und Physik in Deutschland. Sie vermuten, dass im Fach Psychologie die durchschnittliche Extraversion in der Population höher ist als in mindestens einem der beiden naturwissenschaftlichen Fächer.

    1. Stellen Sie die einzelnen statistischen Hypothesen auf.

      \[H_{01}:\ \mu_{Psy} - \mu_{Che} \leq 0\] \[H_{11}:\ \mu_{Psy} - \mu_{Che} > 0\]

      \[H_{02}:\ \mu_{Psy} - \mu_{Phy} \leq 0\] \[H_{12}:\ \mu_{Psy} - \mu_{Phy} > 0\]

    2. Stellen Sie die zusammengesetzten statistischen Hypothesen auf.

      \[H_{0}:\ \mu_{Psy} - \mu_{Che} \leq 0\ und\ \mu_{Psy} - \mu_{Phy} \leq 0\] \[H_{1}:\ \mu_{Psy} - \mu_{Che} > 0\ oder\ \mu_{Psy} - \mu_{Phy} > 0\]

    3. Lesen Sie den Datensatz in R ein und führen Sie die Hypothesentests für die einzelnen statistischen Hypothesen durch. Geben Sie die unkorrigierten p-Werte der einzelnen Hypothesentests an.

      # Extraversionsdaten einlesen
Daten <- read.csv2("Extraversion.csv")
      # Einzelne T-Tests für unabhaengige Stichproben durchfuehren
t1 <- t.test(Daten[Daten$Fach == "Psychologie", "Extraversion"], 
             Daten[Daten$Fach == "Chemie", "Extraversion"],
             alternative = "greater", var.equal = TRUE, paired = FALSE)
t1
      
 Two Sample t-test

data:  Daten[Daten$Fach == "Psychologie", "Extraversion"] and Daten[Daten$Fach == "Chemie", "Extraversion"]
t = 0.53342, df = 1010, p-value = 0.2969
alternative hypothesis: true difference in means is greater than 0
95 percent confidence interval:
 -0.07102686         Inf
sample estimates:
mean of x mean of y 
 100.0779  100.0438 
      t2 <- t.test(Daten[Daten$Fach == "Psychologie", "Extraversion"], 
             Daten[Daten$Fach == "Physik", "Extraversion"],
             alternative = "greater", var.equal = TRUE, paired = FALSE)
t2
      
 Two Sample t-test

data:  Daten[Daten$Fach == "Psychologie", "Extraversion"] and Daten[Daten$Fach == "Physik", "Extraversion"]
t = 2.602, df = 1142, p-value = 0.004694
alternative hypothesis: true difference in means is greater than 0
95 percent confidence interval:
 0.2024425       Inf
sample estimates:
mean of x mean of y 
100.07786  99.52674 
      # Unkorrigierte p-Werte abspeichern
p_unkorrigiert <- c(t1$p.value, t2$p.value)
p_unkorrigiert
      [1] 0.296931092 0.004694488

      \[p_{1} = 0.2969\] \[p_{2} = 0.0047\]

    4. Begründen Sie die Testentscheidung für die zusammengesetzten Hypothesen bei einem Signifikanzniveau von \(0.005\) und interpretieren Sie das Ergebnis. Falls Sie glauben, dass eine Korrektur notwendig ist, korrigieren Sie die p-Werte der einzelnen Hypothesentests mit der Bonferroni Methode anhand der Funktion p.adjust().

      Korrektur notwendig, da „oder”-Verknüpfung in der zusammengesetzten \(H_{1}.\)

      # Berechnung der Bonferroni korrigierten p-Werte
p_korrigiert <- p.adjust(p_unkorrigiert, method = "bonferroni")
p_korrigiert
      [1] 0.593862184 0.009388976

      \[p_{1\_ Bonferroni} = 0.5939 (= 0.2969 \cdot 2)\] \[p_{2\_ Bonferroni} = 0.0094 (= 0.0047 \cdot 2)\]

      Keiner der beiden korrigierten p-Werte ist kleiner als 0.005. Damit entscheiden wir uns für die zusammengesetzte Nullhypothese, dass in beiden naturwissenschaftlichen Fächern die durchschnittliche Extraversion in der Population mindestens genauso hoch ist wie im Fach Psychologie.

    5. Begründen Sie, warum es in dem vorliegenden Beispiel besonders wichtig ist, dass aus den drei Studienfächern große einfache Zufallsstichproben gezogen wurden. (Hinweis: Überprüfen Sie deskriptiv die statistischen Annahmen der einzelnen Hypothesentests).

      # Ueberpruefe die Annahmen der t-Tests
# Normalverteilung
hist(Daten[Daten$Fach == "Psychologie", "Extraversion"])

      hist(Daten[Daten$Fach == "Chemie", "Extraversion"])

      hist(Daten[Daten$Fach == "Physik", "Extraversion"])

      # Varianzgleichheit
var(Daten[Daten$Fach == "Psychologie", "Extraversion"])
      [1] 1.05658
      var(Daten[Daten$Fach == "Chemie", "Extraversion"])
      [1] 0.9882473
      var(Daten[Daten$Fach == "Physik", "Extraversion"])
      [1] 23.40408

      Die Varianz der Extraversion fällt in den drei Stichproben stark unterschiedlich aus, so dass man vermuten könnte, dass sich die Varianzen in den drei Populationen voneinander unterschieden. Damit wäre die Annahme der Varianzgleichheit der einzelnen t-Tests verletzt. Bei großen Stichproben, wie im vorliegenden Beispiel, kann man sich sicher sein, dass das vorgegebene Signifikanzniveau aufgrund des zentralen Grenzwertsatzes zumindest approximativ gilt. Anstatt sich auf den zentralen Grenzwertsatz zu verlassen, könnte man für die einzelnen Hypothesentests auch den Welch-Test (var.equal = FALSE) verwenden, der nicht annimmt, dass die Varianzen in der Population gleich sind.

  2. Sie untersuchen die (stetige) Depressionsschwere von 200 ambulant behandelten Depressiven in Deutschland zu drei Zeitpunkten: Einmal vor dem Beginn einer kognitiven Verhaltenstherapie (T1), einmal am Ende der Therapie (T2) und einmal 6 Monate nach dem Ende der Therapie (T3). Sie vermuten, dass die durchschnittliche Depressionsschwere in der Population vor der Therapie höher ist als am Ende der Therapie und dass die durchschnittliche Depressionsschwere am Ende der Therapie höher ist als 6 Monate nach der Therapie.

    1. Stellen Sie die einzelnen statistischen Hypothesen auf.

      \[H_{01}:\ \mu_{T1} - \mu_{T2} \leq 0\] \[H_{11}:\ \mu_{T1} - \mu_{T2} > 0\]

      \[H_{02}:\ \mu_{T2} - \mu_{T3} \leq 0\] \[H_{12}:\ \mu_{T2} - \mu_{T3} > 0\]

    2. Stellen Sie die zusammengesetzten statistischen Hypothesen auf.

      \[H_{0}:\ \mu_{T1} - \mu_{T2} \leq 0\ oder\ \mu_{T2} - \mu_{T3} \leq 0\] \[H_{1}:\ \mu_{T1} - \mu_{T2} > 0\ und\ \mu_{T2} - \mu_{T3} > 0\]

    3. Welche statistischen Hypothesentests verwenden Sie für die Überprüfung der Einzelhypothesen?

      Es werden zwei gerichtete t-Tests für abhängige Stichproben verwendet.

    4. Begründen Sie, ob das Signifikanzniveau für die einzelnen Hypothesentests korrigiert werden muss.

      Keine Korrektur, da „und”-Verknüpfung in der zusammengesetzten \(H_{1}.\)

  3. Sie wollen die folgenden zusammengesetzten Hypothesen überprüfen: \[H_{0}:\ H_{01}\ und\ H_{02}\ und\ H_{03}\] \[H_{1}:\ H_{11}\ oder\ H_{12}\ oder\ H_{13}\]

    1. Gehen Sie zunächst davon aus, dass die Hypothesentests zur Überprüfung der einzelnen Hypothesen unabhängig voneinander sind und jeweils ein Signifikanzniveau von \(\alpha = 0.005\) aufweisen. Wie groß wäre in diesem Fall das Signifikanzniveau \(\alpha^{*}\) des zusammengesetzten Hypothesentests?

      Wir haben drei einzelne Hypothesentests, daher ist \(N = 3\).

      \[\alpha^{*} = 1 - (1 - \alpha)^{N} = 1 - (1 - 0.005)^{3} = 1 - {0.995}^{3} \approx 0.015\]

    2. Berechnen Sie das Signifikanzniveau \(\alpha^{*}\) des zusammengesetzten Hypothesentests in R mithilfe der Wahrscheinlichkeitsfunktion der Binomialverteilung dbinom().

      \(\alpha^{*}\) entspricht in diesem Beispiel der Wahrscheinlichkeit, dass sich eine binomialverteilte Zufallsvariable mit Parametern n = 3 und \(\pi = \alpha = 0.005\) nicht in dem Wert 0 realisiert (d.h. bei mindestens einem der drei voneinander unabhängigen Hypothesentests entscheiden wir uns für die H1, obwohl die entsprechende H0 gilt)

      1 - dbinom(0, size = 3, prob = 0.005)
      [1] 0.01492512

    3. Wie groß müsste das Signifikanzniveau \(\alpha\) der einzelnen Tests sein, damit das Signifikanzniveau des zusammengesetzten Hypothesentests \(\alpha^{*} = 0.005\) ist?

      \[\alpha = 1 - \sqrt[N]{1 - \alpha^{*}} = 1 - \sqrt[3]{1 - 0.005} \approx 0.0017\]

    4. Gehen Sie nun davon aus, dass die Hypothesentests zur Überprüfung der einzelnen Hypothesen abhängig voneinander sind. Sie erhalten die folgenden p-Werte:

      \(p_{1} = 0.001\), \(p_{2} = 0.003\), \(p_{3} = 0.0005\)

      Berechnen Sie die Bonferroni-korrigierten Signifikanzniveaus für die einzelnen Tests, so dass das Signifikanzniveau für den zusammengesetzten Test höchstens \(\alpha^{*} = 0.005\) ist und treffen Sie eine Testentscheidung.

      \[\alpha = \frac{\alpha^{'}}{N} = \frac{0.005}{3} \approx 0.0017\]

      Da \(p_{1} < 0.0017\) und \(p_{3} < 0.0017\) ist, entscheiden wir uns für die zusammengesetzte Alternativhypothese.

    5. Berechnen Sie für den gleichen Fall die Bonferroni-korrigierten p-Werte per Hand und treffen Sie eine Testentscheidung für die zusammengesetzten Hypothesen auf der Basis der korrigierten p-Werte.

      \[p_{1\_ Bonferroni} = 0.001 \cdot 3 = 0.003\] \[p_{2\_ Bonferroni} = 0.003 \cdot 3 = 0.009\] \[p_{3\_ Bonferroni} = 0.0005 \cdot 3 = 0.0015\]

      Da \(p_{1\_ Bonferroni} < 0.005\) und \(p_{3\_ Bonferroni} < 0.005\) ist, entscheiden wir uns für die zusammengesetzte Alternativhypothese.

      (Hinweis: Dieses Vorgehen ist äquivalent zum Vorgehen aus der Teilaufgabe d. und kommt hinsichtlich der Testentscheidung immer zum gleichen Ergebnis.)

    6. Vergleichen Sie Ihr Ergebnis aus Teilaufgabe e. mit den Ergebnissen der R-Funktion p.adjust().

      p_werte <- c(0.001, 0.003, 0.0005)
p.adjust(p_werte, method = 'bonferroni')
      [1] 0.0030 0.0090 0.0015

  4. Sie wollen die folgenden zusammengesetzten Hypothesen überprüfen:

    \[H_{0}:\ H_{01}\ oder\ H_{02}\ oder\ H_{03}\]

    \[H_{1}:\ H_{11}\ und\ H_{12}\ und\ H_{13}\]

    1. Gehen Sie davon aus, dass die Hypothesentests zur Überprüfung der einzelnen Hypothesen unabhängig voneinander sind und jeweils ein Signifikanzniveau von \(\alpha = 0.005\) sowie eine Power von \(1 - \beta = 0.8\) aufweisen. Gehen Sie weiterhin davon aus, dass \(H_{01}\) falsch, \(H_{02}\) wahr und \(H_{03}\) falsch ist. Wie groß wäre in diesem Fall das Signifikanzniveau \(\alpha^{*}\) des zusammengesetzten Hypothesentests?

      Wir berechnen die Wahrscheinlichkeit, dass fälschlicherweise \(H_{02}\) und richtigerweise \(H_{01}\) sowie \(H_{03}\) abgelehnt werden:

      \[\alpha^{*} = {\alpha^{1} \cdot (1 - \beta)}^{2} = {0.005 \cdot (0.8)}^{2} = 0.0032\]

    2. Warum ist es in der Praxis, selbst für den einfachen Fall mit voneinander unabhängigen Hypothesentests, nicht einfach möglich, \(\alpha\) so festzulegen, dass \(\alpha^{*}\) exakt einem gewünschten Wert entspricht?

      In der Praxis ist die Basisrate, also welcher Anteil der getesteten Nullhypothesen tatsächlich wahr sind, unbekannt. Ebenfalls kennt man die tatsächliche Power der verwendeten Hypothesentests nicht. Da beide Größen sehr schwierig zu schätzen sind, wird in der Praxis bei zusammengesetzten Alternativhypothesen mit „und” normalerweise das Signifikanzniveau der einzelnen Hypothesentests nicht korrigiert, obwohl man zeigen kann, dass damit Power für die Prüfung der zusammengesetzten Hypothese „verschenkt” wird.

  5. Was ist ein Omnibustest und wann sollte ein solcher eingesetzt werden?

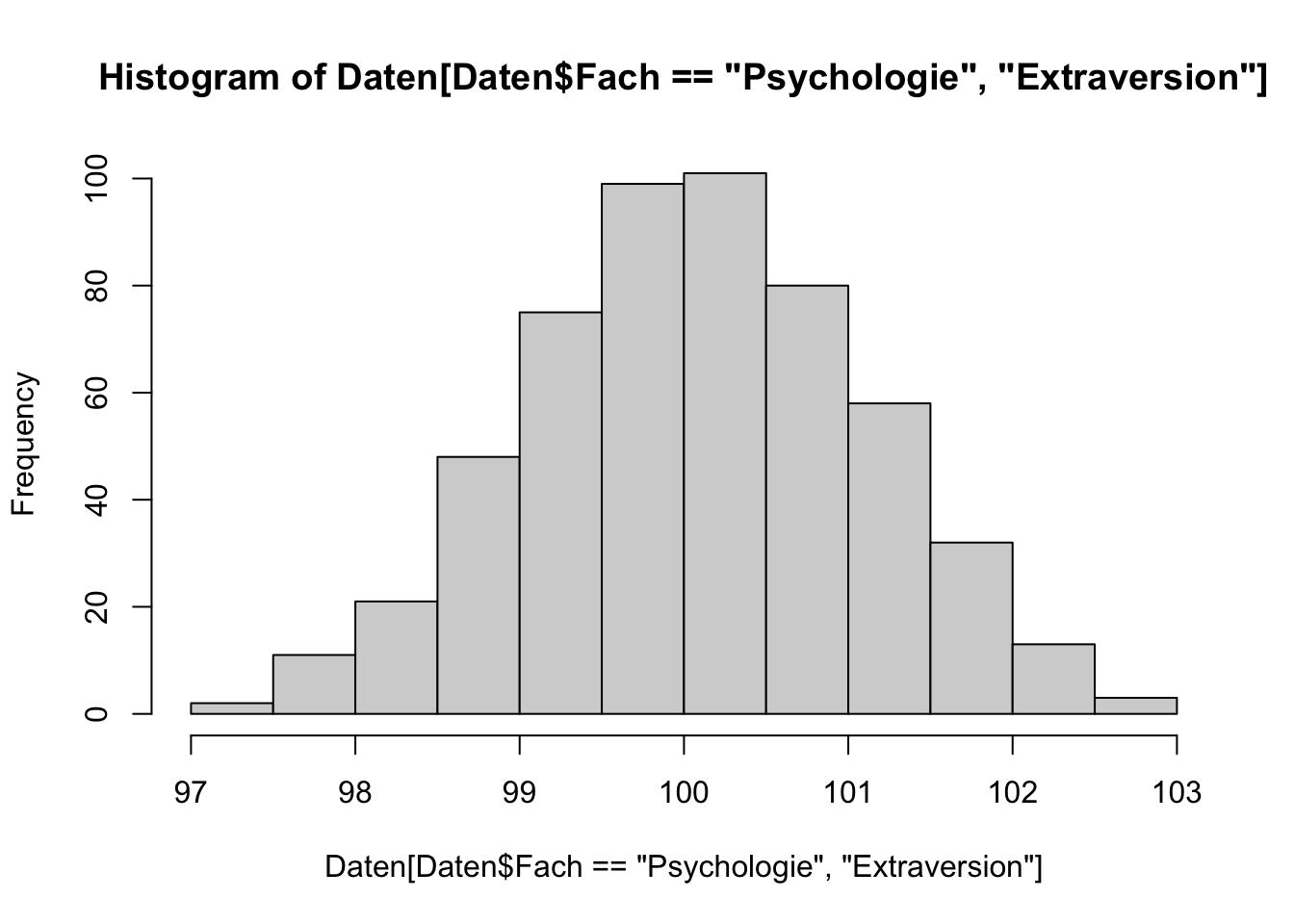
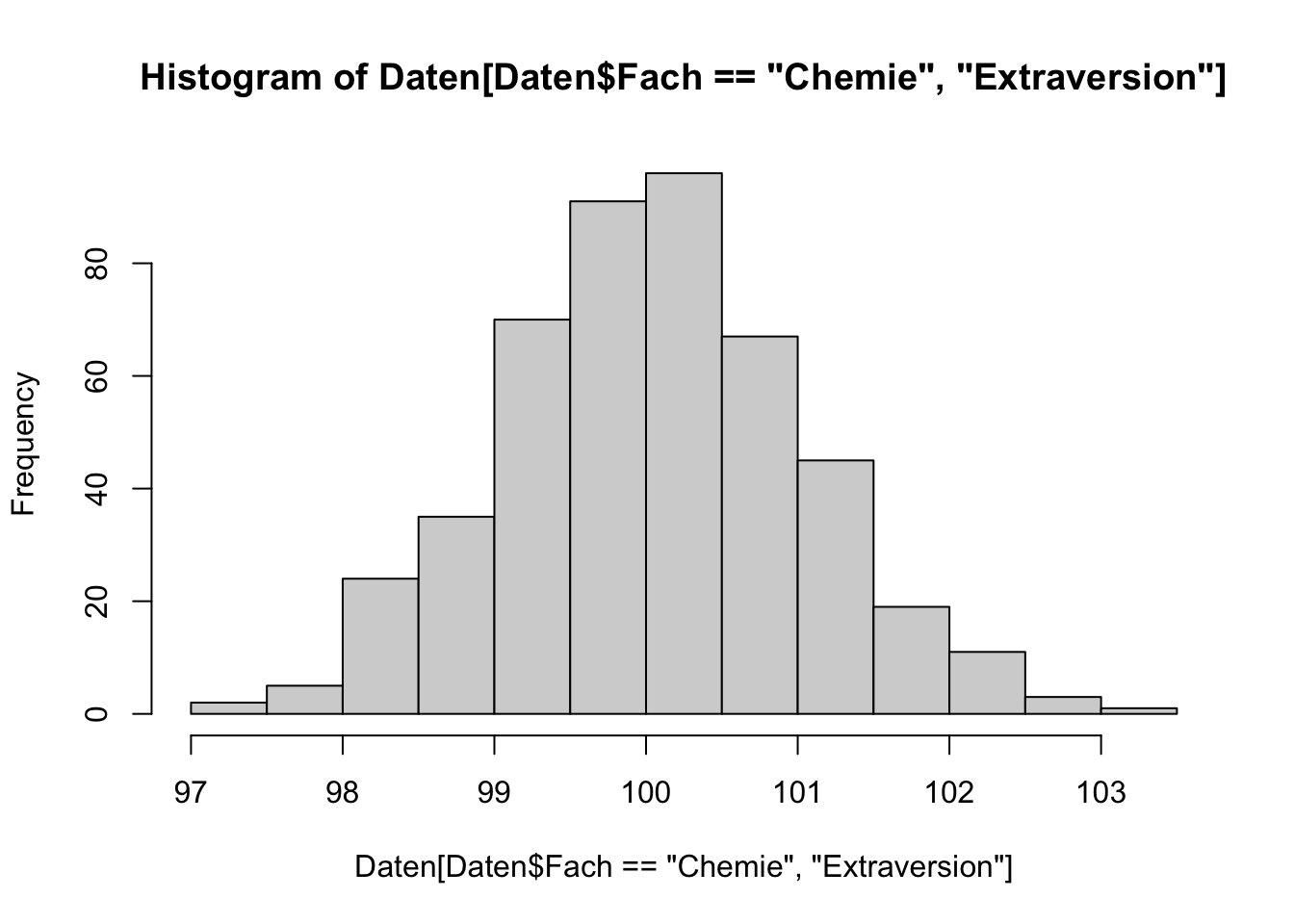
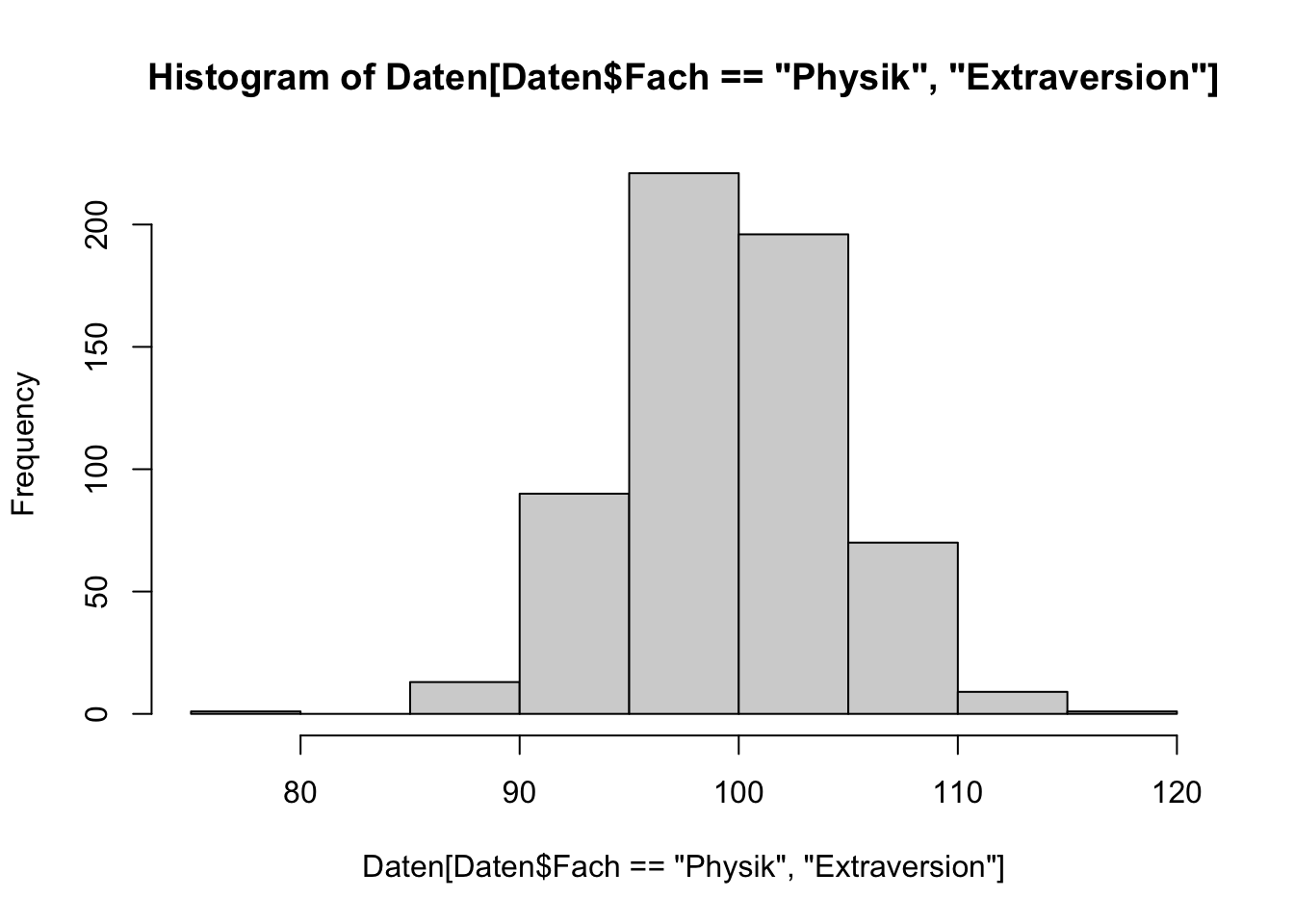
    Ein Omnibustest ist ein einziger statistischer Hypothesentest, zur Überprüfung einer zusammengesetzten statistischen Hypothese. Das heißt, es wird direkt die zusammengesetzte Hypothese und nicht die Einzelhypothesen überprüft. Wenn für die interessierende zusammengesetzte Hypothese ein passender Omnibustest bekannt ist, sollte dieser verwendet werden, da er typischerweise über eine höhere Power verfügt.

    Wir werden in den Vorlesungen zur Varianzanalyse und zur Regressionsanalyse solche Omnibustests kennen lernen. Für viele praktische Fragenstellungen, wie auch die Beispiele in den Aufgaben 1 und 2 in diesem Übungsblatt, existiert allerdings kein passender Omnibustest.

  6. Werden zusammengesetzte Alternativhypothesen anhand von Einzelhypothesen überprüft und muss eine Korrektur des Signifikanzniveaus der zusammengesetzten Alternativhypothese durchgeführt werden, haben wir drei Korrekturverfahren kennen gelernt: Sidak, Bonferroni, Tukey. Welche Methoden würden Sie welchen anderen Methoden vorziehen?

    Die Tukey Methode hat die größte Power, da sie die genaue Form der Abhängigkeiten zwischen den einzelnen Hypothesentests berücksichtigt und sollte daher immer präferiert werden, sofern sie im vorliegenden Fall angewendet werden kann. Die Tukey Methode ist allerdings nur in varianzanalytischen Modellen und Regressionsmodellen möglich, die wir erst in einigen Wochen besprechen werden. Wenn die Tukey Methode nicht eingesetzt werden kann, sollte die Bonferroni Methode der Sidak Methode vorgezogen werden, da die Sidak Methode nur bei voneinander unabhängigen einzelnen Hypothesentests funktioniert, was in der Praxis nur in den wenigsten Fällen gegeben ist.