# Stichprobengröße pro Experiment und pro Gruppe
n <- 10
# Der Seed stellt sicher, dass Sie die gleichen simulierten Daten erhalten
# wie in der Musterlösung
set.seed(21)
# Simuliere Datensätze der 5 Experimente
# x1: Konzentrationsleistung der Gruppe mit Präsentation emotional belastender Stimuli
# x2: Konzentrationsleistung der Kontrollgruppe
Daten1 <- data.frame(x1 = rnorm(n = n, mean = 0), x2 = rnorm(n = n, mean = 0))
Daten2 <- data.frame(x1 = rnorm(n = n, mean = 0), x2 = rnorm(n = n, mean = 0))
Daten3 <- data.frame(x1 = rnorm(n = n, mean = 0), x2 = rnorm(n = n, mean = 0))
Daten4 <- data.frame(x1 = rnorm(n = n, mean = 0), x2 = rnorm(n = n, mean = 0))
Daten5 <- data.frame(x1 = rnorm(n = n, mean = 0), x2 = rnorm(n = n, mean = 0))Übungsblatt 3
Publikationsbias, Researcher Degrees of Freedom und Open Science
Sie untersuchen in Ihrer Bachelorarbeit, ob die Präsentation von emotional belastenden Stimuli einen Einfluss auf die durchschnittliche Konzentrationsleistung von Studierenden hat. Da dieses Thema bisher noch wenig erforscht wurde und es dazu nicht viele Vorbefunde gibt, haben Sie sich zusammen mit Ihrer Betreuerin fünf verschiedene Experimente überlegt. In jedem Experiment wird ein anderer Typ von emotional belastenden Stimuli dargeboten, sowie jeweils ein anderer Konzentrationstest verwendet. Für jedes Experiment erheben Sie zwei einfache Zufallsstichproben mit n1 = n2 = 10. Dabei werden jeweils in der ersten Stichprobe während der Bearbeitung der Konzentrationsaufgabe emotional belastende Stimuli dargeboten und in der zweiten Stichprobe nicht.
Die Daten für dieses Übungsblatt finden Sie hier:
, , , ,Unten sehen Sie zur Orientierung das Skript, mit dem die Daten simuliert wurden. Beachten Sie hier für Ihre Erwartung bezüglich der Ergebnisse, aus welcher Verteilung die Werte beider Gruppen gezogen wurden. Sie müssen die Simulation nicht durchführen, sondern können gleich die fünf simulierten Datensätze herunterladen und einlesen.
HinweisSkript UB_3_Simulation.RTippDaten einlesenn <- 10 # Anzahl Personen pro Datensatz Daten1 <- read.csv2("Daten1.csv") Daten2 <- read.csv2("Daten2.csv") Daten3 <- read.csv2("Daten3.csv") Daten4 <- read.csv2("Daten4.csv") Daten5 <- read.csv2("Daten5.csv")Berechnen Sie ein kombiniertes metaanalytisches 95%-KI für \(\delta\).
TippLösung# Berechnung von Cohens d mit dem effsize Paket library(effsize) d1 <- cohen.d(Daten1$x1, Daten1$x2, na.rm = TRUE)$estimate d2 <- cohen.d(Daten2$x1, Daten2$x2, na.rm = TRUE)$estimate d3 <- cohen.d(Daten3$x1, Daten3$x2, na.rm = TRUE)$estimate d4 <- cohen.d(Daten4$x1, Daten4$x2, na.rm = TRUE)$estimate d5 <- cohen.d(Daten5$x1, Daten5$x2, na.rm = TRUE)$estimate ds <- c(d1, d2, d3, d4, d5) # Berechnung der Gewichte w1 <- 1 / (((2*n)/(n^2)) + ((d1^2) / (4*n))) w2 <- 1 / (((2*n)/(n^2)) + ((d2^2) / (4*n))) w3 <- 1 / (((2*n)/(n^2)) + ((d3^2) / (4*n))) w4 <- 1 / (((2*n)/(n^2)) + ((d4^2) / (4*n))) w5 <- 1 / (((2*n)/(n^2)) + ((d5^2) / (4*n))) ws <- c(w1, w2, w3, w4, w5) # Berechnung des 95% metaanalytischen KIs d <- sum(ds * ws) / sum(ws) d - 1.96/sqrt(sum(ws))[1] -0.6135862d + 1.96/sqrt(sum(ws))[1] 0.178598595% KI: [-0.614;0.179]
Man kann nicht davon ausgehen, dass die Darbietung von emotional belastenden Stimuli einen Einfluss auf die durchschnittliche Konzentrationsleistung von Studierenden hat, da sowohl positive als auch negative Werte für den wahren Effekt \(\delta\) plausibel sind.
Sie sind enttäuscht und haben das Gefühl, dass sich die viele Arbeit nicht gelohnt hat, da es so aussieht, als ob emotional belastende Stimuli keinen Einfluss auf die durchschnittliche Konzentrationsleistung von Studierenden haben. Ihre Betreuerin ist jedoch anderer Meinung und glaubt, dass vor allem Experiment 2 sehr vielversprechend ist, da sie sich die Ergebnisse des t-Tests mit ungerichteten Hypothesen etwas genauer angeschaut hat. Sie glaubt, dass der Test nur deshalb bei einem Signifikanzniveau von 0.05 nicht ganz signifikant geworden ist, da noch nicht genügend Daten erhoben wurden und die Power wohl noch etwas zu klein ist.
HinweisErgebnisse der t-Tests mit ungerichteten Hypothesen# Überprüfung der zweiseitigen t-Tests # Experiment 2 zeigt einen p-Wert relativ nahe an 0.05 t.test(Daten1$x1, Daten1$x2, var.equal = TRUE)Two Sample t-test data: Daten1$x1 and Daten1$x2 t = 0.23431, df = 18, p-value = 0.8174 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -0.9770869 1.2223869 sample estimates: mean of x mean of y 0.19766656 0.07501655t.test(Daten2$x1, Daten2$x2, var.equal = TRUE)Two Sample t-test data: Daten2$x1 and Daten2$x2 t = -2.0513, df = 18, p-value = 0.05508 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -1.77519685 0.02122661 sample estimates: mean of x mean of y -0.3573462 0.5196389t.test(Daten3$x1, Daten3$x2, var.equal = TRUE)Two Sample t-test data: Daten3$x1 and Daten3$x2 t = -0.33343, df = 18, p-value = 0.7427 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -1.0944010 0.7946067 sample estimates: mean of x mean of y 0.1873067 0.3372038t.test(Daten4$x1, Daten4$x2, var.equal = TRUE)Two Sample t-test data: Daten4$x1 and Daten4$x2 t = -0.060552, df = 18, p-value = 0.9524 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -1.130185 1.066863 sample estimates: mean of x mean of y -0.12762999 -0.09596875t.test(Daten5$x1, Daten5$x2, var.equal = TRUE)Two Sample t-test data: Daten5$x1 and Daten5$x2 t = -0.36782, df = 18, p-value = 0.7173 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -1.0007232 0.7025292 sample estimates: mean of x mean of y -0.08006336 0.06903360# KI für delta in Experiment 2 ist sehr breit # auch Werte für den wahren Effekt nahe 0 sind plausibel cohen.d(Daten2$x1, Daten2$x2, na.rm = TRUE)Cohen's d d estimate: -0.9173571 (large) 95 percent confidence interval: lower upper -1.90510021 0.07038597Sie “erheben” 7 neue Personen pro Gruppe und erhalten die unten in der Tabelle angegebenen Werte (Hinweis: natürlich sind diese Werte aus der gleichen Verteilung simuliert wie die ursprünglichen Daten). Der folgende Code fügt eine neue Person pro Gruppe zu den Daten von Experiment 2 hinzu:
Daten2 <- rbind(Daten2, c(WERT_x1, WERT_x2)). Sie müssen hier nur die Werte aus der Tabelle zeilenweise angeben und fügen so die neue “Person” dem alten Datensatz hinzu.Person x1 x2 11 -0.811 -2.944 12 -0.019 -0.355 13 0.036 0.494 14 -0.660 1.000 15 1.072 0.756 16 -1.455 0.943 17 -1.870 -0.253 Berechnen Sie nach Hinzufügen jeder neuen Person den p-Wert des t-Tests.
TippLösung# FEHLER: OPTIONAL STOPPING!!! # Simuliere eine neue Personen gro Gruppe in Experiment 2 Daten2 <- rbind(Daten2, c(-0.811, -2.944)) # Überprüfe den p-Wert des t-Tests t.test(Daten2$x1, Daten2$x2, var.equal = TRUE)Two Sample t-test data: Daten2$x1 and Daten2$x2 t = -1.2057, df = 20, p-value = 0.242 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -1.647162 0.440462 sample estimates: mean of x mean of y -0.3985875 0.2047626Daten2 <- rbind(Daten2, c(-0.019, -0.355)) t.test(Daten2$x1, Daten2$x2, var.equal = TRUE)Two Sample t-test data: Daten2$x1 and Daten2$x2 t = -1.1408, df = 22, p-value = 0.2662 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -1.4795973 0.4294554 sample estimates: mean of x mean of y -0.3669552 0.1581157Daten2 <- rbind(Daten2, c(0.036, 0.494)) t.test(Daten2$x1, Daten2$x2, var.equal = TRUE)Two Sample t-test data: Daten2$x1 and Daten2$x2 t = -1.2225, df = 24, p-value = 0.2334 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -1.3976852 0.3578619 sample estimates: mean of x mean of y -0.3359586 0.1839530Daten2 <- rbind(Daten2, c(-0.660, 1.000)) t.test(Daten2$x1, Daten2$x2, var.equal = TRUE)Two Sample t-test data: Daten2$x1 and Daten2$x2 t = -1.5082, df = 26, p-value = 0.1436 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -1.420914 0.218221 sample estimates: mean of x mean of y -0.3591045 0.2422421Daten2 <- rbind(Daten2, c(1.072, 0.756)) t.test(Daten2$x1, Daten2$x2, var.equal = TRUE)Two Sample t-test data: Daten2$x1 and Daten2$x2 t = -1.4039, df = 28, p-value = 0.1713 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -1.3283659 0.2479857 sample estimates: mean of x mean of y -0.2636975 0.2764926Daten2 <- rbind(Daten2, c(-1.455, 0.943)) t.test(Daten2$x1, Daten2$x2, var.equal = TRUE)Two Sample t-test data: Daten2$x1 and Daten2$x2 t = -1.7743, df = 30, p-value = 0.08617 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -1.41173518 0.09912878 sample estimates: mean of x mean of y -0.3381539 0.3181493Daten2 <- rbind(Daten2, c(-1.870, -0.253)) t.test(Daten2$x1, Daten2$x2, var.equal = TRUE)Two Sample t-test data: Daten2$x1 and Daten2$x2 t = -1.9772, df = 32, p-value = 0.05669 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -1.44717284 0.02154328 sample estimates: mean of x mean of y -0.4282625 0.2845523p-Wert für Experiment 2 vor der Zusatzerhebung (n1 = n2 = 10):
0.055
p-Wert nach Erhebung jeweils einer zusätzlichen Person pro Gruppe:
0.242, 0.266, 0.233, 0.144, 0.171, 0.086, 0.057
Man sieht, dass der p-Wert bei der Erhebung zusätzlicher Daten nicht deterministisch kleiner oder größer wird. Hier ist der p-Wert mit 17 Personen pro Gruppe zufällig wieder fast genauso groß, wie nach 10 Personen pro Gruppe.
Frustriert berichten Sie Ihrer Betreuerin, dass die weitere Erhebung nichts gebracht habe und der Test immer noch nicht signifikant ist. Ihre Betreuerin schaut sich die Daten noch einmal genau an und stellt verwundert fest, dass in der zweiten Gruppe eine Person einen sehr niedrigen Wert im Konzentrationstest erzielt hat. Werte kleiner als -2 seien bei diesem Test laut ihrer langjährigen Erfahrung sehr ungewöhnlich. Vermutlich sei eine nicht ausreichende Motivation des Probanden der Grund dafür.
Betrachten Sie die Verteilung der Konzentrationsleistung in Experiment 2 getrennt für beide Gruppen mithilfe eines Boxplots.
TippLösung# FEHLER: RESEARCHER DEGREES OF FREEDOM!!! # Boxplot aus Experiment 2 zeigt einen "Ausreißer" in Gruppe 2 boxplot(Daten2$x1, Daten2$x2)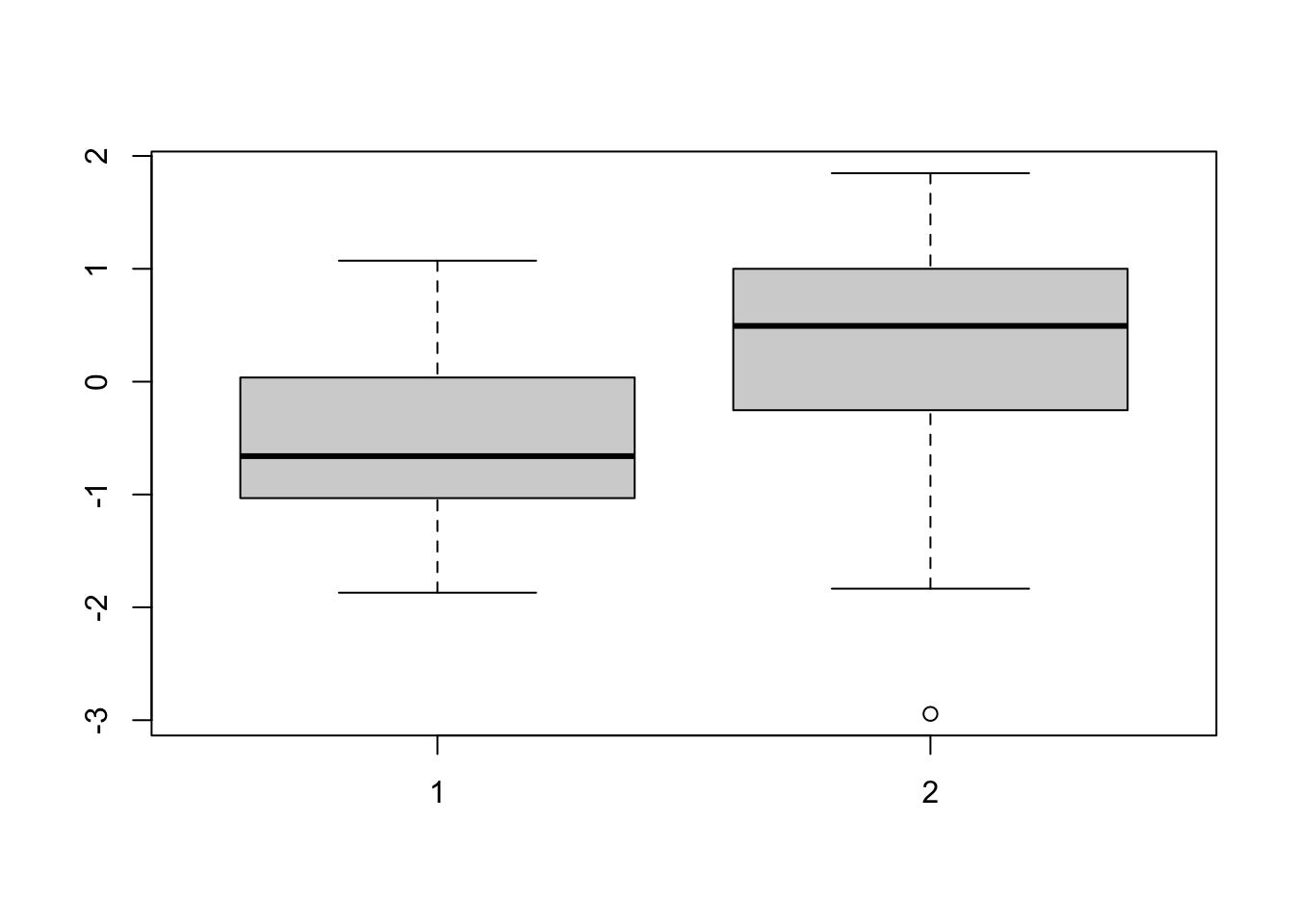
Entfernen Sie den Ausreißer, indem Sie seinen Wert im Datensatz mit NA ersetzen und berechnen Sie erneut den p-Wert des t-Tests.
TippLösung# Ersetze Ausreißer durch NA Daten2[11, "x2"] <- NA # Berechne erneut den p-Wert t.test(Daten2$x1, Daten2$x2, var.equal = TRUE)Two Sample t-test data: Daten2$x1 and Daten2$x2 t = -2.9671, df = 31, p-value = 0.005748 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -1.5432768 -0.2859218 sample estimates: mean of x mean of y -0.4282625 0.4863368p = 0.006 und damit kleiner als 0.05
Ihre Betreuerin ist sehr erfreut, als Sie ihr von dem neuen signifikanten Ergebnis berichten. Sie findet, dass man die Ergebnisse der Bachelorarbeit so auf jeden Fall in einer hochrangigen wissenschaftlichen Zeitschrift veröffentlichen kann. Sie habe sich angesichts der vielversprechenden Ergebnisse alle Daten noch einmal genau angeschaut und sich basierend darauf einige weiterführende Gedanken gemacht. Sie sei mittlerweile der Meinung, dass in Experiment 1 die Wahl der emotional belastenden Stimuli doch nicht so optimal gewählt wurde wie zuvor angenommen. Dies schließe sie vor allem daraus, dass hier der Schätzwert für \(\delta\) tendenziell eher in die andere Richtung zeigt, als in allen anderen Studien. Es sei aber ganz normal, dass bei so vielen Experimenten auch mal eines „nicht funktioniert”. Sie schlägt vor, Experiment 1 für die Veröffentlichung besser wegzulassen, auch um eventuelle kritische Nachfragen der externen Gutachter:innen zu vermeiden und die Chance auf eine Veröffentlichung zu erhöhen.
Führen Sie einen metaanalytischen Hypothesentest mit ungerichteter Alternativhypothese durch und treffen Sie die Testentscheidung mit einem Signifikanzniveau von 0.05. Berücksichtigen Sie dazu nur die Experimente 2, 3, 4 und 5. (Hinweis: Denken Sie daran, für Experiment 2 sowohl den Schätzwert für \(\delta\) als auch das Gewicht neu zu berechnen).
TippLösung# Berechne d und w für Experiment 2 neu d2 <- cohen.d(Daten2$x1, Daten2$x2, na.rm = TRUE)$estimate w2 <- 1 / (((16+17)/(16*17)) + ((d2^2) / (2*(16+17)))) # FEHLER: PUBLICATION BIAS!!! # Berechne metaanalytischen Hypothesentest mit ungerichteter H1 # nur für Experimente 2, 3, 4, 5 ds <- c(d2, d3, d4, d5) ws <- c(w2, w3, w4, w5) d <- sum(ds * ws) / sum(ws) t_statistik <- d * sqrt(sum(ws)) 2 * pnorm(t_statistik)[1] 0.05072004Der p-Wert beträgt 0.051 und ist damit größer als 0.05. Wir entscheiden uns für die Nullhypothese, dass die Präsentation emotional belastender Stimuli keinen Einfluss auf die durchschnittliche Konzentrationsleistung der Studierenden hat.
Sie berichten Ihrer Betreuerin, dass der metaanalytische Hypothesentest leider ganz knapp nicht signifikant ist und Sie fragen sich, ob das dazu führen könnte, dass die Zeitschrift Ihren Artikel ablehnen könnte. Ihre Betreuerin beruhigt Sie. Sie habe erst kürzlich eine neue Theorie gelesen, dass emotional belastende Stimuli vor allem bei Studierenden eher zu einer Reduzierung der durchschnittlichen Konzentrationsfähigkeit führen sollten. Dies sei nach aktuellem Stand bei Weitem die plausibelste inhaltliche Hypothese.
Führen Sie den metaanalytischen Hypothesentest mit gerichteter Alternativhypothese durch, so dass diese mit der neu entdeckten Theorie vereinbar ist. Treffen Sie die Testentscheidung.
TippLösung# FEHLER: HARKING!!! # Berechne Hypothesentest mit linksgerichteter H1 pnorm(t_statistik)[1] 0.02536002Der p-Wert beträgt 0.025 und ist damit kleiner als 0.05. Wir entscheiden uns für die Alternativhypothese, dass Studierende denen emotional belastende Stimuli präsentiert werden, eine niedrigere durchschnittliche Konzentrationsleistung aufweisen als Studierende in der Kontrollgruppe.
Ihre Betreuerin veröffentlicht mit Ihrer Hilfe einen Artikel zu den Ergebnissen in einer renommierten Zeitschrift. Dieser wird aufgrund der überraschenden aber durch die vier konsistenten Studien überzeugenden Ergebnisse viel zitiert und findet auch in mehreren populärwissenschaftlichen Lifestylemagazinen Beachtung. Zwei Jahre später hören Sie auf einer Fachkonferenz einen Vortrag von einer Arbeitsgruppe, die vergeblich versucht hat, Experiment 2 mit einer neuen Stichprobe zu replizieren. Sie fühlen sich von den Ergebnissen der Replikationsstudie in Ihrer Ehre als Forscher:in verletzt und wollen mit einer eigenen Replikationsstudie beweisen, dass Ihre Theorie doch stimmt und die anderen Forscher:innen sich nur nicht gut genug mit der Durchführung solcher Experimente auskennen. Um alle Kritiker:innen zu überzeugen wollen Sie diesmal die Studie vor deren Durchführung präregistrieren.
Führen Sie für Ihre geplante Replikationsstudie eine Stichprobenplanung durch. Wie viele Personen müssen Sie pro Gruppe mindestens erheben, um eine Power von 0.8 bei einem Signifikanzniveau von 0.05 und einer gerichteten Alternativhypothese unter der Annahme erzielen, dass der wahre Effekt \(\delta\) dem Schätzwert aus Experiment 2 der Originalstudie entspricht.
TippLösunglibrary(pwr) # FEHLER: POST HOC POWER!!! # Berechne Stichprobenumfang mit dem Schätzwert d2 als wahres delta pwr.t.test(power = 0.8, sig.level = 0.05, d = -1.034, alternative = "less")Two-sample t test power calculation n = 12.30187 d = -1.034 sig.level = 0.05 power = 0.8 alternative = less NOTE: n is number in *each* groupIm Falle eines wahren Effekts von -1.043 müssen für eine Power von 0.8 mindestens 13 Personen pro Gruppe erhoben werden.
Sie führen die Replikationsstudie mit dem berechneten Stichprobenumfang durch. Sie ziehen dazu wieder zwei einfache Zufallsstichproben aus der gleichen Studierendenpopulation wie die Originalstudie. Sie verwenden die gleichen emotional belastenden Stimuli sowie den gleichen Konzentrationstest.
Wie hoch wäre die Wahrscheinlichkeit, dass der t-Test mit gerichteter Alternativhypothese bei einem Signifikanzniveau von 0.05 erneut signifikant wird (d.h. die Replikation ist erfolgreich), unter der Annahme, dass der wahre Effekt \(\delta\) dem Schätzwert aus Experiment 2 der Originalstudie entspricht?
TippLösungIm Falle, dass der wahre Effekt \(\delta\) dem Schätzwert aus Experiment 2 der Originalstudie von -1.043 entspricht, ist die Wahrscheinlichkeit für eine erfolgreiche Replikation gleich der Power der Studie, also 0.8.
Wie hoch ist die Wahrscheinlichkeit, dass der Test erneut bei einem Signifikanzniveau von 0.05 signifikant wird (d.h. die Replikation ist erfolgreich) tatsächlich? (Hinweis: Schauen Sie im R-Code der Simulation nach, wie hoch der wahre Effekt \(\delta\) in dem vorliegenden Beispiel tatsächlich ist).
TippLösungIm Simulationscode der Datenerhebung werden für beide Gruppen in allen 5 Experimenten unabhängige standardnormalverteilte Zufallsvariablen gezogen. Damit gilt in allen 5 Experimenten \(\mu_{1} - \mu_{2} = 0\), sowie \(\delta = \frac{\mu_{1} - \mu_{2}}{\sigma} = \frac{0 - 0}{1} = 0\) . Die durchschnittliche Konzentrationsleistung von Studierenden denen emotional belastende Stimuli präsentiert werden, unterscheidet sich nicht von der durchschnittlichen Konzentrationsleistung von Studierenden in der Kontrollgruppe. Damit gilt die Nullhypothese und die Wahrscheinlichkeit dafür, dass die Replikationsstudie signifikant wird, entspricht dem Signifikanzniveau von 0.05.
Sie führen die Replikationsstudie durch und stellen voller Bestürzung fest, dass sich der Test für die Nullhypothese entscheidet. Sie sind verzweifelt und verstehen nicht, wie das passieren konnte. Schließlich haben Sie das Experiment genauso durchgeführt wie beim ersten Mal und sogar eine Stichprobenplanung durchgeführt. Diesmal beschließen Sie (statt wieder Ihre Betreuerin zu fragen, was der Grund für den erfolglosen Replikationsversuch sein könnte), sich über die statistischen Grundlagen zu informieren, um in Zukunft Studien mit einem höheren Erkenntnisgewinn durchführen zu können.
Welche Fehler wurden bei der Datenerhebung, Datenauswertung und Interpretation gemacht, die dazu beigetragen haben, dass ein falsch positives Ergebnis Einzug in die wissenschaftliche Literatur gefunden hat?
TippLösung1. Es wurden im Experiment mit dem kleinsten beobachteten p-Wert zusätzliche Personen erhoben und wiederholt Hypothesentests durchgeführt, ohne das Signifikanzniveau zu korrigieren. Damit erhöht sich die Wahrscheinlichkeit für einen Fehler 1. Art. Ein solches Vorgehen wird auch als Optional Stopping bezeichnet.
2. Das Kriterium zum Ausschluss von Ausreißern wurde nach der Datenerhebung und unter Berücksichtigung der beobachteten Verteilung der Daten, sowie des Ergebnisses des Hypothesentests festgelegt.
3. Ein Experiment, dessen Ergebnisse nicht den Hypothesen entspricht wurde nicht veröffentlicht. Dieser sogenannte Publikationsbias führt zu verfälschten Ergebnissen in der Metaanalyse.
4. Die Hypothesen wurde nach der Datenerhebung von ursprünglich ungerichteten Alternativhypothesen in gerichtete Hypothesen (die im Einklang mit den beobachteten Ergebnissen steht) geändert, um ein signifikantes Ergebnis zu erzielen. Ein solches Vorgehen wird in der Literatur häufig auch als HARKING bezeichnet (Hypothesizing After the Results are Known).
5. Im vorliegenden Fall wäre vermutlich eine Metaanalyse mit zufälligen Effekten angemessener, da in den einzelnen Experimenten unterschiedliche emotionale Stimuli und Konzentrationstests verwendet werden. Eine Metaanalyse mit zufälligen Effekten würde aber die oben beschriebenen Fehler nicht korrigieren und stellt für sich genommen keine Absicherung gegen falsch positive Ergebnisse dar!
Erläutern Sie anhand des vorliegenden Beispiels, warum für die Stichprobenplanung von Replikationsstudien nicht der Schätzwert der Originalstudie als wahrer Effekt angenommen werden sollte.
TippLösungDa wir wissen, dass im Falle von nicht präregistrierten Studien die Chance auf das Vorliegen von Publikationsbias und damit die FDR in der psychologischen Forschung vermutlich hoch ist, muss man davon ausgehen, dass die Größe vieler Effekte überschätzt wird. Verwendet man die Punktschätzung aus der Originalstudie für die Stichprobenplanung der Replikationsstudie, ist die tatsächliche Power unter Umständen deutlich geringer als vermutet. Damit ist auch die Wahrscheinlichkeit für eine erfolgreiche Replikation unter Umständen deutlich kleiner als angenommen. Eine bessere Strategie als den Punktschätzer aus der Originalstudie für die Stichprobenplanung zu verwenden kann es sein, die konservative Grenze des Konfidenzintervalls für \(\delta\) zu verwenden. Bei Vorliegen von Optional Stopping und/oder p-Hacking kann dieser Wert im Betrag aber immer noch deutlich zu groß sein. Zum Beispiel geht das Konfidenzintervall in Experiment 2 der Originalstudie von -1.790 bis -0.277. Noch besser ist es also, den angenommenen Mindesteffekt für die Replikationsstudie theoriebasiert, möglichst klein und eventuell sogar weitgehend unabhängig von den Ergebnissen der Originalstudie festzulegen.
Haben Replikationsstudien in Wahrheit eine geringe Power, ist eine nicht erfolgreiche Replikation unter Umständen wahrscheinlicher als eine erfolgreiche Replikation (falls \(1 - \beta < 0.5\), oder sogar\(\ \delta = 0\)). Die Replikationsstudie trägt dann wenig zum Erkenntnisgewinn bei. Zusätzlich ist eine gemeinsame Metaanalyse von Original- und Replikationsstudie nicht angemessen, falls Publikationsbias und/oder andere methodische Probleme wie p-Hacking naheliegen.
Bonusaufgabe: Welche Anreizstrukturen im wissenschaftlichen Publikationssystem könnten zu den hier vorliegenden Problemen beitragen, bzw. diese weiter verstärken?
TippLösung1. Signifikante Studien haben eine höhere Chance, von wissenschaftlichen Zeitschriften akzeptiert zu werden. Publikationen in wissenschaftlichen Zeitschriften sind die wichtigste Voraussetzung für eine wissenschaftliche Karriere. Dies erzeugt Anreize, Researcher Degrees of Freedom auszunutzen, um signifikante Ergebnisse zu produzieren.
2. Studien mit überraschenden Ergebnissen haben eine höhere Chance, von wissenschaftlichen Zeitschriften akzeptiert zu werden. Dies erzeugt Anreize, viele kleine Studien zu wenig erforschten Themen durchzuführen, anstatt wenige aufwendige Studien mit großen Stichproben zur Absicherung gut untersuchter Effekte durchzuführen. Dies trägt durch kleine Studien mit niedriger Power zu einer hohen FDR in der veröffentlichten Literatur bei.
3. Studien mit in sich konsistenten Teilergebnissen haben eine höhere Chance, von wissenschaftlichen Zeitschriften akzeptiert zu werden. Dies erzeugt Anreize, nicht „funktionierende”, nicht signifikante Experimente wegzulassen, um im Artikel ein in sich konsistentes Narrativ präsentieren zu können. Dies trägt durch Publikationsbias ebenfalls zu einer erhöhten FDR bei, da signifikante Ergebnisse in der Literatur überrepräsentiert sind.
Bonusaufgabe: Warum könnten die an diesem Beispiel aufgezeigten Probleme in der psychologischen Forschungslandschaft durch die Verwendung eines Signifikanzniveaus von 0.005 und großen Stichproben in Kombination mit Präregistrierung verbessert werden?
TippLösung1. Unabhängig von Publikationsbias und Researcher Degrees of Freedom führt ein niedriges Signifikanzniveau in Kombination mit einer hohen Power zu einer niedrigen FDR und damit zu einem höheren Vertrauen in signifikante Studienergebnisse.
2. Zusätzlich wird es bei einem niedrigen Signifikanzniveau von 0.005 deutlich schwieriger, Ergebnisse durch die Anwendung von Researcher Degrees of Freedom signifikant werden zu lassen, da die Voraussetzungen für ein signifikantes Ergebnis deutlich strenger sind.
3. Studien mit großen Stichproben haben generell einen höheren Erkenntnisgewinn, da sie viel genauere Parameterschätzungen erlauben. Dies führt dazu, dass große Studien auch bei nicht signifikanten Ergebnissen leichter zu veröffentlichen sind und daher Publikationsbias nicht mehr so ein großes Problem ist. Sind große Stichproben für eine Veröffentlichung Voraussetzung, ist es außerdem keine gute Strategie mehr, viele wenig aufwendige Studien mit kleinen Stichproben durchzuführen um an Publikationen zu kommen.
4. Der hohe Aufwand von großen Studien mit hoher Power führt indirekt häufig dazu, dass große Studien auch eine höhere methodische Qualität aufweisen. Die beteiligten Wissenschaftler:innen müssen sich stärker committen, da mehr Zeit und Geld in die Durchführung der Studie investiert wird. Oft müssen auch mehrere Arbeitsgruppen zusammenarbeiten, um die großen Stichprobenzahlen erreichen zu können. Dies erhöht die Chance, dass Personen an der Planung und Auswertung der Studie beteiligt sind, die sich methodisch besser auskennen.
5. Präregistrierung soll dazu führen, Researcher Degrees of Freedom und damit auch die FDR zu reduzieren. Außerdem können Präregistrierungen auf öffentlichen Servern dazu beitragen, das Ausmaß von Publikationsbias besser einzuschätzen. Selbst wenn die in der Präregistrierung geplanten Studien nicht veröffentlicht werden, kann zumindest die Information über präregistrierte Studien bei der Abschätzung von Publikationsbias berücksichtigt werden. Noch vorteilhafter ist die Durchführung von Preregistered Reports, bei denen die Präregistrierung vor Durchführung der Studie begutachtet wird und eine Veröffentlichung des finalen Artikels, bei Einhaltung des präregistrierten Studienplans, unabhängig von den tatsächlichen Ergebnissen durch eine wissenschaftliche Zeitschrift garantiert wird.