Übungsblatt 5

Weitere Verfahren im ein- und zweifaktoriellen varianzanalytischen Modell

  1. Sie interessieren sich dafür, inwiefern sich Berufsgruppen (Sacharbeiterinnen (S) vs. Beamtinnen (B) vs. Dienstleisterinnen (D)) in ihrer mittleren (stetigen) Gewissenhaftigkeit unterscheiden. Sie wählen ein einfaktorielles varianzanalytisches Modell:

    \(Y_{ij} = \mu_{j} + \varepsilon_{ij}\) mit \(j = S,B,D\) und \(Y_{ij}\ \sim\ N(\mu_{j}\), \(\sigma^{2}\))

    Übersetzen Sie die folgenden Fragestellungen jeweils in statistische Hypothesen. Geben Sie sowohl die Einzelhypothesen als auch (falls notwendig) die zusammengesetzten Hypothesen an:

    1. Sind die Beamtinnen im Mittel gewissenhafter als Dienstleisterinnen?

      \[H_{0}:\mu_{B} - \mu_{D} \leq 0\] \[H_{1}:\mu_{B} - \mu_{D} > 0\]

    2. Sind die Sachbearbeiterinnen im Mittel gewissenhafter als Dienstleisterinnen, aber weniger gewissenhaft als Beamtinnen?

      \[H_{01}:\mu_{S} - \mu_{D} \leq 0\] \[H_{11}:\mu_{S} - \mu_{D} > 0\] \[H_{02}:\mu_{S} - \mu_{B} \geq 0\] \[H_{12}:\mu_{S} - \mu_{B} < 0\]

      \[H_{0}:H_{01}\ oder{\ H}_{02}\] \[H_{1}:H_{11}\ und{\ H}_{12}\]

    3. Ist die Differenz zwischen der mittleren Gewissenhaftigkeit von Beamtinnen und Sachbearbeiterinnen größer als 10?

      \[H_{0}:\mu_{B} - \mu_{S} \leq 10\] \[H_{1}:\mu_{B} - \mu_{S} > 10\]

    4. Sind Beamtinnen im Mittel sowohl gewissenhafter als Sachbearbeiterinnen als auch als Dienstleisterinnen?

      \[H_{01}:\mu_{B} - \mu_{S} \leq 0\] \[H_{11}:\mu_{B} - \mu_{S} > 0\]

      \[H_{02}:\mu_{B} - \mu_{D} \leq 0\] \[H_{12}:\mu_{B} - \mu_{D} > 0\]

      \[H_{0}:H_{01}\ oder{\ H}_{02}\] \[H_{1}:H_{11}\ und{\ H}_{12}\]

    5. Ist der Gesamtmittelwert der Gewissenhaftigkeit in den drei Berufsgruppen größer als 100?

      \[H_{0}:\mu \leq 100\] \[H_{1}:\mu > 100\]

    6. Sind Beamtinnen im Mittel mehr als doppelt so gewissenhaft wie Dienstleisterinnen?

      \[\mu_{B} > 2\mu_{D}\]

      \[\Leftrightarrow \mu_{B} - 2\mu_{D} > 0\]

      also:

      \[H_{0}:\ \mu_{B} - 2\mu_{D} \leq 0\] \[H_{1}:\ \mu_{B} - 2\mu_{D} > 0\]

    7. Ist die mittlere Differenz in der Gewissenhaftigkeit zwischen Beamtinnen und Sachbearbeiterinnen größer als zwischen Sachbearbeiterinnen und Dienstleisterinnen?

      \[\mu_{B} - \mu_{S} > \mu_{S} - \mu_{D}\]

      \[\Leftrightarrow \mu_{B} - \mu_{S} - \mu_{S} + \mu_{D} > 0\]

      \[\Leftrightarrow \mu_{B} - 2\mu_{S} + \mu_{D} > 0\]

      also: \[H_{0}:\ \mu_{B} - 2\mu_{S} + \mu_{D} \leq 0\] \[H_{1}:\ \mu_{B} - 2\mu_{S} + \mu_{D} > 0\]

  2. Sie wollen untersuchen, wie stark sich Psychiatriepatientinnen mit Abitur (A) und Psychiatriepatientinnen mit Hochschulabschluss (H) jeweils in ihrer durchschnittlichen (stetigen) Zeit (Einheit Tage) bis zur Entlassung aus der Klinik von Psychiatriepatientinnen mit mittlerer Reife (M) unterscheiden.

    ## package für spezifische Konfidenzintervalle und Hypothesentests im
## varianzanalytischen Modell laden (ggf zuerst installieren)
library(multcomp)

## ANLEITUNG ZUR VERWENDUNG DES PAKETS

## Daten einlesen:
Daten <- read.csv2('DATENSATZ.CSV', stringsAsFactors = TRUE)

## aov-Objekt speichern:
fit_aov <- aov(AV ~ Faktor, data = Daten)

## Zunaechst muessen wir die Nullhypothesen einzeln als character
## definieren. Alternativ koennen die Hypothesen auch mithilfe einer 
## Kontrastmatrix spezifiziert werden (siehe Dokumentation von multcomp).
##
## Hinweis: Auch wenn wir, wie in Aufgabe 8, Konfidenzintervalle 
## berechnen, muessen wir in R Hypothesen formulieren. In diesem Fall
## muessen die Hypothesen jeweils ungerichtet mit Referenzwert 0
## angegeben werden:
##
## Allgemeine Syntax:
## Der Referenzwert muss immer auf der rechten Seite stehen
## gleich: ==
## kleiner-gleich: <=
## größer-gleich: >=
## minus: -
## plus: +
## mal: *
## geteilt: /
## Auch Klammersetzung ist möglich, z.B.
## '0.5*(Hochschule + Abitur) - mittlere_Reife == 0'
##
## Wichtig: Exakte Namen der Faktorstufen verwenden! Zudem sollten die
## Namen der Faktorstufen keine Leer- oder Sonderzeichen enthalten.
## Sonst vorher umbenennen. Die Namen der Faktorstufen können
## Sie sich mithilfe der Funktion levels() ausgeben lassen:
levels(Daten$Faktor)

## Hypothesen für unser Beispiel:
hyp1 <- 'Stufe1 - Stufe2 == 0'
hyp2 <- 'Stufe3 - Stufe2 == 0'

## Die einzelnen Hypothesen werden dann in einem
## character-Vektor zusammengefasst:
hyps <- c(hyp1, hyp2)

## Als naechstes wird mithilfe der mcp-Funktion aus dem Hypothesenvektor
## ein Kontrastobjekt erstellt. Dies ist notwendig, damit die sprachlich
## formulierten Hypothesen von R spaeter intern automatisch in
## Kontrastgewichte uebersetzt werden koennen. Als Argument wird
## Name_des_Faktors = Kontrasthypothesenvektor gesetzt:
kontraste <- mcp(Faktor = hyps)

## Mithilfe der glht-Funktion wird dann ein glht Objekt erstellt. Das
## erste Argument ist das aov Objekt (Output der aov-Funktion). Das
## zweite Argument (linfct) ist das Kontrastobjekt (Output der
## mcp-Funktion). Das Ergebnis sollte wie immer in einem eigenen Objekt
## gespeichert werden:
fit <- glht(fit_aov, linfct = kontraste)

## 95%-Konfidenzintervalle (calpha = univariate_calpha() bedeutet, dass
## die KIs ohne Korrektur berechnet werden)
confint(fit, level = 0.95, calpha = univariate_calpha())

## Testergebnisse anzeigen (test = adjusted(type = "single-step") bedeutet, 
## dass die p-Werte mit der Tukey Methode korrigiert werden):
summary(fit, test = adjusted(type = "single-step"))

## Unkorrigierte Testergebnisse anzeigen (test=test_univariate() bedeutet, 
## dass die p-Werte ohne Korrektur berechnet werden):
summary(fit, test = univariate())

## Testergebnisse mit Bonferroni Methode anzeigen (test = adjusted(type = "bonferroni") bedeutet, 
## dass die p-Werte mit der Beonferroni Methode korrigiert werden)
summary(fit, test = adjusted(type = "bonferroni"))

    1. Stellen Sie die Modellgleichung auf.

      \[Y_{ij} = \mu_{j} + \varepsilon_{ij} \text{ mit } j = A,\ H,M\]

    2. Übersetzen Sie die interessierenden Größen in Modellparameter.

      \[\mu_{A} - \mu_{M}\]
      \[\mu_{H} - \mu_{M}\]

    3. Laden Sie den Datensatz herunter. Berechnen Sie 95%-Konfidenzintervalle für die interessierenden Größen (siehe oben die Anleitung zur Durchführung von Einzelvergleichen in R) und interpretieren Sie diese.

      library(multcomp)
      ## Daten einlesen:
entlassung <- read.csv2('Entlassung.csv', stringsAsFactors = TRUE)
      ## aov-Objekt speichern:
fit_aov <- aov(Tage_bis_zur_Entlassung ~ Bildung, data = entlassung)

## Wichtig: Exakte Namen der Faktorstufen verwenden! Zudem sollten die
## Namen der Faktorstufen keine Leer- oder Sonderzeichen enthalten.
## Sonst vorher umbenennen. Die Namen der Faktorstufen können
## Sie sich mithilfe der Funktion levels() ausgeben lassen:
levels(entlassung$Bildung)
      [1] "Abitur"         "Hochschule"     "mittlere_Reife"
      ## Hypothesen für unser Beispiel:
hyp1 <- 'Abitur - mittlere_Reife == 0'
hyp2 <- 'Hochschule - mittlere_Reife == 0'

hyps <- c(hyp1, hyp2)

kontraste <- mcp(Bildung = hyps)

fit <- glht(fit_aov, linfct = kontraste)

## 95%-Konfidenzintervalle (calpha = univariate_calpha() bedeutet, dass
## die KIs ohne Korrektur berechnet werden)
confint(fit, level = 0.95, calpha = univariate_calpha())
      
  Simultaneous Confidence Intervals

Multiple Comparisons of Means: User-defined Contrasts


Fit: aov(formula = Tage_bis_zur_Entlassung ~ Bildung, data = entlassung)

Quantile = 1.9639
95% confidence level


Linear Hypotheses:
                                 Estimate lwr      upr     
Abitur - mittlere_Reife == 0     -17.5600 -19.1946 -15.9254
Hochschule - mittlere_Reife == 0 -25.7300 -27.3646 -24.0954

      Wir gehen davon aus, dass die durchschnittliche Zeit zur Entlassung für Psychiatriepatientinnen mit Abitur zwischen 19.195 und 15.925 Tage kürzer ist als für Psychiatriepatientinnen mit mittlerer Reife.

      Wir gehen davon aus, dass die durchschnittliche Zeit zur Entlassung für Psychiatriepatientinnen mit Hochschulabschluss zwischen 27.365 und 24.095 Tage kürzer ist als für Psychiatriepatientinnen mit mittlerer Reife.

      Anmerkung: Ein direkter Vergleich der Patientinnen mit Abitur und der Patientinnen mit Hochschulabschluss ist hier streng genommen nicht möglich. Dafür müsste ein zusätzliches Konfidenzintervall für \(\mu_{A} - \mu_{H}\) betrachtet werden. Dies war jedoch nicht Bestandteil der Fragestellung.

  3. Sie wollen untersuchen, ob bei mindestens einer von zwei Therapieformen (Kognitive Verhaltenstherapie (KVT), tiefenpsychologisch fundierte Therapie (TFT)) die mittlere (stetige) Depressionsschwere nach der Therapie niedriger ist als nach gar keiner Therapie (KT).

    1. Stellen Sie die Modellgleichung auf.

      \(Y_{ij} = \mu_{j} + \varepsilon_{ij}\) mit \(j = KVT,\ TFT,\ KT\)

    2. Stellen Sie die statistischen Hypothesen auf.

      Einzelhypothesen:
      \(H_{01}:\ \mu_{KVT} - \mu_{KT} \geq 0\)
      \(H_{11}:\ \mu_{KVT} - \mu_{KT} < 0\)

      \(H_{02}:\ \mu_{TFT} - \mu_{KT} \geq 0\)
      \(H_{12}:\ \mu_{TFT} - \mu_{KT} < 0\)

      Zusammengesetzte Hypothesen:
      \(H_{0}:\ H_{01}\ und\) \(H_{02}\)
      \(H_{1}:\) \(H_{11}\ oder\ H_{12}\)

    3. Laden Sie den Datensatz herunter und testen Sie die Hypothesen in R (siehe oben die Anleitung zur Durchführung von Einzelvergleichen in R). Welche Entscheidung treffen Sie bei einem Signifikanzniveau von \(0.005\)? Interpretieren Sie diese inhaltlich.

      ## Daten einlesen
depression <- read.csv2('Depression.csv', stringsAsFactors = TRUE)
      ## aov Objekt erstellen
fit_aov <- aov(Depressionsschwere ~ Therapieform, data = depression)

## Hypothesen für unser Beispiel:
hyp1 <- 'KVT - Kontrolle >= 0'
hyp2 <- 'TFT - Kontrolle >= 0'
hyps <- c(hyp1, hyp2)

## Erstellen eines Kontrastobjekts
kontraste <- mcp(Therapieform = hyps)

## Erstellen eines glht Objekts
fit <- glht(fit_aov, linfct = kontraste)

## Testergebnisse anzeigen (test = adjusted(type = "single-step") bedeutet, 
## dass die p-Werte mit der Tukey Methode korrigiert werden):
summary(fit, test = adjusted(type = "single-step"))
      
  Simultaneous Tests for General Linear Hypotheses

Multiple Comparisons of Means: User-defined Contrasts


Fit: aov(formula = Depressionsschwere ~ Therapieform, data = depression)

Linear Hypotheses:
                     Estimate Std. Error t value Pr(<t)    
KVT - Kontrolle >= 0  -15.635      1.568  -9.971 <1e-10 ***
TFT - Kontrolle >= 0  -31.605      1.568 -20.156 <1e-10 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Adjusted p values reported -- single-step method)

      Da es sich um eine zusammengesetzte Alternativhypothese mit „oder” handelt, müssen die p-Werte der Einzeltests korrigiert werden. Da wir die Hypothesen im Rahmen eines einfaktoriellen varianzanalytischen Modells untersuchen, können wir für die Korrektur die Tukey Methode (heißt hier in R „single-step method”) verwenden, die eine höhere Power aufweist als die Bonferroni Methode.

      Beide korrigierten p-Werte sind kleiner als \(\alpha^{*} = 0.005\) . Wir entscheiden uns also für die zusammengesetzte Alternativhypothese und gehen davon aus, dass nach mindestens einer der beiden Psychotherapien die mittlere Depressionsschwere nach der Therapie niedriger ist als nach gar keiner Therapie.

      Anmerkung 1: Der zusammengesetzte Hypothesentest sagt uns nichts darüber aus, welche der Therapien wirkt. Interessieren wir uns zusätzlich auch für die Einzelhypothesen ist das Signifikanzniveau des zusammengesetzten Hypothesentests (also die FWER) für diese zusätzlichen Fragestellungen eher uninteressant und es sollten besser die unkorrigierten p-Werte betrachtet werden. Die interessante zu kontrollierende Größe für die zusätzlichen Fragestellungen ist hier eher die FDR. Eine niedrige FDR stellen wir indirekt durch ein niedriges Signifikanzniveau und eine hohe Power (große Stichprobe) sicher.

  4. Geben Sie für die folgenden Fragestellungen jeweils an, wie viele einzelne Hypothesentests Sie durchführen müssten und ob sie die p-Werte bzw. Signifikanzniveaus dieser einzelnen Tests korrigieren würden.

    1. Sie interessieren sich für die stetige Gewissenhaftigkeit von Beamtinnen, Selbstständigen und Angestellten und wollen wissen, ob sich mindestens zwei dieser Gruppen in ihrer mittleren Gewissenhaftigkeit unterscheiden.

      Nur ein Omnibustest, also keine Korrektur.

    2. Sie interessieren sich für die Gewissenhaftigkeit von Beamtinnen, Selbstständigen und Angestellten und wollen wissen, ob sich alle Gruppen in ihrer mittleren Gewissenhaftigkeit unterscheiden.

      Zusammengesetzter Hypothesentest mit drei einzelnen Hypothesentests. Keine Korrektur, da „und”-Verknüpfung in der zusammengesetzen \(H_{1}\).

    3. Sie interessieren sich für die Gewissenhaftigkeit von Beamtinnen, Selbstständigen und Angestellten und wollen wissen, welche dieser Gruppen sich in ihrer mittleren Gewissenhaftigkeit unterscheiden.

      Drei einzelne Hypothesentests, wobei wir uns für die einzelnen Hypothesen interessieren. Keine Korrektur (aber natürlich geringes Signifikanzniveau und hohe Power zur Kontrolle der FDR).

    4. In einem ersten Teil Ihrer Studie wollen Sie überprüfen, ob Beamtinnen gewissenhafter als Selbstständige sind. Im zweiten Teil Ihrer Studie wollen Sie anhand der gleichen Stichprobe überprüfen, ob verheiratete Beamtinnen gewissenhafter als nicht verheiratete Beamtinnen sind.

      Zwei einzelne Hypothesentests, wobei wir uns für die einzelnen Hypothesen interessieren. Keine Korrektur (aber natürlich geringes Signifikanzniveau und hohe Power zur Kontrolle der FDR).

    5. Sie führen zwei Studien mit unterschiedlichen Stichproben durch. In der ersten Studie wollen Sie überprüfen, ob Beamtinnen gewissenhafter als Selbstständige sind. In der zweiten Studie wollen Sie überprüfen, ob verheiratete Beamtinnen gewissenhafter als nicht verheiratete Beamtinnen sind.

      Gleiche Situation wie in Teilaufgabe d: Zwei einzelne Hypothesentests, wobei wir uns für die einzelnen Hypothesen interessieren. Keine Korrektur (aber natürlich geringes Signifikanzniveau und hohe Power zur Kontrolle der FDR).

    6. Sie wollen überprüfen, ob es einen positiven Zusammenhang zwischen den beiden stetigen Variablen Lebenszufriedenheit und Einkommen gibt und haben hierfür Daten aus vier verschiedenen Studien vorliegen.

      Kombinierter Hypothesentest im Rahmen einer Metaanalyse

  5. Meyer et al. (2013) wollten untersuchen, ob bei Texas Hold’em Poker Glück oder Können entscheidender ist. 300 Versuchspersonen erhielten 10 Euro Startkapital und spielten 60 Hände Poker an Tischen mit je 6 Personen. Als abhängige Variable wurde erhoben, wie viel Geld die Spielerinnen am Ende des Spiels noch übrig hatten. Eine Hälfte der Spielerinnen waren „Experteninnen”, die andere Hälfte waren „Durchschnittsspielerinnen”. Um den Einfluss von Glück beim Pokern untersuchen zu können, wurde jede Spieler*in einer von drei Bedingungen zugeteilt: Ein Drittel der Spielerinnen erhielt während des kompletten Spiels besonders gute Karten, ein Drittel besonders schlechte Karten und ein Drittel durchschnittlich gute Karten.

    1. Welches Design liegt hier vor?

      Es liegt ein \(2\ x\ 3\)-Design vor: Faktor „Können” mit zwei Stufen (Durchschnittsspielerinnen, Experteninnen), Faktor „Glück” mit drei Stufen (durchschnittliche Karten, gute Karten, schlechte Karten).

    2. Wie lautet die Modellgleichung in Darstellung 1?

      \(Y_{ijk} = \mu_{jk} + \varepsilon_{ijk}\) mit \(j = D,\ E\) und \(k = DK,\ GK,\ SK\)

    3. Tragen Sie alle Erwartungswerte \(\mu_{jk}\), \(\mu_{j \cdot}\) und \(\mu_{\cdot k}\) sowie den Gesamterwartungswert \(\mu\) in eine Tabelle ein. Die Spalten seien dabei für den Faktor „Glück “, die Zeilen seien für den Faktor „Können” vorgesehen.

      durchschnittliche Karten gute Karten schlechte Karten
      Durchschnittsspieler*in \(\mu_{D\_ DK}\) \(\mu_{D\_ GK}\) \(\mu_{D\_ SK}\) \(\mu_{D \cdot}\)
      Expert*in \(\mu_{E\_ DK}\) \(\mu_{E\_ GK}\) \(\mu_{E\_ SK}\) \(\mu_{E \cdot}\)
      \(\mu_{\cdot DK}\) \(\mu_{\cdot GK}\) \(\mu_{\cdot SK}\) \(\mu\)

    4. Laden Sie den Datensatz zur Studie von Meyer et al. (2013) herunter, laden Sie ihn in R ein und speichern Sie ihn als Objekt mit dem Namen „Daten” ab. Führen Sie alle Omnibustests in R durch. Sie können der Funktion aov() mit einem * mehrere UVs zuweisen: aov(AV ~ UV1 * UV2, data = Daten). Speichern Sie das Ergebnis der ANOVA mit dem Namen „fit” ab und rufen Sie die Ergebnisse danach mit summary(fit) auf. Welche Testentscheidungen treffen Sie?

      ## Daten einlesen
Daten <- read.csv2('Poker.csv', stringsAsFactors = TRUE)
      ## Omnibustests
fit <- aov(Geldbetrag_am_Ende ~ Koennen * Glueck, Daten)
summary(fit)
                      Df Sum Sq Mean Sq F value  Pr(>F)    
Koennen          1     49    49.2   2.739 0.09901 .  
Glueck           2   2647  1323.3  73.712 < 2e-16 ***
Koennen:Glueck   2    219   109.5   6.100 0.00254 ** 
Residuals      294   5278    18.0                    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

      Interaktionseffekt: \(p = 0.00254\ < \ 0.005 = \alpha\) Entscheidung für \(H_{1}\). Man geht davon aus, dass in der Population eine Interaktion zwischen den Faktoren „Glück” und „Können” vorliegt.

      Haupteffekt „Können”: \(p = 0.09901\ > \ 0.005 = \alpha\ \) Entscheidung für \(H_{0}\). Man geht davon aus, dass in der Population kein Haupteffekt des Faktors „Können” vorliegt.

      Haupteffekt „Glück”: \(p = 2 \cdot 10^{- 16}\ < \ 0.005\) Entscheidung für \(H_{1}\). Man geht davon aus, dass in der Population ein Haupteffekt des Faktors „Glück” vorliegt.

    5. Bonus: Berechnen Sie ungerichtete Hypothesentests (Signifikanzniveau von 0.005) und 95%-Konfidenzintervalle für alle paarweisen Erwartungswertdifferenzen mithilfe des multcomp Pakets. (Hinweis: Siehe Anleitung unten mit mcp(Kombinierter_Faktor = „Tukey")).

      library(multcomp)
library(forcats) # fuer die Funktion fct_cross()

## Daten einlesen:
## Hinweis: Durch stringsAsFactors = TRUE können wir gleich beim Einlesen
## dafür sorgen, dass Spalten die Text enthalten gleich in den Datentyp
## factor umgewandelt werden. Dieser Schritt vereinfacht die nachfolgenden
## Befehle deutlich.
Daten <- read.csv2('DATENSATZ.CSV', stringsAsFactors = TRUE)

## Die beiden Faktoren zu einem Faktor zusammenfassen und zum Datensatz hinzufuegen
Daten$Kombinierter_Faktor <- fct_cross(Daten$Faktor1, Daten$Faktor2, sep = '_')
# neue Levels anzeigen (Levels sollten keine Leerzeichen enthalten!)
levels(Daten$Kombinierter_Faktor)

## aov-Objekt mit kombiniertem Faktor erstellen:
fit_aov <- aov(AV ~ Kombinierter_Faktor, data = Daten)

## Hypothesen aufstellen bezogen auf den kombinierten Faktor.
## Hinweis: Sollten _alle_ paarweisen Vergleiche von Interesse sein,
## kann man sich das Aufstellen aller Hypothesen in der angegebenen 
## Form auch sparen und statt dessen unten im mcp()-Befehl auch einfach
## mcp(Kombinierter_Faktor = "Tukey")
## schreiben.
hyps <- c('Faktor1Stufe1_Faktor2Stufe1 - Faktor1Stufe1_Faktor2Stufe2 == 0',
          'Faktor2Stufe1_Faktor1Stufe2 - Faktor1Stufe1_Faktor2Stufe2 == 0',
          'etc...')


## Rest funktioniert wie im einfaktoriellen Modell
kontraste <- mcp(Kombinierter_Faktor = hyps)
fit <- glht(fit_aov, linfct = kontraste)
summary(fit, test = univariate())
confint(fit, level = 0.95, calpha = univariate_calpha())
      options(width = 200) # um Tabellenumbrüche zu vermeiden. Outputs ggf. scrollen nach rechts/links

#Ungerichtete Hypothesentests und Konfidenzintervalle für alle paarweisen Differenzen
library(forcats)
library(multcomp)
## Die beiden Faktoren zu einem Faktor zusammenfassen und zum Datensatz hinzufuegen
Daten$Koennen_Glueck <- fct_cross(Daten$Koennen, Daten$Glueck, sep = '_')
# neue Levels anzeigen
levels(Daten$Koennen_Glueck)
      [1] "Durchschnitt_durchschnittlicheKarten" "ExpertIn_durchschnittlicheKarten"     "Durchschnitt_guteKarten"              "ExpertIn_guteKarten"                  "Durchschnitt_schlechteKarten"        
[6] "ExpertIn_schlechteKarten"            
      ## Vereinfachte Syntax für alle paarwiesen Parameterdifferenzen:
hyps <- mcp(Koennen_Glueck = "Tukey") # hat erstmal nichts mit der Tukey Korrektur zu tun
## Rest wie im einfaktoriellen Modell (nur mit dem kombinierten Faktor)
fit_aov <- aov(Geldbetrag_am_Ende ~ Koennen_Glueck, Daten)
fit <- glht(fit_aov, hyps)
summary(fit, test = univariate()) # unkorrigierte p-Werte
      
  Simultaneous Tests for General Linear Hypotheses

Multiple Comparisons of Means: Tukey Contrasts


Fit: aov(formula = Geldbetrag_am_Ende ~ Koennen_Glueck, data = Daten)

Linear Hypotheses:
                                                                             Estimate Std. Error t value Pr(>|t|)    
ExpertIn_durchschnittlicheKarten - Durchschnitt_durchschnittlicheKarten == 0   1.2244     0.8474   1.445 0.149553    
Durchschnitt_guteKarten - Durchschnitt_durchschnittlicheKarten == 0            4.0898     0.8474   4.826 2.24e-06 ***
ExpertIn_guteKarten - Durchschnitt_durchschnittlicheKarten == 0                2.6302     0.8474   3.104 0.002096 ** 
Durchschnitt_schlechteKarten - Durchschnitt_durchschnittlicheKarten == 0      -5.1800     0.8474  -6.113 3.11e-09 ***
ExpertIn_schlechteKarten - Durchschnitt_durchschnittlicheKarten == 0          -2.5158     0.8474  -2.969 0.003235 ** 
Durchschnitt_guteKarten - ExpertIn_durchschnittlicheKarten == 0                2.8654     0.8474   3.381 0.000819 ***
ExpertIn_guteKarten - ExpertIn_durchschnittlicheKarten == 0                    1.4058     0.8474   1.659 0.098190 .  
Durchschnitt_schlechteKarten - ExpertIn_durchschnittlicheKarten == 0          -6.4044     0.8474  -7.558 5.24e-13 ***
ExpertIn_schlechteKarten - ExpertIn_durchschnittlicheKarten == 0              -3.7402     0.8474  -4.414 1.43e-05 ***
ExpertIn_guteKarten - Durchschnitt_guteKarten == 0                            -1.4596     0.8474  -1.722 0.086040 .  
Durchschnitt_schlechteKarten - Durchschnitt_guteKarten == 0                   -9.2698     0.8474 -10.939  < 2e-16 ***
ExpertIn_schlechteKarten - Durchschnitt_guteKarten == 0                       -6.6056     0.8474  -7.795 1.12e-13 ***
Durchschnitt_schlechteKarten - ExpertIn_guteKarten == 0                       -7.8102     0.8474  -9.217  < 2e-16 ***
ExpertIn_schlechteKarten - ExpertIn_guteKarten == 0                           -5.1460     0.8474  -6.073 3.88e-09 ***
ExpertIn_schlechteKarten - Durchschnitt_schlechteKarten == 0                   2.6642     0.8474   3.144 0.001837 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Univariate p values reported)
      confint(fit, calpha = univariate_calpha()) # unkorrigiertes Konfidenzniveau
      
  Simultaneous Confidence Intervals

Multiple Comparisons of Means: Tukey Contrasts


Fit: aov(formula = Geldbetrag_am_Ende ~ Koennen_Glueck, data = Daten)

Quantile = 1.9681
95% confidence level


Linear Hypotheses:
                                                                             Estimate lwr      upr     
ExpertIn_durchschnittlicheKarten - Durchschnitt_durchschnittlicheKarten == 0   1.2244  -0.4433   2.8921
Durchschnitt_guteKarten - Durchschnitt_durchschnittlicheKarten == 0            4.0898   2.4221   5.7575
ExpertIn_guteKarten - Durchschnitt_durchschnittlicheKarten == 0                2.6302   0.9625   4.2979
Durchschnitt_schlechteKarten - Durchschnitt_durchschnittlicheKarten == 0      -5.1800  -6.8477  -3.5123
ExpertIn_schlechteKarten - Durchschnitt_durchschnittlicheKarten == 0          -2.5158  -4.1835  -0.8481
Durchschnitt_guteKarten - ExpertIn_durchschnittlicheKarten == 0                2.8654   1.1977   4.5331
ExpertIn_guteKarten - ExpertIn_durchschnittlicheKarten == 0                    1.4058  -0.2619   3.0735
Durchschnitt_schlechteKarten - ExpertIn_durchschnittlicheKarten == 0          -6.4044  -8.0721  -4.7367
ExpertIn_schlechteKarten - ExpertIn_durchschnittlicheKarten == 0              -3.7402  -5.4079  -2.0725
ExpertIn_guteKarten - Durchschnitt_guteKarten == 0                            -1.4596  -3.1273   0.2081
Durchschnitt_schlechteKarten - Durchschnitt_guteKarten == 0                   -9.2698 -10.9375  -7.6021
ExpertIn_schlechteKarten - Durchschnitt_guteKarten == 0                       -6.6056  -8.2733  -4.9379
Durchschnitt_schlechteKarten - ExpertIn_guteKarten == 0                       -7.8102  -9.4779  -6.1425
ExpertIn_schlechteKarten - ExpertIn_guteKarten == 0                           -5.1460  -6.8137  -3.4783
ExpertIn_schlechteKarten - Durchschnitt_schlechteKarten == 0                   2.6642   0.9965   4.3319

    6. Erstellen Sie die deskriptiv-statistischen Profilplots mithilfe der Mittelwerte aus den einzelnen Stichproben. Nutzen Sie dafür die Funktion interaction.plot(UV1, UV2, AV). Wenn Sie die Reihenfolge der beiden UVs vertauschen, bekommen Sie den zweiten Profilplot.

      ## Profilplots
interaction.plot(Daten$Koennen, Daten$Glueck, Daten$Geldbetrag_am_Ende)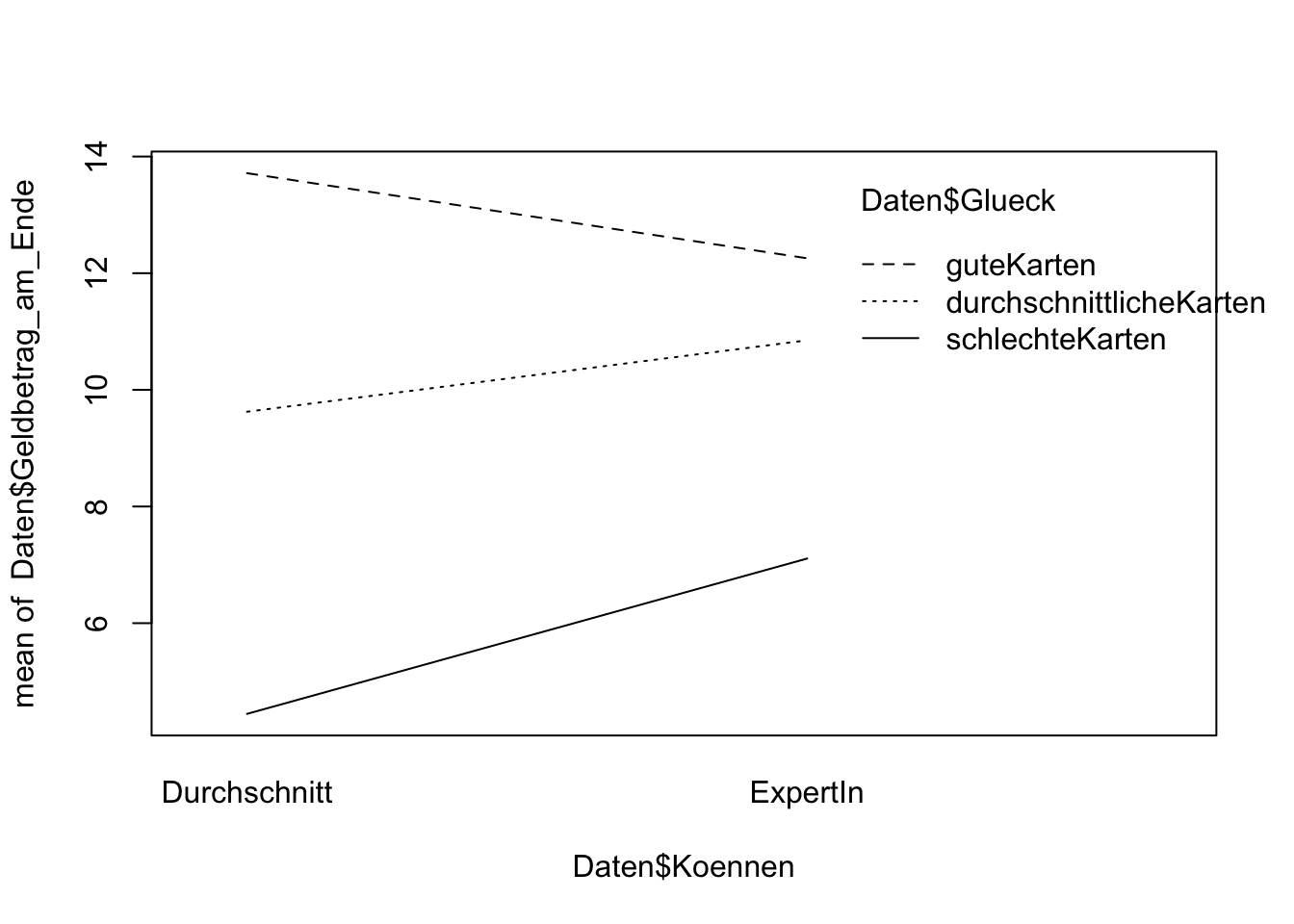

      interaction.plot(Daten$Glueck, Daten$Koennen, Daten$Geldbetrag_am_Ende)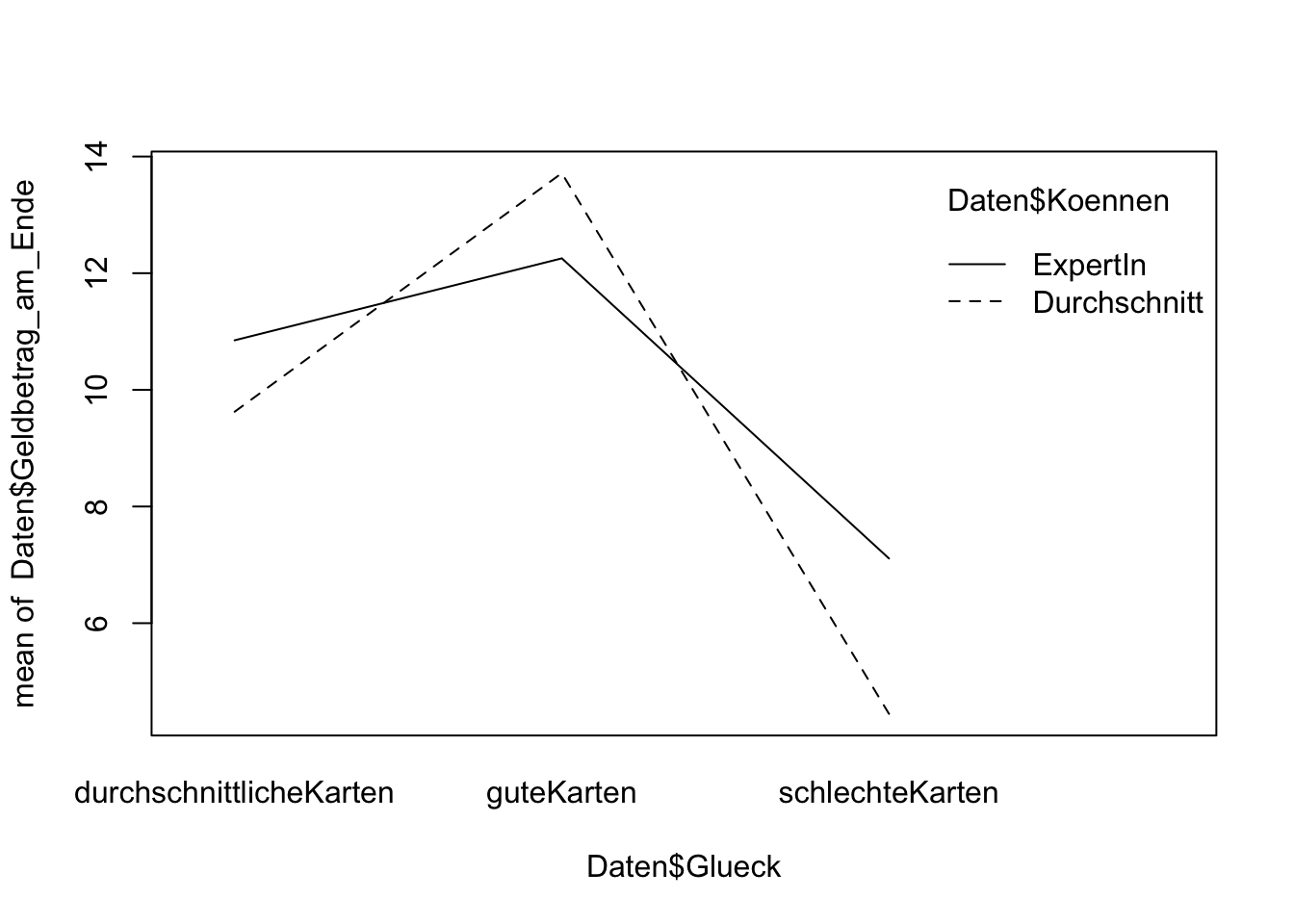

    7. Die Autoren der Studie interpretieren die Ergebnisse bezüglich der Haupteffekte und des Interaktionseffekts so, dass Können beim Pokern keine Rolle spielt. Würden Sie sich dieser Aussage anschließen?

      Da wir davon ausgehen müssen, dass in der Population ein Interaktionseffekt vorliegt, ist eine solche Aussage allein auf Basis der Omnibustests nicht möglich. Schließlich sieht es deskriptiv so aus, als ob Können durchaus eine Rolle spielt: Expertinnen haben deskriptiv bei guten Karten einen niedrigeren mittleren Geldbetrag am Ende als Durchschnittsspielerinnen, wohingegen bei durchschnittlichen oder schlechten Karten der mittlere Geldbetrag bei Expertinnen höher liegt als bei Durchschnittsspielerinnen.

    8. Bonus: Angenommen, Sie interessieren sich dafür, zwischen welchen Gruppen es mittlere Unterschiede gibt. Wie viele Hypothesentests müssten Sie in diesem Fall durchführen?

      Bei einem dreistufigen und einem zweistufigen Faktor, müssten \(\begin{pmatrix}6 \\ 2 \\ \end{pmatrix} = 15\) Hypothesentests durchgeführt werden.

  6. Sie untersuchen, ob der Einfluss der zweistufigen Variable Risikobereitschaft (hoch vs. niedrig) auf die (stetige) Variable Neurotizismus vom Studienfach (Psychologie vs. BWL) abhängt. Die Ergebnisse zeigen sowohl einen Interaktionseffekt als auch einen Haupteffekt Studienfach aber keinen Haupteffekt Risikobereitschaft. Zeichnen Sie in das nachfolgende Profildiagramm die Profillinien so ein, dass diese mit dem Ergebnis der Untersuchung nicht im Widerspruch stehen. Beschriften Sie dabei die x-Achse und die Profillinien und zeichnen Sie auch die Erwartungswerte \(\mu_{j \cdot}\) und \(\mu_{\cdot k}\) ein.

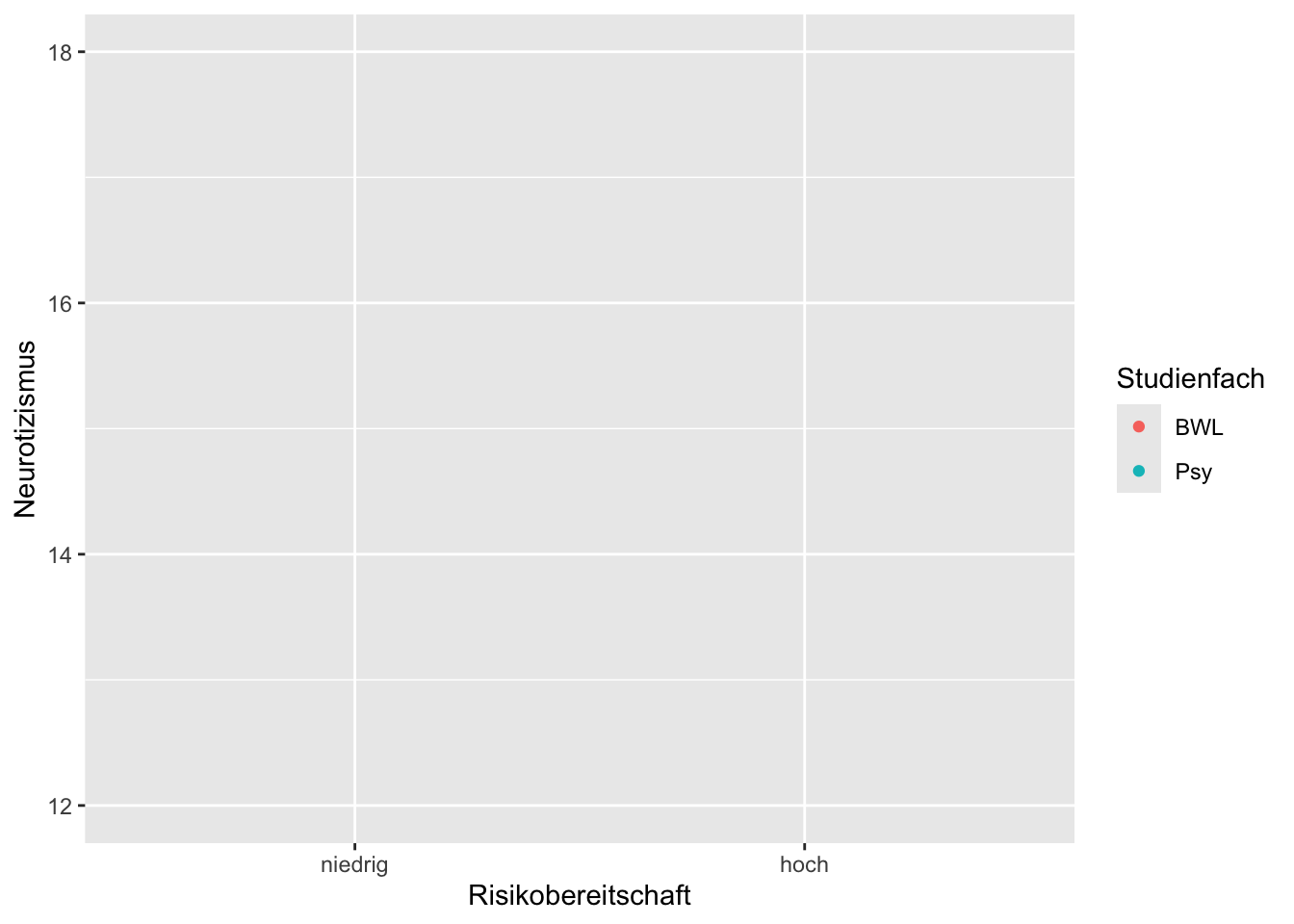
    Erläuterung des oben gezeigten Beispiels:

    Bei dem eingezeichneten Profilplot liegt eine Interaktion von Risikobereitschaft und Studienfach vor, da \(\mu_{n\_ P} - \mu_{h\_ P} \neq \mu_{n\_ B} - \mu_{h\_ B}\) bzw. \(\mu_{n\_ P} - \mu_{n\_ B} \neq \mu_{h\_ P} - \mu_{h\_ B}\). Es liegt ein Haupteffekt Studienfach vor, da \(\mu_{\cdot P} \neq \mu_{\cdot B}\) (damit kann nicht gelten: \(\beta_{P} = \mu_{\cdot P} - \mu = 0 = \mu_{\cdot B} - \mu = \beta_{B}\)). Es liegt kein Haupteffekt Risikobereitschaft vor, da \(\mu_{n \cdot} = \mu_{h \cdot}\) (damit gilt auch: \(\alpha_{n} = \mu_{n \cdot} - \mu = 0 = \alpha_{h} = \mu_{h \cdot} - \mu)\).

    Wichtig: Das ist natürlich nicht die einzige Möglichkeit eines Profilplots mit den gegebenen Anforderungen.

  7. Sie vermuten, dass die Faktoren „Nationalität der Mitarbeiterinnen” (Deutschland, USA) und „Führungsstil” (charismatisch, kooperativ) in ihrem Einfluss auf die Arbeitszufriedenheit der Mitarbeiterinnen auf bestimmte Art und Weise interagieren. Speziell vermuten Sie, dass deutsche Mitarbeiterinnen bei einer kooperativen Führungskraft zufriedener sind als bei einer charismatischen Führungskraft und dass amerikanische Mitarbeiterinnen bei einer charismatischen Führungskraft zufriedener sind als bei einer kooperativen Führungskraft. Hohe Werte stehen dabei für hohe Arbeitszufriedenheit, niedrige Werte für eine niedrige Arbeitszufriedenheit.

    1. Stellen Sie die statistischen Hypothesen auf.

      Einzelne Hypothesen:
      \(H_{01}:\mu_{D\_ k} \leq \mu_{D\_ c}\)
      \(H_{11}:\ \mu_{D\_ k} > \mu_{D\_ c}\)

      \(H_{02}:\mu_{U\_ c} \leq \mu_{U\_ k}\)
      \(H_{12}:\ \mu_{U\_ c} > \mu_{U\_ k}\)

      Zusammengesetzte Hypothesen:
      \(H_{0}:H_{01}\ oder\ H_{02}\)
      \(H_{1}:\ H_{11}\ und\ H_{12}\)

    2. Testen Sie die Hypothesen in R anhand der Datensatzes  (siehe Anleitung oben). Welche Testentscheidungen treffen Sie?

      library(forcats)
library(multcomp)
      ## Daten einlesen
Daten <- read.csv2('Arbeitszufriedenheit.csv', stringsAsFactors = TRUE)
      ## Die beiden Faktoren zu einem Faktor zusammenfassen und zum Datensatz hinzufügen
Daten$Fuehrungsstil_Nationalitaet <- 
  fct_cross(Daten$Fuehrungsstil, Daten$Nationalitaet, sep = '_')
# neue Levels anzeigen
levels(Daten$Fuehrungsstil_Nationalitaet)
      [1] "charismatisch_Deutschland" "kooperativ_Deutschland"    "charismatisch_USA"         "kooperativ_USA"           
      ## Rest wie im einfaktoriellen Modell (nur mit dem kombinierten Faktor)
fit_aov <- aov(Zufriedenheit ~ Fuehrungsstil_Nationalitaet, Daten)
hyp1 <- "kooperativ_Deutschland - charismatisch_Deutschland <= 0"
hyp2 <- "charismatisch_USA - kooperativ_USA <= 0"
hyps <- mcp(Fuehrungsstil_Nationalitaet = c(hyp1, hyp2))
fit <- glht(fit_aov, hyps)
summary(fit, test = univariate()) # unkorrigierte p-Werte
      
  Simultaneous Tests for General Linear Hypotheses

Multiple Comparisons of Means: User-defined Contrasts


Fit: aov(formula = Zufriedenheit ~ Fuehrungsstil_Nationalitaet, data = Daten)

Linear Hypotheses:
                                                        Estimate Std. Error t value Pr(>t)    
kooperativ_Deutschland - charismatisch_Deutschland <= 0  10.2140     0.4108   24.86 <2e-16 ***
charismatisch_USA - kooperativ_USA <= 0                   9.9098     0.4108   24.12 <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Univariate p values reported)

      In beiden Einzelhypothesen Entscheidung für die Alternativhypothese und damit Entscheidung für die zusammengesetzte \(H_{1}\). Man geht davon aus, dass deutsche Mitarbeiterinnen bei einer kooperativen Führungskraft durchschnittlich zufriedener sind als bei einer charismatischen Führungskraft und dass amerikanische Mitarbeiterinnen bei einer charismatischen Führungskraft durchschnittlich zufriedener sind als bei einer kooperativen Führungskraft.

      Da es sich um eine zusammengesetzte Alternativhypothese mit „und” handelt, werden die p-Werte nicht korrigiert.