Übungsblatt 9
Regressionsmodelle mit diskreten Prädiktoren und Interaktionen
Sie interessieren sich für den Einfluss der diskreten UV Vorliegen einer Krebserkrankung auf die stetige AV Depressionsschwere. Als Referenzkategorie wählen Sie die Ausprägung “keine Krebserkrankung” und stellen die folgende Modellgleichung mit Dummy-Variable \(D_{i}\) auf:
\[Y_{i} = \alpha + \beta \cdot D_{i} + \varepsilon_{i}\]
Interpretieren Sie die Parameter \(\alpha\), \(\beta\), \(\alpha + \beta\) und \(- \beta\).
TippLösung\(\alpha\): erwartete Depressionsschwere von Personen ohne Krebserkrankung.
\(\beta\): Differenz der erwarteten Depressionsschwere zwischen Personen mit und ohne Krebserkrankung.
\(\alpha + \beta\): erwartete Depressionsschwere von Personen mit Krebserkrankung.
\(- \beta\): Differenz der erwarteten Depressionsschwere zwischen Personen ohne und mit Krebserkrankung.Sie interessieren sich für den Zusammenhang der diskreten UV Bildungsgrad (Mittelschule (MS), Realschule (RS), Gymnasium(G)) mit der stetigen AV Zufriedenheit. Sie wählen als Referenzkategorie die Ausprägung „Gymnasium” und stellen die folgende Modellgleichung mit Dummy-Variablen \(D_{{MS}_{i}}\) und \(D_{{RS}_{i}}\) auf:
\[Y_{i} = \alpha + \beta_{MS} \cdot D_{{MS}_{i}} + \beta_{RS} \cdot D_{{RS}_{i}} + \varepsilon_{i}\]
Interpretieren Sie die Parameter \(\alpha\), \(\alpha + \beta_{MS}\), \(\alpha{+ \beta}_{RS}\), \(\beta_{MS}\), \(\beta_{RS}\) und \(\beta_{MS} - \ \beta_{RS}\).
TippLösung\(\alpha\): erwartete Zufriedenheit im Gymnasium.
\(\alpha + \beta_{MS}\): erwartete Zufriedenheit in der Mittelschule.
\(\alpha + \beta_{RS}\): erwartete Zufriedenheit in der Realschule.
\(\beta_{MS}\): Differenz der erwarteten Zufriedenheit zwischen Mittelschule und Gymnasium.
\(\beta_{RS}\): Differenz der erwarteten Zufriedenheit zwischen Realschule und Gymnasium.
\(\beta_{MS} - \beta_{RS}\): Differenz der erwarteten Zufriedenheit zwischen Mittelschule und Realschule, da\[\left(\alpha{+ \beta}_{MS} \right) - \left( \alpha{+ \beta}_{RS} \right) = \alpha{+ \beta}_{MS} - \alpha{- \beta}_{RS} = \beta_{MS} - \beta_{RS}\]
Sie wollen untersuchen, inwiefern der Einfluss der (stetigen) UV Intelligenz (z-standardisiert) auf die stetige AV Abiturnote davon abhängt, ob Personen gelernt haben oder nicht. Hierfür wählen Sie als Referenzkategorie die Ausprägung „nicht gelernt” und stellen die folgende Modellgleichung mit Dummy-Variable \(D_{i}\) auf:
\[Y_{i} = \alpha + \beta_{1} \cdot Z_{i} + \beta_{2} \cdot D_{i} + \beta_{3}\left( Z_{i} \cdot D_{i} \right) + \varepsilon_{i}\]
Interpretieren Sie die Parameter \(\alpha\), \(\beta_{1}\), \(\beta_{2}\), \(\beta_{3}\), \(\alpha + \beta_{2}\) und \(\beta_{1} + \beta_{3}\).
TippLösung\(\alpha\): erwartete Abiturnote einer durchschnittlich intelligenten Person, die nicht gelernt hat.
\(\beta_{1}\): Steigungsparameter für den Zusammenhang zwischen Intelligenz und Abiturnote bei Personen, die nicht gelernt haben.
\(\beta_{2}\): Differenz in der erwarteten Abiturnote zwischen durchschnittlich intelligenten Personen, die gelernt haben und durchschnittlich intelligenten Personen, die nicht gelernt haben.
\(\beta_{3}\): Differenz der Steigungsparameter für den Zusammenhang zwischen Intelligenz und Abiturnote zwischen Personen, die gelernt haben, und Personen, die nicht gelernt haben.
\(\alpha + \beta_{2}\): erwartete Abiturnote einer durchschnittlich intelligenten Person, die gelernt hat.
\(\beta_{1} + \beta_{3}\): Steigungsparameter für den Zusammenhang zwischen Intelligenz und Abiturnote bei Personen, die gelernt haben.Sie interessieren sich dafür, inwieweit sich die Mitarbeiter*innen vier verschiedener Unternehmen (BMW, SAP, Allianz, Siemens) in Ihrer mittleren (stetigen) Aggression unterscheiden.
Stellen Sie ein einfaktorielles varianzanalytisches Modell (erste Darstellungsform) für diese Situation auf.
TippLösung\[ Y_{ij} = \mu_{j} + \varepsilon_{ij} \text{ mit } \varepsilon_{ij}\overset{\text{iid}}{\sim} N(0,\sigma^2) \text{ und } j = BMW, SAP, Allianz, Siemens \]
Stellen Sie ein Regressionsmodell mit Dummy-Variablen für diese Situation auf. Wählen Sie Siemens als Referenzkategorie.
TippLösung\[ Y_{i} = \alpha + \beta_{BMW} \cdot D_{{BMW}_{i}} + \beta_{SAP} \cdot D_{{SAP}_{i}} + \beta_{Allianz} \cdot D_{{Allianz}_{i}} + \varepsilon_{i} \text{ mit } \varepsilon_{i}\overset{\text{iid}}{\sim} N(0,\sigma^2) \]
Sie vermuten, dass sich mindestens zwei der Unternehmen in der mittleren Aggression ihrer Mitarbeiter*innen unterscheiden. Stellen Sie sowohl für das varianzanalytische Modell als auch für das Regressionsmodell die geeigneten statistischen Hypothesen auf.
TippLösungVarianzanalytisches Modell:
\(H_{0}:\mu_{BMW} = \mu_{SAP} = \mu_{Allianz} = \mu_{Siemens}\)
\(H_{1}:\mu_{j} \neq \mu_{k}\) für mindestens ein Paar j,kRegressionsmodell:
\(H_{0}:\beta_{BMW} = \beta_{SAP} = \beta_{Allianz} = 0\)
\(H_{1}:\beta_{j} \neq 0\) für mindestens ein j = BMW, SAP, AllianzSie vermuten, dass SAP-Mitarbeiter*innen im Mittel aggressiver als Siemens-Mitarbeiter*innen sind. Stellen Sie sowohl für das varianzanalytische Modell als auch für das Regressionsmodell die statistischen Hypothesen auf.
TippLösungVarianzanalytisches Modell: \[H_{0}:\mu_{SAP} \leq \mu_{Siemens}\] \[H_{1}:\mu_{SAP} > \mu_{Siemens}\]
Regressionsmodell: \[{H_{0}:\beta_{SAP} \leq 0}\] \[{H_{1}:\beta_{SAP} > 0}\]
Sie betrachten ein Regressionsmodell mit einer Dummy-Variable \(D_{i}\), einer stetigen Variable \(X_{i}\) und einem Interaktionsterm:
\[Y_{i} = \alpha + \beta_{1} \cdot X_{i} + \beta_{2} \cdot D_{i} + \beta_{3}\left( X_{i} \cdot D_{i} \right) + \varepsilon_{i}\]
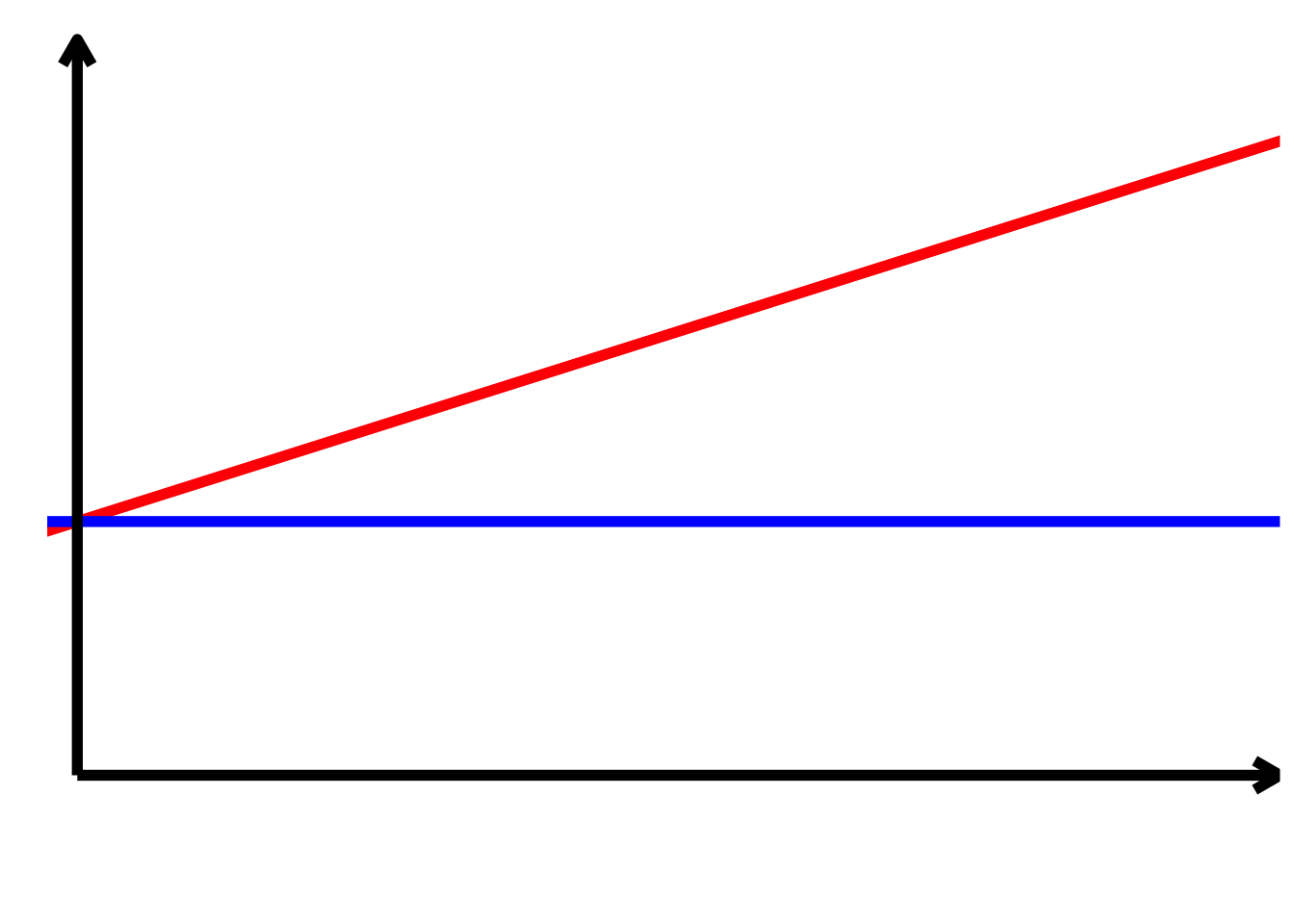
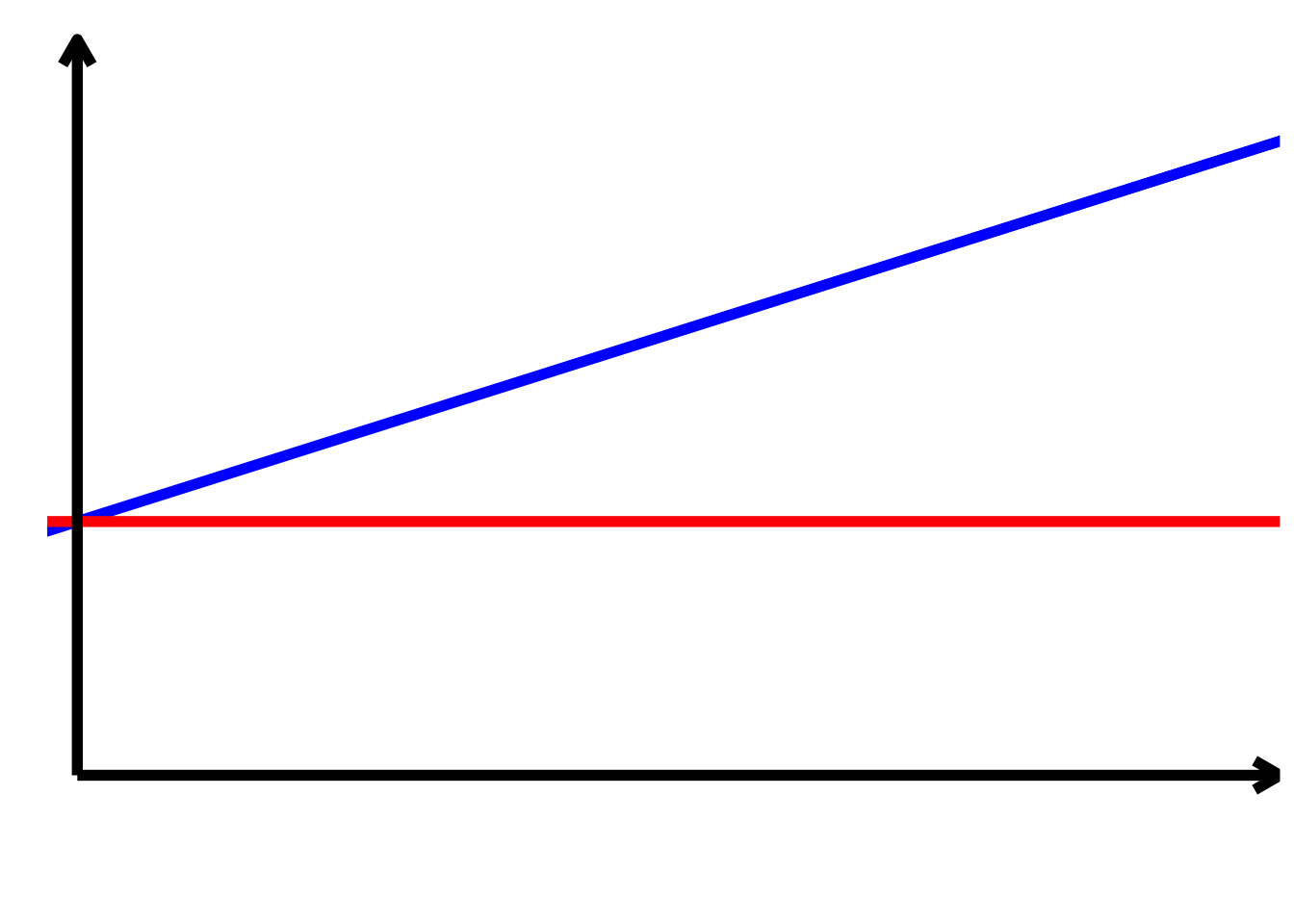
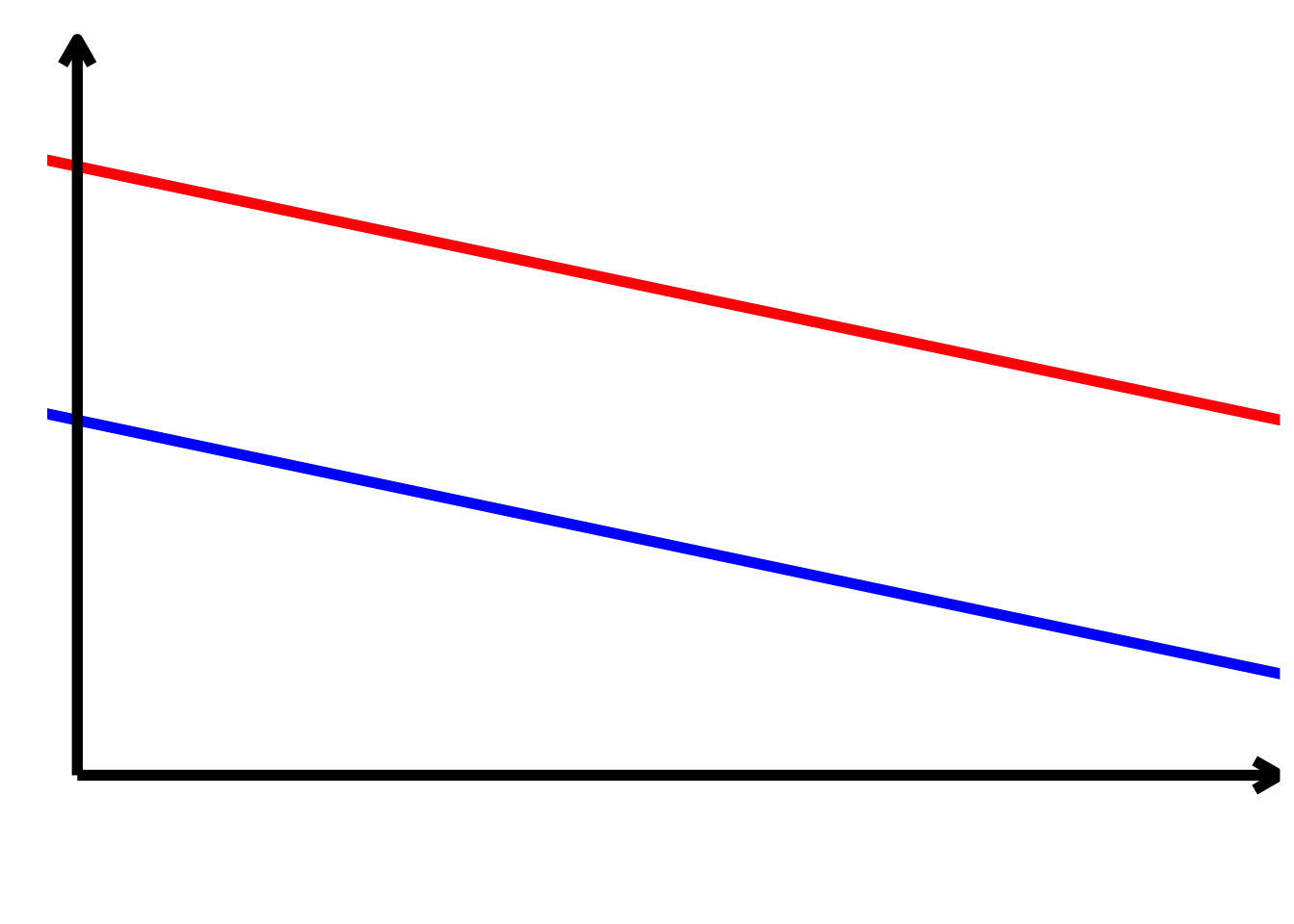
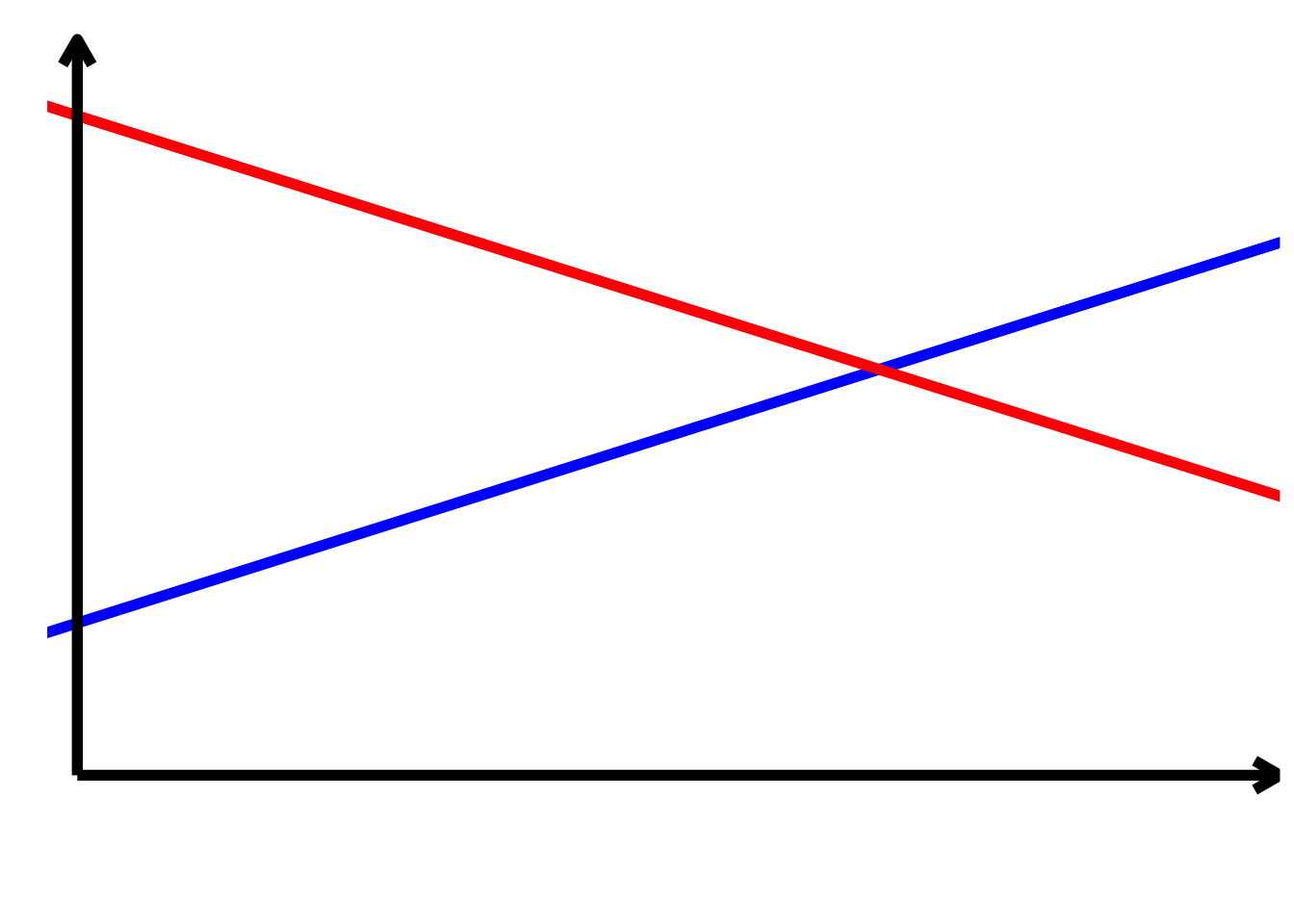
Geben Sie für die folgenden Abbildungen der Regressionsgeraden in den einzelnen Kategorien jeweils an, welche Vorzeichen die Parameter \(\alpha\), \(\alpha + \beta_{2}\), \(\beta_{1}\), \(\beta_{1} + \beta_{3}\), \(\beta_{2}\) und \(\beta_{3}\) haben.
Hinweis 1: Die rote Gerade ist in allen Abbildungen die Regressionsgerade in der Referenzkategorie.
Hinweis 2: Der Schnittpunkt der Achsen ist in allen Abbildungen der Nullpunkt.
TippLösung\[ \begin{align*} \alpha > 0 \\ \alpha + \beta_{2} > 0 \\ \beta_{1} > 0 \\ \beta_{1} + \beta_{3} = 0 \\ \beta_{2} = 0 \\ \beta_{3} < 0 \end{align*} \]
 TippLösung
TippLösung\[ \begin{align*} \alpha > 0 \\ \alpha + \beta_{2} > 0 \\ \beta_{1} = 0 \\ \beta_{1} + \beta_{3} > 0 \\ \beta_{2} = 0 \\ \beta_{3} > 0 \end{align*} \]
 TippLösung
TippLösung\[ \begin{align*} \alpha > 0\\ \alpha + \beta_{2} > 0\\ \beta_{1} < 0\\ \beta_{1} + \beta_{3} < 0\\ \beta_{2} < 0\\ \beta_{3} = 0 \end{align*} \]
 TippLösung
TippLösung\[ \begin{align*} \alpha > 0\\ \alpha + \beta_{2} > 0\\ \beta_{1} < 0\\ \beta_{1} + \beta_{3} > 0\\ \beta_{2} < 0\\ \beta_{3} > 0 \end{align*} \]
 TippLösung
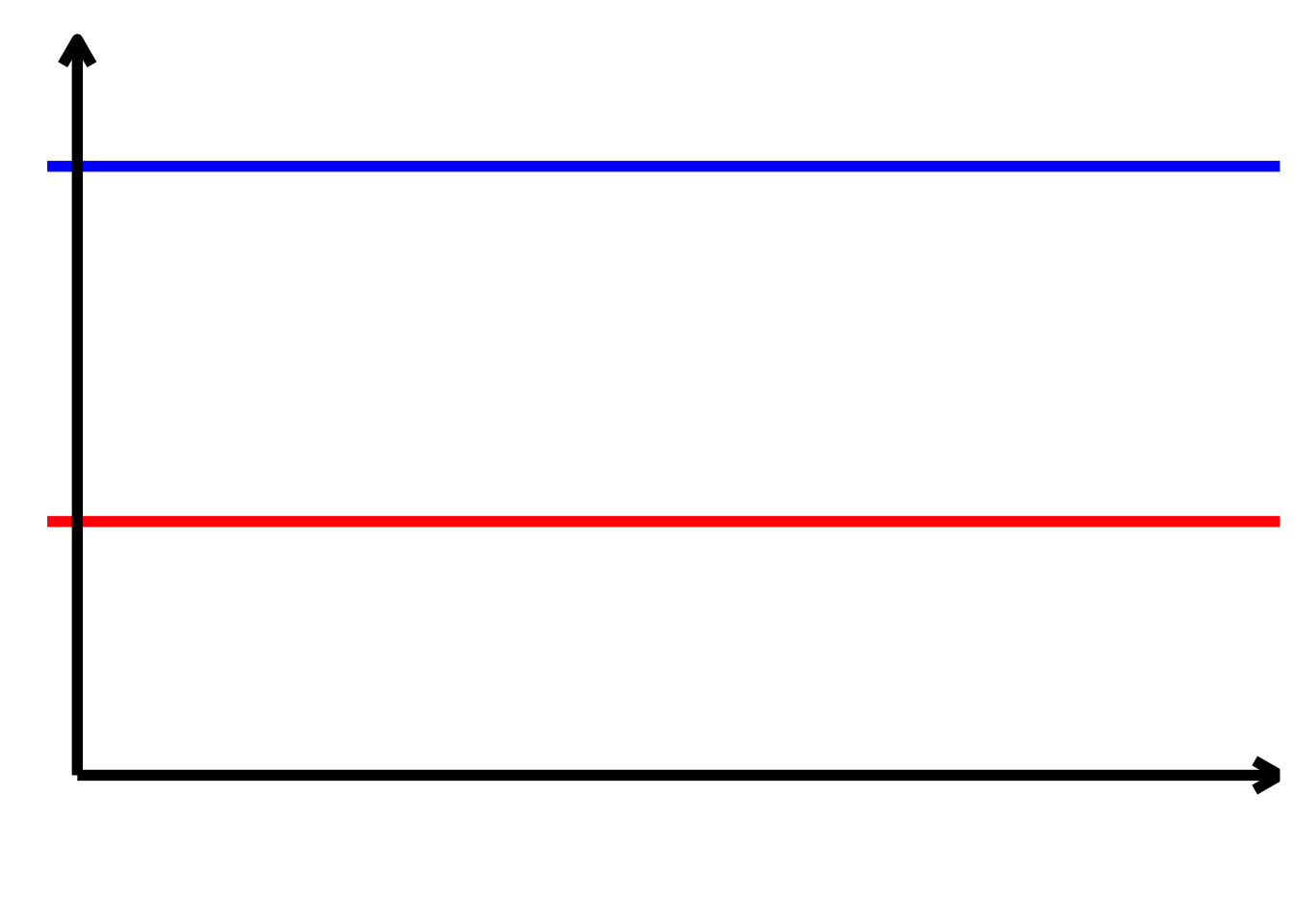
TippLösung\[ \begin{align*} \alpha > 0\\ \alpha + \beta_{2} > 0\\ \beta_{1} = 0\\ \beta_{1} + \beta_{3} = 0\\ \beta_{2} > 0\\ \beta_{3} = 0 \end{align*} \]
 TippLösung
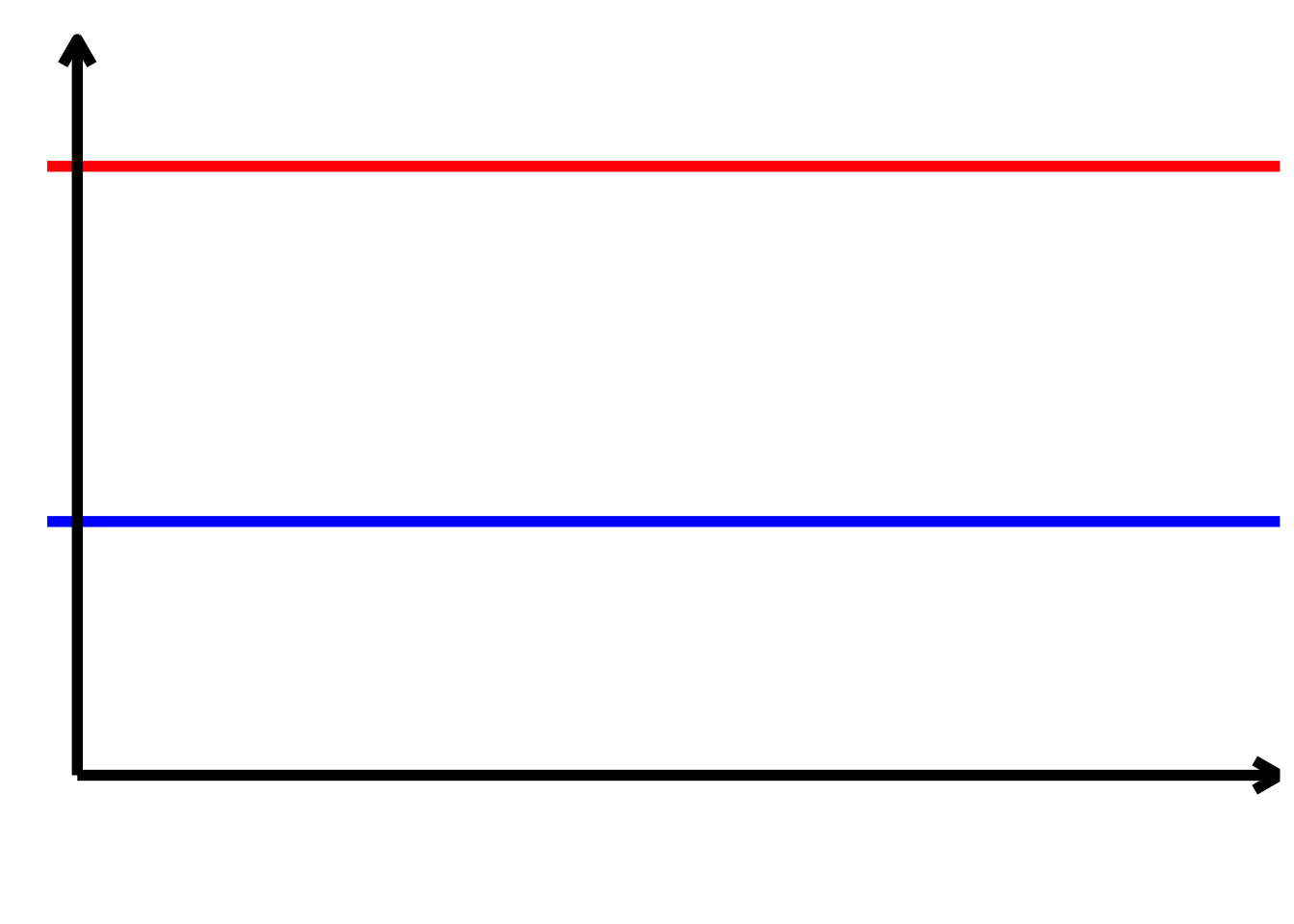
TippLösung\[ \begin{align*} \alpha > 0\\ \alpha + \beta_{2} > 0\\ \beta_{1} = 0\\ \beta_{1} + \beta_{3} = 0\\ \beta_{2} < 0\\ \beta_{3} = 0 \end{align*} \]
 TippLösung
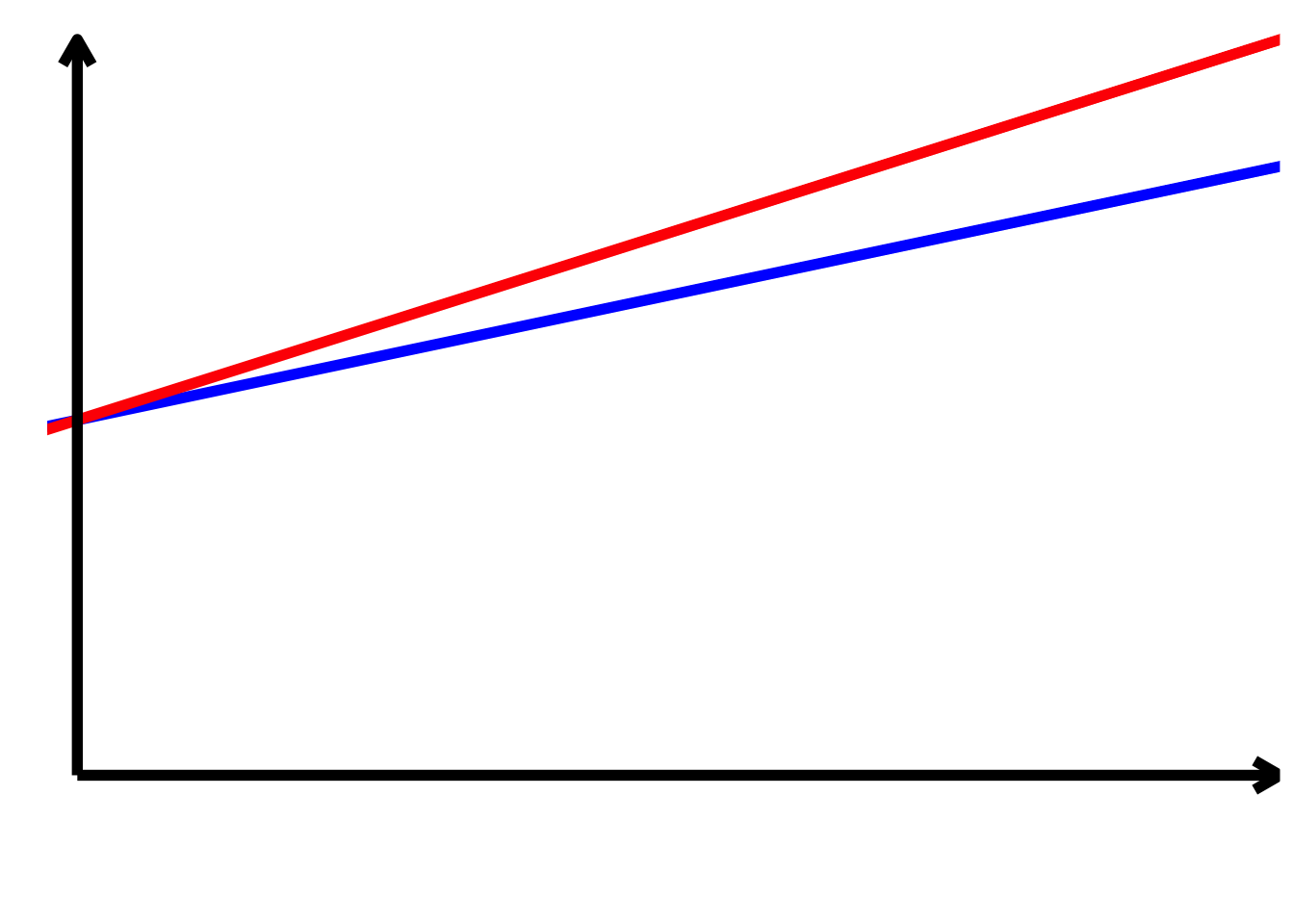
TippLösung\[ \begin{align*} \alpha > 0\\ \alpha + \beta_{2} > 0\\ \beta_{1} > 0\\ \beta_{1} + \beta_{3} > 0\\ \beta_{2} = 0\\ \beta_{3} < 0 \end{align*} \]
 TippLösung
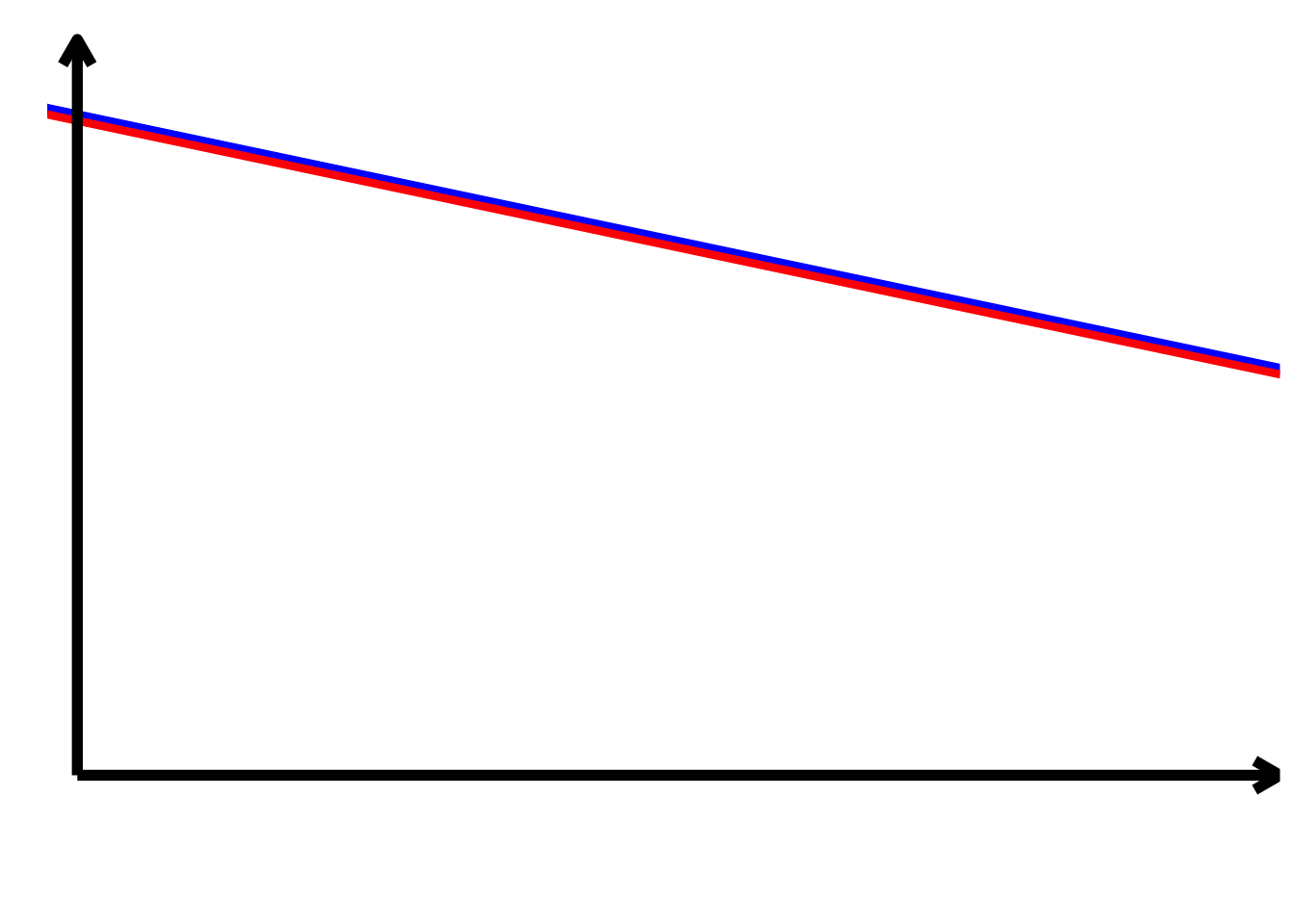
TippLösung\[ \begin{align*} \alpha > 0\\ \alpha + \beta_{2} > 0\\ \beta_{1} < 0\\ \beta_{1} + \beta_{3} < 0\\ \beta_{2} = 0\\ \beta_{3} = 0 \end{align*} \]
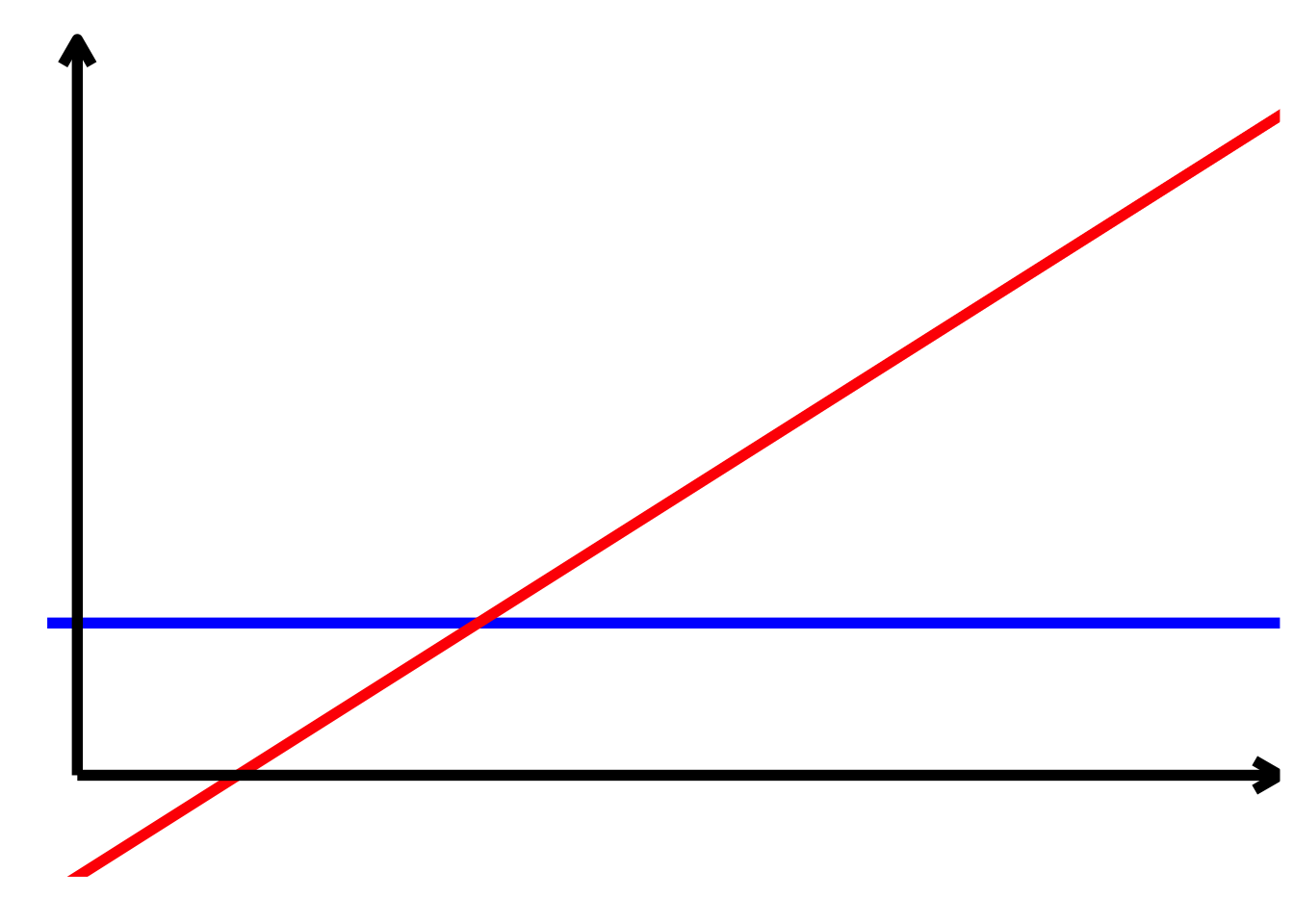 TippLösung
TippLösung\[ \begin{align*} \alpha < 0\\ \alpha + \beta_{2} > 0\\ \beta_{1} > 0\\ \beta_{1} + \beta_{3} = 0\\ \beta_{2} > 0\\ \beta_{3} < 0 \end{align*} \]
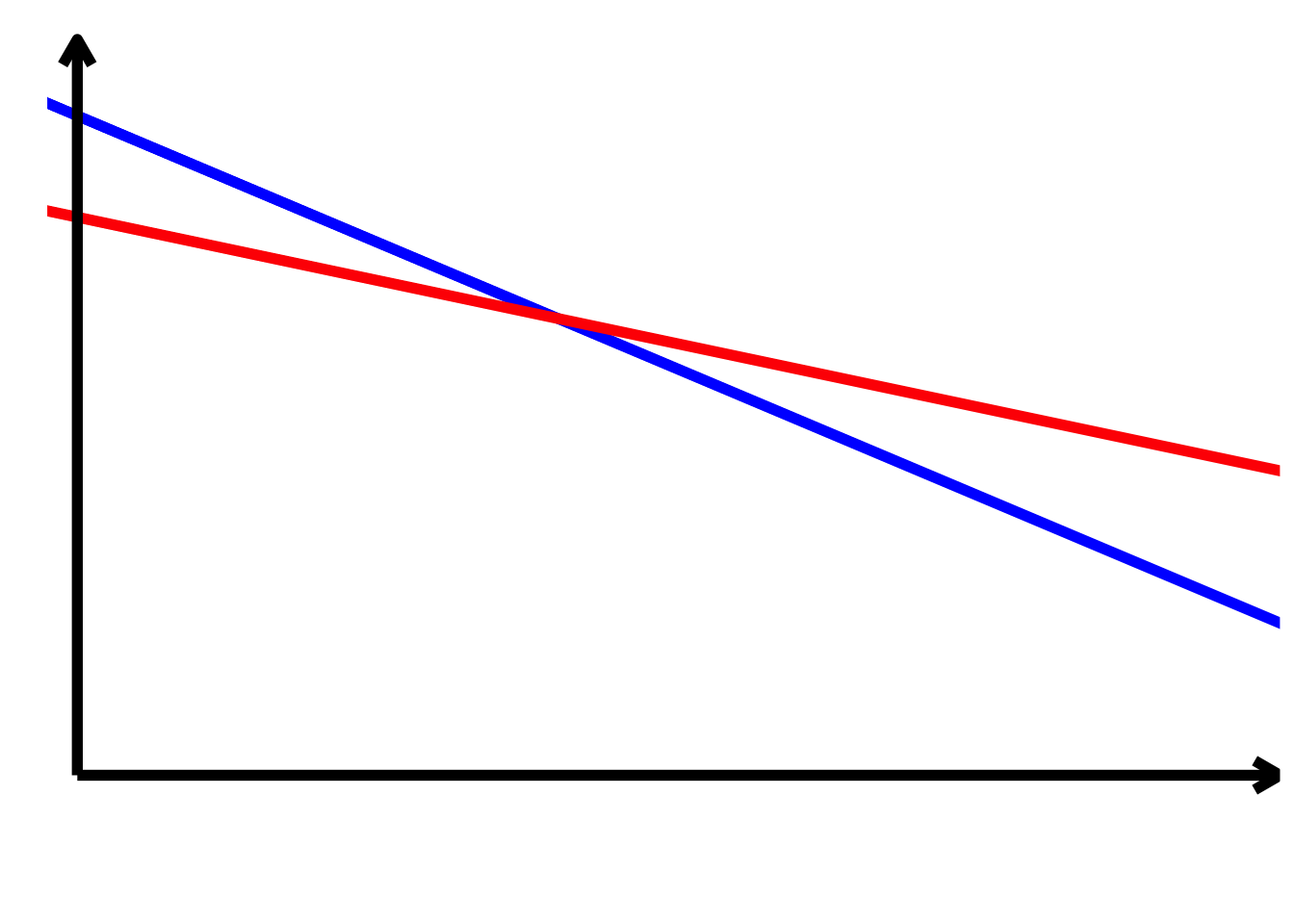 TippLösung
TippLösung\[ \begin{align*} \alpha > 0\\ \alpha + \beta_{2} > 0\\ \beta_{1} < 0\\ \beta_{1} + \beta_{3} < 0\\ \beta_{2} > 0\\ \beta_{3} < 0 \end{align*} \]
Sie wollen den linearen Zusammenhang zwischen der stetigen AV Jahreseinkommen, der stetigen UV Berufspraxis und der diskreten UV Abschluss (Fachhochschule und Hochschule) untersuchen. Als Referenzkategorie für die diskrete UV wählen Sie die Ausprägung „Fachhochschule”.
Stellen Sie die allgemeine Modellgleichung auf.
TippLösung\[Y_{i} = \alpha + \beta_{1} \cdot X_{i} + \beta_{2} \cdot D_{i} + \beta_{3}\left( X_{i} \cdot D_{i} \right) + \varepsilon_{i}\]
Stellen Sie die Modellgleichungen getrennt für die beiden Ausprägungen der diskreten UV auf.
TippLösungFachhochschule: \[Y_{i} = \alpha + \beta_{1} \cdot X_{i} + \varepsilon_{i}\]
Hochschule: \[Y_{i} = (\alpha + \beta_{2}) + (\beta_{1} + \beta_{3}) \cdot X_{i} + \varepsilon_{i}\]
Laden Sie den Datensatz herunter. Die AV Jahreseinkommen ist in diesem Datensatz in Euro, die UV Berufspraxis in Jahren angegeben. Sie wollen überprüfen, ob ein Interaktionseffekt vorliegt. Stellen Sie die statistischen Hypothesen auf und treffen Sie eine Testentscheidung (\(\alpha = 0.005\)).
Hinweis 1: Die Syntax für ein Regressionsmodell mit stetiger UV, diskreter UV und Interaktionsterm ist
lm(AV ~ metrischeUV * diskreteUV, data = Datensatz).Hinweis 2: In R wird automatisch die Kategorie mit dem alphabetisch ersten Anfangsbuchstaben als Referenzkategorie gewählt, in diesem Fall also „Fachhochschule”.
TippLösungStatistische Hypothesen: \[ \begin{align*} H_{0}:\beta_{3} = 0 \\ H_{1}:\beta_{3} \neq 0 \end{align*} \]
Hypothesentest:
## Daten einlesen daten <- read.csv2('Einkommen.csv', stringsAsFactors = TRUE)## lm-Objekt erstellen fit <- lm(Einkommen ~ Berufspraxis * Abschluss, data = daten) ## Punktschätzwerte und Hypothesentests summary(fit)Call: lm(formula = Einkommen ~ Berufspraxis * Abschluss, data = daten) Residuals: Min 1Q Median 3Q Max -36571 -2541 -26 3082 28570 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -21636.4 2143.0 -10.096 < 2e-16 *** Berufspraxis 4636.3 167.4 27.692 < 2e-16 *** AbschlussHochschule -19440.7 3099.0 -6.273 1.25e-09 *** Berufspraxis:AbschlussHochschule 3475.0 238.5 14.567 < 2e-16 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 6540 on 296 degrees of freedom Multiple R-squared: 0.9357, Adjusted R-squared: 0.9351 F-statistic: 1437 on 3 and 296 DF, p-value: < 2.2e-16Der p-Wert ist mit < 0.0000000000000002 kleiner als \(\alpha = 0.005\). Wir entscheiden uns daher für die \(H_{1}:\beta_{3} \neq 0\) und somit dafür, dass ein Interaktionseffekt vorliegt.
Z-standardisieren Sie die Variable Berufspraxis und schätzen Sie das statistische Regressionsmodell erneut. Berechnen Sie 95%-KIs für die Parameter \(\alpha\), \(\beta_{1}\), \(\beta_{2}\) und \(\beta_{3}\) im Modell mit z-standardisierter Berufspraxis und interpretieren Sie diese.
TippLösung## lm-Objekt mit z-Standardisierung der UV Berufspraxis fit_z <- lm(Einkommen ~ scale(Berufspraxis) * Abschluss, data = daten) ## Konfidenzintervalle für das Modell mit z-standardisierter Berufspraxis confint(fit_z)2.5 % 97.5 % (Intercept) 35705.515 37811.31 scale(Berufspraxis) 13684.941 15778.84 AbschlussHochschule 22837.598 25815.73 scale(Berufspraxis):AbschlussHochschule 9549.944 12533.38KI für \(\alpha\): Wir gehen davon aus, dass das durchschnittliche Jahreseinkommen von Personen mit Fachhochschulabschluss und durchschnittlicher Berufspraxis zwischen 35705.515 und 37811.31 Euro liegt.
KI für \(\beta_{1}\): Wir gehen davon aus, dass das durchschnittliche Jahreseinkommen von Personen mit Fachhochschulabschluss um 13684.941 bis 15778.84 Euro steigt, wenn die Berufspraxis um eine Standardabweichung steigt.
KI für \(\beta_{2}\): Wir gehen davon aus, dass das durchschnittliche Jahreseinkommen von Personen mit Hochschulabschluss und durchschnittlicher Berufserfahrung 22837.598 bis 25815.73 Euro höher ist als das durchschnittliche Jahreseinkommen von Personen mit Fachhochschulabschluss und durchschnittlicher Berufserfahrung.
KI für \(\beta_{3}\): Wir gehen davon aus, dass das die Steigung des durchschnittlichen Jahreseinkommens pro Steigung der Berufspraxis um eine Standardabweichung bei Personen mit Hochschulabschluss um 9549.944 bis 12533.38 Euro höher ist als bei Personen mit Fachhochschulabschluss.
Sie wollen mithilfe des Datensatzes aus Aufgabe 6 überprüfen, ob es für mindestens einen der beiden Abschlüsse (Fachhochschule oder Hochschule) einen positiven Zusammenhang zwischen der Berufspraxis und dem Jahreseinkommen gibt.
Stellen Sie die zusammengesetzten Hypothesen für diese Fragestellung auf und begründen Sie, ob eine Korrektur der p-Werte notwendig ist.
TippLösungAllgemeine Modellgleichung:
\[Y_{i} = \alpha + \beta_{1} \cdot X_{i} + \beta_{2} \cdot D_{i} + \beta_{3}\left( X_{i} \cdot D_{i} \right) + \varepsilon_{i}\]
Hypothesen: \[H_{0}:\ \beta_{1} \leq 0\ und\ \beta_{1} + \beta_{3} \leq 0\] \[H_{1}:\ \beta_{1} > 0\ oder\ \beta_{1} + \beta_{3} > 0\]
Da es sich um eine zusammengesetzte Alternativhypothese mit „oder” handelt, müssen die p-Werte für die Überprüfung der zusammengesetzten Hypothesen korrigiert werden.
Berechnen Sie die unkorrigierten p-Werte für die einzelnen Hypothesentests mithilfe der glht Funktion aus dem multcomp package.
HinweisVerwendung des multcomp-Pakets## Mithilfe der glht Funktion aus dem multcomp package können ## Konfidenzintervalle und (beliebige) Hypothesentests für Parameter(-kombinationen) ## linearer (und auch logistischer) Regressionsmodelle berechnet werden. ## Die Syntax ist aehnlich wie in den varianzanalytischen Modellen: ## 1) Erstellen eines lm-Objekts z.B. mit dem Namen fit_lm ## 2) Definition der Parameter bzw. der Nullhypothesen als character-Vektor ## und Speichern dieses Vektors als Objekt z.B. mit dem Namen hyps ## 3) fit <- glht(fit_lm, hyps) ## 4) summary(fit, test=univariate()) für unkorrigierte Hypothesentests ## confint(fit, calpha = univariate_calpha()) für Konfidenzintervalle ## Genau wie bei den varianzanalytischen Modellen muessen Sie für ## Konfidenzintervalle eine ungerichtete Nullhypothese der Form ## 'Modellparameter == 0' definieren. ## Im Unterschied zu den varianzanalytischen Modellen können ## Sie die character-Vektoren direkt der glht-Funktion übergeben. ## Sie brauchen die mcp-Funktion hier also nicht. ## Die für die Erstellung des character-Vektors benötigten ## Parameternamen können Sie dabei dem Output von summary(fit_lm) entnehmen ## Beispiel I: Gerichtete Hypothesentests für den Parameter eines Interaktionseffekts: library(multcomp) fit_lm <- lm(AV ~ UV1 * UV2, data = daten) hyp <- "UV1:UV2 <= 0" fit_glht <- glht(fit_lm, hyp) summary(fit_glht, test=univariate())TippLösunglibrary(multcomp) ## Daten einlesen daten <- read.csv2('data/Einkommen.csv', stringsAsFactors = TRUE) ## lm Objekt erstellen fit_lm <- lm(Einkommen ~ Berufspraxis * Abschluss, data = daten) ## Nullhypothesen definieren hyps <- c('Berufspraxis <= 0', 'Berufspraxis + Berufspraxis:AbschlussHochschule <= 0') ## glht Obkjekt erstellen fit <- glht(fit_lm, hyps) ## unkorrigierte p-Werte summary(fit, test = univariate())Simultaneous Tests for General Linear Hypotheses Fit: lm(formula = Einkommen ~ Berufspraxis * Abschluss, data = daten) Linear Hypotheses: Estimate Std. Error t value Pr(>t) Berufspraxis <= 0 4636.3 167.4 27.69 <2e-16 *** Berufspraxis + Berufspraxis:AbschlussHochschule <= 0 8111.3 169.9 47.73 <2e-16 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 (Univariate p values reported)Welche Korrekturmethode würden Sie in diesem Fall wählen? Treffen Sie auf Basis dieser Korrekturmethode eine Testentscheidung für die zusammengesetzten Hypothesen (\(\alpha^{*} = 0.005\)).
TippLösungDa wir die Hypothesen im Rahmen der multiplen linearen Regression untersuchen, können wir hier die Tukey-Methode verwenden. Der auf ihr basierende Test hat eine höhere Power als bei einer Korrektur mit der Bonferroni-Methode.
## Tukey-korrigierte p-Werte summary(fit, test = adjusted('single-step'))Simultaneous Tests for General Linear Hypotheses Fit: lm(formula = Einkommen ~ Berufspraxis * Abschluss, data = daten) Linear Hypotheses: Estimate Std. Error t value Pr(>t) Berufspraxis <= 0 4636.3 167.4 27.69 <1e-10 *** Berufspraxis + Berufspraxis:AbschlussHochschule <= 0 8111.3 169.9 47.73 <1e-10 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 (Adjusted p values reported -- single-step method)Da die Tukey-korrigierten p-Werte beide kleiner als 0.005 sind, entscheiden wir uns für die zusammengesetzte Alternativhypothese.