Gemischte Lineare Modelle mit R

Veröffentlichungsdatum

12. März 2025

Teil 1

Intro

Als erstes brauchen wir erst mal Daten. Laden Sie sich den Datensatz HSB.csv hier herunter und verschieben Sie die Datei in Ihren Projektordner (eventuell erstellen Sie für das Thema LMMs ein neues RStudio Projekt. Öffnen Sie danach RStudio, indem Sie auf die .Rproj Verknüpfung Ihres Projekts doppelklicken. Lesen Sie dann den Datensatz in R ein.

hsb <- read.csv2("HSB.csv")

Dann schauen wir als erstes, wie der Datensatz überhaupt ausschaut und welche Variablen da drin sind.

head(hsb)

  School Minority    Sex   SES MathAch Size Sector PRACAD DISCLIM MeanSES
1   1224       No Female -1.53    5.88  842 Public   0.35     1.6   -0.43
2   1224       No Female -0.59   19.71  842 Public   0.35     1.6   -0.43
3   1224       No   Male -0.53   20.35  842 Public   0.35     1.6   -0.43
4   1224       No   Male -0.67    8.78  842 Public   0.35     1.6   -0.43
5   1224       No   Male -0.16   17.90  842 Public   0.35     1.6   -0.43
6   1224       No   Male  0.02    4.58  842 Public   0.35     1.6   -0.43

Wir haben also offenbar eine Variable die die Zugehörigkeit zur Schule angibt (School), dann die L1-Variablen Minority, Sex, SES und MathAch (selbsterklärend), dann kommen die L2-Variablen Size, Sector (Public oder Catholic), PRACAD (wie viele % sind auf dem “Academic Track”), DISCLIM, und MeanSES.

Als Abhängige Variable interessiert uns vornehmlich MathAch. Wenn wir also wissen wollen, ob die durchschnittliche Mathematiknote in den einzelnen Schulen unterschiedlich ist, können wir einfach mal ein lineares Modell rechnen mit MathAch als abhängige Variable und School als Prädiktor. Dabei wollen wir keinen Intercept und School als factor kodiert als einzigen Prädiktor. Bei insgesamt 160 Schulen im Datensatz führt diese Lösung dazu, dass für jede Schule eine dichotome Variable (Dummyvariable) im Modell erstellt wird, wobei gilt: \[ x_j = \begin{cases} 1 \text{, falls Schule = j und} \\ 0 \text{, für alle anderen Schulen.} \end{cases} \] Wir erhalten also für jede dieser k = 160 neuen Variablen eine Schätzung im Modell, die dem Intercept für jeweils genau eine Schule j entspricht (mit 0 + in der lm-Syntax kann man den Gesamtintercept im Modell weglassen).

model1 <- lm(formula = MathAch ~ 0 + as.factor(School), data = hsb)
summary(model1)


Call:
lm(formula = MathAch ~ 0 + as.factor(School), data = hsb)

Residuals:
     Min       1Q   Median       3Q      Max 
-19.6733  -4.6173   0.1573   4.6719  17.9663 

Coefficients:
                      Estimate Std. Error t value Pr(>|t|)    
as.factor(School)1224   9.7162     0.9126  10.647  < 2e-16 ***
as.factor(School)1288  13.5112     1.2513  10.798  < 2e-16 ***
as.factor(School)1296   7.6369     0.9030   8.457  < 2e-16 ***
as.factor(School)1308  16.2560     1.3989  11.620  < 2e-16 ***
as.factor(School)1317  13.1781     0.9030  14.593  < 2e-16 ***
as.factor(School)1358  11.2063     1.1422   9.811  < 2e-16 ***
as.factor(School)1374   9.7275     1.1823   8.227 2.26e-16 ***
as.factor(School)1433  19.7189     1.0575  18.647  < 2e-16 ***
as.factor(School)1436  18.1120     0.9432  19.203  < 2e-16 ***
as.factor(School)1461  16.8433     1.0891  15.466  < 2e-16 ***
as.factor(School)1462  10.4960     0.8287  12.666  < 2e-16 ***
as.factor(School)1477  14.2294     0.7945  17.909  < 2e-16 ***
as.factor(School)1499   7.6609     0.8594   8.915  < 2e-16 ***
as.factor(School)1637   7.0237     1.2040   5.834 5.67e-09 ***
as.factor(School)1906  15.9843     0.8594  18.600  < 2e-16 ***
as.factor(School)1909  14.4246     1.1823  12.200  < 2e-16 ***
as.factor(School)1942  18.1110     1.1618  15.589  < 2e-16 ***
as.factor(School)1946  12.9087     1.0018  12.885  < 2e-16 ***
as.factor(School)2030  12.0787     0.9126  13.236  < 2e-16 ***
as.factor(School)2208  15.4058     0.8077  19.074  < 2e-16 ***
as.factor(School)2277   9.2982     0.8010  11.608  < 2e-16 ***
as.factor(School)2305  11.1379     0.7643  14.572  < 2e-16 ***
as.factor(School)2336  16.5181     0.9126  18.101  < 2e-16 ***
as.factor(School)2458  13.9861     0.8287  16.878  < 2e-16 ***
as.factor(School)2467  10.1483     0.8676  11.697  < 2e-16 ***
as.factor(School)2526  17.0530     0.8287  20.579  < 2e-16 ***
as.factor(School)2626  13.3971     1.0149  13.200  < 2e-16 ***
as.factor(School)2629  14.9084     0.8287  17.991  < 2e-16 ***
as.factor(School)2639   6.6171     0.9654   6.855 7.76e-12 ***
as.factor(School)2651  11.0853     1.0149  10.922  < 2e-16 ***
as.factor(School)2655  12.3456     0.8676  14.230  < 2e-16 ***
as.factor(School)2658  13.3964     0.9326  14.364  < 2e-16 ***
as.factor(School)2755  16.4770     0.9126  18.056  < 2e-16 ***
as.factor(School)2768  10.8876     1.2513   8.701  < 2e-16 ***
as.factor(School)2771  11.8445     0.8436  14.041  < 2e-16 ***
as.factor(School)2818  13.8743     0.9654  14.372  < 2e-16 ***
as.factor(School)2917   7.9793     0.9541   8.363  < 2e-16 ***
as.factor(School)2990  18.4488     0.9030  20.430  < 2e-16 ***
as.factor(School)2995   9.5472     0.9224  10.350  < 2e-16 ***
as.factor(School)3013  12.6115     0.8594  14.675  < 2e-16 ***
as.factor(School)3020  14.3963     0.8145  17.675  < 2e-16 ***
as.factor(School)3039  16.9652     1.3652  12.427  < 2e-16 ***
as.factor(School)3088   9.1464     1.0018   9.130  < 2e-16 ***
as.factor(School)3152  13.2085     0.8676  15.224  < 2e-16 ***
as.factor(School)3332  14.2784     1.0149  14.069  < 2e-16 ***
as.factor(School)3351  11.4654     1.0018  11.445  < 2e-16 ***
as.factor(School)3377   9.1876     0.9326   9.851  < 2e-16 ***
as.factor(School)3427  19.7153     0.8938  22.059  < 2e-16 ***
as.factor(School)3498  16.3913     0.8594  19.074  < 2e-16 ***
as.factor(School)3499  13.2771     1.0149  13.082  < 2e-16 ***
as.factor(School)3533  10.4094     0.9030  11.527  < 2e-16 ***
as.factor(School)3610  15.3552     0.7820  19.635  < 2e-16 ***
as.factor(School)3657   9.5212     0.8761  10.868  < 2e-16 ***
as.factor(School)3688  14.6567     0.9541  15.362  < 2e-16 ***
as.factor(School)3705  10.3322     0.9326  11.079  < 2e-16 ***
as.factor(School)3716  10.3688     0.9771  10.612  < 2e-16 ***
as.factor(School)3838  16.0633     0.8514  18.868  < 2e-16 ***
as.factor(School)3881  11.9500     0.9771  12.230  < 2e-16 ***
as.factor(School)3967  12.0352     0.8676  13.872  < 2e-16 ***
as.factor(School)3992  14.6460     0.8594  17.043  < 2e-16 ***
as.factor(School)3999  10.9446     0.9224  11.865  < 2e-16 ***
as.factor(School)4042  14.3161     0.7820  18.306  < 2e-16 ***
as.factor(School)4173  12.7255     0.9432  13.492  < 2e-16 ***
as.factor(School)4223  14.6227     0.9326  15.679  < 2e-16 ***
as.factor(School)4253   9.4131     0.8215  11.459  < 2e-16 ***
as.factor(School)4292  12.8646     0.7760  16.578  < 2e-16 ***
as.factor(School)4325  13.2398     0.8594  15.406  < 2e-16 ***
as.factor(School)4350  11.8555     1.0891  10.886  < 2e-16 ***
as.factor(School)4383  11.4660     1.2513   9.164  < 2e-16 ***
as.factor(School)4410  13.4734     0.9771  13.790  < 2e-16 ***
as.factor(School)4420  13.8753     1.1060  12.546  < 2e-16 ***
as.factor(School)4458   5.8117     0.9030   6.436 1.31e-10 ***
as.factor(School)4511  13.4093     0.8215  16.323  < 2e-16 ***
as.factor(School)4523   8.3517     0.9126   9.152  < 2e-16 ***
as.factor(School)4530   9.0563     0.7882  11.490  < 2e-16 ***
as.factor(School)4642  14.5993     0.8010  18.226  < 2e-16 ***
as.factor(School)4868  12.3103     1.0729  11.473  < 2e-16 ***
as.factor(School)4931  13.7917     0.8215  16.789  < 2e-16 ***
as.factor(School)5192  10.4093     1.1823   8.804  < 2e-16 ***
as.factor(School)5404  15.4156     0.8287  18.603  < 2e-16 ***
as.factor(School)5619  15.4170     0.7701  20.020  < 2e-16 ***
as.factor(School)5640  13.1612     0.8287  15.882  < 2e-16 ***
as.factor(School)5650  14.2742     0.9326  15.305  < 2e-16 ***
as.factor(School)5667  13.7782     0.8010  17.200  < 2e-16 ***
as.factor(School)5720  14.2830     0.8594  16.620  < 2e-16 ***
as.factor(School)5761  11.1375     0.8676  12.837  < 2e-16 ***
as.factor(School)5762   4.3246     1.0285   4.205 2.65e-05 ***
as.factor(School)5783  13.1510     1.1618  11.320  < 2e-16 ***
as.factor(School)5815   7.2716     1.2513   5.811 6.46e-09 ***
as.factor(School)5819  12.1396     0.8848  13.721  < 2e-16 ***
as.factor(School)5838  13.6903     1.1237  12.184  < 2e-16 ***
as.factor(School)5937  16.7759     1.1618  14.440  < 2e-16 ***
as.factor(School)6074  13.7791     0.8360  16.482  < 2e-16 ***
as.factor(School)6089  15.5697     1.0891  14.296  < 2e-16 ***
as.factor(School)6144   8.5458     0.9541   8.957  < 2e-16 ***
as.factor(School)6170  14.1814     1.3652  10.388  < 2e-16 ***
as.factor(School)6291  10.1077     1.0575   9.558  < 2e-16 ***
as.factor(School)6366  15.6569     0.8215  19.059  < 2e-16 ***
as.factor(School)6397  12.7965     0.8077  15.843  < 2e-16 ***
as.factor(School)6415  11.8613     0.8514  13.932  < 2e-16 ***
as.factor(School)6443   9.4760     1.1422   8.296  < 2e-16 ***
as.factor(School)6464   7.0924     1.1618   6.105 1.08e-09 ***
as.factor(School)6469  18.4554     0.8287  22.271  < 2e-16 ***
as.factor(School)6484  12.9120     1.0575  12.210  < 2e-16 ***
as.factor(School)6578  11.9945     0.8360  14.347  < 2e-16 ***
as.factor(School)6600  11.7045     0.8360  14.000  < 2e-16 ***
as.factor(School)6808   9.2864     0.9432   9.846  < 2e-16 ***
as.factor(School)6816  14.5380     0.8436  17.233  < 2e-16 ***
as.factor(School)6897  15.0978     0.8938  16.893  < 2e-16 ***
as.factor(School)6990   5.9777     0.8594   6.956 3.82e-12 ***
as.factor(School)7011  13.8133     1.0891  12.684  < 2e-16 ***
as.factor(School)7101  11.8500     1.1823  10.023  < 2e-16 ***
as.factor(School)7172   8.0673     0.9432   8.553  < 2e-16 ***
as.factor(School)7232  12.5429     0.8676  14.457  < 2e-16 ***
as.factor(School)7276  12.6802     0.8594  14.755  < 2e-16 ***
as.factor(School)7332  14.6365     0.9030  16.208  < 2e-16 ***
as.factor(School)7341   9.7951     0.8761  11.181  < 2e-16 ***
as.factor(School)7342  11.1667     0.8215  13.593  < 2e-16 ***
as.factor(School)7345  11.3391     0.8360  13.563  < 2e-16 ***
as.factor(School)7364  14.1732     0.9432  15.027  < 2e-16 ***
as.factor(School)7635  15.0663     0.8761  17.198  < 2e-16 ***
as.factor(School)7688  18.4231     0.8514  21.639  < 2e-16 ***
as.factor(School)7697  15.7228     1.1060  14.216  < 2e-16 ***
as.factor(School)7734  10.5586     1.3338   7.916 2.83e-15 ***
as.factor(School)7890   8.3412     0.8761   9.521  < 2e-16 ***
as.factor(School)7919  14.8508     1.0285  14.439  < 2e-16 ***
as.factor(School)8009  14.0849     0.9126  15.434  < 2e-16 ***
as.factor(School)8150  14.8532     0.9432  15.748  < 2e-16 ***
as.factor(School)8165  16.4520     0.8938  18.408  < 2e-16 ***
as.factor(School)8175  11.6982     1.0891  10.741  < 2e-16 ***
as.factor(School)8188  12.7420     1.1422  11.155  < 2e-16 ***
as.factor(School)8193  16.2323     0.9541  17.014  < 2e-16 ***
as.factor(School)8202  11.7137     1.0575  11.077  < 2e-16 ***
as.factor(School)8357  14.3822     1.2040  11.945  < 2e-16 ***
as.factor(School)8367   4.5550     1.6721   2.724 0.006462 ** 
as.factor(School)8477  12.5227     1.0285  12.175  < 2e-16 ***
as.factor(School)8531  13.5295     0.9771  13.847  < 2e-16 ***
as.factor(School)8627  10.8840     0.8594  12.665  < 2e-16 ***
as.factor(School)8628  16.5289     0.8010  20.634  < 2e-16 ***
as.factor(School)8707  12.8846     0.9030  14.268  < 2e-16 ***
as.factor(School)8775   9.4683     0.9030  10.485  < 2e-16 ***
as.factor(School)8800   7.3369     1.1060   6.634 3.51e-11 ***
as.factor(School)8854   4.2400     1.1060   3.834 0.000127 ***
as.factor(School)8857  15.2973     0.7820  19.561  < 2e-16 ***
as.factor(School)8874  12.0547     1.0427  11.561  < 2e-16 ***
as.factor(School)8946  10.3752     0.8215  12.630  < 2e-16 ***
as.factor(School)8983  10.9922     0.8761  12.547  < 2e-16 ***
as.factor(School)9021  14.6973     0.8360  17.580  < 2e-16 ***
as.factor(School)9104  16.8322     0.8436  19.953  < 2e-16 ***
as.factor(School)9158   8.5458     0.8594   9.944  < 2e-16 ***
as.factor(School)9198  19.0932     1.1237  16.992  < 2e-16 ***
as.factor(School)9225  14.6678     1.0427  14.067  < 2e-16 ***
as.factor(School)9292  10.2800     1.4353   7.162 8.74e-13 ***
as.factor(School)9340  11.1797     1.1618   9.623  < 2e-16 ***
as.factor(School)9347  13.5393     0.8287  16.339  < 2e-16 ***
as.factor(School)9359  15.2717     0.8594  17.771  < 2e-16 ***
as.factor(School)9397  10.3560     0.9126  11.348  < 2e-16 ***
as.factor(School)9508  13.5746     1.0575  12.836  < 2e-16 ***
as.factor(School)9550  11.0903     1.1618   9.546  < 2e-16 ***
as.factor(School)9586  14.8637     0.8145  18.249  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.256 on 7025 degrees of freedom
Multiple R-squared:  0.8176,    Adjusted R-squared:  0.8135 
F-statistic: 196.8 on 160 and 7025 DF,  p-value: < 2.2e-16

Wir erhalten so geschätzte Mathematiknoten für jede einzelne Schule. Dabei

interessiert es uns vermutlich gar nicht so besonders, wie die einzelne geschätzte Mathematiknote einer spezifischen Schule ist (und deren Signifikanztest).
interessiert und viel eher die Frage, wie die einzelnen Schulen in ihren vorhergesagten Werten voneinander abweichen. Also wie groß die Varianz dieser Werte ist.

Ein einfaches Multilevelmodell

Wir könnten den Einfluss der Schulen als Random Effekt modellieren. Dafür brauchen wir zunächst zwei weitere Pakete, lme4 und lmerTest.

library(lme4)
library(lmerTest)

Wir möchten die Mathematiknote jedes einzelnen Schülers i in Gruppe j aufteilen in Anteile, die auf Unterschiede der jeweiligen Schulen j zurückgehen und Unterschiede die auch innerhalb der Schulen noch zwischen einzelnen Schülern i bestehen. (Erinnerung: Ähnliches haben wir bei der Quadratsummenzerlegung in der Varianzanalyse gemacht). Das Modell sieht also folgendermaßen aus:

\[ \begin{aligned} &\text{Level 1: }& MathAch_{ij} &= \beta_{0j} + r_{ij}, &&r_{ij} \sim N(0, \sigma^2) \\ &\text{Level 2: }& \beta_{0j} &= \gamma_{00} + u_{0j} &&u_{0j} \sim N(0, \tau_{00})\\ \hline &\text{Mixed: }& MathAch_{ij} &= \gamma_{00} + u_{0j} + r_{ij} \end{aligned} \]

Entsprechend ist in unserem Modell nur ein Fixed Effekt (\(\gamma_{00}\)) und zwei Komponenten, deren Varianz (\(\sigma^2\) und \(\tau_{00}\))im Modell enthalten ist. Diese gemischte (mixed) Gleichung wird nun entsprechend in R-Syntax übersetzt und das Modell geschätzt:

model2 <- lmer(formula = MathAch ~ 1 + (1|School), data = hsb)
summary(model2)

Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: MathAch ~ 1 + (1 | School)
   Data: hsb

REML criterion at convergence: 47116.7

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-3.06294 -0.75337  0.02658  0.76060  2.74221 

Random effects:
 Groups   Name        Variance Std.Dev.
 School   (Intercept)  8.614   2.935   
 Residual             39.148   6.257   
Number of obs: 7185, groups:  School, 160

Fixed effects:
            Estimate Std. Error       df t value Pr(>|t|)    
(Intercept)  12.6374     0.2444 156.6476   51.71   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Der Gesamtintercept \(\gamma_{00}\) wird also auf 12.63 geschätzt, die Varianz \(\tau_{00}\) der random Intercepts \(u_{0j}\) in den Schulen auf 8.61 und die Residualvarianz \(\sigma^2\) auf 39.15.

Um Abzuschätzen, wie viel Varianz also auf die Gruppenzugehörigkeit zurückgeht, können wir diese Werte ins Verhältnis setzen: \[ \begin{aligned} ICC &= \frac{\tau_{00}}{\tau_{00} + \sigma^2} \\ &= \frac{8.61}{8.61 + 39.15} \\ &= 0.18 \end{aligned} \]

Übung 1

Laden Sie den Datensatz “Pounds.csv” hier herunter, verschieben Sie ihn in Ihren Projektordner und lesen Sie ihn mit read.csv2() ein.

Lösung

pnd <- read.csv2("Pounds.csv")

Werfen Sie mit head() einen ersten Blick auf die Daten.

Lösung

head(pnd)

  group treat motivat pounds
1     1     0       4     15
2     1     0       4     17
3     1     0       4     15
4     1     0       4     17
5     1     0       4     16
6     1     0       6     18

Wie heißt die Variable, nach der die Personen gruppiert werden könnten?

Lösung

group

Wie heißt die Variable, die die Gewichtsabnahme der Personen enthält?

Lösung

pounds

Sie möchten herausfinden, welche Varianz die random Intercepts der Gruppen auf der Variable Pounds haben. Stellen Sie die Modellgleichungen für Level 1 & 2, sowie die gesamte (gemischte Gleichung) auf.

Lösung

\[ \begin{aligned} &\text{Level 1: }& pounds_{ij} &= \beta_{0j} + r_{ij} \\ &\text{Level 2: }& \beta_{0j} &= \gamma_{00} + u_{0j} \\ \hline &\text{Mixed: }& pounds_{ij} &= \gamma_{00} + u_{0j} + r_{ij} \end{aligned} \]

Schätzen Sie das Modell in R mit dem Befehl lmer() und weisen Sie das Ergebnis dem Objekt model.pounds zu.

Lösung

model.pounds <- lmer(formula = pounds ~ 1 + (1|group), data = pnd)

Zeigen Sie mit summary() das Ergebnis der Schätzung an und interpretieren Sie.

Lösung

summary(model.pounds)

Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: pounds ~ 1 + (1 | group)
   Data: pnd

REML criterion at convergence: 2220.2

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-4.1237 -0.5905 -0.0233  0.6181  2.8068 

Random effects:
 Groups   Name        Variance Std.Dev.
 group    (Intercept)  4.906   2.215   
 Residual             16.069   4.009   
Number of obs: 386, groups:  group, 40

Fixed effects:
            Estimate Std. Error     df t value Pr(>|t|)    
(Intercept)   15.115      0.409 36.650   36.95   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Berechnen Sie die ICC.

Lösung

\[ ICC = \frac{4.9}{4.9 + 16.1} = 0.23 \]

Teil 2

Hinzufügen eines Level-1 Prädiktors

Zurück zu unserem Beispiel in der Schule. Wir wollen natürlich herausfinden, woran es liegen könnte, dass die Schüler unterschiedliche Leistungen in Mathe haben.

Hypothese 1: Die Mathematikleistung hängt mit dem SES der Eltern zusammen.

Wir stellen zunächst die Level 1 & Level 2-Gleichungen auf:

\[ \begin{aligned} &\text{Level 1: }& MathAch_{ij} &= \beta_{0j} + \beta_{1j}SES_{ij} + r_{ij} && r_{ij} \sim N(0, \sigma^2) \\ &\text{Level 2: }& \beta_{0j} &= \gamma_{00} + u_{0j} && u_{0j} \sim N(0, \tau_{00}) \\ &\text{}& \beta_{1j} &= \gamma_{10} + u_{1j} && u_{1j} \sim N(0,\tau_{11})\\ \hline &\text{Mixed: }& MathAch_{ij} &= \gamma_{00} + \gamma_{10}SES_{ij} + u_{0j} + u_{1j}SES_{ij} + r_{ij} \end{aligned} \]

…und übersetzen das Ganze in lmer Syntax:

model3 <- lmer(formula = MathAch ~ 1 + SES + (1 + SES|School) , data = hsb)
summary(model3)

Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: MathAch ~ 1 + SES + (1 + SES | School)
   Data: hsb

REML criterion at convergence: 46640.3

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-3.12244 -0.73056  0.02165  0.75633  2.94314 

Random effects:
 Groups   Name        Variance Std.Dev. Corr 
 School   (Intercept)  4.8280  2.1973        
          SES          0.4129  0.6426   -0.11
 Residual             36.8295  6.0687        
Number of obs: 7185, groups:  School, 160

Fixed effects:
            Estimate Std. Error       df t value Pr(>|t|)    
(Intercept)  12.6703     0.1898 145.5062   66.74   <2e-16 ***
SES           2.3938     0.1181 157.5249   20.27   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
    (Intr)
SES -0.044

Der Effekt von SES, \(\gamma_{10} = 2.39\) ist signifikant (\(t(157.53) = 20.27\), \(p < 0.001\)), wir würden also entsprechend die \(H_0\), dass SES keinen Effekt auf die Mathematiknote hat, verwerfen. Entsprechend der Schätzung des Modells würden wir von einem mittleren Unterschied von 2.39 Punkten in der Mathematiknote ausgehen, wenn sich der SES zweier Schüler um 1 unterscheidet. Für Personen mit einem \(SES = 0\) wird eine Mathematiknote von 12.67 Punkten vorhergesagt.

Übung 2

Überprüfen Sie folgende Hypothese an Ihrem Übungsdatensatz:

Hypothese: Die Motivation der Personen hat einen Einfluss auf ihre Gewichtsabnahme.

Stellen Sie die Modellgleichungen auf.

Lösung

\[ \begin{aligned} &\text{Level 1: }& pounds_{ij} &= \beta_{0j} + \beta_{1j}motivat_{ij} + r_{ij} \\ &\text{Level 2: }& \beta_{0j} &= \gamma_{00} + u_{0j} \\ &\text{}& \beta_{1j} &= \gamma_{10} + u_{1j} \\ \hline &\text{Mixed:}& pounds_{ij} &= \gamma_{00} + \gamma_{10}motivat_{ij} + u_{0j} + u_{1j}motivat_{ij} + r_{ij} \end{aligned} \]

Schätzen Sie das Modell in R mit dem Befehl lmer() und weisen Sie das Ergebnis dem Objekt model.motivat zu.

Lösung

model.motivat <- lmer(formula = pounds ~ 1 + motivat + (1 + motivat|group), data = pnd)

Zeigen Sie das Ergebnis der Schätzung mit summary() an und interpretieren Sie.

Lösung

summary(model.motivat)

Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: pounds ~ 1 + motivat + (1 + motivat | group)
   Data: pnd

REML criterion at convergence: 1874.5

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-2.88513 -0.67353 -0.03211  0.64089  2.46892 

Random effects:
 Groups   Name        Variance Std.Dev. Corr 
 group    (Intercept) 9.4812   3.0791        
          motivat     0.9328   0.9658   -0.89
 Residual             5.9332   2.4358        
Number of obs: 386, groups:  group, 40

Fixed effects:
            Estimate Std. Error      df t value Pr(>|t|)    
(Intercept)   4.3695     0.7112 31.8174   6.144 7.34e-07 ***
motivat       3.1182     0.2107 37.0751  14.801  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
        (Intr)
motivat -0.925

Der Slope des Prädiktors motivat, \(\gamma_{10} = 3.12\) wird signifikant (\(t(37.07) = 14.8\), \(p < 0.001\)). Auf Basis der Stichprobe und einem Signifikanzniveau von \(\alpha = 0.05\) würden wir also entsprechend die Nullhypothese (Es gibt keinen Zusammenhang zwischen der Motivation und der Gewichtsabnahme) ablehnen. Entsprechend der Schätzung würden wir von einem mittleren Unterschied von 3.11 Pfund in der Gewichtsabnahme ausgehen, wenn sich zwei Personen um 1 in ihrer Motivation unterscheiden. Für Personen mit einer Ausprägung von \(motivat = 0\) wird eine Gewichtsabnahme von 4.36 Pfund vorhergesagt.

Grafiken

Befehle zum Erstellen anschaulicher Grafiken finden Sie im Paket sjPlot.

library(sjPlot)
plot_model(model = model3, type = "pred", terms = "SES")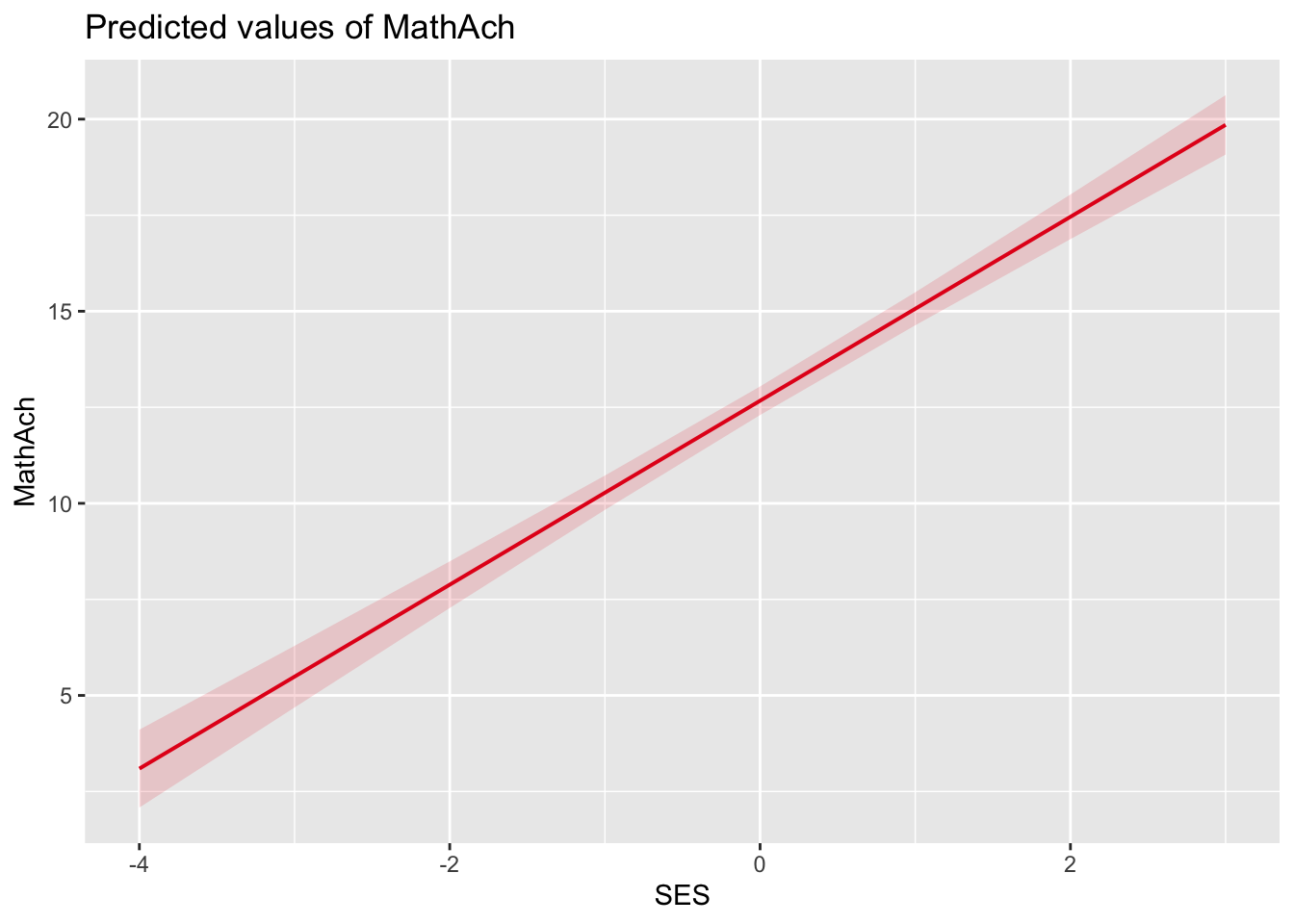

Übung 3

Erstellen Sie ein entsprechendes Plot für Ihren Übungsdatensatz und das eben in Übung 2 gerechnete Modell.

Lösung

plot_model(model = model.motivat, type = "pred", terms = "motivat")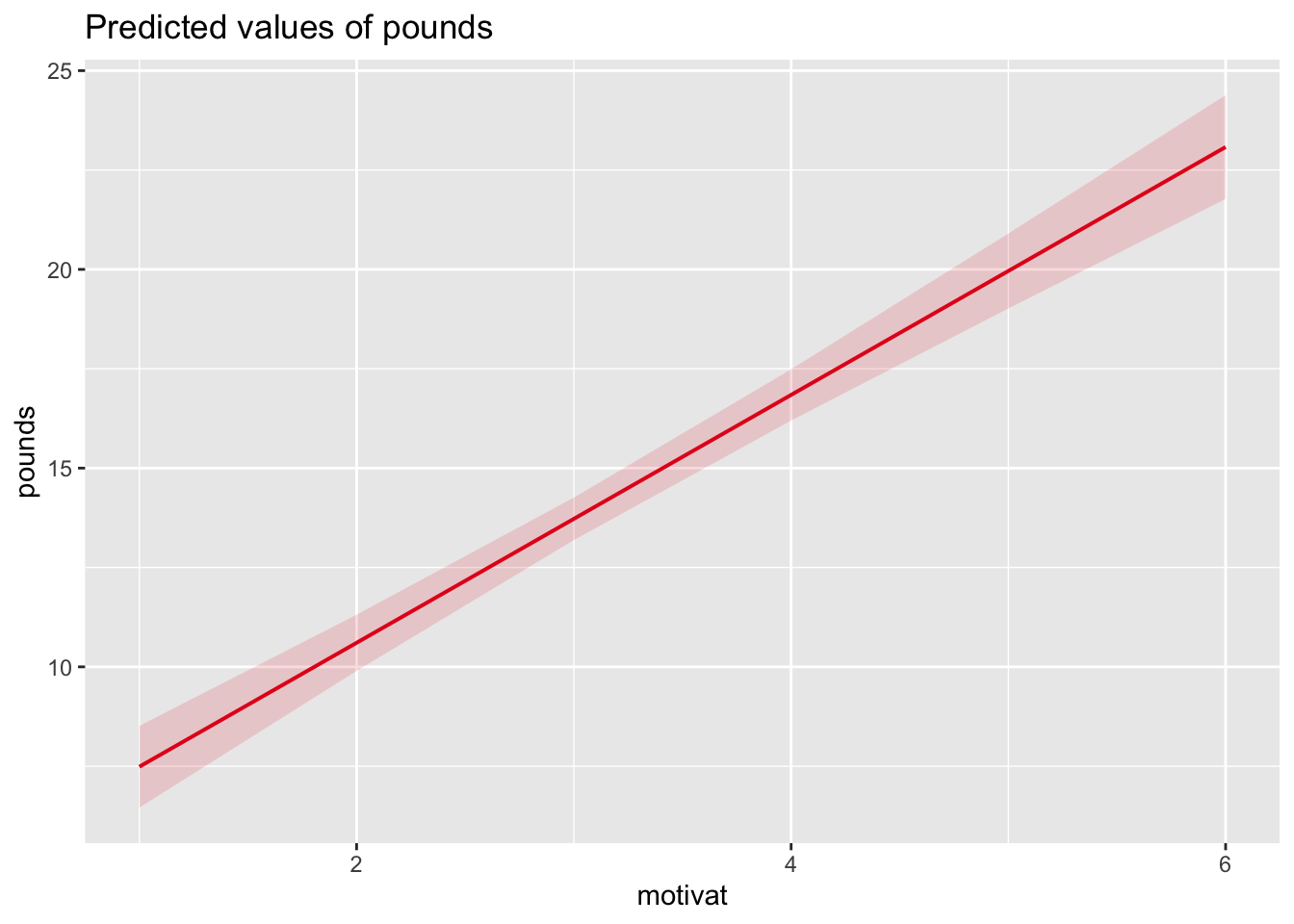

Welche Gewichtsabnahme wird für eine Person mit \(motivat = 5\) aus einer durchschnittlichen Gruppe vorhergesagt?

Lösung

Ca. 20 Pfund.

Wenn wir die Vorhersage (anstatt aus dem Plot abzulesen) mit R berechnen wollen, geht das mit der Funktion predict(). Dazu müssen wir das Modell übergeben, sowie einen data.frame mit den Prädiktorwerten einer neuen (hypothetischen) Beobachtung, für die eine Vorhersage berechnet werden soll. Das Argument re.form = NA bedeutet, dass bei der Vorhersage nur die fixed effects und keine random effects verwendet werden, d.h. \(u_{0j}\) und \(u_{1j}\) werden für die Vorhersage auf den Wert \(0\) gesetzt.

new_dat <- data.frame(motivat = 5)
predict(model.motivat, newdata = new_dat, re.form = NA)

       1 
19.96034

Teil 3

Hinzufügen eines Level 2 Prädiktors

Der nächste logische Schritt wäre zu schauen, ob wir die Varianzen der random Interceps und Slopes durch einen Level 2-Prädiktor wie den Schulsektor (Public = Öffentlich vs. Catholic = Privat) erklären können. Dies ist gleichbedeutend mit der Frage, ob der Sektor Unterschiede in der Mathematiknote und im Zusammenhang von Mathematiknote und SES erklären kann.

Hypothese 2a: Es gibt einen Zusammenhang zwischen dem Schulsektor und der Mathematiknote.

Hypothese 2b: Der Zusammenhang zwischen SES und Mathematiknote unterscheidet sich abhängig vom Schulsektor.

Dazu stellen wir zunächst die Modellgleichungen auf:

\[ \begin{aligned} &\text{Level 1: }& MathAch_{ij} &= \beta_{0j} + \beta_{1j}SES_{ij} + r_{ij} \qquad \qquad r_{ij} \sim N(0, \sigma^2)\\ &\text{Level 2: }& \beta_{0j} &= \gamma_{00} + \gamma_{01}Sector_j + u_{0j} \qquad \quad u_{0j} \sim N(0, \tau_{00})\\ &\text{}& \beta_{1j} &= \gamma_{10} + \gamma_{11}Sector_j + u_{1j} \qquad \quad u_{1j} \sim N(0, \tau_{11})\\ \hline &\text{Mixed: }& MathAch_{ij} &= \gamma_{00} + \gamma_{10}SES_{ij} + \gamma_{01}Sector_j + \gamma_{11}SES_{ij}Sector_j + u_{0j} + u_{1j}SES_{ij} + r_{ij} \end{aligned} \] …und schätzen das Modell in R:

model4 <- lmer(formula = MathAch ~ 1 + SES + Sector + SES:Sector + (1 + SES|School),
  data = hsb)
summary(model4)

Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: MathAch ~ 1 + SES + Sector + SES:Sector + (1 + SES | School)
   Data: hsb

REML criterion at convergence: 46569

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-3.07799 -0.72408  0.01548  0.75692  2.98471 

Random effects:
 Groups   Name        Variance Std.Dev. Corr
 School   (Intercept)  3.82300 1.9552       
          SES          0.07575 0.2752   1.00
 Residual             36.78699 6.0652       
Number of obs: 7185, groups:  School, 160

Fixed effects:
                  Estimate Std. Error        df t value Pr(>|t|)    
(Intercept)        13.8851     0.2568  139.8610  54.068  < 2e-16 ***
SES                 1.6442     0.1613 1431.6526  10.195  < 2e-16 ***
SectorPublic       -2.1269     0.3460  145.3172  -6.147 7.22e-09 ***
SES:SectorPublic    1.3133     0.2156 1399.7296   6.092 1.44e-09 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
            (Intr) SES    SctrPb
SES          0.104              
SectorPublc -0.742 -0.077       
SES:SctrPbl -0.078 -0.748  0.180
optimizer (nloptwrap) convergence code: 0 (OK)
boundary (singular) fit: see help('isSingular')

Hinweis: Die Ausprägung, die im Output hier den Namen der Variable geschrieben wird (“Public” hinter “Sector”) entspricht der Ausprägung 1. Der anderen Ausprägung von “Sector” (“Catholic”) wird automatisch die Ausprägung 0 zugewiesen.

Um die Interaktion beider Prädiktoren besser zu verstehen, setzen wir am besten für einen Prädiktor interpretierbare Werte ein. Nachdem Sector ohnehin nur die Ausprägungen 0 und 1 annehmen kann, nehmen wir den und lassen SES erstmal frei.

\[ \begin{aligned} \widehat{MathAch_{ij}} &= 13.9 + 1.6SES_{ij} + (-2.1)Sector_j + 1.3SES_{ij}Sector_j \\ \\ \widehat{MathAch_{ij}} &= \begin{cases} 13.9 + 1.6 SES_{ij} & \text{falls } Sector = 0,\\ (13.9 - 2.1) + (1.6 + 1.3) SES_{ij} & \text{falls } Sector = 1. \end{cases} \end{aligned} \]

Für private Schulen (\(Sector = 0\)) beträgt der Slope von SES \(\gamma_{10} = 1.6\). Da er signifikant wird (\(t(1430.11) = 10.2\), \(p < 0.001\)), würden wir für private Schulen die Nullhypothese “Es gibt keinen Zusammenhang zwischen SES und Mathematiknote” ablehnen.
Für öffentliche Schulen (\(Sector = 1\)) beträgt der Slope von SES nun \(\gamma_{10} + \gamma_{11} = (1.6 + 1.3)\) und ist damit um \(\gamma_{11} = 1.3\) verschieden vom Slope für private Schulen. Da dieser Unterschied signifikant wird (\(t(1398.2) = 6.1\), \(p < 0.001\)), würden wir die Nullhypothese, dass der Zusammenhang von SES und Mathematiknote zwischen den Sektoren nicht unterschiedlich ist, ablehnen. Offenbar ist dieser Zusammenhang für öffentliche Schulen stärker als für private.
Für private Schulen beträgt die erwartete Mathematiknote bei einem \(SES = 0\) im Mittel \(\gamma_{00} = 13.9\) Punkte.
Für öffentliche Schulen beträgt die erwartete Mathematiknote bei einem \(SES = 0\) um \(\gamma_{01} = 2.1\) Punkte weniger als bei öffentlichen. Da dieser Unterschied signifikant ist (\(t(145.3) = -6.1\), \(p < 0.001\)), verwerfen wir die Nullhypothese, dass die erwartete Mathematiknote bei Personen mit \(SES = 0\) für beide Schulsektoren gleich ist.

Zentrierung

An der Interpretation von iii. und iv. sehen wir, dass es leichter zu interpretieren wäre, wenn \(SES = 0\) eine inhaltliche Bedeutung hätte. Im vorliegenden Fall ist SES im Datensatz bereits grand-mean zentriert, wir können die Interpretation also auf “Personen mit durchschnittlichem SES” anwenden.

Für den Fall, dass noch keine Zentrierung vorliegt, müssten wir zunächst eine zentrierte Variable erstellen und das Modell damit schätzen. Für die Grand-mean Zentrierung müssen wir von den individuellen Werten der Personen den Gesamtmittelwert abziehen:

hsb$SES.c <- hsb$SES - mean(hsb$SES)

Im Anschluss könnten wir das gleiche Modell nun mit der Variable SES.c rechnen.

Übung 4

Überprüfen Sie analog zu oben im Übungsdatensatz folgende Hypothesen:

Hypothese 1: Es gibt einen Einfluss der Level 2-Variable Treatment auf den Zusammenhang zwischen Motivation und Gewichtsabnahme.

Hypothese 2: Für Personen mit durchschnittlicher Motivation ist die Gewichtsabnahme in einer Treatmentgruppe geringer als in einer Kontrollgruppe.

Gehen Sie dabei wie folgt vor:

Zentrieren Sie die Variable motivat am Gesamtmittelwert und erstellen Sie damit die neue Variable motivat.c

Lösung

pnd$motivat.c <- pnd$motivat - mean(pnd$motivat)

Nehmen Sie die zentrierte Variable in Ihr Modell auf und stellen Sie entsprechend die Modellgleichungen auf.

Lösung

\[ \begin{aligned} &\text{Level 1: }& pounds_{ij} &= \beta_{0j} + \beta_{1j}motivat.c_{ij} + r_{ij} \\ &\text{Level 2: }& \beta_{0j} &= \gamma_{00} + \gamma_{01}treat_j + u_{0j} \\ &\text{}& \beta_{1j} &= \gamma_{10} + \gamma_{11}treat_j + u_{1j} \\ \hline &\text{Mixed: }& pounds_{ij} &= \gamma_{00} + \gamma_{10}motivat.c_{ij} + \gamma_{01}treat_j + \gamma_{11}motivat.c_{ij}treat_j + u_{0j} + u_{1j}motivat.c_{ij} + r_{ij} \end{aligned} \]

Schätzen Sie das Modell in R und weisen Sie das Ergebnis dem Objekt model.treat zu.

Lösung

model.treat <- lmer(formula = pounds ~ 1 + motivat.c + treat + motivat.c:treat + 
    (1 + motivat.c|group), data = pnd)

Geben Sie die Zusammenfassung des Modells mit summary() an und interpretieren Sie. (Fixieren Sie dabei wie oben einen der Prädiktoren auf die Ausprägungen 0 und 1.)

Lösung

summary(model.treat)

Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: pounds ~ 1 + motivat.c + treat + motivat.c:treat + (1 + motivat.c |  
    group)
   Data: pnd

REML criterion at convergence: 1859.2

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-3.09320 -0.64310 -0.04462  0.65322  2.42244 

Random effects:
 Groups   Name        Variance Std.Dev. Corr
 group    (Intercept) 1.9670   1.4025       
          motivat.c   0.5563   0.7459   0.14
 Residual             5.9331   2.4358       
Number of obs: 386, groups:  group, 40

Fixed effects:
                Estimate Std. Error      df t value Pr(>|t|)    
(Intercept)      14.2554     0.4086 33.0767  34.891  < 2e-16 ***
motivat.c         2.3882     0.2917 34.0702   8.188 1.47e-09 ***
treat             1.5276     0.5287 33.3053   2.889  0.00674 ** 
motivat.c:treat   1.2450     0.3768 32.7581   3.304  0.00231 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
            (Intr) mtvt.c treat 
motivat.c    0.018              
treat       -0.773 -0.014       
motvt.c:trt -0.014 -0.774  0.053

\[ \begin{aligned} \widehat{pounds_{ij}} &= 14.26 + 2.39motivat.c_{ij} + 1.53treat_j + 1.25motivat.c_{ij}treat_j\\ \widehat{pounds_{ij}} &= \begin{cases} 14.26 + 2.39 motivat.c_{ij} & \text{falls } treat = 0 \\ (14.26 + 1.53) + (2.39 + 1.25) motivat.c_{ij} & \text{falls } treat = 1 \end{cases} \end{aligned} \]

Für Kontrollgruppen (\(treat = 0\)) beträgt der Zusammenhang zwischen Motivation und Gewichtsabnahme \(\gamma_{10} = 2.39\). Da signifikant (\(t(34.07) = 8.19\), \(p < 0.001\)) verwerfen wir die Nullhypothese und nehmen an, dass für diese Gruppen einen Zusammenhang zwischen Motivation und Gewichtsabnahme vorliegt. Unterscheiden sich zwei Teilnehmer einer Kontrollgruppe in ihrer Motivation um 1 beträgt der geschätzte Unterschied in ihrer Gewichtsabnahme 2.39 Pfund.
Für Treatmentgruppen (\(treat = 1\)) ist dieser Zusammenhang um \(\gamma_{11} = 1.25\) verschieden (größer). Da signifikant (\(t(32.76) = 3.30\), \(p = 0.007\)) verwerfen wir die Nullhypothese und nehmen an, dass für diese Gruppen der Zusammenhang unterschiedlich (und um 1.25 stärker) ist, als in den Kontrollgruppen.
Für Teilnehmer einer Kontrollgruppe ist bei durchschnittlicher Motivation (\(motivat.c = 0\)) die erwartete Gewichtsabnahme im Mittel bei \(\gamma_{00} = 14.26\) Pfund.
Für Teilnehmer einer Treatmentgruppe ist bei durchschnittlicher Motivation (\(motivat.c = 0\)) die erwartete Gewichtsabnahme im Mittel um \(\gamma_{10} = 1.53\) Pfund stärker als bei einer Kontrollgruppe. Da signifikant (\(t(33.31) = 2.89\), \(p = 0.002\)), verwerfen wir die Nullhypothese und nehmen an, dass bei durchschnittlicher Motivation Teilnehmer einer Treatmentgruppe stärker abnehmen als Teilnehmer einer Kontrollgruppe.

Grafiken

Wir können mit dem Paket sjPlot auch zwei Prädiktoren in ihrer Wirkung veranschaulichen:

plot_model(model = model4, type = "pred", terms = c("SES", "Sector"))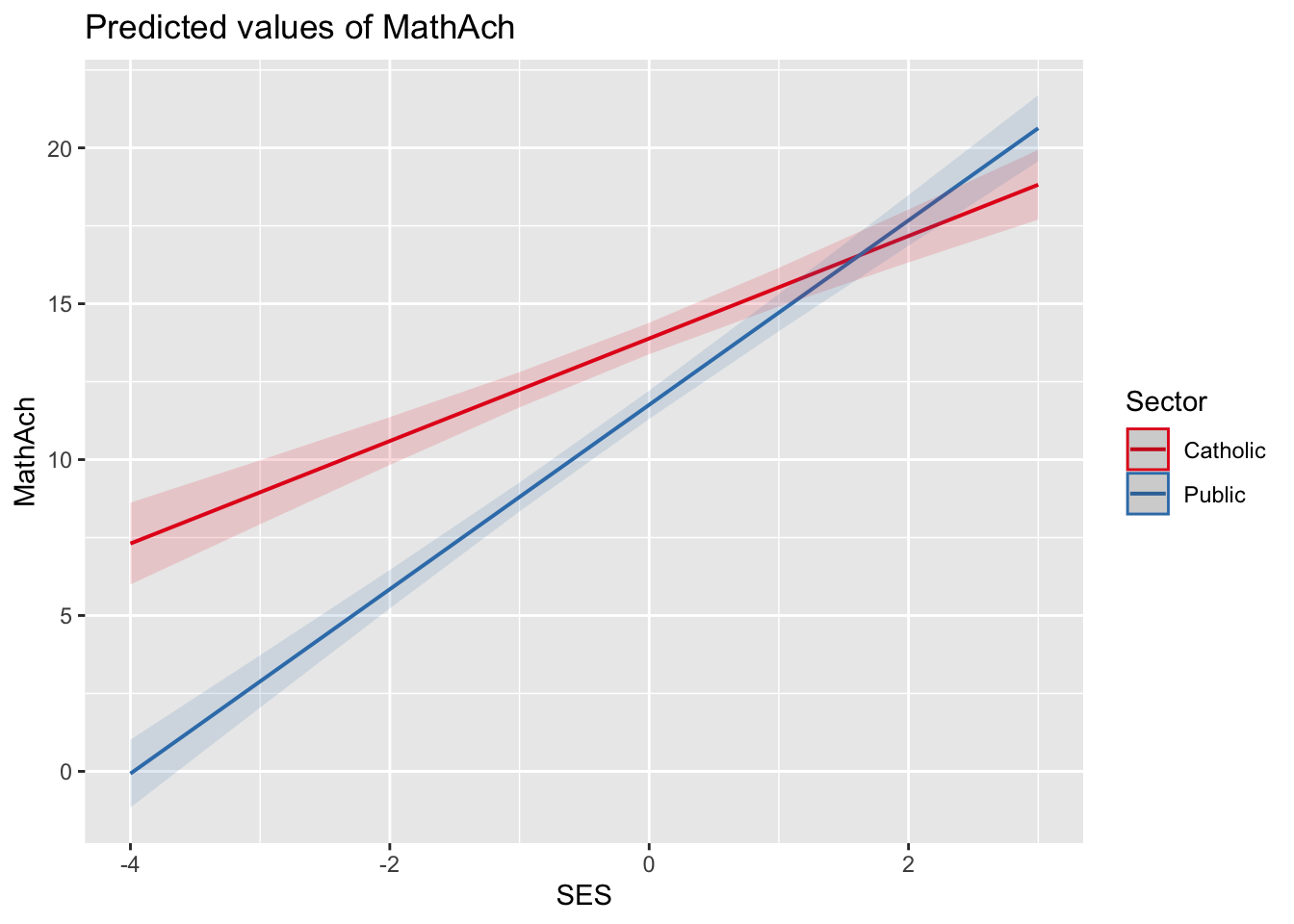

Übung 5

Veranschaulichen Sie die Zusammenhänge von Treatment und Motivation mit Gewichtsabnahme grafisch.

Lösung

plot_model(model = model.treat, type = 'pred', terms = c('motivat.c', 'treat'))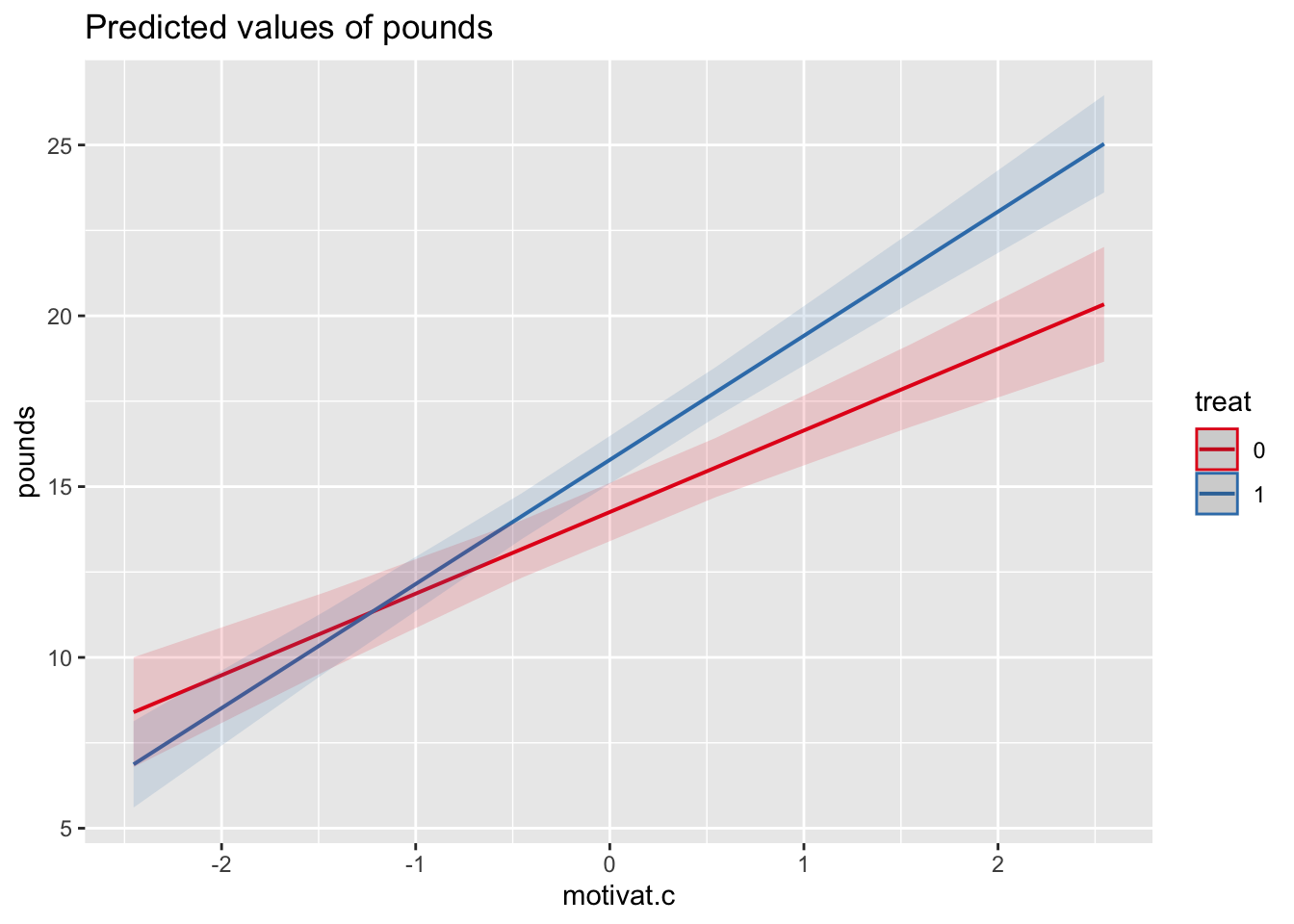

Ein weiteres Modell

Wollen wir die Schulgröße als Prädiktor in unser Modell mit aufnehmen, empfiehlt es sich, eine Zentrierung vorzunehmen. Die Schulgrößer ist in der absoluten Zahl der Schüler angegeben. Die Ausprägung 0 entspricht somit ohne Zentrierung einer Schule mit 0 Schülern. Ebenso könnte die Einheit für die Interpretation zu klein sein, da ein Unterschied um 1 bedeutet, dass sich zwei Schulen entsprechend in ihrer Größe nur um eine Person unterscheiden.

Ein Vorschlag wäre deshalb, die Zahl durch 100 zu teilen, um so 100er Schritte als Einheit zu erhalten und dann die resultierende Variable noch am Durchschnitt aller Schulen zu zentrieren. Als erstes erstellen wir die Variable Size.100:

hsb$Size.100 <- hsb$Size / 100

Als Zwischenrechnung müssen wir zunächst herausfinden, welche Anzahl pro Schule vorliegt, und dann darüber den Mittelwert bestimmen.

schulgroessen <- tapply(hsb$Size.100, hsb$School, unique)
mean(schulgroessen)

[1] 10.97825

Die durchschnittliche Schulgröße beträgt also 10.97 * 100 Personen. Diese Zahl können wir nun zur Zentrierung nutzen:

hsb$Size.100.c <- hsb$Size.100 - mean(schulgroessen)

model5 <- lmer(MathAch ~ SES*Size.100.c +  (1 + SES|School), hsb)
summary(model5)

Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: MathAch ~ SES * Size.100.c + (1 + SES | School)
   Data: hsb

REML criterion at convergence: 46643.7

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-3.09091 -0.72735  0.02391  0.76005  2.96579 

Random effects:
 Groups   Name        Variance Std.Dev. Corr 
 School   (Intercept)  4.8731  2.2075        
          SES          0.3444  0.5869   -0.08
 Residual             36.8179  6.0678        
Number of obs: 7185, groups:  School, 160

Fixed effects:
                Estimate Std. Error        df t value Pr(>|t|)    
(Intercept)     12.67931    0.19053 145.05336  66.547  < 2e-16 ***
SES              2.39044    0.11619 157.01972  20.573  < 2e-16 ***
Size.100.c      -0.02656    0.03065 149.99295  -0.867  0.38758    
SES:Size.100.c   0.04931    0.01867 161.22127   2.641  0.00907 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
            (Intr) SES    S.100.
SES         -0.031              
Size.100.c   0.012  0.027       
SES:Sz.100.  0.028  0.006  0.037

plot_model(model5, type = "pred", terms = c("SES", "Size.100.c"), colors = "Blues")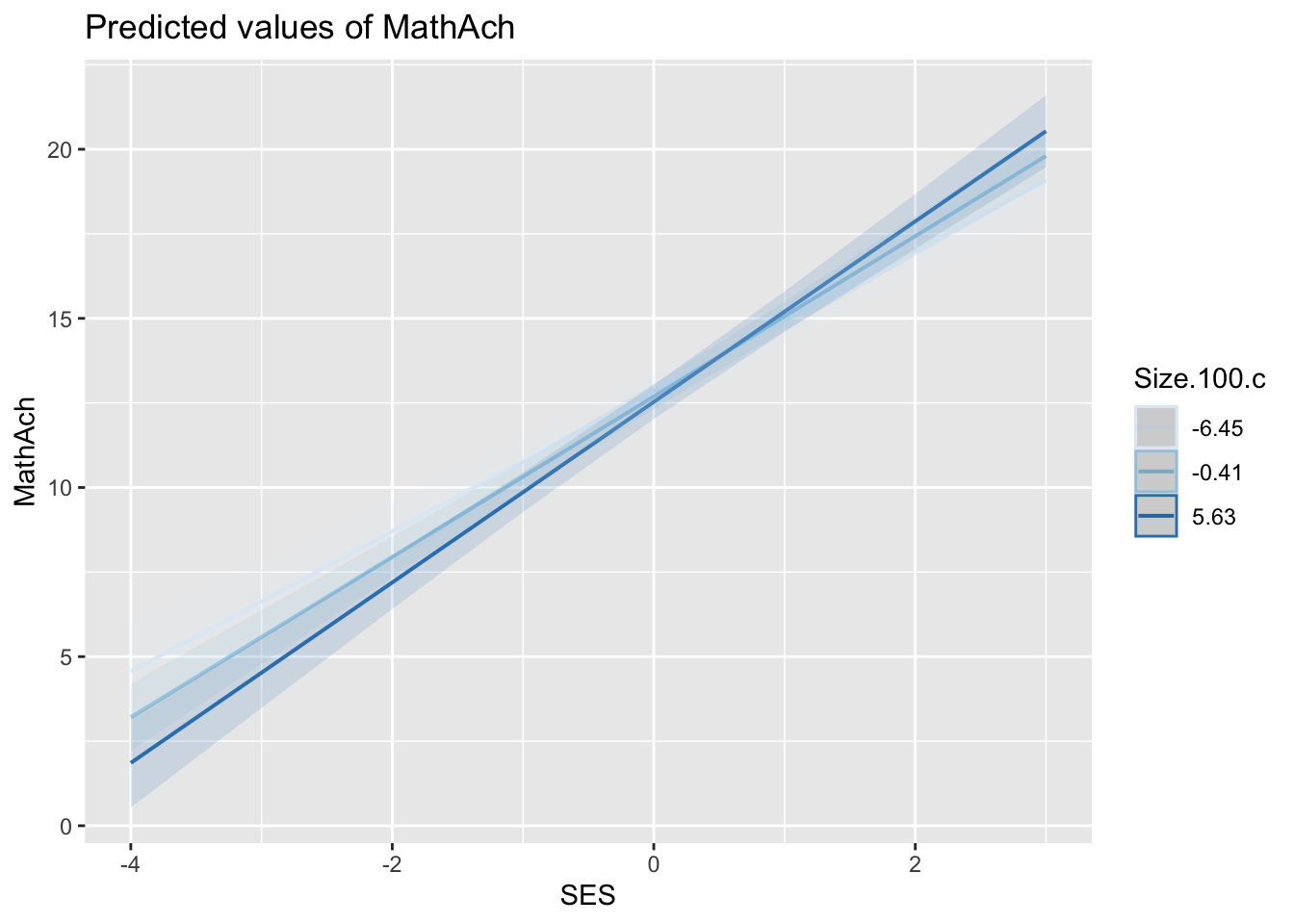

Durch die Grafik und die Ergebnisse oben lässt sich unschwer erkennen, dass der Einfluss des SES auf die Mathematiknote mit steigender Schulgröße größer wird. Bei einem Veränderung der Schulgröße um 1 (was hundert Schülern entspricht) wird eine Veränderung des Zusammenhangs von SES mit der Mathematiknote um 0.049 vorhergesagt. Diese Interaktion ist signifikant (\(t(161.23) = 2.64\), \(p = 0.009\)), weshalb wir die entsprechende Nullhypothese verwerfen und annehmen, dass bei Schulen mit einer um hundert Schülern größeren Schulgröße der SES einen stärkeren Zusammenhang mit der Mathematiknote aufweist, als bei kleineren Schulen.