neo_dat <- read.csv(file = "data/NEO_original.csv")R-Nachschlagewerk in Statistik 1 und 2
1 Vorbereitungen
Daten
Im Folgenden zeigen wir nützliche R-Befehle für das Modul Statistik 1 sowie das Modul Statistik 2 am Beispiel eines Datensatzes zum NEO FFI. Dazu lesen wir diesen erstmal ein.
Und so sieht der Datensatz (die ersten zwanzig Zeilen davon) aus:
| Sex | GermanAsNativeLanguage | HighestEducation | Age | N1 | E1 | O1 | A1 | C1 | N2 | E2 | O2 | A2 | C2 | N3 | E3 | O3 | A3 | C3 | N4 | E4 | O4 | A4 | C4 | N5 | E5 | O5 | A5 | C5 | N6 | E6 | O6 | A6 | C6 | N7 | E7 | O7 | A7 | C7 | N8 | E8 | O8 | A8 | C8 | N9 | E9 | O9 | A9 | C9 | N10 | E10 | O10 | A10 | C10 | N11 | E11 | O11 | A11 | C11 | N12 | E12 | O12 | A12 | C12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| female | yes | mittlere_Reife | 28 | 1 | 3 | 3 | 2 | 3 | 3 | 2 | 3 | 1 | 3 | 4 | 1 | 2 | 3 | 1 | 3 | 3 | 2 | 1 | 2 | 3 | 3 | 0 | 2 | 3 | 2 | 0 | 3 | 1 | 3 | 3 | 2 | 4 | 0 | 1 | 4 | 2 | 2 | 1 | 1 | 3 | 1 | 3 | 2 | 0 | 2 | 4 | 3 | 4 | 2 | 2 | 3 | 3 | 0 | 2 | 4 | 0 | 3 | 3 | 2 |
| female | yes | Fachabitur_Abitur | 45 | 0 | 0 | 3 | 4 | 3 | 1 | 2 | 4 | 4 | 3 | 1 | 2 | 3 | 3 | 3 | 0 | 2 | 0 | 3 | 4 | 1 | 0 | 3 | 3 | 3 | 2 | 0 | 2 | 2 | 3 | 0 | 0 | 3 | 3 | 3 | 0 | 2 | 2 | 3 | 4 | 1 | 3 | 3 | 1 | 3 | 1 | 0 | 4 | 4 | 3 | 1 | 0 | 4 | 3 | 3 | 1 | 1 | 3 | 4 | 3 |
| female | yes | Hauptschulabschluss | 57 | 2 | 4 | 0 | 4 | 4 | 2 | 3 | 2 | 3 | 3 | 3 | 4 | 3 | 4 | 2 | 3 | 4 | 2 | 3 | 3 | 3 | 3 | 3 | 2 | 3 | 1 | 1 | 3 | 1 | 4 | 3 | 1 | 3 | 3 | 2 | 3 | 2 | 1 | 4 | 4 | 3 | 1 | 1 | 1 | 4 | 1 | 2 | 2 | 3 | 3 | 3 | 2 | 2 | 1 | 3 | 3 | 1 | 2 | 3 | 1 |
| male | yes | Fachabitur_Abitur | 26 | 1 | 2 | 3 | 3 | 3 | 1 | 2 | 3 | 3 | 3 | 2 | 2 | 3 | 3 | 3 | 2 | 2 | 3 | 3 | 3 | 1 | 1 | 2 | 2 | 3 | 3 | 2 | 2 | 3 | 1 | 1 | 1 | 3 | 3 | 3 | 2 | 2 | 4 | 2 | 3 | 1 | 1 | 2 | 1 | 3 | 3 | 2 | 3 | 3 | 2 | 1 | 2 | 3 | 2 | 3 | 3 | 1 | 3 | 1 | 3 |
| female | yes | Fachabitur_Abitur | 27 | 3 | 3 | 2 | 3 | 2 | 3 | 1 | 3 | 1 | 1 | 4 | 2 | 3 | 4 | 3 | 3 | 4 | 4 | 0 | 3 | 4 | 2 | 4 | 1 | 4 | 0 | 0 | 4 | 0 | 0 | 3 | 3 | 4 | 2 | 4 | 4 | 2 | 4 | 2 | 4 | 2 | 0 | 4 | 1 | 1 | 4 | 3 | 4 | 2 | 3 | 2 | 2 | 4 | 1 | 1 | 3 | 0 | 4 | 3 | 4 |
| female | yes | qualifizierter_Hauptschulabschluss | 46 | 3 | 0 | 1 | 3 | 3 | 3 | 3 | 1 | 2 | 1 | 3 | 2 | 2 | 3 | 3 | 3 | 2 | 3 | 3 | 3 | 3 | 3 | 1 | 2 | 2 | 3 | 1 | 3 | 1 | 1 | 2 | 1 | 3 | 4 | 2 | 3 | 2 | 2 | 3 | 4 | 3 | 1 | 3 | 1 | 3 | 3 | 2 | 1 | 4 | 4 | 3 | 2 | 4 | 2 | 1 | 4 | 3 | 2 | 1 | 3 |
| female | yes | Hochschulabschluss | 38 | 2 | 2 | 2 | 3 | 4 | 1 | 3 | 2 | 4 | 3 | 1 | 4 | 1 | 4 | 4 | 1 | 2 | 2 | 3 | 4 | 1 | 1 | 1 | 2 | 3 | 0 | 2 | 3 | 3 | 3 | 1 | 2 | 3 | 3 | 3 | 2 | 3 | 2 | 3 | 4 | 1 | 3 | 1 | 2 | 3 | 1 | 3 | 2 | 3 | 3 | 1 | 3 | 2 | 2 | 3 | 2 | 2 | 2 | 3 | 2 |
| female | yes | Fachabitur_Abitur | 21 | 1 | 3 | 1 | 3 | 4 | 2 | 3 | 3 | 2 | 3 | 1 | 1 | 3 | 3 | 4 | 2 | 3 | 3 | 3 | 3 | 1 | 3 | 3 | 1 | 4 | 1 | 3 | 3 | 3 | 2 | 1 | 1 | 3 | 2 | 3 | 1 | 3 | 3 | 3 | 3 | 1 | 2 | 3 | 1 | 3 | 2 | 3 | 3 | 2 | 3 | 1 | 3 | 3 | 1 | 3 | 1 | 2 | 3 | 1 | 2 |
| female | yes | abgeschlossene_Berufsausbildung | 30 | 3 | 3 | 2 | 2 | 4 | 1 | 3 | 2 | 3 | 3 | 1 | 3 | 3 | 1 | 3 | 1 | 2 | 1 | 3 | 4 | 1 | 3 | 3 | 1 | 3 | 0 | 1 | 3 | 2 | 3 | 1 | 2 | 3 | 3 | 3 | 1 | 3 | 3 | 1 | 4 | 1 | 3 | 3 | 2 | 4 | 1 | 3 | 3 | 2 | 3 | 1 | 3 | 3 | 1 | 3 | 3 | 2 | 1 | 3 | 2 |
| female | yes | Hochschulabschluss | 33 | 2 | 2 | 3 | 3 | 2 | 1 | 3 | 1 | 4 | 3 | 1 | 2 | 2 | 3 | 4 | 1 | 3 | 3 | 4 | 3 | 1 | 1 | 2 | 2 | 2 | 1 | 3 | 1 | 3 | 3 | 1 | 1 | 3 | 2 | 2 | 1 | 2 | 3 | 3 | 3 | 1 | 3 | 1 | 3 | 1 | 1 | 1 | 1 | 3 | 2 | 1 | 2 | 2 | 1 | 4 | 3 | 2 | 1 | 2 | 2 |
| male | yes | Hochschulabschluss | 38 | 1 | 2 | 3 | 3 | 3 | 3 | 1 | 2 | 3 | 3 | 3 | 2 | 2 | 3 | 2 | 2 | 3 | 3 | 3 | 3 | 1 | 2 | 3 | 3 | 2 | 3 | 4 | 3 | 3 | 1 | 1 | 1 | 3 | 3 | 3 | 2 | 2 | 4 | 3 | 3 | 1 | 3 | 1 | 2 | 3 | 3 | 1 | 3 | 3 | 3 | 1 | 2 | 3 | 3 | 3 | 1 | 3 | 1 | 1 | 2 |
| male | yes | Fachabitur_Abitur | 34 | 0 | 3 | 1 | 4 | 3 | 2 | 3 | 4 | 4 | 4 | 3 | 3 | 3 | 4 | 4 | 2 | 3 | 3 | 3 | 4 | 0 | 1 | 3 | 3 | 3 | 1 | 3 | 3 | 1 | 4 | 1 | 3 | 4 | 4 | 4 | 1 | 3 | 4 | 4 | 4 | 0 | 0 | 3 | 3 | 4 | 1 | 1 | 3 | 4 | 4 | 0 | 2 | 3 | 3 | 4 | 0 | 4 | 4 | 2 | 3 |
| female | yes | Hochschulabschluss | 29 | 3 | 1 | 2 | 3 | 3 | 1 | 3 | 1 | 3 | 3 | 3 | 3 | 3 | 2 | 3 | 2 | 2 | 1 | 3 | 3 | 2 | 1 | 1 | 1 | 3 | 2 | 1 | 1 | 2 | 2 | 3 | 2 | 3 | 3 | 3 | 3 | 3 | 2 | 2 | 3 | 2 | 3 | 3 | 1 | 1 | 2 | 1 | 1 | 3 | 3 | 2 | 2 | 3 | 2 | 3 | 1 | 1 | 3 | 3 | 3 |
| female | yes | Hochschulabschluss | 34 | 3 | 1 | 2 | 3 | 2 | 3 | 3 | 2 | 3 | 3 | 3 | 3 | 3 | 1 | 1 | 3 | 1 | 3 | 3 | 3 | 3 | 1 | 1 | 1 | 3 | 3 | 1 | 2 | 1 | 1 | 1 | 1 | 1 | 2 | 3 | 3 | 3 | 3 | 1 | 3 | 3 | 3 | 3 | 1 | 3 | 3 | 1 | 1 | 3 | 3 | 3 | 2 | 2 | 1 | 1 | 3 | 1 | 3 | 3 | 1 |
| male | yes | Hochschulabschluss | 24 | 1 | 2 | 3 | 2 | 0 | 1 | 3 | 4 | 3 | 2 | 1 | 2 | 3 | 4 | 4 | 1 | 3 | 4 | 3 | 3 | 1 | 2 | 4 | 1 | 2 | 0 | 2 | 3 | 1 | 1 | 3 | 1 | 3 | 3 | 2 | 1 | 2 | 4 | 3 | 3 | 0 | 2 | 3 | 1 | 2 | 1 | 2 | 4 | 1 | 2 | 0 | 3 | 4 | 1 | 2 | 2 | 3 | 4 | 1 | 2 |
| female | yes | Hochschulabschluss | 31 | 1 | 4 | 3 | 4 | 2 | 1 | 4 | 3 | 4 | 3 | 3 | 3 | 3 | 4 | 1 | 2 | 4 | 3 | 4 | 4 | 2 | 4 | 3 | 3 | 2 | 0 | 4 | 3 | 3 | 1 | 3 | 2 | 4 | 4 | 2 | 1 | 4 | 2 | 4 | 4 | 1 | 3 | 2 | 4 | 3 | 2 | 2 | 4 | 4 | 3 | 1 | 3 | 3 | 1 | 1 | 2 | 4 | 3 | 4 | 3 |
| male | yes | Fachabitur_Abitur | 26 | 2 | 1 | 0 | 3 | 3 | 3 | 2 | 3 | 3 | 2 | 3 | 2 | 3 | 3 | 1 | 2 | 2 | 1 | 3 | 4 | 3 | 1 | 2 | 1 | 3 | 4 | 2 | 1 | 1 | 1 | 3 | 1 | 2 | 3 | 3 | 3 | 2 | 2 | 1 | 3 | 1 | 3 | 3 | 2 | 1 | 2 | 1 | 3 | 3 | 3 | 2 | 2 | 4 | 3 | 3 | 2 | 1 | 3 | 1 | 4 |
| female | yes | Fachabitur_Abitur | 24 | 3 | 1 | 1 | 4 | 4 | 2 | 3 | 4 | 4 | 4 | 1 | 3 | 3 | 3 | 4 | 2 | 3 | 3 | 2 | 4 | 3 | 0 | 1 | 3 | 4 | 1 | 1 | 1 | 3 | 4 | 1 | 3 | 4 | 3 | 4 | 3 | 3 | 4 | 3 | 4 | 1 | 2 | 3 | 3 | 4 | 1 | 2 | 3 | 4 | 4 | 1 | 4 | 4 | 3 | 4 | 4 | 2 | 4 | 2 | 4 |
| male | yes | Hochschulabschluss | 23 | 2 | 1 | 3 | 4 | 3 | 1 | 4 | 4 | 4 | 4 | 1 | 2 | 4 | 1 | 3 | 4 | 1 | 3 | 1 | 3 | 3 | 1 | 2 | 3 | 4 | 3 | 0 | 1 | 3 | 2 | 0 | 3 | 1 | 4 | 4 | 1 | 3 | 0 | 1 | 4 | 1 | 2 | 4 | 1 | 3 | 2 | 1 | 4 | 3 | 4 | 2 | 2 | 3 | 2 | 4 | 4 | 1 | 4 | 1 | 4 |
| male | yes | abgeschlossene_Berufsausbildung | 29 | 3 | 1 | 3 | 3 | 3 | 2 | 0 | 4 | 2 | 2 | 3 | 0 | 2 | 2 | 1 | 3 | 2 | 3 | 2 | 3 | 3 | 2 | 3 | 1 | 2 | 3 | 0 | 3 | 2 | 1 | 2 | 0 | 3 | 2 | 2 | 3 | 1 | 4 | 3 | 2 | 4 | 0 | 2 | 2 | 1 | 3 | 3 | 4 | 3 | 3 | 3 | 1 | 3 | 2 | 2 | 2 | 1 | 2 | 4 | 3 |
Pakete
Manche der gezeigten Funktionen kommen aus Paketen, die zunächst geladen werden müssen.1 Die Pakete dplyr (Wickham u. a. 2023), psych (William Revelle 2024) und ggplot2 (Wickham 2016) laden wir gleich zu Beginn, damit wir deren Befehle gleich nutzen können.
library(dplyr)
library(psych)
library(ggplot2)2 Statistik 1
Im Modul Statistik 1 werden Deskriptive Statistiken und erste Methoden der Inferenzstatistik gelehrt, sowie deren Wahrscheinlichkeitstheoretische Grundlagen.
2.1 Deskriptive Statistiken und Grafiken
Häufigkeiten (absolut, relativ, kumuliert) bei diskreten Daten
Zunächst erstellen wir mit table() einfache absolute Häufigkeiten, hier zum Beispiel für die Variable HighestEducation (höchster Bildungsabschluss) des Datensatzes. Das Ergebnis weisen wir dem Objekt H zu.
H <- table(neo_dat$HighestEducation)Mit der Funktion prop.table() können wir daraus nun relative Häufigkeiten machen:
h <- prop.table(H)
h <- round(h, digits = 2) # das Ergebnis runden wir noch auf 2 Kommastellen.Mit cumsum() können wir aus H und h jeweils kumulierte absolute/relative Häufigkeiten erstellen.
Hkum <- cumsum(H)
hkum <- cumsum(h)
hkum <- round(hkum, digits = 2) # das Ergebnis runden wir noch auf 2 KommastellenAlle vier Informationen können wir noch mit cbind() in einer Matrix zusammenfassen.
cbind(H, h, Hkum, hkum) H h Hkum hkum
abgeschlossene_Berufsausbildung 87 0.15 87 0.15
Fachabitur_Abitur 210 0.37 297 0.52
Hauptschulabschluss 9 0.02 306 0.54
Hochschulabschluss 162 0.29 468 0.83
kein_Schulabschluss 3 0.01 471 0.84
mittlere_Reife 81 0.14 552 0.98
qualifizierter_Hauptschulabschluss 14 0.02 566 1.00Häufigkeiten bei stetigen Daten
Sobald die interessierenden Daten stetig sind, müssen wir beim Beschreiben der Daten mittels Häufigkeiten definieren, in welche Kategorien die einzelnen Ausprägungen zusammengefasst werden soll. Als Beispielvariable nehmen wir dazu die Variable Age, die das Alter der ProbandInnen in Lebensjahren enthält. Die Personen in unserer Stichprobe haben auf dieser Variable insgesamt 52 verschiedene Angaben gemacht.
Um zu entscheiden, in welche Kategorien die Angaben zusammengefasst werden sollen, sehen wir uns zunächst die Spannbreite der gegebenen Antworten an:
range(neo_dat$Age)[1] 16 71Wir stellen fest, dass das Minimum 16 und das Maximum 71 Jahre beträgt. Eine Möglichkeit wäre, die Ausprägungen in 7 Abschnitte von jeweils 10 Jahren Breite einzusortieren. Hierbei steht die [ für eine ins Intervall eingeschlossene Grenze und die ) für eine Grenze die aus dem Intervall ausgeschlossen wird.
\([10; 20), [20; 30), [30, 40), [40; 50), [50; 60), [60; 70), [70; 80)\)
Diese Einteilung können wir mit dem Befehl cut() erreichen. Als erstes Argument müssen wir hier angeben, welche Variable wir in Kategorien sortieren wollen. Im zweiten Argument breaks geben wir einen Vektor mit den gewünschten Kategoriengrenzen an. Mit dem dritten Argument right = FALSE geben wir an, dass die jeweils rechte Kategoriengrenze nicht im Intervall enthalten sein soll. Das Ergebnis der Einteilung weisen wir einer neuen Spalte Age_cat in unserem Datensatz zu.
neo_dat$Age_cat <- cut(neo_dat$Age,
breaks = c(10, 20, 30, 40, 50, 60, 70, 80),
right = FALSE)Wir können nun - für eine kurze Überprüfung ob alles so funktioniert hat wie gewünscht - mal die Ausprägungen der unveränderten Variable Age neben die neue Variable Age_cat mit den Alterkategorien stellen (zur übersichtlicheren Darstellung nur die Zeilen 1 - 20):
neo_dat[1:20, c('Age', 'Age_cat')] Age Age_cat
1 28 [20,30)
2 45 [40,50)
3 57 [50,60)
4 26 [20,30)
5 27 [20,30)
6 46 [40,50)
7 38 [30,40)
8 21 [20,30)
9 30 [30,40)
10 33 [30,40)
11 38 [30,40)
12 34 [30,40)
13 29 [20,30)
14 34 [30,40)
15 24 [20,30)
16 31 [30,40)
17 26 [20,30)
18 24 [20,30)
19 23 [20,30)
20 29 [20,30)Wenn wir mit unserer Zuordnung zufrieden sind, können wir nun mit der neu gebildeten Variable der Alterskategorien die gleichen Methoden anwenden, um eine Häufigkeitsverteilung der Merkmalsausprägungen zu erhalten.
cbind(H = table(neo_dat$Age_cat),
h = round(prop.table(table(neo_dat$Age_cat)), 2),
Hkum = cumsum(table(neo_dat$Age_cat)),
hkum = cumsum(round(prop.table(table(neo_dat$Age_cat)), 2))) H h Hkum hkum
[10,20) 34 0.06 34 0.06
[20,30) 296 0.52 330 0.58
[30,40) 127 0.22 457 0.80
[40,50) 66 0.12 523 0.92
[50,60) 27 0.05 550 0.97
[60,70) 14 0.02 564 0.99
[70,80) 2 0.00 566 0.99Balkendiagramme und Histogramme
Diskrete Daten
Die Häufigkeiten die wir in Abschnitt 2.1.1 erstellt haben, können wir nun mit Balkendiagrammen veranschaulichen 2.
barplot(H, main = 'Absolute Häufigkeiten')
barplot(h, main = 'Relative Häufigkeiten')
barplot(Hkum, main = 'Absolute kumulierte Häufigkeiten')
barplot(hkum, main = 'Relative kumulierte Häufigkeiten')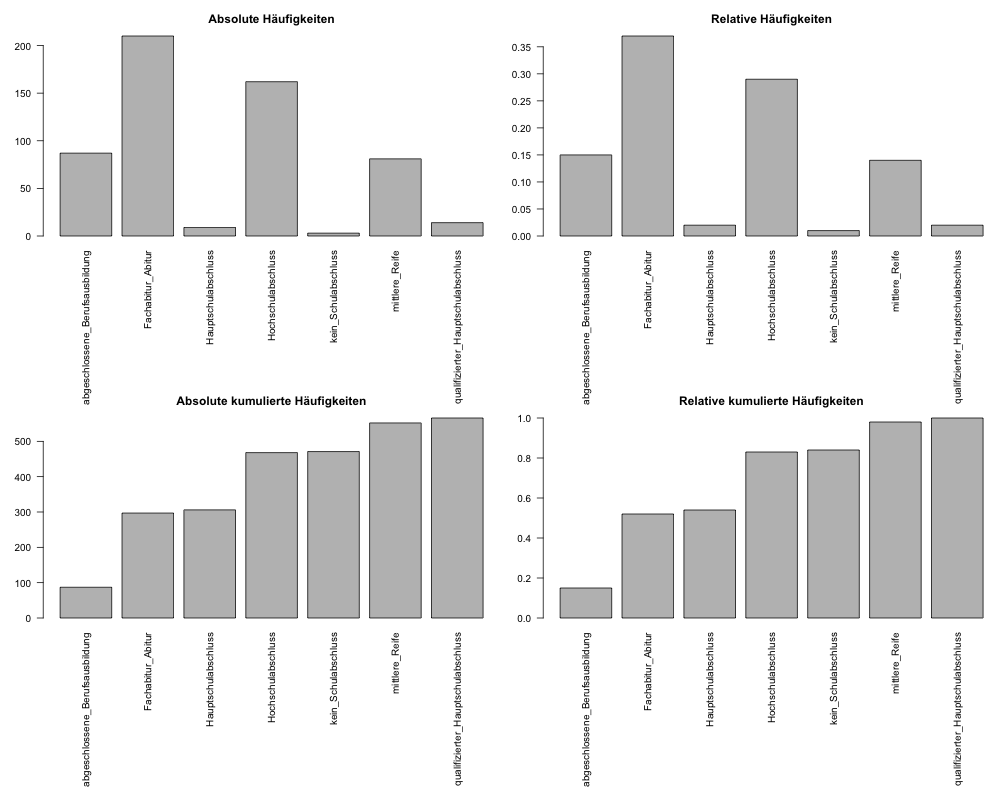
Die gleiche Darstellung können wir auch für die oben gebildete Variable der Alterskategorien erstellen 3:
barplot(table(neo_dat$Age_cat))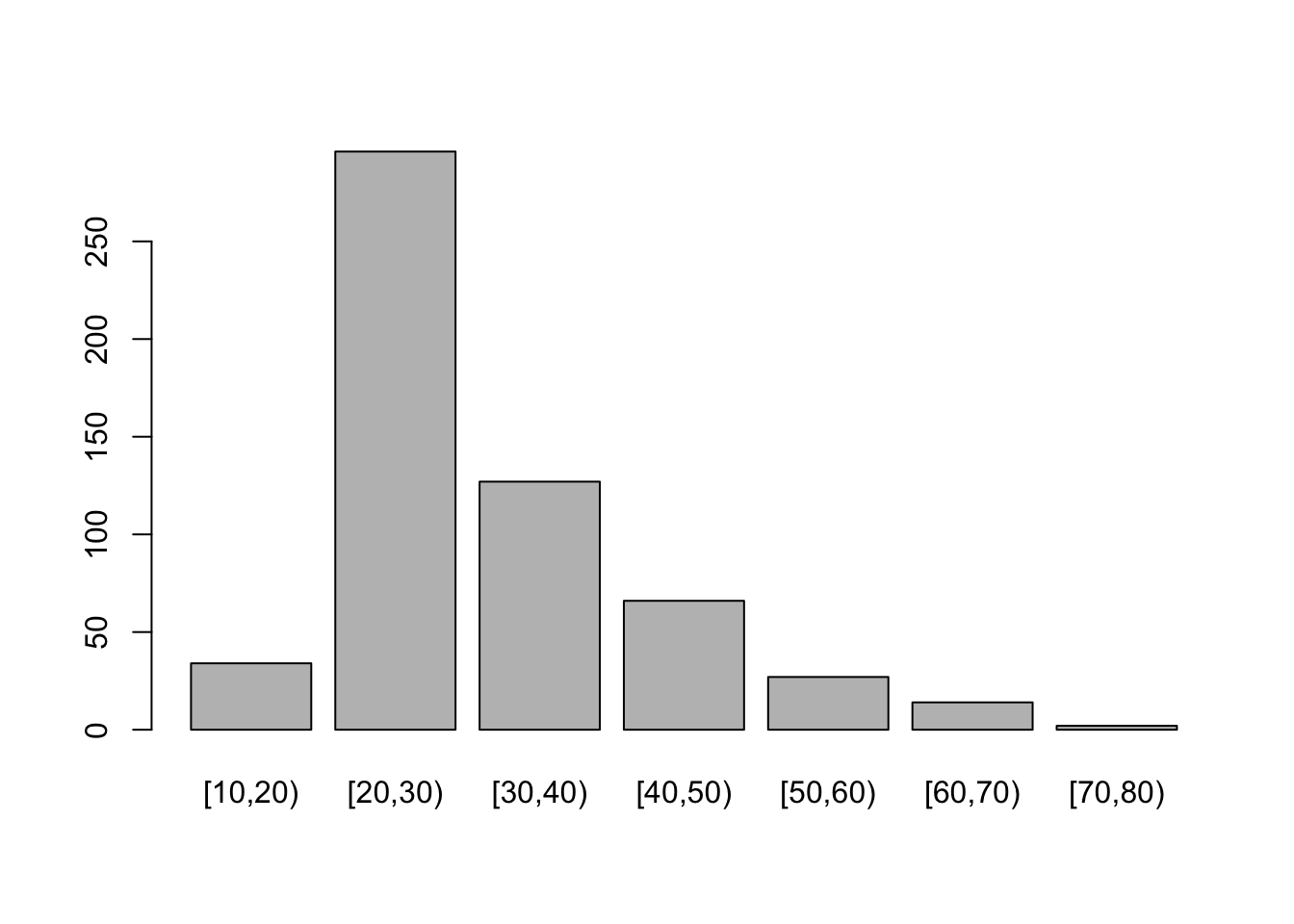
Stetige Daten
Bei stetigen Daten können wir auch gleich ein Histogramm der ursprünglichen Variable Age erstellen. Der Algorithmus kann dabei automatisch versuchen, die Daten in sinnvolle Kategorien einzuteilen. Es ist aber auch möglich, so wie oben die Kategoriengrenzen vorzugeben. Wenn wir stetige Daten also nur grafisch veranschaulichen wollen, reicht es, ein Histogramm zu erstellen ohne die Einteilung in Kategorien vorher explizit vorzunehmen.
hist(neo_dat$Age, breaks = c(10, 20, 30, 40, 50, 60, 70, 80))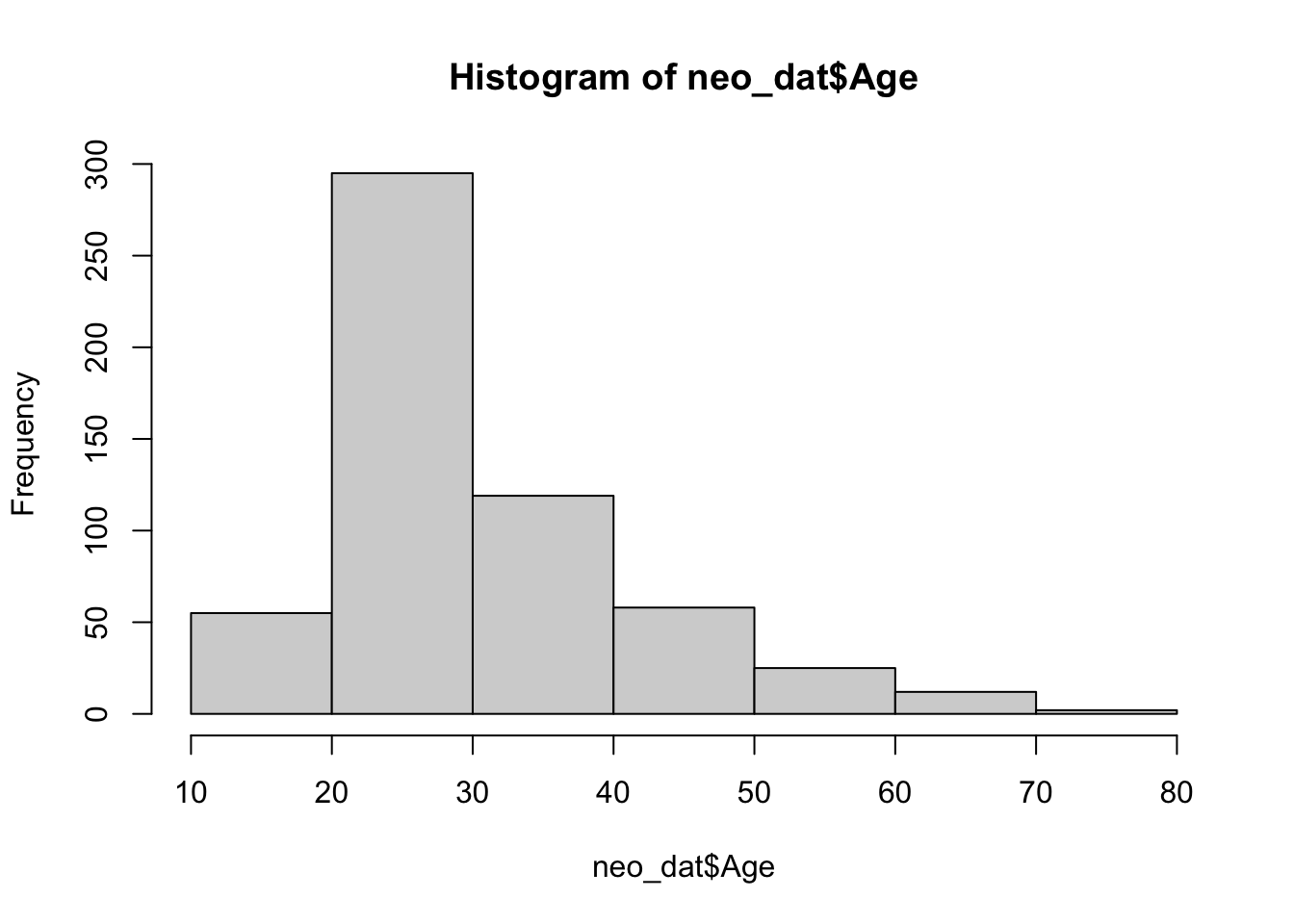
Lagemaße
Modus
Für die Berechnung des Modus oder Modalwerts zur Beschreibung von kategorialen Daten gibt es in R keine eigene Funktion. Um den Modus zu bestimmen, müssen wir zunächst herausfinden, welche Ausprägung die größte Häufigkeit aufweist. Aus der Tabelle in Abschnitt Abschnitt 2.1.1 können wir schon sehen, dass es nur einen einzigen Modus gibt, also nur eine Messwertausprägung, die die größte Häufigkeit aufweist. Gäbe es zwei (oder mehr) Ausprägungen mit der selben maximalen Häufigkeit, liefert der Code unten entsprechend mehrere Ergebnisse. Zunächst brauchen wir wieder die Häufigkeitstabelle mit table(), bestimmen das Maximum und wählen dann die Ausprägung(en) aus der Häufigkeitstabelle mit der maximalen Häufigkeit:
H <- table(neo_dat$HighestEducation) ## Häufigkeitstabelle erstellen
maximum <- max(H) ## das Objekt maximum enthält nun die größte(n) Häufigkeit(en).
which(H == maximum) ## mit which können wir die Ausprägungen von H erhalten, die die größte Häufigkeit aufweisenFachabitur_Abitur
2 Median und Quantile
Den Median können wir mit der Funktion median() berechnen.
median(neo_dat$Age)[1] 27Analog können wir auch beliebige Quantile mit quantile() berechnen. Per Default erhalten wir Quartile, das Minium und das Maximum. Über das zweite Argument, probs können wir definieren, welche Quantile wir wissen wollen.
Minimum (0 %), Quartilsgrenzen (25 %, 50 %, 75 %) und das Maximum (100 %):
quantile(neo_dat$Age) 0% 25% 50% 75% 100%
16 23 27 36 71 Dezile mit Minimum und Maximum erhalten wir, indem wir probs entsprechend definieren:
quantile(neo_dat$Age, probs = c(0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1)) 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100%
16 21 22 24 25 27 30 33 39 46 71 (Arithmetischer) Mittelwert
Den Mittelwert einer Variable können Sie mit mean() bestimmen.
mean(neo_dat$Age)[1] 30.72261Streuungsmaße
Empirische Varianz und Standardabweichung
Die wichtigsten Streuungsmaße empirische Varianz und empirische Standardabweichung sind definiert als:
\[\begin{align*} \text{Varianz: } &s_{emp}^2 = \frac{1}{n}\sum_{i=1}^n (x_i - \bar{x})^2 \\ \text{Standardabweichung: } &s_{emp} = \sqrt{s_{emp}^2} = \sqrt{\frac{1}{n}\sum_{i=1}^n (x_i - \bar{x})^2} \end{align*}\]
In R gibt es leider keine Funktionen, die diese Streuungsmaße direkt berechnen.4 Deshalb müssen wir selbst die Formel in R umsetzen. Dabei verwenden wir die Funktion mean() zur Berechung von \(\bar{x}\) und length() für \(n\).
var <- sum((neo_dat$Age - mean(neo_dat$Age))^2) / length(neo_dat$Age)
var[1] 114.833sd <- sqrt(var)
sd[1] 10.71601Interquartilsabstand
Den Interquartilsabstand, also die Differenz zwischen dem dritten (75 %) und ersten (25 %) Quartil können wir über die Funktion IQR() herausfinden:
quantile(neo_dat$Age) ## Nochmal alle Quartile 0% 25% 50% 75% 100%
16 23 27 36 71 IQR(neo_dat$Age) ## Hier die Differenz[1] 13Maßzahlen zur Beschreibung von Zusammenhängen zwischen Variablen
Kovarianz und Korrelation
Um den Zusammenhang von zwei Variablen zu beschreiben, kann die Korrelation direkt mit dem Befehl cor() berechnet werden. Ähnlich wie bei der empirischen Standardabweichung und - Varianz gibt es auch bei der Kovarianz keinen direkten Befehl um sie zu berechnen.5 Die Korrelation zwischen dem Alter und der Neurotizismus-Variablen N1 ist beispielsweise:
cor(neo_dat$Age, neo_dat$N1) ## Korrelation[1] -0.07388637Grafische Veranschaulichung mit einem Scatterplot
Zusammenhänge zwischen zwei Variablen können am besten mit einem Scatterplot veranschaulicht werden. Am Einfachsten geht das mit plot(). Hier geben Sie als erstes Argument die Variable an, die auf der x-Achse abgetragen werden soll und als zweites Argument die Variable der y-Achse. Zusätzlich können Sie noch viele weitere Veränderungen vornehmen, z.B. mit main einen Titel festlegen oder mit xlab und ylab die Beschriftung der x- und y-Achse.
plot(neo_dat$Age, neo_dat$N1,
main = 'Zusammenhang zwischen Age und N1',
xlab = 'Alter',
ylab = 'Item N1')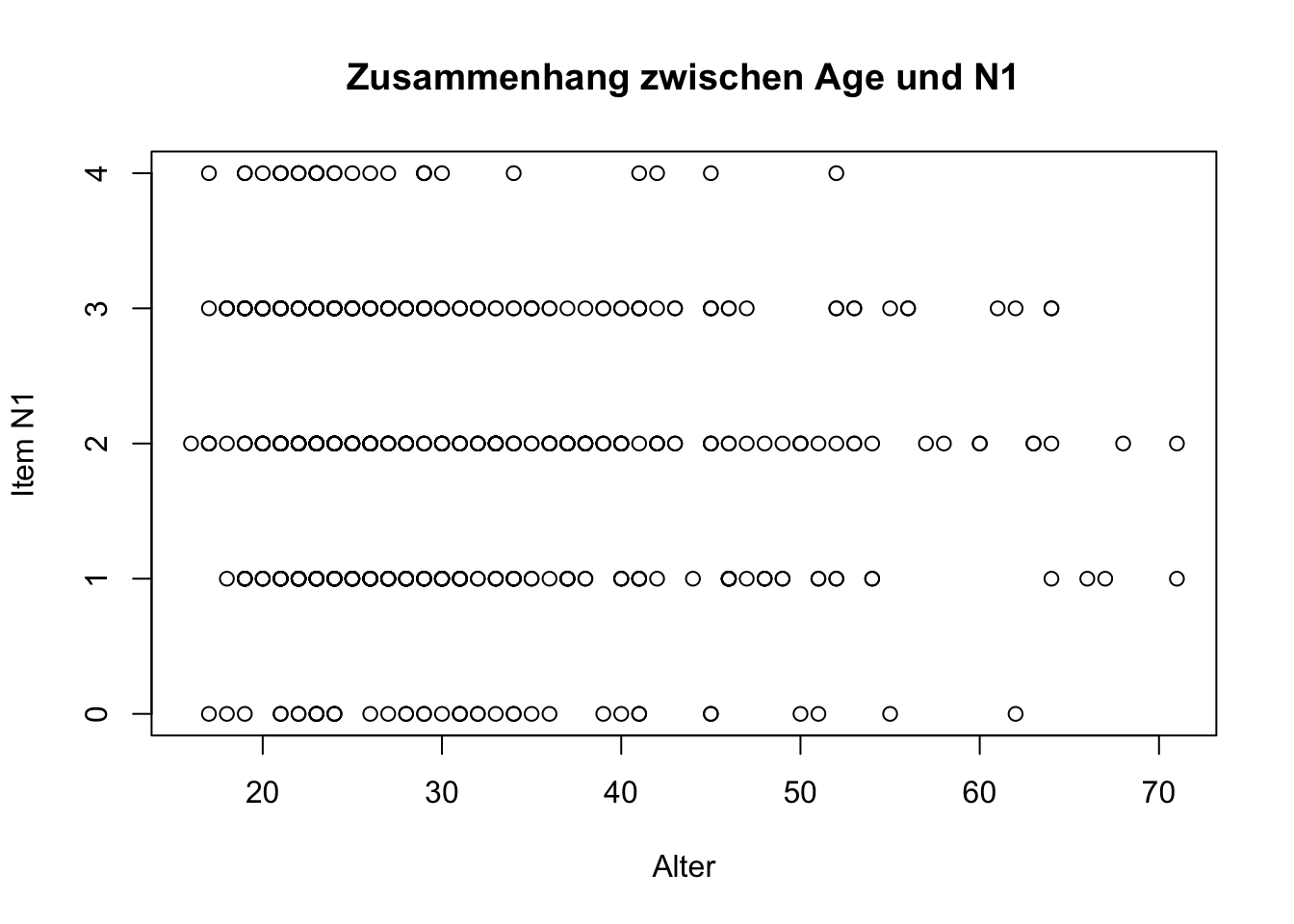
Beachten Sie, dass das Item N1 nur als ganze Zahl von 0 - 4 beantwortet werden konnte, entsprechend gibt es im Plot auch keine Zwischenwerte und die Punkte sind alle auf parallelen Linien angeordnet. Wenn das für die zweite Variable genauso ist (also z.B. wenn es auch ein Fragebogenitem wäre), dann ist das Plot so nicht sonderlich übersichtlich. Alternative Darstellungen finden Sie in Abschnitt Abschnitt 3.3.
2.2 Wahrscheinlichkeits(dichte)funktionen und Verteilungsfunktionen
Für viele gängige Verteilungen gibt es in R Funktionen um Wahrscheinlichkeits(dichte)funktion, Verteilungsfunktion, Quantilsfunktion und einen Zufallsgenerator zu nutzen.
Binomialverteilung
Am Beispiel einer Binomialverteilung mit \(n = 3\) und \(\pi = \frac{1}{6}\) können Sie mit dbinom() die Wahrscheinlichkeitsfunktion \(f(x)\) für einen bestimmten Wert x bestimmen.
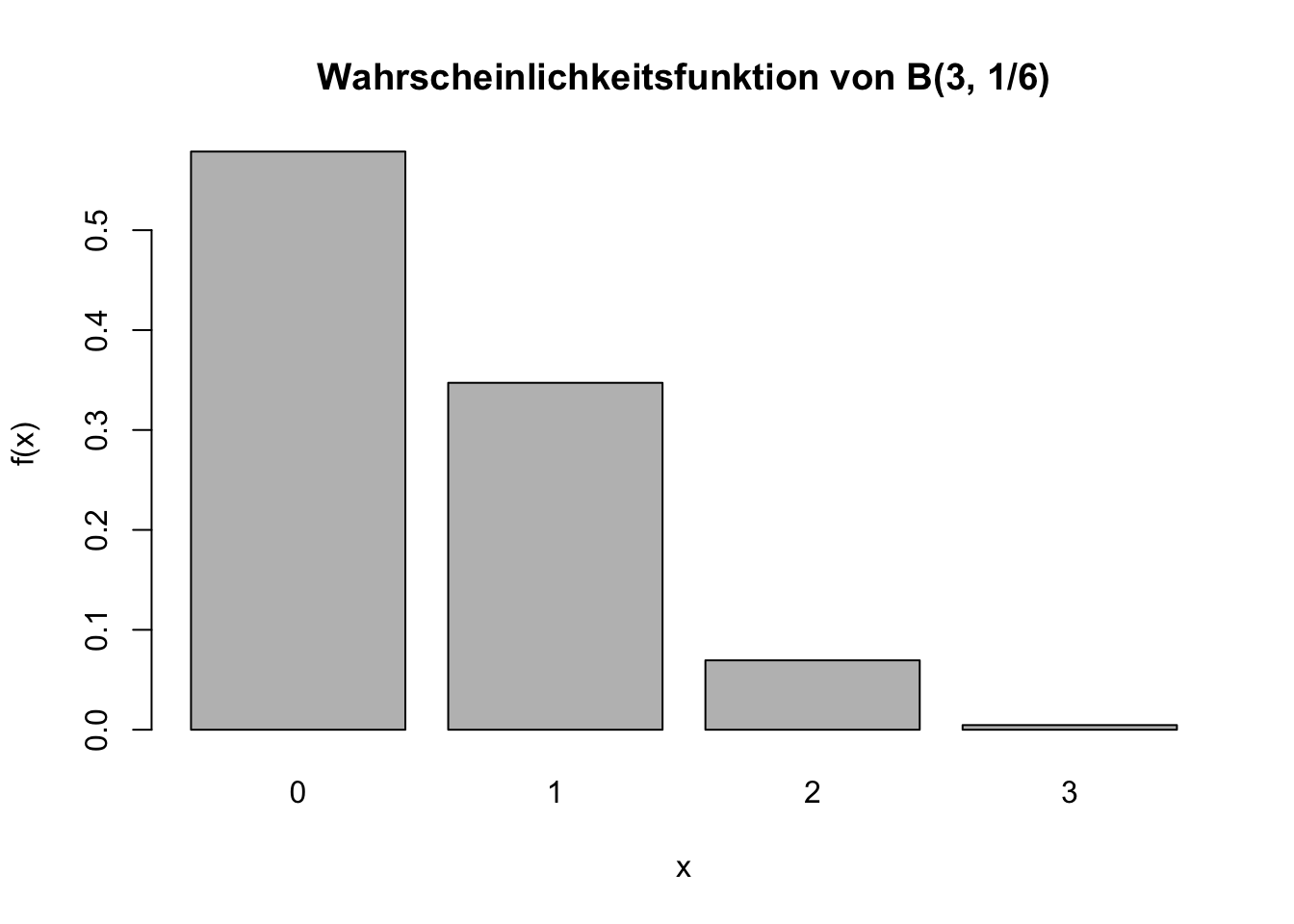
Wenn wir also den Wert für \(f(1)\) wissen wollen, verwenden wir:
dbinom(x = 1, size = 3, prob = 1/6)[1] 0.3472222Die Verteilungsfunktion \(F(x)\) erhalten wir mit pbinom(). Für die Bestimmung von \(F(2)\) verwenden wir:
pbinom(q = 2, size = 3, prob = 1/6)[1] 0.9953704und erhalten damit die Wahrscheinlichkeit \(P(X \le 2) = 0.995\) für diese spezifische Verteilung.
Die Quantilsfunktion qbinom() ist die Umkehrfunktion der Verteilungsfunktion. Die Frage \(P(X \le 2) = ?\) können wir mit der Verteilungsfunktion oben beantworten. Wenn jedoch die gegeben Informationen genau umgekehrt sind, wir also die Frage \(P(X \le ?) = 0.995\) beantworten wollen, verwenden wir:
qbinom(p = 0.995, size = 3, prob = 1/6)[1] 2und erfahren damit, dass bei einer gegebenen Wahrscheinlichkeit von \(p = 0.995\) Ausprägungen von 2 oder kleiner auftreten können.
Die Verteilungsfunktion und damit auch pbinom() ist immer die Repräsentation einer Wahrscheinlichkeit, dass sich die Zufallsvariable \(X\) in einem Wert kleiner oder gleich einem spezifischen Wert \(x_k\) realisiert. Wollen wir die Wahrscheinlichkeit für Realisationen größer einem spezifischen Wert \(x_k\), müssen wir uns zu Nutze machen, dass die Summe aller Wahrscheinlichkeiten 1 ist. Es gilt also
\[ \begin{aligned} P(X > x_k) &= 1 - P(X \le x_k) \text{ , bzw.} \\ P(X \ge x_k) &= 1 - P(X \le x_{k-1}) \end{aligned} \] Im Fall von \(P(X \ge x_k)\) müssen wir von 1 die Summe aller Wahrscheinlichkeiten der Ausprägungen von X subtrahieren, die kleiner sind als \(x_k\), also \(P(X \le x_{k-1})\).
Beispiel:
\[ \begin{aligned} P(X \ge 2) &= 1-P(X \le 1) \\ &= 1 - F(1) \end{aligned} \]
1 - pbinom(q = 1, size = 3, prob = 1/6)[1] 0.07407407\[ P(X \ge 2) = 0.074 \]
Als vierte Hilfsfunktion für die Binomialverteilung ist mit rbinom() das zufällige Ziehen einer Zufallsvariable X aus einer gegebenen Verteilung möglich. Als Ergebnis erhalten wir beliebig viele zufällig gezogene Realisationen der Zufallszahl:
rbinom(n = 10, size = 3, prob = 1/6) [1] 1 0 0 1 0 2 0 2 0 0Bei einer so geringen Erfolgswahrscheinlichkeit von \(\frac16\) sollte die 0 die am häufigsten beobachtete Ausprägung sein, was sich hier nun auch (zufällig) so zeigt. Mithilfe der Funktion könnte man auch gut illustrieren, dass sich bei sehr häufiger Ziehung die relativen Häufigkeiten der beobachteten Ausprägungen der Wahrscheinlichkeitsfunktion annähern.
# 100000 Ziehungen aus der gleichen Verteilung:
x <- rbinom(n = 100000, size = 3, prob = 1/6)
# relative Häufigkeiten berechnen:
h <- table(x)/100000
# rel. Häufigkeiten anzeigen
barplot(h, xlab = 'x',
ylab = 'relative Häufigkeit',
main = '100000 Ziehungen',
names.arg = c('0', '1', '2', '3'))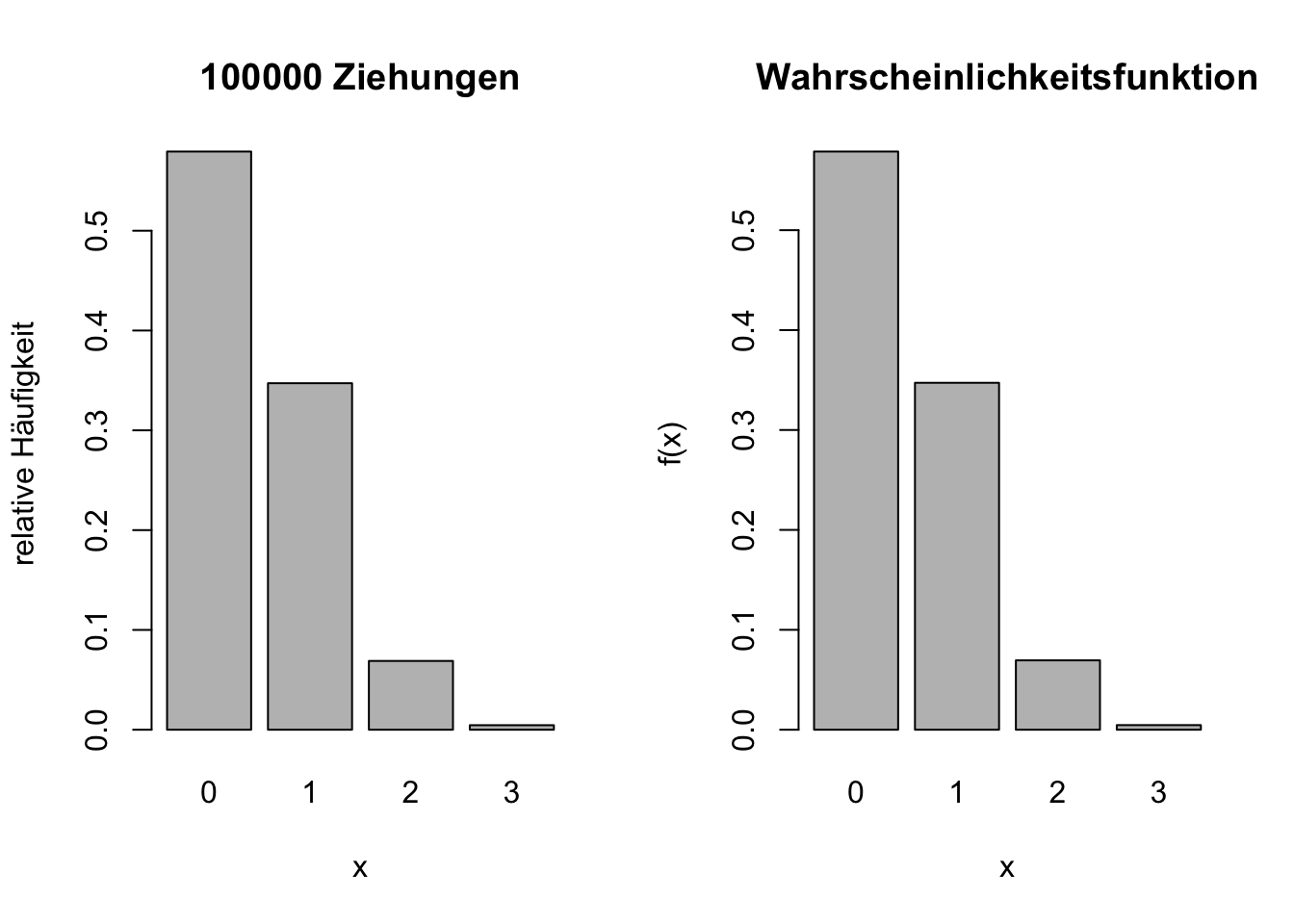
Normalverteilung
Genauso können wir für jede Normalverteilung die gleichen Funktionen mit dnorm(), pnorm(), qnorm() und rnorm() anwenden.
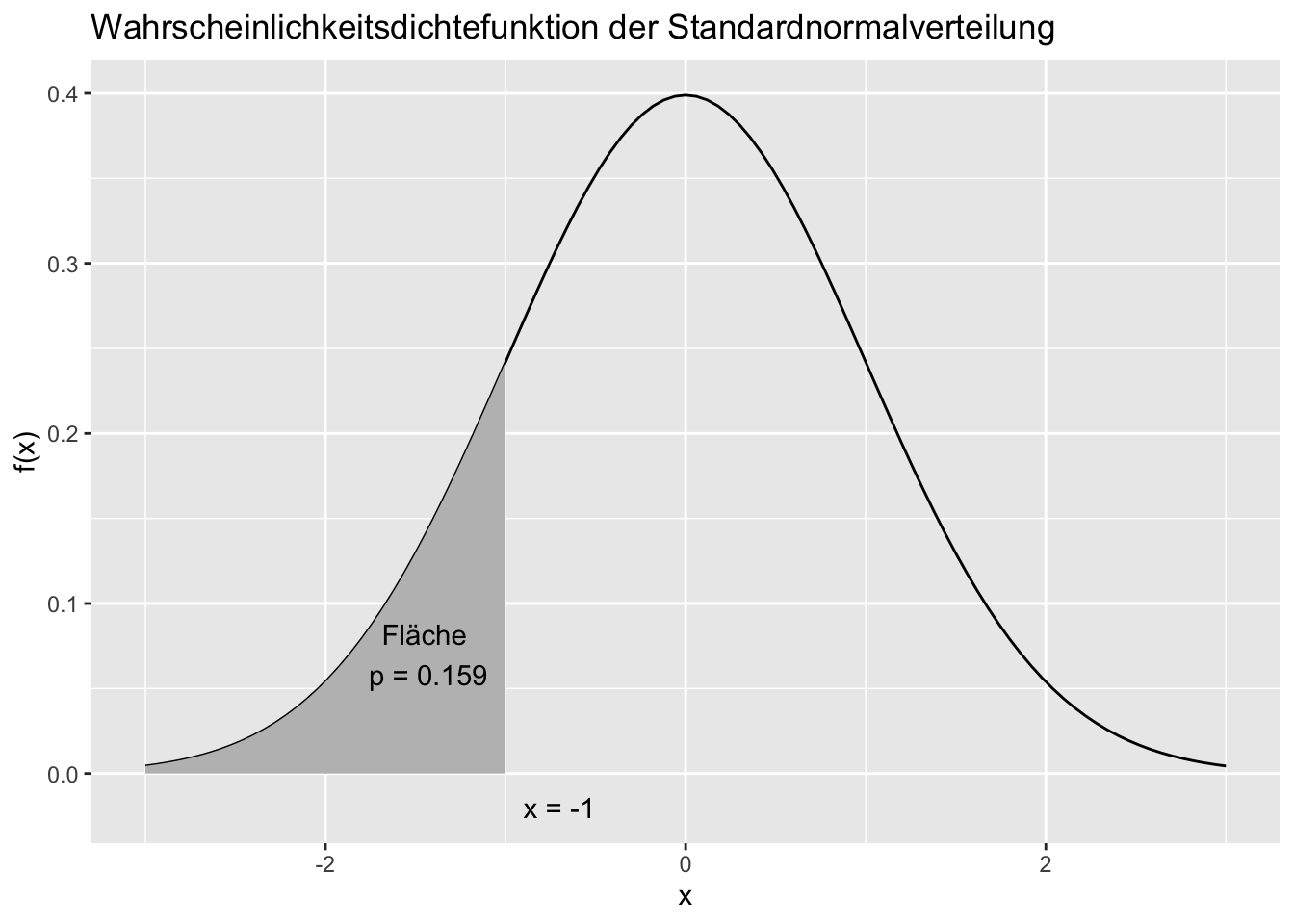
Häufig haben wir das Problem, dass wir wissen wollen, wie groß die Fläche unter \(f(x)\) links oder rechts von einem gegebenen Wert auf der x-Achse ist. Im obigen Beispiel würden wir erfahren, dass die Fläche für x-Werte von \(-\infty\) bis \(-1\) ca. \(0.159\) beträgt.
Diese Wahrscheinlichkeit \(P(X \leq -1)\), also dass in dieser spezifischen Verteilung Werte kleiner oder gleich -1 auftreten, können wir nun mit Hilfe der Verteilungsfunktion \(F(x)\) direkt bestimmen.
pnorm(q = -1, mean = 0, sd = 1)[1] 0.1586553Umgekehrt können wir wieder mit der Quantilsfunktion die Frage \(P(X \le ? ) = 0.159\) beantworten:
qnorm(p = 0.1586553, mean = 0, sd = 1) # ergibt gerundet 1[1] -0.9999998Die Verteilungsfunktion \(F(x)\) berechnet also die Fläche unter einer Wahrscheinlichkeitsdichtefunktion von \(- \infty\) bis zu einem bestimmten Wert. Die Quantilsfunktion ist die Umkehrfunktion dazu und beantwortet die Frage, an welcher Stelle wir die Wahrscheinlichkeitsdichtefunktion “abschneiden” müssten, damit die Fläche links davon (bis \(x = - \infty\)) eine gegebene Größe erreicht. Beachten Sie in der Abbildung, dass also bei Verteilungs- und Quantilsfunktion die Achsen einfach vertauscht sind.
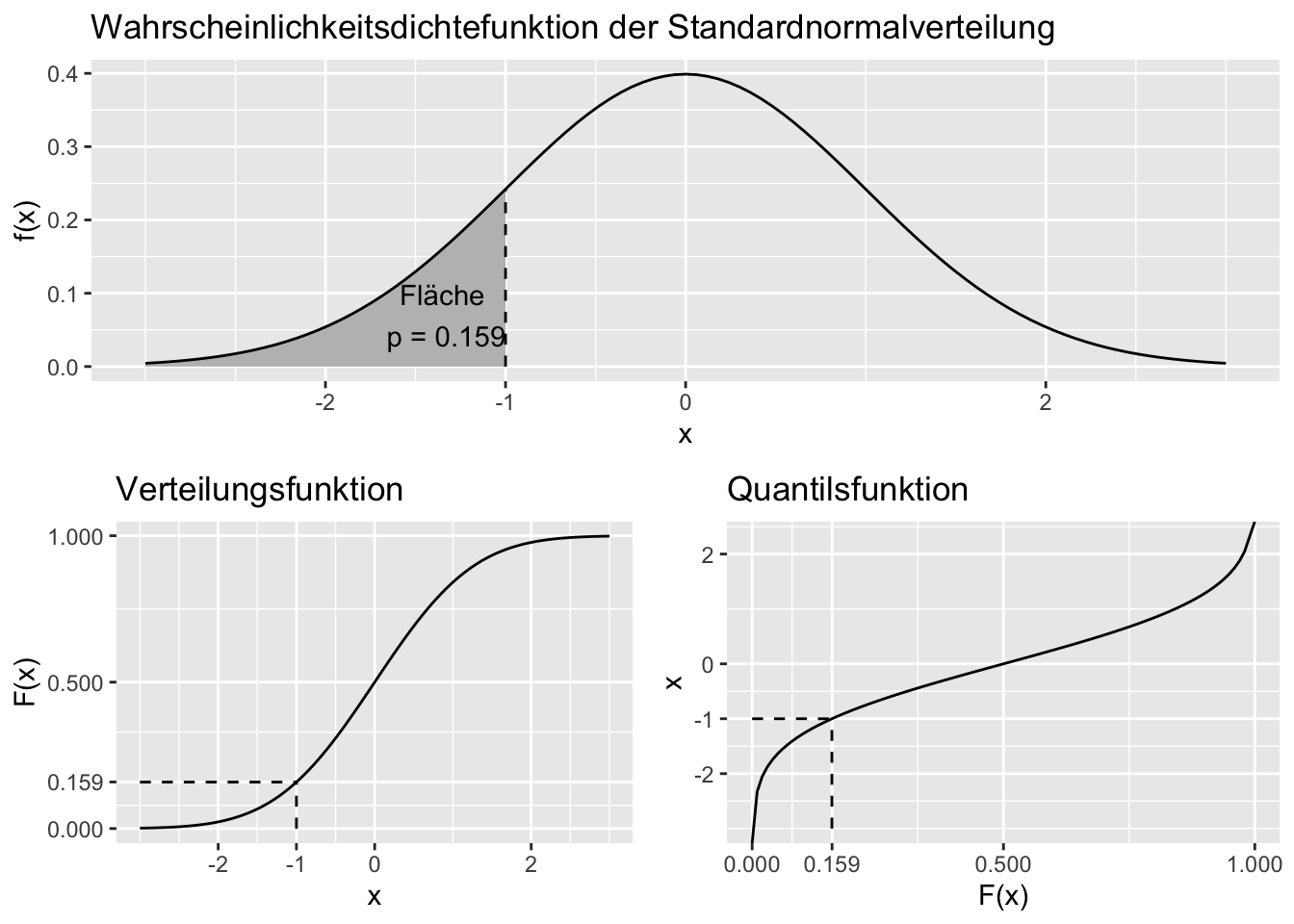
Für den Fall, dass uns eine Fläche rechts eines gegebenen Wertes unter der Funktion \(f(x)\) interessiert, müssen wir uns zu Nutze machen, dass (a) die gesamte Fläche unter der Wahrscheinlichkeitsdichtefunktion immer genau 1 ist und (b) \(P(X < -1) = P(X \le -1)\), da bei einer stetigen Verteilung wie der Normalverteilung \(P(X = -1) = 0\) ist (das natürlich nicht nur für die Ausprägung \(-1\) so, sondern für alle einzelnen Ausprägungen der Definitionsmenge).
\[ \begin{aligned} P(X \ge -1) &= 1 - P(X < -1) && \text{| } P(X < -1) = P(X \le -1) \\ &= 1 - P(X \le -1) \\ &= 1 - F(-1) \end{aligned} \]
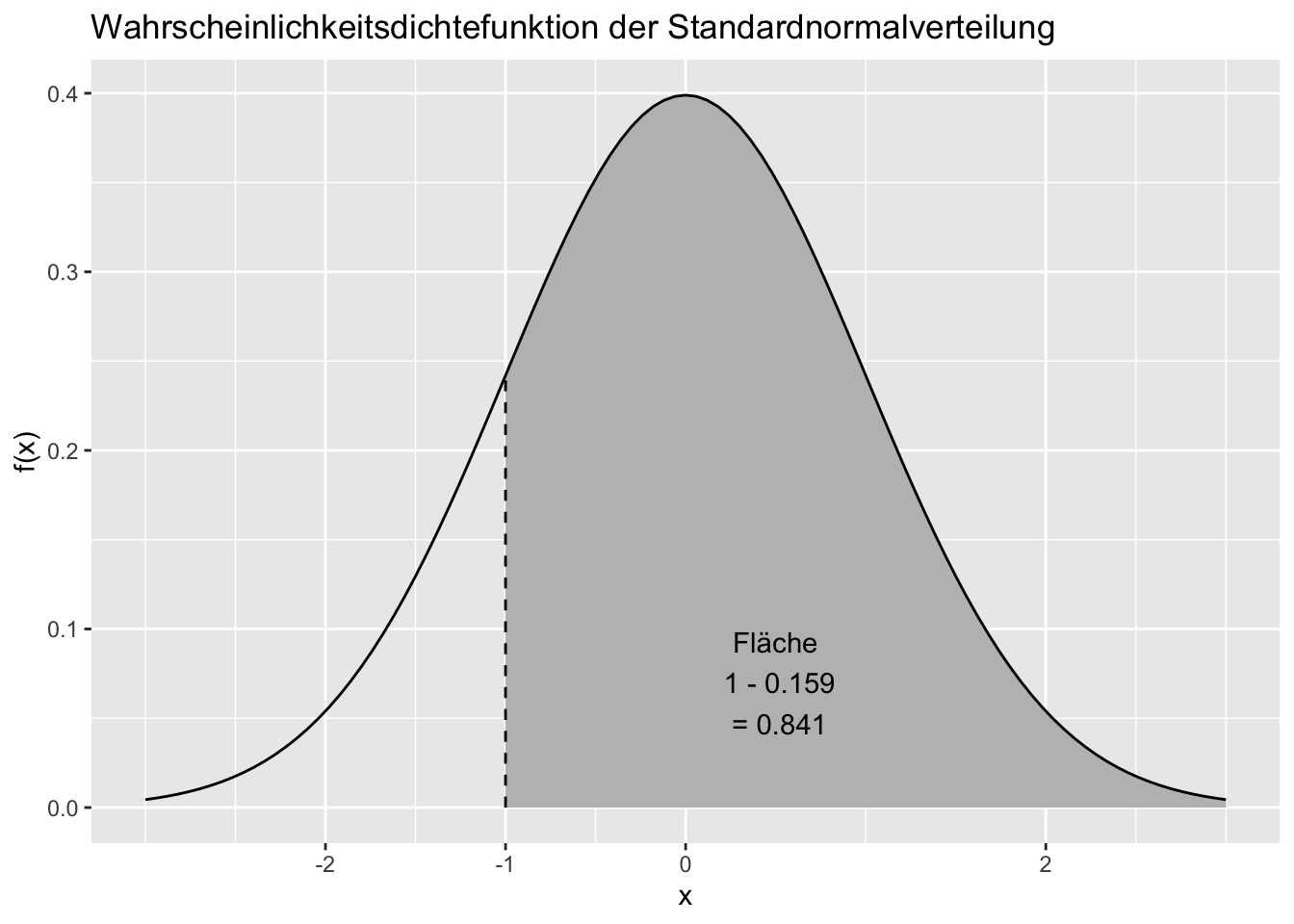
1 - pnorm(-1, mean = 0, sd = 1)[1] 0.8413447t-Verteilung
Die t-Verteilung ist wie die Normalverteilung oben eine stetige Verteilung. Die Erklärungen der dazu gehörigen Funktionen für die Normalverteilung können Sie also hier analog anwenden. Wie oben gibt es folgende Funktionen:
| Bezeichnung | r-Funktion |
|---|---|
| Wahrscheinlichkeitsdichtefunktion | dt() |
| Verteilungsfunktion | pt() |
| Quantilsfunktion | qt() |
| Zufällige Ziehungen | rt() |
2.3 Schätzung von Populationsgrößen
Häufigkeit eines Merkmals
Ist nach der Häufigkeit eines Merkmals (z.B. eine Eigentschaft liegt bei einer Person vor bzw. nicht vor) in einer Population gesucht, kann über eine gezogene einfache Zufallsstichprobe versucht werden, diese Größe zu schätzen. Ist also entsprechend jede einzelne Ziehung \(X_i\) verteilt mit \(X_i \sim Be(\pi)\), entspricht der Paramter \(\pi\) der Häufigkeit des Merkmals. Um den unbekannten Parameter \(\pi\) zu schätzen können wir mit den Daten der Stichprobe
die relative Häufigkeit des Merkmals in der Stichprobe \(h(1) = \bar{x}\) als Punktschätzer, und
das Konfidenzintervall um den Punktschätzer als Intervallschätzer verwenden.
Am Beispiel des Datensatzes neo_dat können wir zum Beispiel aus der Information der angegebenen Muttersprache (GermanAsNativeLanguage) schätzen, wie viele Personen in der Population aus der die vorliegende Stichprobe zufällig gezogen wurde, Deutsch als Muttersprache sprechen. Mit dem table() Befehl erhalten wir zunächst die Information, wie die Häufigkeitsverteilung in der Stichprobe ist:
table(neo_dat$GermanAsNativeLanguage)
no yes
24 542 Mit dem Befehl BinomCI() aus dem Paket DescTools (Signorell 2024) können wir nun Punkt- und Intervallschätzung vornehmen:
library(DescTools)
BinomCI(x = 542, # Häufigkeit der Kategorie 'Yes'
n = 566, # Anzahl der Personen i. d. Stichprobe
conf.level = 0.95, # gewünschtes Konfidenzniveau
method = 'wald') # gewünschte Approximation über Wald-Methode est lwr.ci upr.ci
[1,] 0.9575972 0.9409964 0.974198Die Schätzung des Parameters \(\pi\) und damit der Häufigkeit des Merkmals in der Population beträgt also 0.959. Im Intervall \(KI_{0.95} = [0.943, 0.976]\) befinden sich plausible Werte für den Parameter und die Häufigkeit des Merkmals.
Mittelwert und Mittelwertsunterschiede
Interessieren wir uns für Mittelwerte stetiger Merkmale, deren jeweilige Häufigkeitsverteilung in der Population gut durch eine Normalverteilung modelliert werden kann, können wir auch hier eine Schätzung aus den Stichprobendaten vornehmen. In diesem Fall entspricht der zu schätzende Populationsmittelwert \(\bar{x}\) dem Parameter \(\mu\) der Verteilung. Entsprechend werden Mittelwertsunterschiede \(\bar{x}_{1} - \bar{x}_{2}\) modelliert durch \(\mu_1 - \mu_2\).
Mittelwert einer Population (eine Stichprobe)
Wenn wir uns beispielsweise für die mittlere Ausprägung von Neurotizismus in der Population interessieren, können wir mit Hilfe der Stichprobendaten und der t-Verteilung Punkt- und Intervallschätzungen vornehmen. Während wir als Schätzfunktion für den Parameter einfach den Mittelwert der Stichprobe verwenden (\(\hat{\mu} = \bar{X}\)) können, benötigen wir die Schätzung eines Konfidenzintervalls zusätzlich Informationen der Verteilung des Modells und eine Schätzung des Standardfehlers dieser Schätzfunktion \(\widehat{SE}(X)\). Der Befehl zur Testung von Hypothesen (siehe späteres Kapitel Abschnitt 2.4.2) bei t-verteilten Zufallsvariablen t.test() kann uns hier weiterhelfen:
t.test(neo_dat$Neuro, # welche Variable interessiert uns
alternative = 'two.sided', # KIs sind üblicherweise symmetrisch, also "Zweiseitig"
conf.level = 0.95) # Konfidenzniveau
One Sample t-test
data: neo_dat$Neuro
t = 61.052, df = 565, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
1.866830 1.990944
sample estimates:
mean of x
1.928887 Die ersten Angaben können wir ignorieren (da sie den Hypothesentest betreffen, um den es hier nicht geht). Wichtig sind für uns die letzten Angaben:
95 percent confidence interval:
1.866830 1.990944
sample estimates:
mean of x
1.928887 Wir schätzen also den gesuchten Parameter \(\mu\) und damit die mittlere Ausprägung von Neurotizismus auf den Wert 1.929. Im Intervall \(KI_{0.95} = [1.867, 1.991]\) liegen plausible Werte für den Parameter und damit die durchschnittliche Ausprägung von Neurotizismus.
Unterschiede der Mittelwerte zweier abhängiger Stichproben
Häufig haben wir Forschungsfragen, die den Unterschied von zwei Mittelwerten aus abhängigen Stichproben betreffen. Abhängige Stichproben liegen beispielsweise bei einem Vorher-Nachher-Vergleich vor, bei dem eine Variable vor einer Intervention (Prä) und danach (Post) erhoben wurde. Der mittlere Unterschied Prä-Post beantwortet dann z.B. die Frage, welche Veränderung durch die Intervention zu erwarten ist.
Da im Beispieldatensatz keine solche Erhebung erfasst wurde, sehen wir uns als Beispiel die (nicht unbedingt sinnvolle) Frage an, wie groß der mittlere Unterschied zwischen Extraversion und Neurotizismus von Personen ist. Als Beispiel für eine abhängige Stichprobe eignet sich diese Frage deshalb, weil von jeder Person paarweise Informationen über Extraversion und Neurotizismus vorliegen.
Auch für eine solche Fragestellung können wir den Befehl t.test() verwenden. Wir müssen hier nur die Information über die zweite interessierende Variable ergänzen und angeben, dass wir von abhängigen (“paired”) Stichproben ausgehen. Die restlichen Argumente sind identisch wie oben im Einstichprobenfall. Für die Punkt- und Intervallschätzung ist wieder nur der untere Teil des Outputs interessant.
t.test(neo_dat$Neuro, # Werte der "ersten" Messung
neo_dat$Extra, # Werte der "zweiten" Messung
paired = TRUE, # Es sollen abhängige Stichproben sein
alternative = "two.sided", # Two.sided weil symmetrisches KI
conf.level = 0.95) # unser übliches Konfidenzniveau
Paired t-test
data: neo_dat$Neuro and neo_dat$Extra
t = -6.5925, df = 565, p-value = 9.939e-11
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
-0.4097153 -0.2216157
sample estimates:
mean difference
-0.3156655 Wir schätzen also die gesuchte Paramteterdifferenz \(\mu_{Neuro} - \mu_{Extra}\) und damit die Ausprägung des mittleren Unterschieds der Ausprägungen von Neurotizismus und Extraversion von Personen auf die Differenz der Stichprobenmittelwerte \(\bar{x}_{Neuro} - \bar{x}_{Extra} = -0.316\). Im Intervall \(KI_{0.95} = [-0.410, -0.222]\) liegen plausible Werte für die Parameterdifferenz und damit die durchschnittliche Differenz der Mittelwerte in der Population.
Die Differenz der Mittelwerte und der Mittelwert der Differenzen ist im Fall von Wertepaaren identisch, da \[ \begin{aligned} \bar{X}_{Diff} &= \frac{1}{n} \sum\limits_{i = 1}^{n}X_{Diff_i} = \\ &= \frac{1}{n} \sum\limits_{i = 1}^{n} (X_{1_i}-X_{2_i}) = \\ &= \frac{1}{n} (\sum\limits_{i = 1}^{n} X_{1_i}-\sum\limits_{i = 1}^{n}X_{2_i}) = \\ &= \frac{1}{n} \sum\limits_{i = 1}^{n} X_{1_i}-\frac{1}{n} \sum\limits_{i = 1}^{n}X_{2_i} = \\ &= \bar{X_1} - \bar{X_2} \end{aligned} \]
Unterscheide zwischen Mittelwerten zweier unabhängiger Populationen
Interessiert uns der Unterschied zweier Mittelwerte bei unabhängigen Stichproben, können wir ebenfalls den t.test()-Befehl verwenden . Im Beispiel interessiert uns der Unterschied der durchschnittlichen Neurotizismuswerte von Personen die 30 Jahre oder älter sind, im Vergleich zu jüngeren Personen. Wir können hier wie im Fall der abhängigen Stichproben die Messwerte beider Gruppen als erstes und zweites Argument verwenden und das Argument paired = FALSE setzen.
t.test(neo_dat[neo_dat$Age < 30, "Neuro"], # Werte der ersten Gruppe
neo_dat[neo_dat$Age >= 30, "Neuro"], # Werte der zweiten Gruppe
paired = FALSE, # unabhängige Stichproben
var.equal = TRUE, # Annahme gleicher Varianzen in der Population
alternative = "two.sided", # symmetrisches KI
conf.level = 0.95) # Konfidenzniveau
Two Sample t-test
data: neo_dat[neo_dat$Age < 30, "Neuro"] and neo_dat[neo_dat$Age >= 30, "Neuro"]
t = 2.1104, df = 564, p-value = 0.03527
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.009339889 0.260297159
sample estimates:
mean of x mean of y
1.985101 1.850282 Wir schätzen also die gesuchte Paramteterdifferenz \(\mu_{juenger} - \mu_{aelter}\) und damit die Ausprägung des Unterschieds der mittleren Ausprägungen von Neurotizismus in den beiden Gruppen auf die Differenz der Stichprobenmittelwerte \(\bar{x}_{juenger} - \bar{x}_{aelter} = 1.985 - 1.850 = 0.135\). Im Intervall \(KI_{0.95} = [0.009, 0.260]\) liegen plausible Werte für die Parameterdifferenz und damit die Differenz der Mittelwerte beider Populationen.
Alternative über die Formelschreibweise
Liegt jedoch die interessierende Variable in einer Spalte und die Information über die Gruppenzugehörigkeit in einer anderen Spalte des Datensatzes vor, können wir auch eine andere Form der Syntax verwenden. Hierzu erstellen wir erst mit dem Befehl cut() eine Hilfsvariable, die die Information enthält, ob eine Person 30 oder älter ist, oder ob sie jünger ist.
neo_dat$ueber30 <- cut(neo_dat$Age, # die Variable basiert auf Age
breaks = c(0, 30, 100), # Minimum, Grenze, Maximum
labels = c("juenger", "aelter"),# Benennung der Gruppen
right = FALSE) # damit zählt die Grenze 30 zur aelter-GruppeNun liegt eine Variable vor, die genau zwei Ausprägungen hat und jede Beobachtung der Gesamtstichprobe in eine von genau zwei Gruppen einteilt. Damit könnten wir nun innerhalb des Befehls t.test() die Formelschreibweise verwenden.
Diese wird nach dem Schema links ~ rechts erstellt. Links der Tilde (~) steht der Name der Spalte, deren Mittelwerte wir berechnen möchten, und rechts der Tilde die Variable, die die Information über die beiden Gruppen enthält.
Wichtig: Wir verwenden innerhalb der Formel nur die Namen der Spalten! Der Name des data.frames, aus dem die Spalten stammen, wird extra als neues Argument data = angegeben. Das Argument paired = FALSE ist nun überflüssig, da die Variante des Befehls mit der Formelschreibweise ausschließlich unabhängige Stichproben behandeln kann.
t.test(Neuro ~ ueber30, # Formel UV ~ Gruppe
data = neo_dat, # data.frame der die Variablen enthält
var.equal = TRUE, # Annahme gleicher Varianzen der Populationen
alternative = "two.sided", # symmetrisch
conf.level = 0.95) # Konfidenzniveau
Two Sample t-test
data: Neuro by ueber30
t = 2.1104, df = 564, p-value = 0.03527
alternative hypothesis: true difference in means between group juenger and group aelter is not equal to 0
95 percent confidence interval:
0.009339889 0.260297159
sample estimates:
mean in group juenger mean in group aelter
1.985101 1.850282 Das geschätzte Konfidenzintervall ist identisch mit dem oberen. Welche Variante wir wählen ist also Geschmackssache oder hängt davon ab, wie die Variablen im Datensatz vorliegen. Z.B. erscheint das Erstellen der Hilfsvariable ueber30 umständlich, wenn die Aufteilung der Gruppen wie oben gezeigt auch gleich direkt über die Variable Age erfolgen kann.
Liegt jedoch eine Gruppierungsvariable schon im Datensatz vor, wie beispielsweise eine Variable Treatment die angibt, ob eine Person der Experimental oder Kontrollgruppe zugeordnet wird, ist die zuletzt gezeigte Variante mit der Formelschreibweise praktischer.
Cohens \(\delta\) als Effektstärke
Mittelwertsunterschiede so wie wir sie im vorigen Abschnitt berechnet haben, haben den Nachteil, dass sie nicht unabhängig sind von der Einheit des Messinstruments, das der Untersuchung zu Grunde liegt. Der geschätzte Unterschied der Mittelwerte von Älteren und Jüngeren in Neurotizismus beispielsweise hängt in seiner Höhe maßgeblich davon ab, ob das Persönlichkeitsinventar mit dem Neurotizismus erhoben wurde die Ausprägungen in Werten zwischen 1 - 5 ermittelt oder von 0 - 100. Da unter anderem das die Vergleichbarkeit von Studienergebnissen mit unterschiedlichen Messmethoden erschwert, gibt es standardisierte Maße (auch Effektstärke oder Effektgröße genannt), die Effekte wie Mittelwertsunterschiede unabhägig von Einheit und Streuung eines Merkmals ermitteln und Vergleiche über Studien und Messinstrumente hinweg erlauben.
Für den Fall von Mittelwertsunterschieden erlaubt die Effektstärke Cohens \(\delta\) solche Vergleiche. \(\delta\) ist dabei definiert als
\[ \begin{align} \text{für unabhängige Stichproben: } \delta &= \frac{\mu_1 - \mu_2}{\sqrt{\sigma}}\\ \text{für abhängige Stichproben: } \delta &= \frac{\mu_1 - \mu_2}{\sqrt{\sigma_{Diff}}} \end{align} \]
Für Schätzungen von \(\delta\) können nun entsprechende Schätzfunktionen für \(\mu_1\), \(\mu_2\), \(\sigma\) bzw. \(\sigma_{Diff}\) eingesetzt werden. In R können wir \(\hat{\delta}\) mit der Funktion smd() aus dem MBESS Pakets berechnen. Hierfür müssen wir nur auf die Daten der beiden Gruppen, die wir miteinander vergleichen wollen, zugreifen.
library(MBESS)
smd(neo_dat[neo_dat$ueber30 == 'juenger', 'Neuro'],
neo_dat[neo_dat$ueber30 == 'aelter', 'Neuro'])[1] 0.1799103Konfidenzintervalle erhalten wir dann mit Hilfe der gerade berechneten Schätzung von \(\delta\) und dem Befehl ci.smd() aus dem gleichen Paket. Zusätzlich ist die Angabe der beiden Gruppengrößen notwendig. Dafür sehen wir uns in einem ersten Schritt mit table() an, wie viele Personen jünger und älter als 30 sind.
table(neo_dat$ueber30)
juenger aelter
330 236 ci.smd(smd = 0.1799, # aus smd() oben
n.1 = 330, # n Gruppe 'juenger'
n.2 = 236, # n Gruppe 'aelter'
conf.level = 0.95) # Konfidenzniveau$Lower.Conf.Limit.smd
[1] 0.01240396
$smd
[1] 0.1799
$Upper.Conf.Limit.smd
[1] 0.3472372Auf Basis dieses Intervalls sind also Werte zwischen 0.012 und 0.347 plausible Werte für die Effektstärke \(\delta\).
Es gibt viele verschiedene Varianten von Cohens \(\delta\), je nach Studiendesign und Fragestellung. Für eine Schätzung von \(\delta\) in anderen Designs (z.B. Mittelwertsunterschiede abhängiger Gruppen) gibt es z.B. im Paket effsize passende Funktionen.
Stichprobenplanung für Konfidenzintervalle
Planen wir eine Studie mit dem Ziel, Mittelwertsunterschiede zu schätzen, sollten wir vor der Datenerhebung eine Stichprobenplanung durchführen. Die Stichprobenplanung beantwortet die Frage, wie groß unsere Stichprobe(n) sein sollte(n), um die Populationsgröße mit einer bestimmten vorgegebenen Genauigkeit zu schätzen.
Das Maß für die Genauigkeit ist hier die erwartete Länge (\(E(O-U)\)) eines Konfidenzintervalls mit einem vorgegebenen Konfidenzniveau (meistens \(1 - \alpha = 0.95\)). Aus technischen Gründen müssen wir die Stichprobenplanung für die standardisierte Effektgröße (\(\delta\)) durchführen, wir besprechen also hier nur für die Fälle, in denen Mittelwertsunterschiede kontinuierlicher Variablen in der Population geschätzt werden sollen.
Zur Berechnung der Stichprobengröße ist es außerdem notwendig, eine Annahme über den wahren Effekt in der Population zu treffen. Je größer der angenommene wahre Effekt (\(\delta\)), desto größer die benötigte Stichprobengröße für eine bestimmte erwartete Länge des Konfidenzintervalls (Achtung, das ist sehr unintuitiv!). Um ganz sicher zu geben kann es daher sinnvoll sein, einen mittleren bis großen Effekt vorzugeben (auch wenn die benötigte Stichprobengröße bei Konfidenzintervallen nicht besonders stark von der angenommenen Effektgröße abhängt). Für die Frage, welche Werte für die erwartete Länge sinnvoll sind, siehe die Überlegungen in den Veranstaltungsmaterialien.
Wir führen die Stichprobenplanung in R mit der Funktion ss.aipe.smd im MBESS Paket durch. Der Befehl funktioniert für die Fälle mit zwei unabhängigen und zwei abhängigen Stichproben genau gleich. Man beachte jedoch, dass \(\delta\) in beiden Fällen unterschiedlich definiert ist.
library(MBESS)
ss.aipe.smd(delta = 0.5, # angenommene wahre Effektgröße
conf.level = 0.95, # gewünschtes Konfidenzniveau
width = 0.29) # gewünschte erwartete Länge des KIs[1] 377WICHTIG: Der ausgegebene Wert entspricht der Stichprobengröße pro Gruppe.
2.4 Testen von Hypothesen
In diesem Kapitel beschäftigen wir uns mit statistischen Hypothesentests. Wir verwenden dazu die gleichen Daten wir im Kapitel zur Schätzung von Populationsgrößen.
Häufigkeit eines Merkmals
Zuerst testen wir Hypothesen bezüglich einer relativen Häufigkeit in der Population. Wir testen die Hypothese, dass mehr als die Hälfte der Personen in der Population die Muttersprache Deutsch haben (d.h. wir glauben die relative Häufigkeit der Muttersprache Deutsch in der Population ist größer als 0.5). Wir testen also die folgenden statistischen Hypothesen: \[H_0: \pi \leq 0.5; H_1: \pi > 0.5\] Der entsprechende Hypothesentest heißt auch Binomialtest und kann in R mit dem Befehl binom.test() durchgeführt werden.
binom.test(x = 542, # Häufigkeit der Kategorie 'Yes'
n = 566, # Anzahl der Personen i. d. Stichprobe
p = 0.5, # pi_0 unter der Nullhypothese
alternative = "greater") # Art/Richtung der Alternativhypothese
Exact binomial test
data: 542 and 566
number of successes = 542, number of trials = 566, p-value < 2.2e-16
alternative hypothesis: true probability of success is greater than 0.5
95 percent confidence interval:
0.9408827 1.0000000
sample estimates:
probability of success
0.9575972 Der Wert x = 542 entspricht der Häufigkeit der Kategorie “Yes” in der Variable neo_dat$GermanAsNativeLanguage. Die Anzahl der Personen in der Stichprobe entspricht n = 566. Der Wert \(\pi_0\), gegen den in der Nullhypothese getestet wird, ist hier mit p = 0.5 angegeben. Die Alternativhypothese kann ungerichtet (alternative = "two.sided"), linksgerichtet ("less"), oder wie in unserem Beispiel rechtsgerichtet ("greater") getestet werden.
Wichtig für die Testentscheidung ist nur der p-Wert, den wir der Ausgabe entnehmen und mit unserem selbst gewählten Signifikanzniveau (\(\alpha = 0.005\)) vergleichen. Da 2.2e-16 \(= 2.2 \cdot 10^{-16} < 0.005\) gilt, ist der p-Wert kleiner als das Signifikanzniveau und wir entscheiden uns für die Alternativhypothese, dass mehr als die Hälfte der Personen in der Population die Muttersprache Deutsch haben.
Mittelwerte und Mittelwertsunterschiede
Mittelwert einer Population (eine Stichprobe)
Nun wollen wir Hypothesen bezüglich des Mittelwert einer stetigen Variable in einer Population testen. Wir testen die Hypothese, dass sich die durchschnittliche Ausprägung im (stetigen) Neurotizismus in der Population vom Wert 0 unterscheidet (kein inhaltlich sinnvolles Beispiel). Wir testen also die folgenden statistischen Hypothesen: \[H_0: \mu = 0; H_1: \mu \neq 0\] Der entsprechende Hypothesentest heißt auch Einstichproben-t-Test und kann in R mit dem Befehl t.test() durchgeführt werden.
t.test(neo_dat$Neuro, # welche Variable interessiert uns
mu = 0, # mu_0 unter der Nullhypothese
alternative = 'two.sided') # Art/Richtung der Alternativhypothese
One Sample t-test
data: neo_dat$Neuro
t = 61.052, df = 565, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
1.866830 1.990944
sample estimates:
mean of x
1.928887 Als erstes übergeben wir den Vektor mit den Neurotizismuswerten in der Stichprobe (neo_dat$Neuro). Der Wert \(\mu_0\), gegen den in der Nullhypothese getestet wird, ist hier mit mu = 0 angegeben. Die Alternativhypothese kann linksgerichtet (alternative = "less"), rechtsgerichtet ("greater") oder wie in unserem Beispiel ungerichtet ("two.sided") getestet werden.
Der Output enthält neben dem \(p-Wert\), den wir für die Testentscheidung mit unserem selbst gewählten Signifikanzniveau (\(\alpha = 0.005\)) vergleichen müssen, auch den beobachteten Wert der Teststatistik \(t\) und die entsprechenden Freiheitsgrade \(df\). Da 2.2e-16 \(= 2.2 \cdot 10^{-16} < 0.005\) gilt, ist der p-Wert kleiner als das Signifikanzniveau und wir entscheiden uns für die Alternativhypothese, dass sich der durchschnittliche \(Neurotizismus\) in der Population vom Wert 0 unterscheidet.
Unterschiede der Mittelwerte zweier abhängiger Stichproben
Im nächsten Beispiel geht es um Hypothesen bezüglich Unterschieden in Mittelwerten stetiger Variablen bei abhängigen Stichproben. Wir testen die Hypothese, dass der mittlere (stetige) Neurotizismus von Personen in der Population höher ist als deren mittlere (stetige) Extraversion (kein inhaltlich sinnvolles Beispiel). Wir testen also die folgenden statistischen Hypothesen: \[H_0: \mu_1 - \mu_2 \leq 0; H_1: \mu_1 - \mu_2 > 0\] Der entsprechende Hypothesentest heißt auch Zweistichproben-t-Test für abhängige Stichproben und kann in R mit dem Befehl t.test() durchgeführt werden.
t.test(neo_dat$Neuro, # Werte der "ersten" Messung
neo_dat$Extra, # Werte der "zweiten" Messung
mu = 0, # mu_0 unter der Nullhypothese
paired = TRUE, # Es sollen abhängige Stichproben sein
alternative = "greater") # Art/Richtung der Alternativhypothese
Paired t-test
data: neo_dat$Neuro and neo_dat$Extra
t = -6.5925, df = 565, p-value = 1
alternative hypothesis: true mean difference is greater than 0
95 percent confidence interval:
-0.3945548 Inf
sample estimates:
mean difference
-0.3156655 Als erstes übergeben wir den Vektor mit den Neurotizismuswerten (neo_dat$Neuro) und den Vektor mit den Extraversionswerten (neo_dat$Extra) aus der gleichen Stichprobe. Der Wert \(\mu_0\), gegen den in der Nullhypothese getestet wird, wird hier mit mu = 0 angegeben. Das Argument paired = TRUE bedeutet, dass es sich hier um den Test für zwei abhängige Stichproben handelt. Die Alternativhypothese kann ungerichtet (alternative = "two.sided"), linksgerichtet ("less") oder wie in unserem Beispiel rechtsgerichtet ("greater") getestet werden.
Der Hypothesentest rechnet für die Teststatistik immer Mittelwert der als erstes übergebenen Werte minus Mittelwert der als zweites übergebenen Werte (\(\bar{x}_1 - \bar{x}_2\)). Damit der Test die richtige Hypothese testet, ist es also wichtig, dass die Reihenfolge der übergebenen Werte mit der unter alternative spezifizierten Richtung der Alternativhypothese abgestimmt ist.
Der Output enthält neben dem \(p-Wert\), den wir für die Testentscheidung mit unserem selbst gewählten Signifikanzniveau (\(\alpha = 0.005\)) vergleichen müssen, auch den beobachteten Wert der Teststatistik \(t\) und die entsprechenden Freiheitsgrade \(df\). Da \(1 > 0.005\) gilt, ist der p-Wert größer als das Signifikanzniveau und wir entscheiden uns für die Nullhypothese, dass der mittlere Neurotizismus von Personen in der Population niedriger oder genauso hoch ist als deren mittlere Extraversion.
Unterscheide zwischen Mittelwerten zweier unabhängiger Populationen
Im nächsten Beispiel geht es um Hypothesen bezüglich Unterschieden in Mittelwerten stetiger Variablen in zwei unabhängigen Stichproben. Hier verwenden wir die Variable Neuro$ueber30 aus Abschnitt Abschnitt 2.3.2.3. Wir testen die Hypothese, dass der mittlere (stetige) Neurotizismus von Personen in der Population unter 30 Jahren niedriger ist als in der Population über 30 Jahren. Wir testen also die folgenden statistischen Hypothesen: \[H_0: \mu_1 - \mu_2 \geq 0; H_1: \mu_1 - \mu_2 < 0\] Der entsprechende Hypothesentest heißt auch Zweistichproben-t-Test für unabhängige Stichproben und kann in R mit dem Befehl t.test() durchgeführt werden.
t.test(neo_dat[neo_dat$ueber30 == "juenger", "Neuro"], # Werte der ersten Gruppe
neo_dat[neo_dat$ueber30 == "aelter", "Neuro"], # Werte der zweiten Gruppe
mu = 0,
paired = FALSE,
var.equal = TRUE,
alternative = "less")
Two Sample t-test
data: neo_dat[neo_dat$ueber30 == "juenger", "Neuro"] and neo_dat[neo_dat$ueber30 == "aelter", "Neuro"]
t = 2.1104, df = 564, p-value = 0.9824
alternative hypothesis: true difference in means is less than 0
95 percent confidence interval:
-Inf 0.2400704
sample estimates:
mean of x mean of y
1.985101 1.850282 Als erstes übergeben wir den Vektor mit den Neurotizismuswerten der Stichprobe unter 30 Jahren (neo_dat[neo_dat$ueber30 == "juenger", "Neuro"]) und den Vektor mit den Neurotizismuswerten der Stichprobe über 30 Jahren (neo_dat[neo_dat$ueber30 == "aelter", "Neuro"]). Der Wert \(\mu_0\), gegen den in der Nullhypothese getestet wird, wird hier mit mu = 0 angegeben. Das Argument paired = FALSE bedeutet, dass es sich hier um den Test für zwei unabhängige Stichproben handelt. Das Argument var.equal = TRUE trifft die für den t-Test für zwei unabhängige Stichproben typische Modellannahme, dass sich die Varianz im Neurotizismus in den beiden Populationen nicht unterscheidet. Die Alternativhypothese kann ungerichtet (alternative = "two.sided"), rechtsgerichtet ("greater") oder wie in unserem Beispiel linksgerichtet ("less") getestet werden.
Der Hypothesentest rechnet für die Teststatistik immer Mittelwert der als erstes übergebenen Werte minus Mittelwert der als zweites übergebenen Werte (\(\bar{x}_1 - \bar{x}_2\)). Damit der Test die richtige Hypothese testet, ist es also wichtig, dass die Reihenfolge der übergebenen Werte mit der unter alternative spezifizierten Richtung der Alternativhypothese abgestimmt ist.
Der Output enthält neben dem \(p-Wert\), den wir für die Testentscheidung mit unserem selbst gewählten Signifikanzniveau (\(\alpha = 0.005\)) vergleichen müssen, auch den beobachteten Wert der Teststatistik \(t\) und die entsprechenden Freiheitsgrade \(df\). Da \(0.9824 > 0.005\) gilt, ist der p-Wert größer als das Signifikanzniveau und wir entscheiden uns für die Nullhypothese, dass der durchschnittliche \(Neurotizismus\) in der Population unter 30 Jahre höher oder genauso hoch ist als in der Population über 30 Jahre.
Neben der gerade gezeigten Möglichkeit, die Werte aus beiden Stichproben als separate Vektoren zu übergeben, gibt es auch noch die folgende alternative R-Syntax (ebenfalls möglich beim Zweistichproben-t-Test für abhängige Stichproben in Abschnitt 2.3.2.3). Diese macht sich wieder die Formelschreibweise zu Nutze, die in Abschnitt Abschnitt 3.3.1 eingeführt wurde.
t.test(Neuro ~ ueber30, # Formel UV ~ Gruppe
data = neo_dat, # data.frame der die Variablen enthält
mu = 0, # mu_0 unter der Nullhypothese
var.equal = TRUE, # Annahme gleicher Varianzen
alternative = "less") # Art/Richtung der Alternativhypothese
Two Sample t-test
data: Neuro by ueber30
t = 2.1104, df = 564, p-value = 0.9824
alternative hypothesis: true difference in means between group juenger and group aelter is less than 0
95 percent confidence interval:
-Inf 0.2400704
sample estimates:
mean in group juenger mean in group aelter
1.985101 1.850282 Ein Vorteil dieser Syntax ist, dass der R-Output übersichtlicher beschriftet ist. Es lässt sich sofort erkennen, dass \(\bar{x}_1\) (so wie hier die Daten übergeben wurden) für den mitteren Neurotizismus in der Stichprobe unter 30 steht und \(\bar{x}_2\) für den mitteren Neurotizismus in der Stichprobe über 30. Da der Hypothesentest in der Formel für die Teststatistik immer \(\bar{x}_1 - \bar{x}_2\) rechnet, lässt sich damit einfach überprüfen, ob die im Befehl unter alternative spezifizierte Richtung der Alternativhypothese tatsächlich der interessierenden Hypothese entspricht. Natürlich lässt es sich theoretisch beeinflussen, welche Ausprägung der Variable ueber30 als \(\bar{x}_1\) verwendet wird, es ist jedoch häufig praktikabler, den Befehl einfach durchzuführen und ggf. im Nachhinein die Richtung der Alternativhypothese (von "less" zu "greater" oder umgekehrt) zu ändern.
Stichprobenplanung für Hypothesentests
Planen wir eine Studie mit dem Ziel, eine Hypothese bzgl. Mittelwerten oder Mittelwertsunterschieden zu testen, sollten wir vor der Datenerhebung eine Stichprobenplanung durchführen. Die Stichprobenplanung beantwortet die Frage, wie groß unsere Stichprobe(n) sein sollte(n), damit der geplante Hypothesentest eine vorgegebene Genauigkeit aufweist.
Das Maß für die Genauigkeit ist hier die Power mit einem vorgegebenen Signifikanzniveau (meistens \(\alpha = 0.005\)). Aus technischen Gründen müssen wir die Stichprobenplanung für die standardisierte Effektgröße (\(\delta\)) durchführen, wir besprechen also hier nur für die Fälle, in denen Hypothesen über Mittelwerte kontinuierlicher Variablen in der Population getestet werden sollen.
Zur Berechnung der Stichprobengröße ist es außerdem notwendig, eine Annahme über den wahren Effekt in der Population zu treffen. Je kleiner der angenommene Effekt unter der Alternativhypothese \(\delta_{H_1}\) (Achtung: \(\delta_{H_1}\) ist nicht das gleiche wie der wahre Effekt in der Population \(\delta\)), desto größer die benötigte Stichprobengröße für eine bestimmte Power des Hypothesentests (Achtung, das ist anders herum als bei der Stichprobenplanung für KIs). Um ganz sicher zu geben kann es daher sinnvoll sein, einen kleinen Effekt vorzugeben (im Gegensatz zur Stichprobenplanung bei Konfidenzintervallen hat bei Hypothesentests die angenommene Effektgröße einen starken Einfluss auf die benötigte Stichprobengröße).
Wir führen die Stichprobenplanung in R mit der Funktion pwr.t.test im pwr Paket durch. Der Befehl kann für die Fälle mit einer Stichprobe, zwei unabhängigen Stichproben und zwei abhängigen Stichproben verwendet werden. Man beachte jedoch, dass \(\delta_{H_1}\) in den drei Fällen unterschiedlich definiert ist.
library(pwr)
pwr.t.test(power = 0.8, # gewünschte Power des Hypothesentests
d = 0.2, # angenommene wahre Effekt unter H1
sig.level = 0.005, # gewünschtes Signifikanzniveau
type = 'two.sample', # Art des Hypothesentests
alternative = 'greater') # Art/Richtung der Alternativhypothese
Two-sample t test power calculation
n = 585.6093
d = 0.2
sig.level = 0.005
power = 0.8
alternative = greater
NOTE: n is number in *each* groupDie Argumente bedeuten:
powerist die gewünschte Power des Hypothesentests (\(1-\beta\))dist der angenommene Effekt unter der Alternativhypothese (\(\delta_{H_1}\))sig.levelist das gewünschte Signifikanzniveau (\(\alpha\))typeist die Art des Hypothesentests; möglich sindone.sample(Einstichproben t-Test),two.sample(Zweistichproben t-Test für unabhängige Stichproben) undpaired(Zweistichproben t-Test für abhängige Stichproben)alternativeist die Art/Richtung der Alternativhypothese und entspricht dem gleichnamigen Argument in dert.testFunktion; möglich sindless(linksgerichtete H1),greater(rechtsgerichtete H1) undtwo.sided(ungerichtete H1)
Wichtig: Sie müssen alle Argumente explizit mit dem jeweiligen Namen und = angeben.
Ergebnis: Im Output können Sie unter n die mindestens benötigte Stichprobengröße ablesen (da Sie keine halben Personen erheben können, macht es Sinn, selbst auf die nächste ganze Zahl aufzurunden):
- Beim Einstichproben t-Test entspricht dies einfach der Stichprobengröße.
- Beim Zweistichproben t-Test für abhängige Stichproben entspricht dies der Stichprobengröße pro Messzeitpunkt (abhängiger Gruppe).
- Bei Zweistichproben t-Test für unabhängige Stichproben entspricht dies der Stichprobengröße pro Stichprobe (also \(n_1\) bzw. \(n_2\)).
Poweranalyse für Hypothesentests
Die bei der Stichprobenplanung für Hypothesentests verwendete Funktion pwr.t.test aus dem pwr Paket kann auch dazu verwendet werden, um für eine bestimmte vorgegeben Stichprobengröße \(n\), unter Angabe des angenommenen Effekts unter der Alternativhypothese (\(\delta_{H_1}\)) und des Signifikanzniveau (\(\alpha\)) die Power (\(1 - \beta\)) des Hypothesentests zu berechnen.
library(pwr)
pwr.t.test(n = 100, # vorgegebene Stichprobengröße pro Gruppe
d = 0.2, # angenommene wahre Effekt unter H1
sig.level = 0.005, # gewünschtes Signifikanzniveau
type = 'two.sample', # Art des Hypothesentests
alternative = 'greater') # Art/Richtung der Alternativhypothese
Two-sample t test power calculation
n = 100
d = 0.2
sig.level = 0.005
power = 0.1203114
alternative = greater
NOTE: n is number in *each* groupMit dem Argument n geben Sie eine bestimmte Stichprobengröße vor:
- Beim Einstichproben t-Test entspricht dies einfach der Stichprobengröße.
- Beim Zweistichproben t-Test für abhängige Stichproben entspricht dies der Stichprobengröße pro Messzeitpunkt (abhängiger Gruppe).
- Bei Zweistichproben t-Test für unabhängige Stichproben entspricht dies der Stichprobengröße pro Stichprobe (also \(n_1\) bzw. \(n_2\)). Das heißt, Sie können die Power nur für gleiche Stichprobengrößen \(n_1 = n_2\) bestimmen.
Die anderen Argumente bedeuten das gleiche wie im Kapitel zur Stichprobenplanung bei Hypothesentests beschrieben.
Wichtig:
- Sie müssen alle Argumente explizit mit dem jeweiligen Namen und = angeben.
- Bei linksgerichteten Alternativhypothesen (
alternative = less) muss der mit dem Argumentdangegebene Effekt ein negatives Vorzeichen haben (sonst ergibt die berechnete Power keinen Sinn).
Ergebnis: Im Output können Sie unter power die Power eines wie angegeben durchgeführten Hypothesentests ablesen.
3 Nützliche Funktionen
3.1 Daten aufbereiten
Variablen (Spalten) auswählen
Um Variablen eines Datensatzes auszuwählen - um beispielsweise für eine Analyse nur ein bestimmtes Subset an Variablen zu verwenden - können wir
zunächst definieren, welche Variablen wir auswählen wollen (z.B. über deren Namen oder Position im Datensatz)
den Datensatz indizieren, also nur die in a. definierten Variablen auswählen
ggf. den in b. indizierten Datensatz einem neuen Objekt zuweisen:
Möglichkeit 1 - mit Bordmitteln in R
Die grundlegendste Variante klappt schon mit Bordmitteln, also ohne Installation weiterer Pakete.
# Vektor mit den Namen aller Extraversions-Items:
vars <- c("E1", "E2", "E3", "E4", "E5", "E6", "E7", "E8", "E9", "E10", "E11", "E12")
# Indizieren des Datensatzes mit [..., ...]
# Vor dem Komma werden Zeilen ausgewählt
# Nach dem Komma werden Spalten ausgewählt.
extraversion_dat <- neo_dat[, vars]Möglichkeit 2 - mit Hilfe des Pakets dplyr
Das Paket dplyr bietet uns mit dem Befehl select() eine schöne Möglichkeit, Variablen auszuwählen.
library(dplyr)
vars <- c("E1", "E2", "E3", "E4", "E5", "E6", "E7", "E8", "E9", "E10", "E11", "E12")
extraversion_dat <- select(neo_dat, all_of(vars)) #1. Argument: data.frame; 2. Argument: VariablennamenDie Zuweisung zu einem neuen Objekt extraversion_dat ist nicht unbedingt nötig. Wenn wir auf den reduzierten Datensatz zugreifen möchten, können wir auch immer wieder die Indizierung über [] oder select() anwenden.
Variablen umkodieren
Wenn Sie einzelne Variablen im Datensatz haben, die inhaltlich umgekehrt kodiert zu allen anderen Variablen sind, sollten Sie für weitere Analysen sicherstellen, dass diese auch im Datensatz umkodiert sind. Wenn Sie in einem Befragungstool wie SoSciSurvey bei Erstellung der entsprechenden Frage bereits angegeben haben, dass die Variable umgekehrt kodiert ist, sorgt das Tool in der Regel bereits dafür, dass auch die Zahlenwerte umkodiert werden (z.B. statt Werte von 0 - 4, Werte von 4 - 0).
Wenn Sie keine solche Angabe gemacht haben oder die Daten händisch erfasst haben, müssen Sie die Variablen selbst umkodieren. Die Variablen im Beispieldatensatz sind von Null (0) bis Vier (4) kodiert, entsprechend könnte eine Differenz schon zum gewünschten Ergebnis führen:
| Rohwert | Operation | Umkodierter Wert |
|---|---|---|
| 0 | 4 - 0 | 4 |
| 1 | 4 - 1 | 3 |
| 2 | 4 - 2 | 2 |
| 3 | 4 - 3 | 1 |
| 4 | 4 - 4 | 0 |
Die Operation \(4 - \text{Rohwert} = \text{Umkodierter Wert}\) ist also eine einfache Möglichkeit die Umkodierung vorzunehmen.6 Um also die Umkodierung für ein einzelnes Items (im Beispiel Item E1) vorzunehmen und dieses neue Item dann gleich dem Datensatz hinzuzufügen, können wir das über folgenden Weg machen
## die Differenz wird durchgeführt und das Ergebnis einer neuen Variable E1_r im Datensatz hinzugefügt:
neo_dat$E1_r <- 4 - neo_dat$E1 Die neue Variable E1_r ist nun umgekehrt kodiert. Überprüfen können wir das, indem wir aus dem Datensatz das Original und die umkodierte Variante auswählen und anzeigen:
select(neo_dat, E1, E1_r) E1 E1_r
1 3 1
2 0 4
3 4 0
4 2 2
5 3 1
6 0 4
7 2 2
8 3 1
9 3 1
10 2 2Mittelwerte über mehrere Variablen bilden
Für die Auswertung vieler Fragebogen ist es notwendig, für jede Person (= Zeile eines Datensatzes) eine Summe oder einen Mittelwert über mehrere Spalten hinweg zu bilden. In unserem Beispiel kann über den Mittelwert aller Antworten auf jedes einzelne Neurotizismusitem (alle Items die mit “N” beginnen) ein Indikator für die generelle Neurotizismusausprägung einer Person gebildet werden.7
Eine Möglichkeit, einen Mittelwert (“mean”) über eine ganze Zeile (“row”) hinweg zu bilden, ist der Befehl rowMeans(). Als Argument geben wir nicht den gesamten Datensatz an (da wir nicht über sämtliche Items einen Mittelwert bilden wollen), sondern wählen mit [] nur die Items aus, die zur Neurotizismusskala gehören.
neo_dat$Neuro <- rowMeans(neo_dat[, c("N1", "N2", "N3", "N4", "N5", "N6", "N7", "N8", "N9", "N10", "N11", "N12")])Die Verwendung bestimmter Befehle aus dem Paket dplyr (Wickham u. a. 2023) kann das Ganze ein bisschen übersichtlicher machen. Hier verwenden wir den Befehl select() um aus dem Datensatz nur bestimmte Spalten auszuwählen. Da die Benennung der Items einer ganz bestimmten Logik folgt, können wir für die Auswahl auch den Befehl num_range() verwenden.
Beispielsweise setzen sich die Bezeichnungen der Items der Extraversionsskala aus dem Buchstaben “E” und einer Zahl aufsteigend von 1 - 12 zusammen:
neo_dat$Extra <- rowMeans(select(neo_dat, num_range("E", 1:12)))Über beide Varianten haben wir nun die Variablen Neuro und Extra erstellt, die für jede Person des Datensatzes den Mittelwert der Neurotizismusitems bzw. der Extraversionsitems enthält.
3.2 Fehlende Werte
In R werden leere Zellen einer Tabelle in einem data.frame als Fehlende Werte (NA) kodiert. D.h. in diesesn Zellen steht nicht nichts, sondern NA. So ist für R repräsentiert, dass hier kein regulärer Eintrag, z.B. einer Zahl oder eines Wortes vorliegt. Die meisten Befehle um Daten zu organisieren oder analysieren haben Argumente, um mit möglicherweise vorliegenden NAs adäquat umzugehen. Es gibt mehrere Möglichkeiten, wie fehlende Werte in einen data.frame kommen können:
Keine Einträge in den Rohdaten Sofern in den eingelesenen Rohdaten bestimmte Zellen einfach leer sind, werden diese in R bereits automatisch als NA gekennzeichnet.
Einträge in den Rohdaten, die als Fehlende Werte definiert werden sollen Sofern Sie (z.B. in SoSciSurvey) bei der Erstellung einer Frage neben der üblichen Antwortskala noch weitere Option (z.B. “keine Beurteilung möglich”) angegeben haben, werden Antworten auf diesen Optionen in den Daten üblicherweise mit Werten wie z.B. “-1” oder “99” gekennzeichnet. Es gibt also mehrere Möglichkeiten, wie ein Item fehlende Informationen aufweisen kann.
Das Item wurde nicht beantwortet. Dann ist die Zelle in den Rohdaten leer und in R automatisch als
NAkodiert.Das Item wurde mit “keine Beurteilung möglich” beantwortet und in den Rohdaten mit einem Wert wie z.B. “-1” oder “99” kodiert. Für manche Analysen kann es dann sinnvoll sein, auch diese Ausprägungen als
NAs zu definieren, damit sie nicht berücksichtigt werden. Dafür verwenden wir aus demdplyr- Paket die Funktionen
mutate_at()- um nur bestimmte Spalten eines data.frames zu verändernvars()- um einfach über die Namen der Spalten eine Auswahl zu treffen, undna_if()- um bestimmte Werte in einNAumzuwandeln.
neo_dat <- mutate_at(.tbl = neo_dat, # Auswahl des data.frames
.vars = vars(E1:C12), # Auswahl der zu korrigierenden Variablen
.funs = list(~na_if(., 99))) # Jede 99 wird duch NA ersetztAusschluss von ProbandInnen mit fehlenden Werten
Fehlende Werte können z.B. dann sinnvoll verwendet werden, wenn entschieden werden soll, ob Personen aufgrund zu wenig beantworteter Items aus der Analyse ausgeschlossen werden sollen. Hierfür verwenden wir folgende Funktionen: - is.na() um herauszufinden, ob ein Wert NA ist oder nicht (TRUE/FALSE), - rowSums() um für jede Zeile (=Person) zu zählen, wie viele TRUE (= 1) vorkommen, - > um einen logischen Vergleich zu machen. Also z.B. abzufragen, ob die Summe der NAs eine definierte Schwelle übersteigt oder nicht - filter() um Personen auszuwählen, die die Schwelle unter- oder überschreiten.
AnzahlNAs <- rowSums(is.na(select(neo_dat, E1:C12))) # die neue Variable enthält für jede Zeile (Person) die Zahl der NAs
neo_dat_ohneNA <- filter(neo_dat, AnzahlNAs == 0) # nur wenn genau 0 NAs vorkommen, verbleibt die Zeile im neuen Datensatz neo_dat_ohneNAManche Befehle erfordern es, dass im gesamten data.frame kein einziger fehlender Wert vorkommt. Dies kann man einfacher als oben gezeigt mit dem Befehl na.omit() erreichen.
neo_dat_komplettOhneNA <- na.omit(neo_dat)Vorsicht: im ersten Ansatz werden nur Beobachtungen aus dem data.frame entfernt, die in den Variablen E1 - C12 (alle inhaltlich interessanten Variablen) mindestens einen fehlenden Wert aufweisen. Im zweiten Ansatz werden Beobachtungen entfernt, bei der in irgend einer Variable mindestens einen fehlenden Wert aufweisen. Im Gegensatz zum ersten Ansatz, könnte es also sein, dass eine Person aus dem Datensatz entfernt wird, nur weil sie in einer eigentlich nicht wichtigen Variable (z.B. beim Alter) keine Angaben gemacht hat, obwohl die restlichen Daten durchaus sinnvoll interpretierbar wären. Hier also immer genau abwägen, welche Variante der inhaltlichen Fragestellung der Analyse am dienlichsten ist.
Verwendung von Befehlen trotz vorliegender Fehlender Werte
Wenn fehlende Werte im Datensatz enthalten sind, kann es passieren, dass Befehle mit dem Datensatz nicht mehr so arbeiten wie wir es gewohnt sind. Ein Mittelwert z.B. kann für eine Reihe von Werten, bei denen (mindestens) ein NA enthalten ist, nicht berechnet werden. Wir können den entsprechenden Befehl mean() jedoch so anpassen, dass die NAs einfach ignoriert werden und der Mittelwert über die verbleibenden Werte berechnet wird. Die meisten Befehle haben dafür ein eigenes Argument. Bei mean() können wir beispielsweise das Argument na.rm = TRUE verwenden.
v <- c(1, 2, 3, NA, 4, 5, 6) ## Beispielvektor mit einem NA
mean(v) ## per Default kann mean() mit dem NA nichts anfangen.[1] NAmean(v, na.rm = TRUE) ## mit dem Argument na.rm = TRUE wird der NA vor Berechnung des Mittelwerts entfernt.[1] 3.5Wie das Argument heißt, mit dem Sie definieren können, wie mit Fehlenden Werten verfahren werden soll, finden Sie beispielsweise über die Hilfe (@ref(hilfe)) heraus. In der Hilfe zu mean() finden wir im Abschnitt Arguments folgende Information:

Hier lernen wir, dass das Argument na.rm das richtige macht wenn wir einen entsprechenden logischen Wert (TRUE/FALSE) angeben.
3.3 Plots
Streudiagramme
Streudiagramme (engl. Scatterplot) können wir mit dem äußerst vielseitigen plot()-Befehl erstellen. Dieser Befehl ist (so wie z.B. auch summary()) ein generischer Befehl, der je nachdem welche Daten als Argumente übergeben werden, ein unterschiedliches Verhalten zeigen kann.
Für ein Streudiagramm zwischen den Variablen N1 und E1 können wir beide Vektoren als Argumente übergeben. Zusätzlich können wir viele weitere Informationen als Argumente übergeben, die das Aussehen des Plots beeinflussen.
plot(neo_dat$N1, neo_dat$E1,
main = "Streudiagramm", # Titel
xlab = "N1", # Label der x-Achse
ylab = "E1") # Label der y-Achse
Alternativ können wir auch die so genannte Formelschreibweise verwenden. Hier müssen wir angeben welche Variable (linke Seite der Formel) wir auf der y-Achse in Abhängigkeit von welcher anderen Variable (rechte Seite der Formel) auf der x-Achse darstellen möchten. Beide Seiten der Formel werden durch eine ~ (gesprochen: Tilde) voneinander getrennt. Zusätzlich können wir in einer Formel auch direkt auf die Namen der Variablen zugreifen, ohne den Namen des data.frames mit $ voranzustellen. Dann müssen wir den data.frame jedoch nach der Formel angeben:
plot(E1 ~ N1, neo_dat)
Da beide Variablen nur diskrete Antworten kennen, sieht das Streudiagramm wenig aussagekräftig aus. Deshalb gibt es Befehle, die die einzelnen Punkte um einen zufälligen Betrag auf x und y-Achse verschieben (“jitter”), um Häufungen besser darzustellen. Am komfortabelsten klappt das mit dem Paket ggplot2 (siehe @ref(ggplot2)), das jedoch eine etwas andere Syntax verlangt.
Histogramme
Häufigkeitsverteilungen von diskreten und stetigen Variablen können mit Säulendiagrammen (auch: “Balkendiagramm”) bzw. Histogrammen am einfachsten dargestellt werden. Im Abschnitt @ref(balken-histogramme) zeigen wir das Vorgehen in R.
Boxplots
Verteilungen von Variablenantworten lassen sich mit Boxplots gut veranschaulichen. Wie bei plot() können wir mit zusätzlichen Argumenten die Grafik anschaulicher machen.
boxplot(neo_dat$N1,
main = 'Boxplot von N1')
Wenn wir Boxplots unterschiedlicher Gruppen miteinander vergleichen wollen, können wir die Variable in der die Gruppenzugehörigkeit hinterlegt ist mit Hilfe der Formelschreibweise angeben.
boxplot(N1 ~ GermanAsNativeLanguage, neo_dat)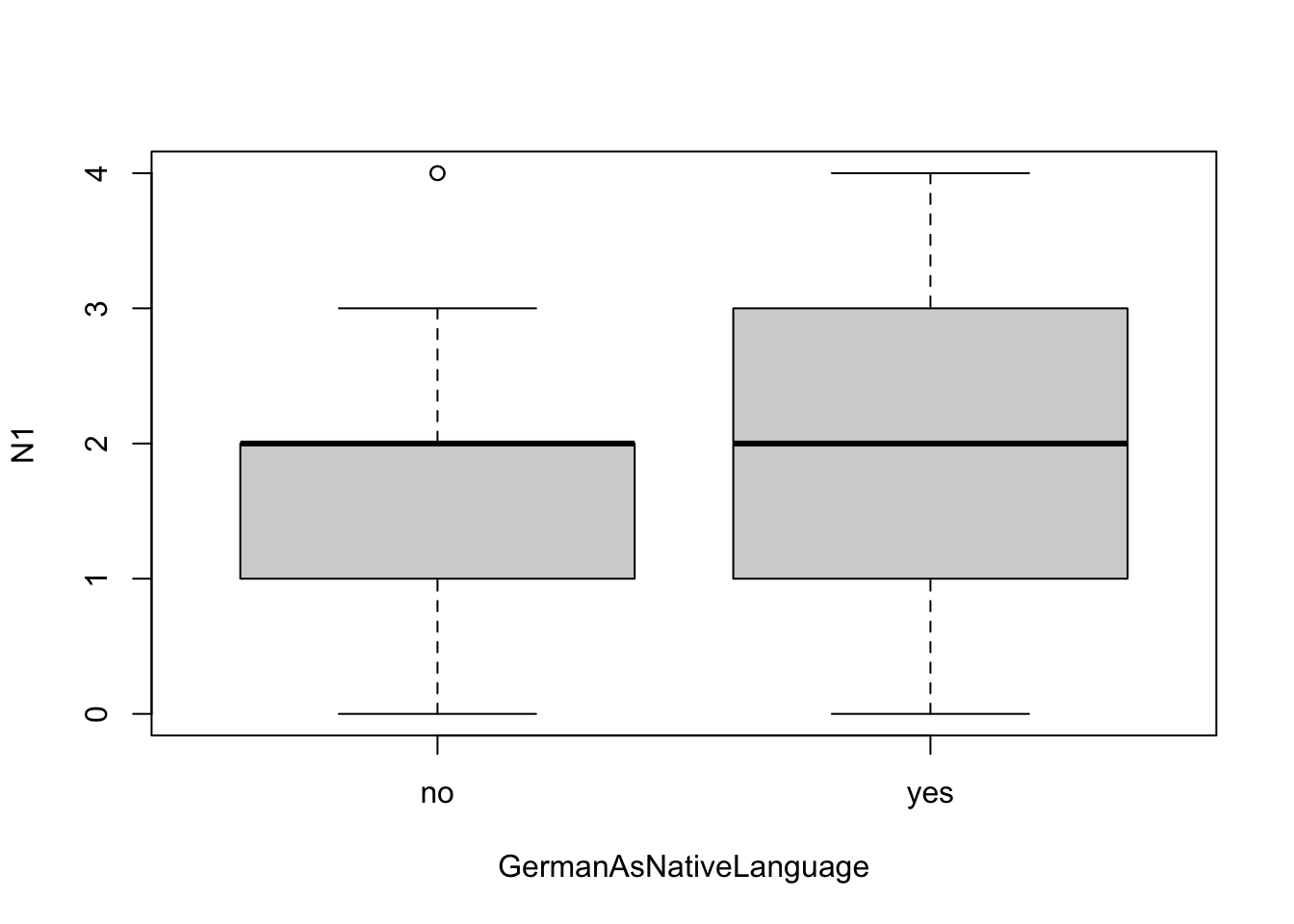
Vorsicht: bei
boxplot()sind Formel- und herkömmliche Schreibweise nicht austauschbar, wie oben im Beispiel beiplot(). Werden beide Variablen als einzelne Argumente angegeben, wird für beide Variablen ein einzelnes Boxplot gezeichnet. Für die diskrete VariableGermanAsNativLanguageist das keine sinnvolle Darstellung. Sind diskrete Variablen als Typfactorim data.frame, dann schlägt der Befehl in dieser Schreibweise ohnehin fehl.
Kombinierte Grafikbefehle
Grafisch können wir uns die bivariaten Zusammenhänge der Variablen mit Scatterplots und Histogrammen mit dem Befehl pairs.panels() aus dem Paket psych() - je nach Anzahl der Variablen mal mehr oder weniger übersichtlich - anzeigen lassen. Der Übersichtlichkeit halber begrenzen wir die Zahl der Variablen auf die ersten 5 (vars[1:5]), bevor wir den Datensatz grafisch veranschaulichen. Im Plot sehen wir
- in der Diagonalen die Histogramme jedes Items,
- unterhalb der Diagonalen Scatterplots der Items untereinander mit einem Linearen Fit (rot) und einer Ellipse (schwarz, schlecht lesbar) die die Stärke der Korrelation illustriert
- oberhalb der Diagonalen die bivariaten Korrelationen der Items untereinander.
pairs.panels(x = neo_dat[, vars[1:5]], # Auswahl des Datensatzes
lm = TRUE, # Einzeichnen einer gefitteten Regressionsgeraden
density = FALSE, # Keine Dichte in Histogrammen einzeichnen
jiggle = TRUE) # Die Punkte im Scatterplot zufällig streuen für bessere Übersicht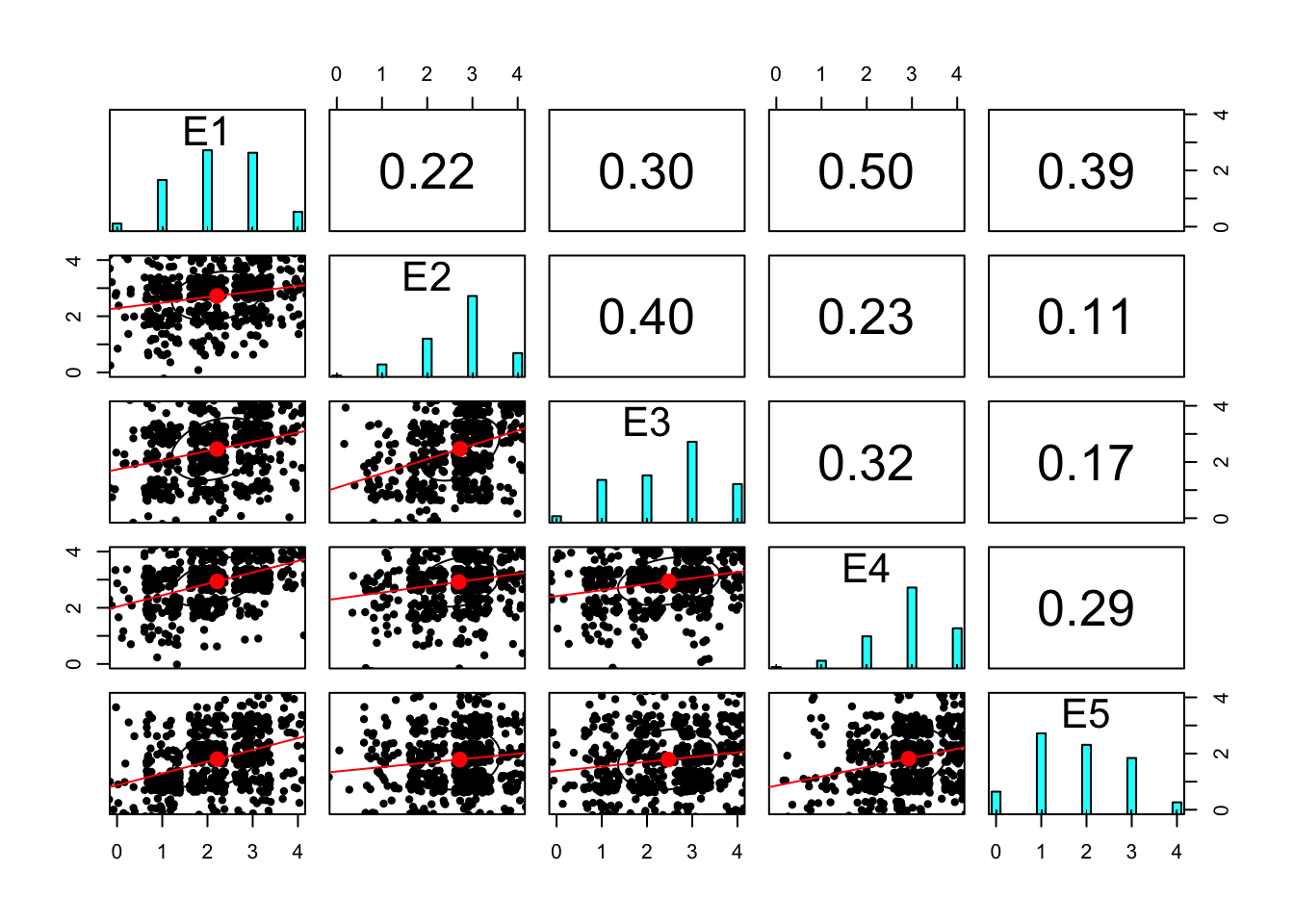
Alternative ggplot2
Alternativ können wir schöne plots wie Histogramme oder Streudiagramme auch mit dem Paket ggplot2 (Wickham 2016) erstellen. Dieses Paket erfordert jedoch eine etwas andere Syntax. Einzelne Ebenen der Grafik werden mit eigenen Befehlen erzeugt und mit einem + zu einer gemeinsamen Grafik zusammengefügt. Mit dem ersten Befehl ggplot() legen Sie die “Grundlage” des Plots, in dem Sie z.B. angeben, um welche Daten es sich in der Darstellung überhaupt handelt. Auf diese Grundlage setzen Sie dann mit geom_bar() ein Barplot der Variable E1:
library(ggplot2) ##ggf. vorher mit install.packages("ggplot2") installieren.
ggplot(data = neo_dat) + geom_bar(aes(E1)) # für andere Items statt 'E1' den jeweiligen anderen Namen angeben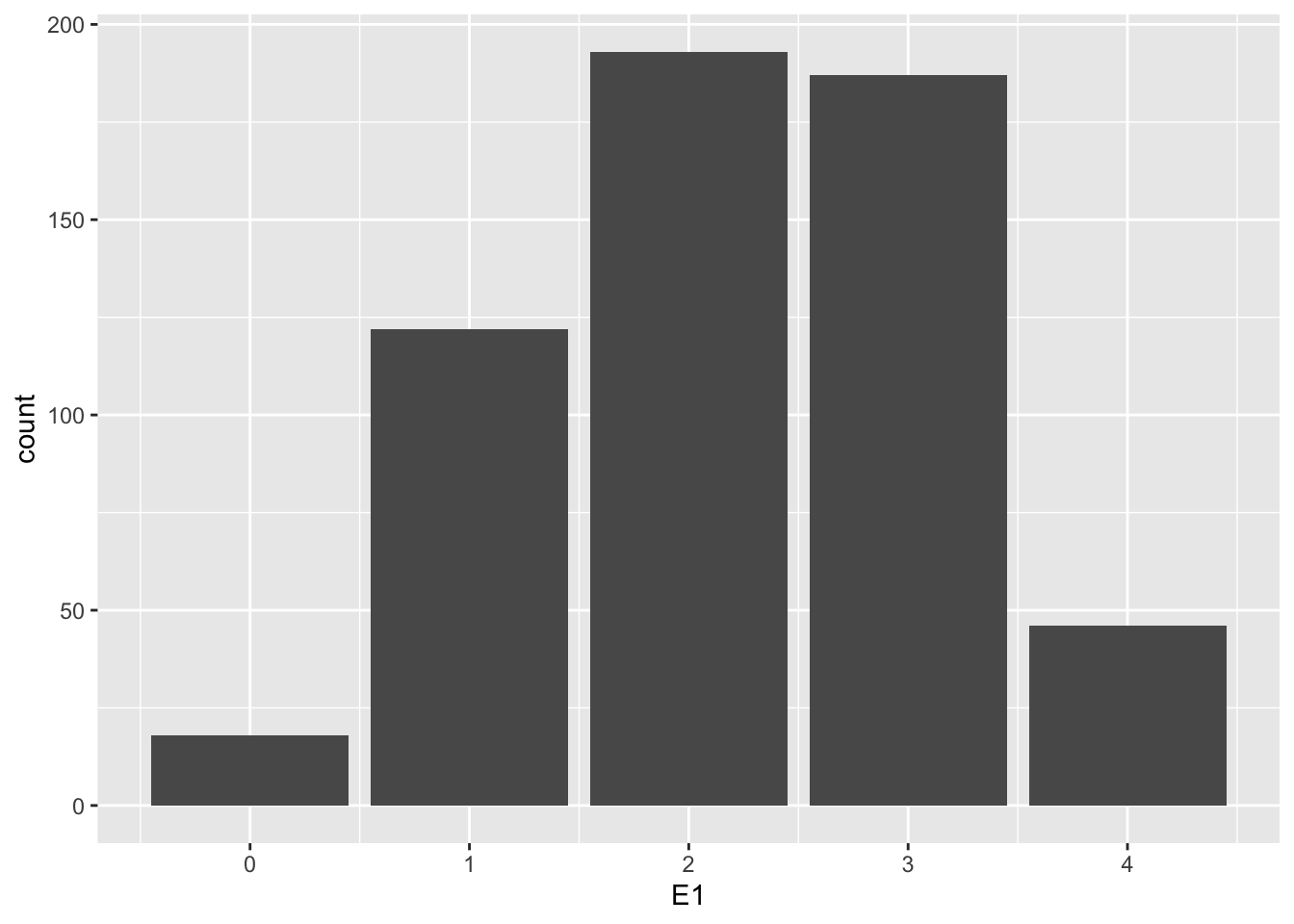
Auch ein Scatterplot kann mit Befehlen aus dem Paket ggplot2 schön dargestellt werden. Bei Daten - z.B. aus Fragebogenitems - die nur diskrete Werte annehmen können (Bsp. 0 - 4 als ganze Zahlen) empfiehlt es sich, die einzelnen Punkte zufällig etwas zu streuen (“jitter”). Zum Vergleich unten mal die beiden Varianten geom_point() links für die ungestreuten Daten und geom_jitter() rechts, für die gestreuten. Wichtig zu beachten ist, dass die gestreute Darstellung lediglich ein grafischer Trick ist, um deutlich zu machen, wie die Punkte verteilt sind. Vor dem Erstellen der Grafik wird für jeden Wert auf x- und y-Achse temporär ein zufälliger positiver oder negativer Wert addiert um jeden Punkt leicht gegenüber seinem eigentlichen Wert zu verschieben. An den Daten selbst wird dabei aber nichts verändert.
# Daten im Original:
ggplot(data = neo_dat) + geom_point(aes(x = E1, y = E2))
# Daten mit etwas zufälliger Streuung. Eine Häufung ist hier deutlicher sichtbar.
ggplot(data = neo_dat) + geom_jitter(aes(x = E1, y = E2)) 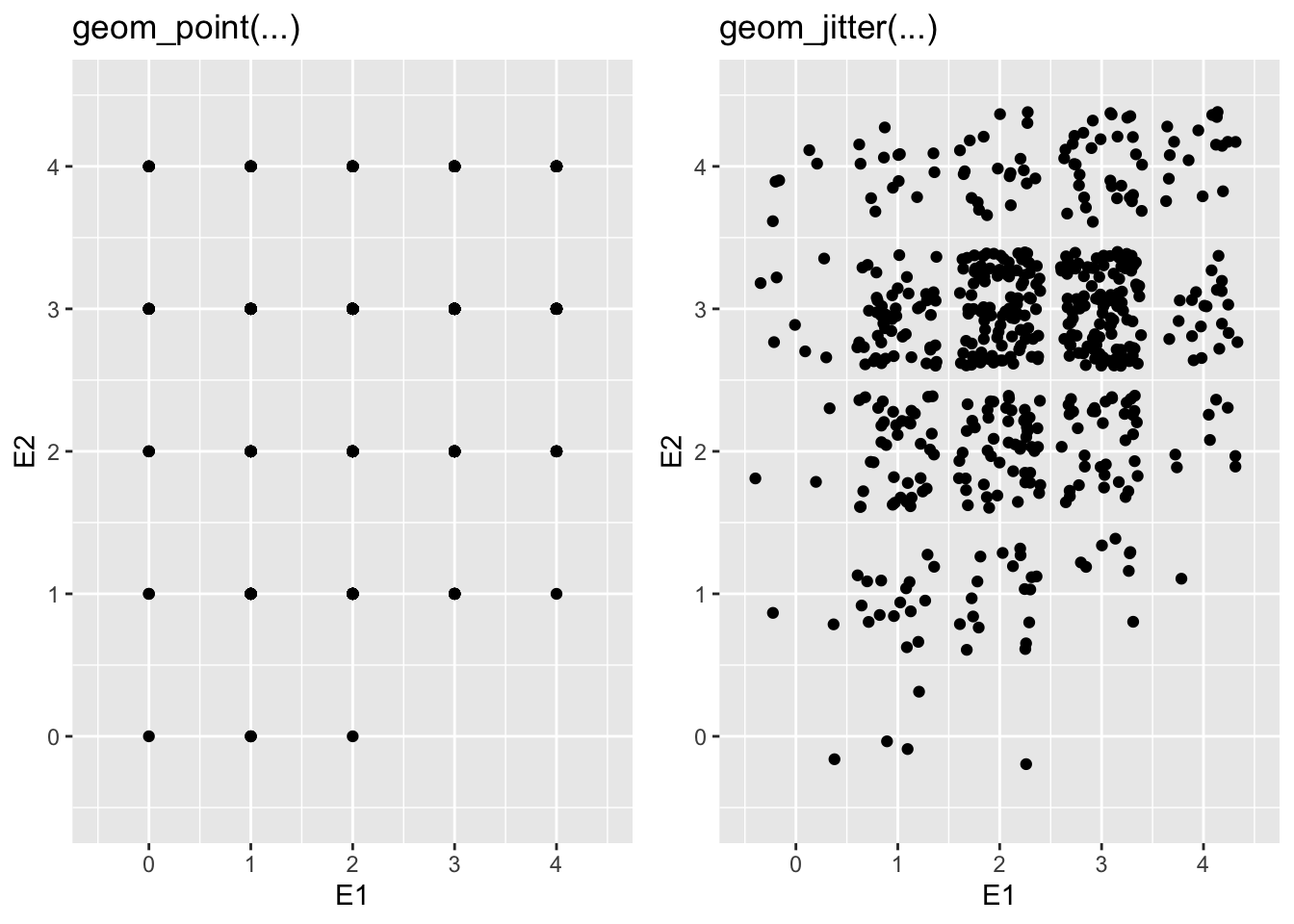
Literatur
Fußnoten
Natürlich müssen Sie dafür vorher installiert worden sein, wie im Tutorial Teil 1 beschrieben.↩︎
Die gedrehten Labels der x-Achse können über das zusätzliche Argument
barplot(..., las = 2)erstellt werden↩︎Wir müssen hier noch einmal den Befehl
table()dazwischen schieben, da wir ja kein Barplot der Daten (neo_dat$Age_cat), sondern der Häufigkeitstabelle der Datentable(neo_dat$Age_cat)erstellen möchten. Im oberen Fall stellt das ObjektHbereits die vorher erstellte Häufigkeitstabelle dar.↩︎Das liegt daran, dass in den meisten Fällen in der Statistik die deskriptiven Maße weniger wichtig sind als die Schätzungen der unbekannten Populationsstreuung. Die Funktionen zur Schätzung der Populationsvarianz und -standardabweichung sind
var()undsd().↩︎Um eine unbekannte Populationskovarianz aus Stichprobendaten zu schätzen, können Sie die Funktion
cov()verwenden.↩︎Bei Werten die von 1 - 5 kodiert sind, wäre die Operation \(6 - \text{Rohwert} = \text{Umkodierter Wert}\).↩︎
Ob und inwieweit diese Verrechnung der Items zulässig ist, lernen Sie im Modul Diagnostik 1.↩︎