Übungsblatt 02
DESKRIPTIVE STATISTIK 1: Häufigkeiten, Maßzahlen und graphische Darstellungen
- Erläutern Sie den Unterschied zwischen einem Messwert und einer Messwertausprägung.
Ein Messwert oder ein Variablenwert bezeichnet den Wert, den eine Person auf Basis einer Messung zugewiesen bekommt. Die unterschiedlichen Ausprägungen die diese Messwerte in der Beobachtung annehmen sind die Messwertausprägungen. Die Menge aller Messwertausprägungen bilden den Wertebereich der Messwerte. Da Tabellen der Ordnung und der Zusammenfassung von Daten dienen, werden dort i.A. die Messwertausprägungen (und nicht die Messwerte) in aufsteigender Reihenfolge aufgelistet. Durch die Angabe, wie oft jede Messwertausprägung beobachtet wurde (d.h. durch die Bestimmung von Häufigkeiten), liegt in einer Tabelle die Information über die Gesamtheit der Messwerte, d.h. der Daten vor.
Eine Mathematikklausur in der 9. Klasse hat folgende Urliste ergeben:
6, 6, 4, 2, 6, 3, 2, 2, 1, 2, 2, 6, 3, 3, 2, 3, 1, 1, 3, 1, 6, 2, 4, 4, 1Geben Sie die absoluten kumulierten Häufigkeiten an.
TippLösungNote H h h(%) Hkum hkum hkum(%) 1 5 0,20 20 5 0,20 20 2 7 0,28 28 12 0,48 48 3 5 0,20 20 17 0,68 68 4 3 0,12 12 20 0,80 80 6 5 0,20 20 25 1,00 100 Geben Sie die relativen kumulierten Häufigkeiten in Prozent an.
TippLösungNote H h h(%) Hkum hkum hkum(%) 1 5 0,20 20 5 0,20 20 2 7 0,28 28 12 0,48 48 3 5 0,20 20 17 0,68 68 4 3 0,12 12 20 0,80 80 6 5 0,20 20 25 1,00 100 Geben Sie den Messwert \(x_{4}\) bezogen auf die obige Datenreihe an.
TippLösung\(x_4 = 2\), da der vierte Wert der Urliste 2 ist.
\(H\left( x_{3} \right) = ?\)
TippLösung\(H\left( x_{3} \right) = 5\)
Bei \(x_{3}\) handelt es sich hier um die 3. Messwertausprägung der sortierten Urliste. Das lässt sich daraus schließen, dass nach einer (absoluten) Häufigkeit gefragt ist und Häufigkeiten nur für Messwertausprägungen eine sinnvolle Information darstellen.
Berechnen Sie Mittelwert, Median, Modus und Standardabweichung.
TippLösungMittelwert:
\(\bar{x} = \frac{1}{n}\sum_{i=1}^n x_i = \frac{1}{25}(6 + 6 + 4 + 2 + ... + 4 + 1)= 3.04\)
Median:
Da \(n\) ungerade (\(n = 25\)) gilt:
\(Md = x_{(\frac{n + 1}{2})} = x_{(\frac{25 + 1}{2})} = x_{(13)} = 3\)
Geordnete Urliste: 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 6, 6, 6, 6, 6
An diesem Datenbeispiel kann man übrigens sehen, warum die Interpretation des Medians ist, dass mindestens 50 % der Beobachtungen kleiner oder gleich dem Median sind. Laut Berechnungsvorschrift ist der Median \(Md = 3\). Tatsächlich weisen 17 der 25 Beobachtungen einen Wert von 3 oder kleiner auf, was einem Anteil von 68 % entspricht.
Modus:
\(Mod = 2\)
da die Messwertausprägung \(x_2 = 2\) der Wert mit der maximalen absoluten Häufigkeit \(H(2) = 7\) ist.
Standardabweichung:
\[\begin{align*} s_{emp} &= \sqrt{\frac{1}{n}\sum_{i = 1}^n(x_i - \bar{x})^2} \\ &= \sqrt{\frac{1}{n}[(x_1 - \bar{x})^2 + (x_2 - \bar{x})^2 + (x_3 - \bar{x})^2 + ... + (x_{24} - \bar{x})^2 + (x_{25} - \bar{x})^2]} \\ &= \sqrt{\frac{1}{25}[(6 - 3.04)^2 + (6 - 3.04)^2 + (4 - 3.04)^2 + ... + (4 - 3.04)^2 + (1 - 3.04)^2]} \\ \\ &\approx 1.73 \end{align*}\]
Berechnen Sie für die Messwerte aus der Aufgabe 2:
\(\sum_{i = 1}^{3}x_{i}\)
TippLösung\(\sum_{i = 1}^{3}x_{i}\) bedeutet, dass die Werte 1 bis 3 der Urliste aufsummiert werden. Also
\(\sum_{i = 1}^{3}x_{i} = x_1 + x_2 + x_3 = 6 + 6 + 4 = 16\)
\(\sum_{i = 1}^{5}{{(x}_{i} - 1)}\)
TippLösung\[\begin{align*} \sum_{i = 1}^{5}{{(x}_{i} - 1)} &= (x_1 - 1) + (x_2 - 1) + (x_3 - 1) + (x_4 - 1) + (x_5 - 1) \\ &= (6 - 1) + (6 - 1) + (4 - 1) + (2 - 1) + (6 - 1) \\ &= 5 + 5 + 3 + 1 + 5 \\ &= 19 \end{align*}\]
Hier wird bei jedem Summanden \(x_{i}\) einzeln der Wert 1 abgezogen und dann alle Werte addiert.
\(\sum_{i = 1}^{3}{x_{i} - 1}\)
TippLösung\[\begin{align*} \sum_{i = 1}^{3}{x_{i} - 1} &= (x_1 + x_2 + x_3) - 1 \\ &= (6 + 6 + 4) - 1 \\ &= 16 - 1 \\ &= 15 \end{align*}\]
Hier wird zunächst die Summe der ersten 3 Werte der Liste berechnet, und anschließend wird von dieser gesamten Summe 1 subtrahiert.
\(\sum_{i = 2}^{4}{(x_{i} - 1)}^{2}\)
TippLösung\[\begin{align*} \sum_{i = 2}^{4}{(x_{i} - 1)}^{2} &= (x_2 - 1) ^2 + (x_3 - 1)^2 + (x_4 - 1)^2 \\ &= {(6 - 1)}^{2} + {(4 - 1)}^{2} + {(2 - 1)}^{2} \\ &= 5^{2} + 3^{2} + 1^{2} \\ &= 25 + 9 + 1 \\ &= 35 \end{align*}\]
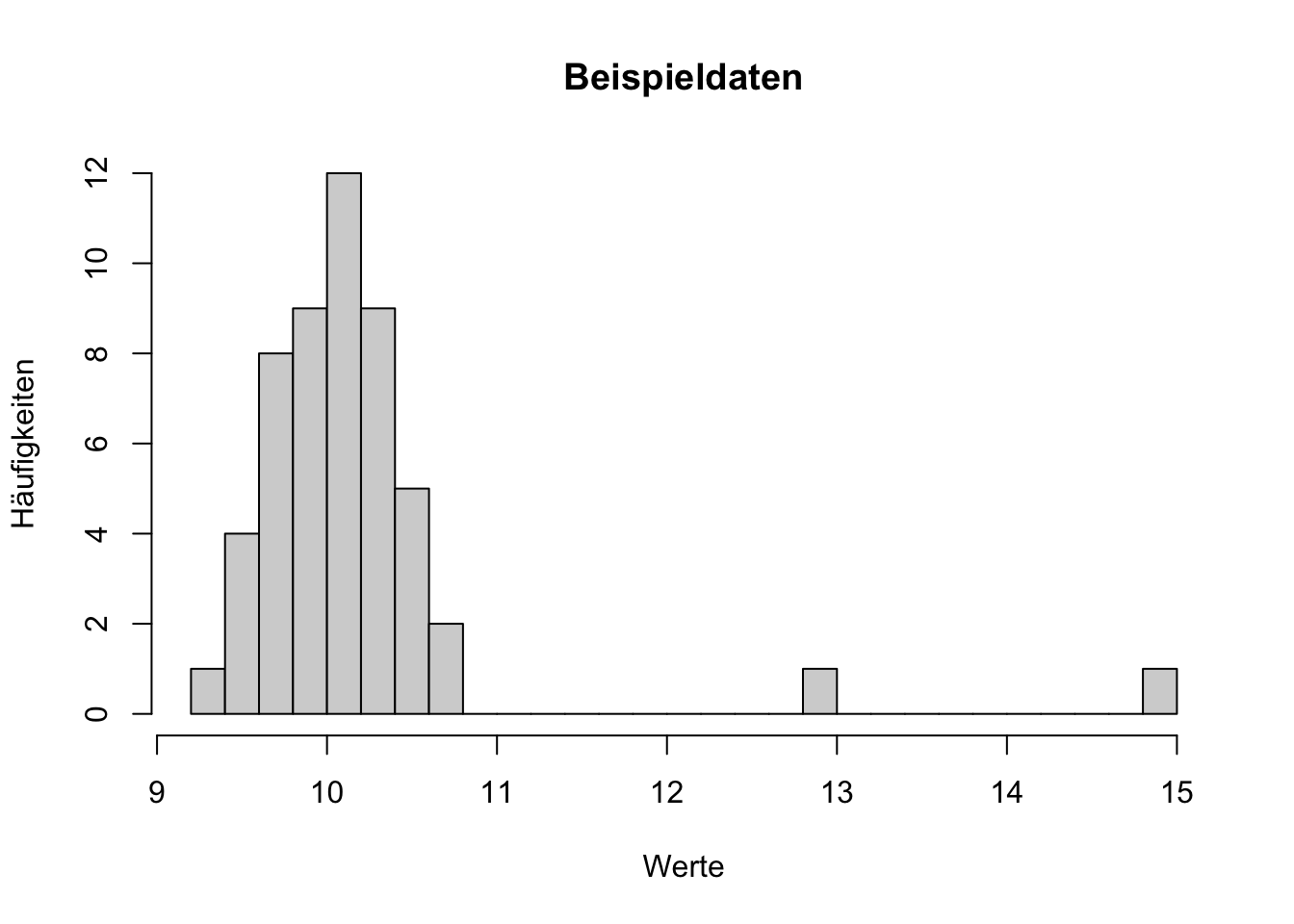
Welche Maße der zentralen Tendenz bieten sich zur Beschreibung der unten dargestellten Variablen besonders an? Begründen Sie.
Histogramm einer Variable TippLösungEs liegen zwei Ausreißer vor, die deutlich größer sind als der Rest der Messwerte. Deshalb sind Maße, die wenig ausreißersensitiv sind, besser zur Beschreibung geeignet. Dies trifft auf die Maße Modalwert und Median zu. Der Mittelwert ist hingegen weniger gut geeignet, da er ausreißersensitiv ist.
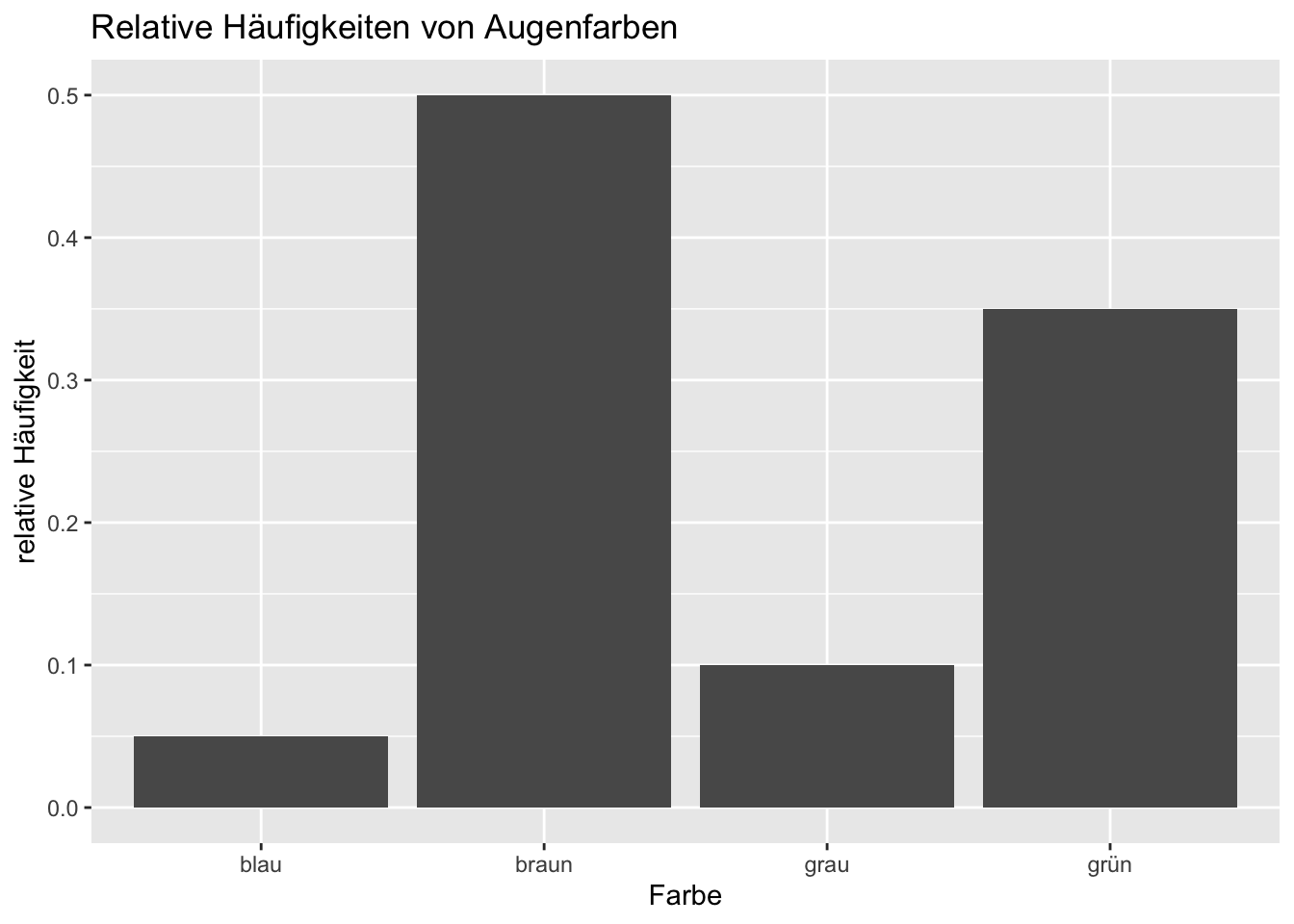
Säulendiagramm mit relativen Häufigkeiten von Augenfarben. TippLösungModus, da hier eine diskrete kategoriale Variable dargestellt ist.
Ihnen liegen die folgenden Quantile vor:
0% 5% 10% 15% 20% 25% 30% 35% 40% 45% 50% 55% 60% -2.50 1.62 3.12 4.56 6.50 7.58 8.23 8.61 9.17 9.96 10.35 11.24 12.31 65% 70% 75% 80% 85% 90% 95% 100% 13.05 13.70 14.41 15.50 15.93 17.39 20.05 25.36Minimaler und maximaler Messwert sind hierbei:
\(x_{\min} = -2.5\) und \(x_{\max} = 25.36\)
Skizzieren Sie einen Boxplot, basierend auf den in der Tabelle angegebenen Quantilen. Hinweis: Ausreißer müssen Sie in Ihrem Plot nicht berücksichtigen.
TippLösung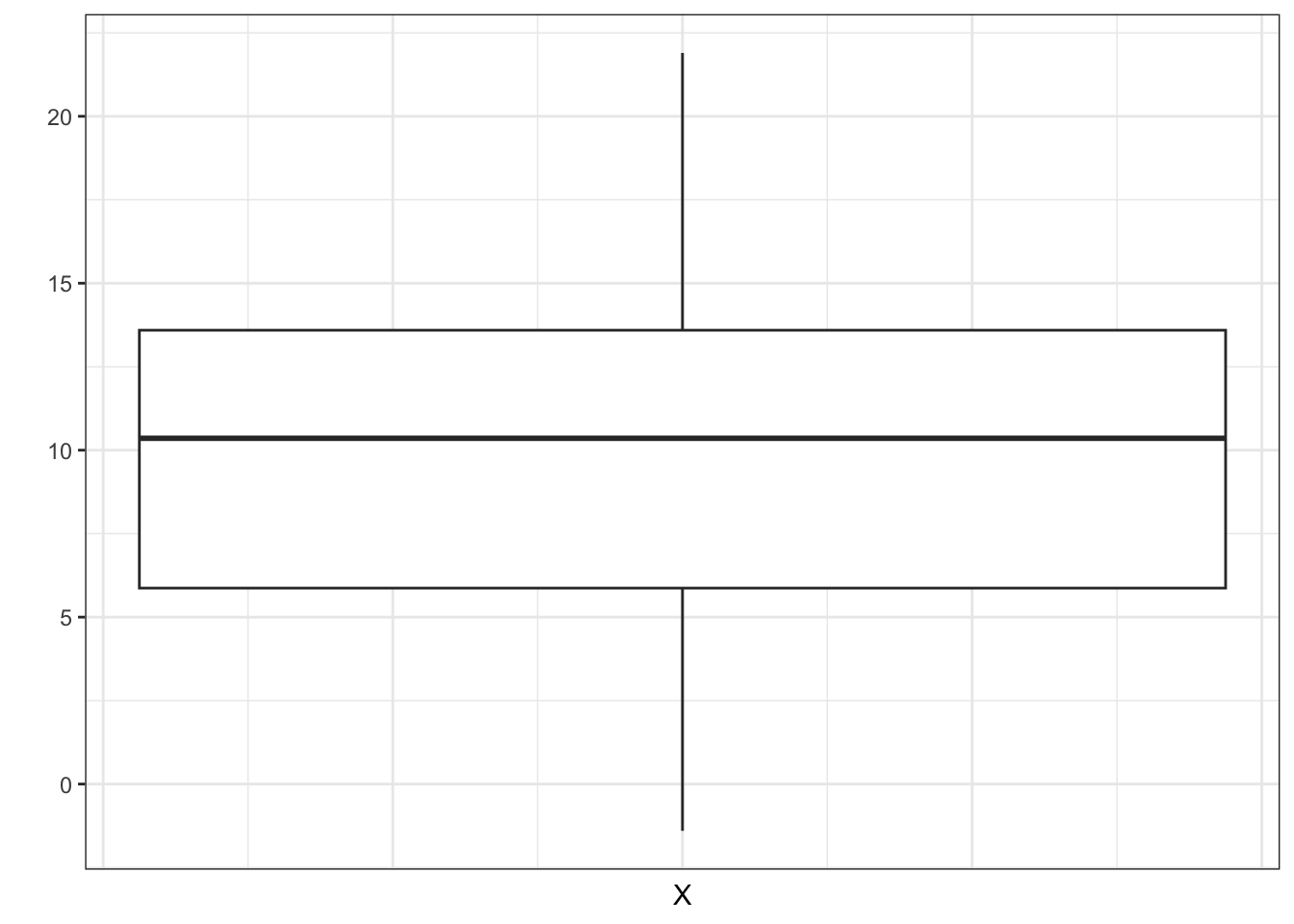
Boxplot
Laden Sie den Datensatz herunter und speichern Sie ihn auf Ihrem Computer ab. Lesen Sie den Datensatz dann wie im Einführungsvideo gezeigt mit dem Befehl
read.csv2( ... )ein und weisen Sie ihn einem Objekt mit dem Namen Daten zu. (Hinweis: Vergessen Sie nicht die notwendigen Schritte zum Einlesen von Daten, die im Tutorial Teil 2 beschrieben sind.)Im Datensatz sind von sieben Personen das Studienfach, das Alter, das Bundesland aus dem sie kommen, ihre Abiturnote und ihre Anreisezeit in Minuten (Anreise_min) erfasst.
TippLösung## Daten einlesen Daten <- read.csv2('Beispieldaten.csv')Berechnen Sie in R für jede Person die Anreisezeit in Sekunden. Fügen Sie das Ergebnis der Tabelle Daten als neue Spalte „Anreise_sec” hinzu. Hinweis: Zuweisungen zu neuen Spalten können Sie mit Hilfe von
$und<-machen. Also z.B. mit einer Zuweisung mitDaten$Anreise_sec <- ...TippLösung## Anreisezeit in Sekunden umrechnen und zu Datensatz hinzufügen Daten$Anreise_sec <- Daten$Anreise_min * 60Erstellen Sie mit der Funktion
table()eine Häufigkeitstabelle, die jeder Ausprägung der Spalte Alter des Objekts Daten eine absolute Häufigkeit zuweist. Speichern Sie das Ergebnis als Objekt H ab.TippLösung## Absolute Häufigkeiten: H <- table(Daten$Alter) H21 24 28 31 2 1 2 1Erstellen Sie eine Häufigkeitstabelle, die jeder Altersausprägung eine relative Häufigkeit zuweist. Wandeln Sie hierfür die absoluten Häufigkeiten aus H mithilfe der Funktion
prop.table()in relative Häufigkeiten um. Speichern Sie das Ergebnis als Objekt h ab.TippLösung## Relative Häufigkeiten h <- prop.table(H) h21 24 28 31 0.3333333 0.1666667 0.3333333 0.1666667Erstellen Sie eine Häufigkeitstabelle, die jeder Altersausprägung eine absolute kumulierte Häufigkeit zuweist. Wandeln Sie hierfür die absoluten Häufigkeiten aus H mithilfe der Funktion
cumsum()in absolute kumulierte Häufigkeiten um. Speichern Sie das Ergebnis als Objekt Hkum ab.TippLösung## Absolute kumulierte Häufigkeiten: Hkum <- cumsum(H) Hkum21 24 28 31 2 3 5 6Erstellen Sie eine Häufigkeitstabelle, die jeder Altersausprägung eine relative kumulierte Häufigkeit zuweist. Wandeln Sie hierfür die relativen Häufigkeiten aus h mithilfe der Funktion
cumsum()in relative kumulierte Häufigkeiten um. Speichern Sie das Ergebnis als Objekt hkum ab.TippLösung## Relative kumulierte Häufigkeiten hkum <- cumsum(h) hkum21 24 28 31 0.3333333 0.5000000 0.8333333 1.0000000Erstellen Sie mit der Funktion
barplot()jeweils ein Balkendiagramm für H, h, Hkum, hkum!TippLösung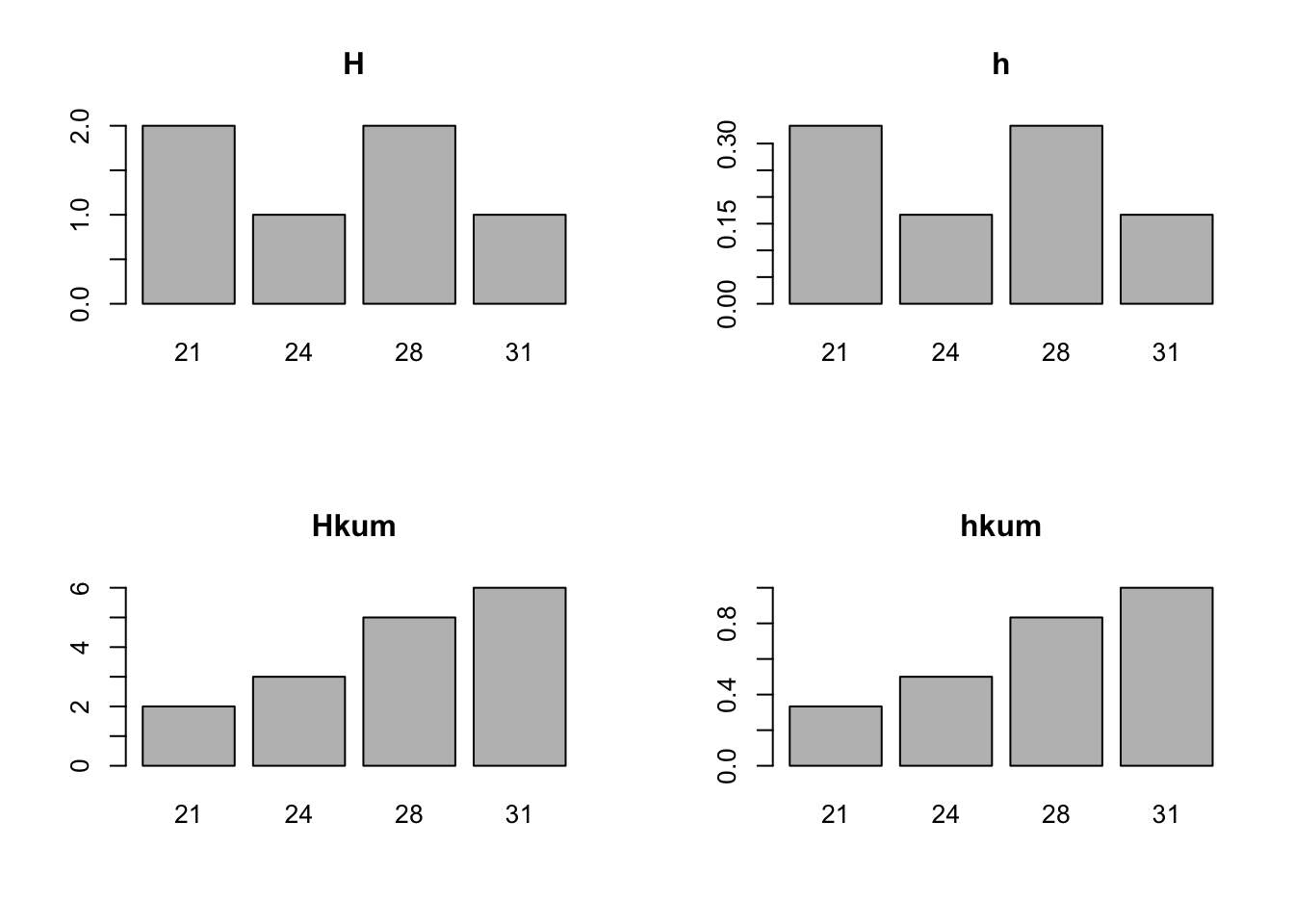
## Balkendiagramme barplot(H) barplot(h) barplot(Hkum) barplot(hkum)Erstellen Sie für die Variable Anreisezeit_in_Sekunden mit der Funktion
hist()ein Histogramm. Warum eignet sich für diese Variable als graphische Darstellung ein Histogramm?TippLösung## Histogramm Anreisezeit hist(Daten$Anreise_sec)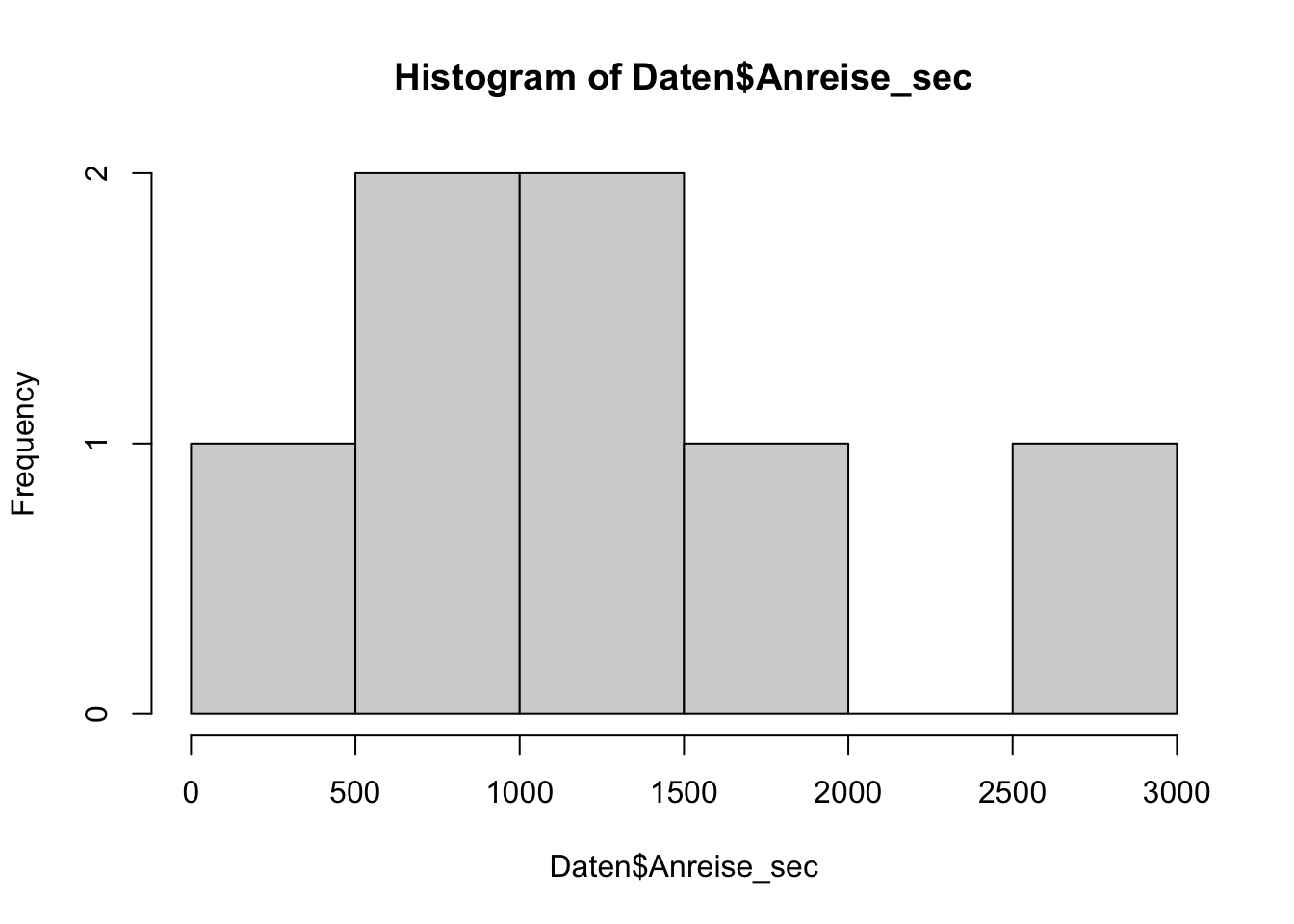
Ein Histogramm eignet sich besonders für stetige Variablen.
Berechnen Sie mithilfe von R die durchschnittliche Anreisezeit in Sekunden. Verwenden Sie hierfür die Funktion
mean().TippLösungmean(Daten$Anreise_sec)[1] 1345.714Wählen Sie nur die Versuchsteilnehmer aus, die Psychologie studieren und berechnen Sie für die Variable „Alter” den Mittelwert, und den Median. Verwenden Sie die Funktionen
mean()undmedian().Hinweis: Die Variable Alter enthält einen fehlenden Wert (
NA= not available). Welches Argument muss jeweils in die Funktion eingefügt werden, um Mittelwert und Median berechnen zu können?TippLösung## Datensatz nur mit Psychologiestudierenden Daten_Psy <- Daten[Daten$Studienfach == 'Psychologie', ] ## Mittelwert, Median und Standardabweichung berechnen. Das Argument ## na.rm = TRUE sorgt dafuer, dass fehlende Werte vor der Berechnung ## aus dem Vektor entfernt werden. mean(Daten_Psy$Alter) ## gibt NA aus, da Grundeinstellung na.rm = FALSE ist.[1] NAmean(Daten_Psy$Alter, na.rm = TRUE)[1] 22.5median(Daten_Psy$Alter, na.rm = TRUE)[1] 22.5