Übungsaufgaben
Weitere Verfahren im ein- und zweifaktoriellen varianzanalytischen Modell
Die hier veröffentlichten Übungsaufgaben sind brandneu und deshalb noch nicht auf Herz und Nieren überprüft. Sollten Sie Fehler entdecken, geben Sie uns bitte unbedingt eine Rückmeldung an philipp.sckopke(at)psy.lmu.de, damit wir so bald wie möglich eine verbesserte Version online stellen können.
Sie untersuchen, ob der Einfluss der zweistufigen Variable Risikobereitschaft (hoch vs. niedrig) auf die (stetige) Variable Neurotizismus vom Studienfach (Psychologie vs. BWL) abhängt. Die Ergebnisse zeigen keinen Interaktionseffekt, keinen Haupteffekt Risikobereitschaft und keinen Haupteffekt Studienfach. Zeichnen Sie in das nachfolgende Profildiagramm die Profillinien so ein, dass diese mit dem Ergebnis der Untersuchung nicht im Widerspruch stehen (Hinweis: möglicherweise gibt es mehr als eine richtige Lösung). Beschriften Sie dabei die x-Achse und die Profillinien und zeichnen Sie auch die Erwartungswerte \(\mu_{j \cdot}\) und \(\mu_{\cdot k}\) ein.
TippLösung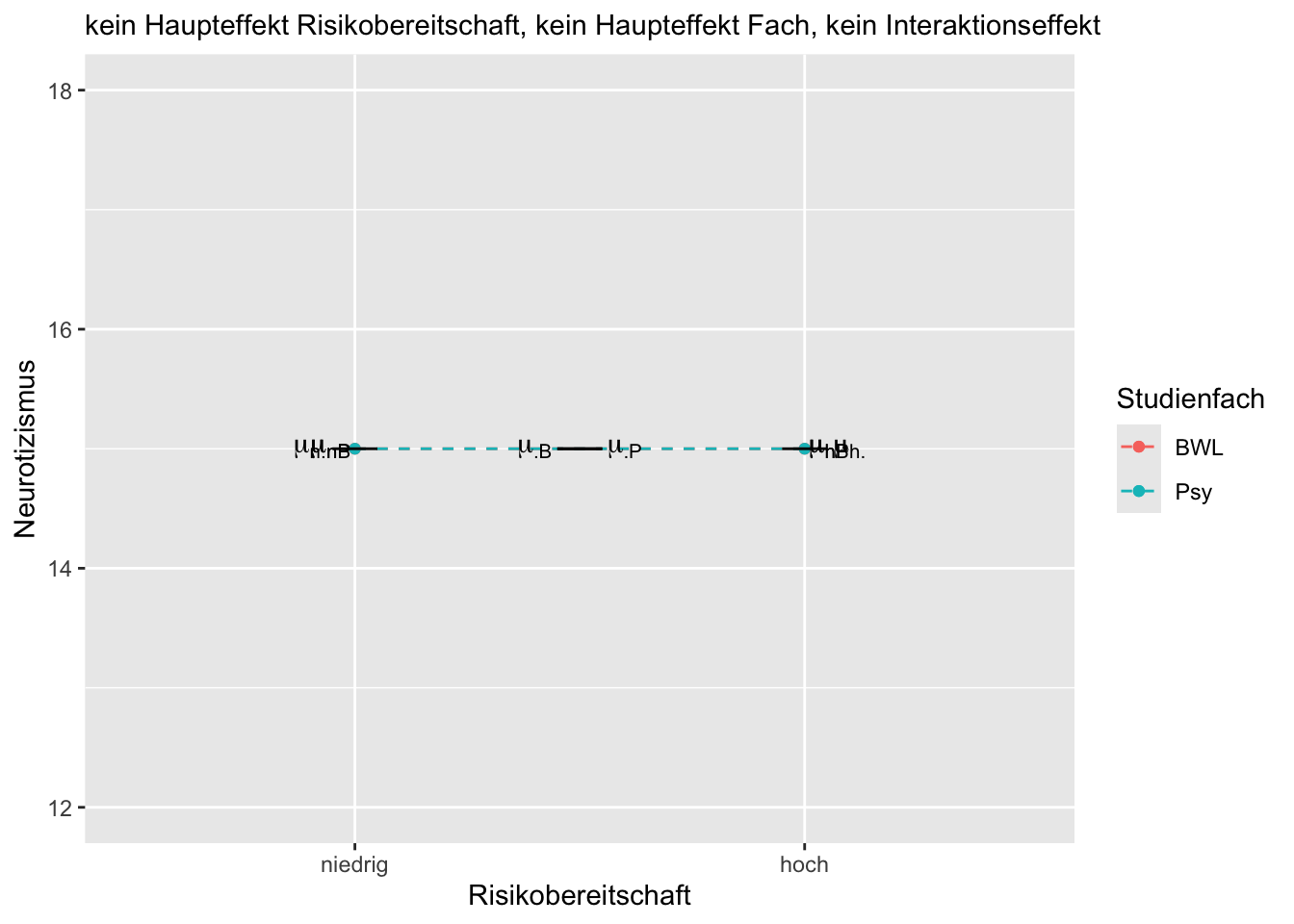
Erläuterung des oben gezeigten Beispiels:
Bei dem eingezeichneten Profilplot liegt keine Interaktion von Risikobereitschaft und Studienfach vor, da \(\mu_{nP} - \mu_{hP} = \mu_{nB} - \mu_{hB}\) bzw. \(\mu_{nP} - \mu_{nB}= \mu_{hP} - \mu_{hB}\). Es liegt kein Haupteffekt Studienfach vor, da \(\mu_{\cdot P} = \mu_{\cdot B}\). Es liegt kein Haupteffekt Risikobereitschaft vor, da \(\mu_{n \cdot} = \mu_{h \cdot}\).
Sie untersuchen, ob der Einfluss der zweistufigen Variable Risikobereitschaft (hoch vs. niedrig) auf die (stetige) Variable Neurotizismus vom Studienfach (Psychologie vs. BWL) abhängt. Die Ergebnisse zeigen keinen Interaktionseffekt, einen Haupteffekt Risikobereitschaft und einen Haupteffekt Studienfach. Zeichnen Sie in das nachfolgende Profildiagramm die Profillinien so ein, dass diese mit dem Ergebnis der Untersuchung nicht im Widerspruch stehen (Hinweis: möglicherweise gibt es mehr als eine richtige Lösung). Beschriften Sie dabei die x-Achse und die Profillinien und zeichnen Sie auch die Erwartungswerte \(\mu_{j \cdot}\) und \(\mu_{\cdot k}\) ein.
 TippLösung
TippLösung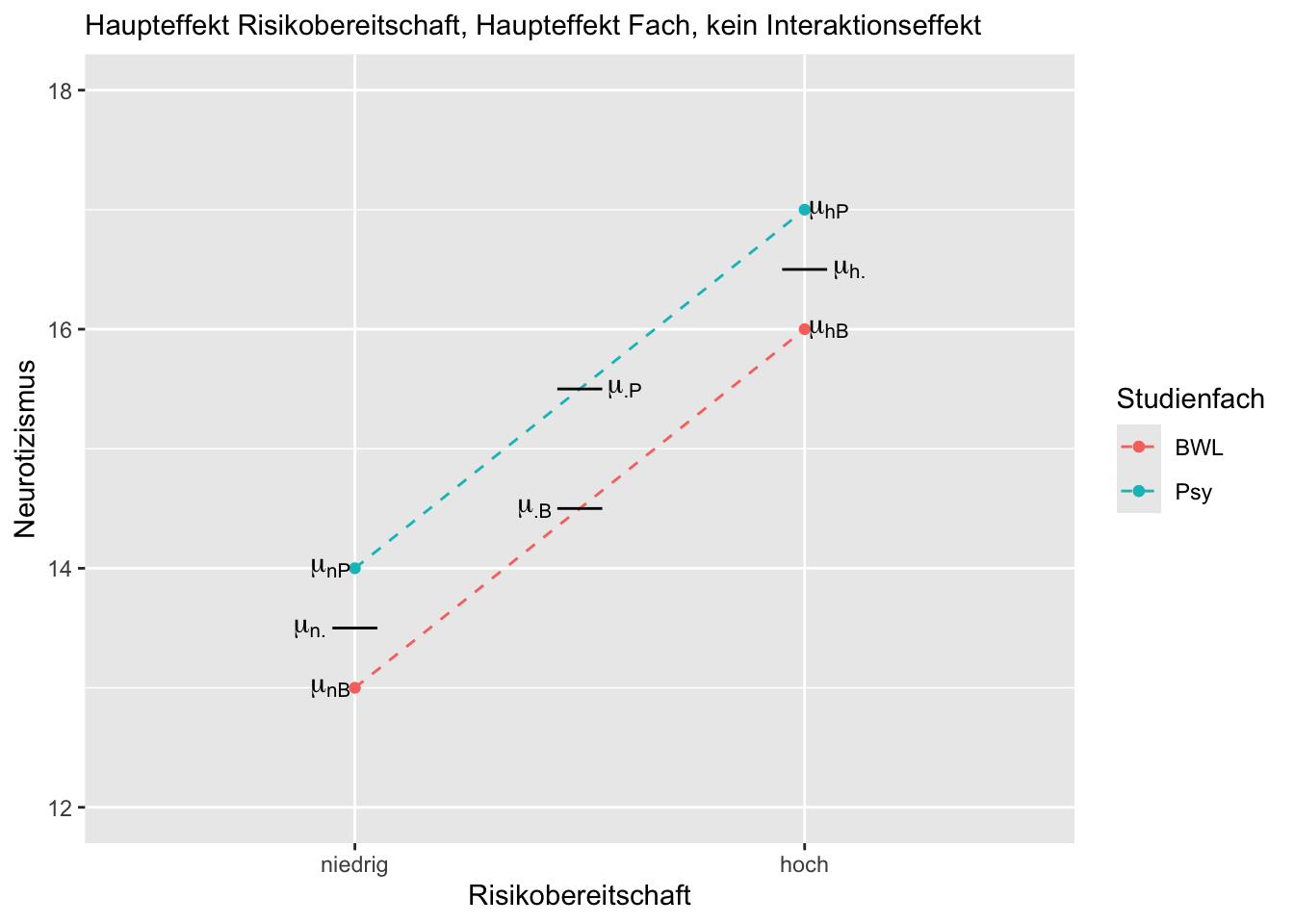
Erläuterung des oben gezeigten Beispiels:
Bei dem eingezeichneten Profilplot liegt keine Interaktion von Risikobereitschaft und Studienfach vor, da \(\mu_{nP} - \mu_{hP} = \mu_{nB} - \mu_{hB}\) bzw. \(\mu_{nP} - \mu_{nB}= \mu_{hP} - \mu_{hB}\). Es liegt ein Haupteffekt Studienfach vor, da \(\mu_{\cdot P} \neq \mu_{\cdot B}\). Es liegt ein Haupteffekt Risikobereitschaft vor, da \(\mu_{n \cdot} \neq \mu_{h \cdot}\).
Wichtig: Das ist natürlich nicht die einzige Möglichkeit eines Profilplots mit den gegebenen Anforderungen.
Sie untersuchen, ob der Einfluss der zweistufigen Variable Risikobereitschaft (hoch vs. niedrig) auf die (stetige) Variable Neurotizismus vom Studienfach (Psychologie vs. BWL) abhängt. Die Ergebnisse zeigen einen Interaktionseffekt, keinen Haupteffekt Risikobereitschaft und keinen Haupteffekt Studienfach. Zeichnen Sie in das nachfolgende Profildiagramm die Profillinien so ein, dass diese mit dem Ergebnis der Untersuchung nicht im Widerspruch stehen (Hinweis: möglicherweise gibt es mehr als eine richtige Lösung). Beschriften Sie dabei die x-Achse und die Profillinien und zeichnen Sie auch die Erwartungswerte \(\mu_{j \cdot}\) und \(\mu_{\cdot k}\) ein.
 TippLösung
TippLösung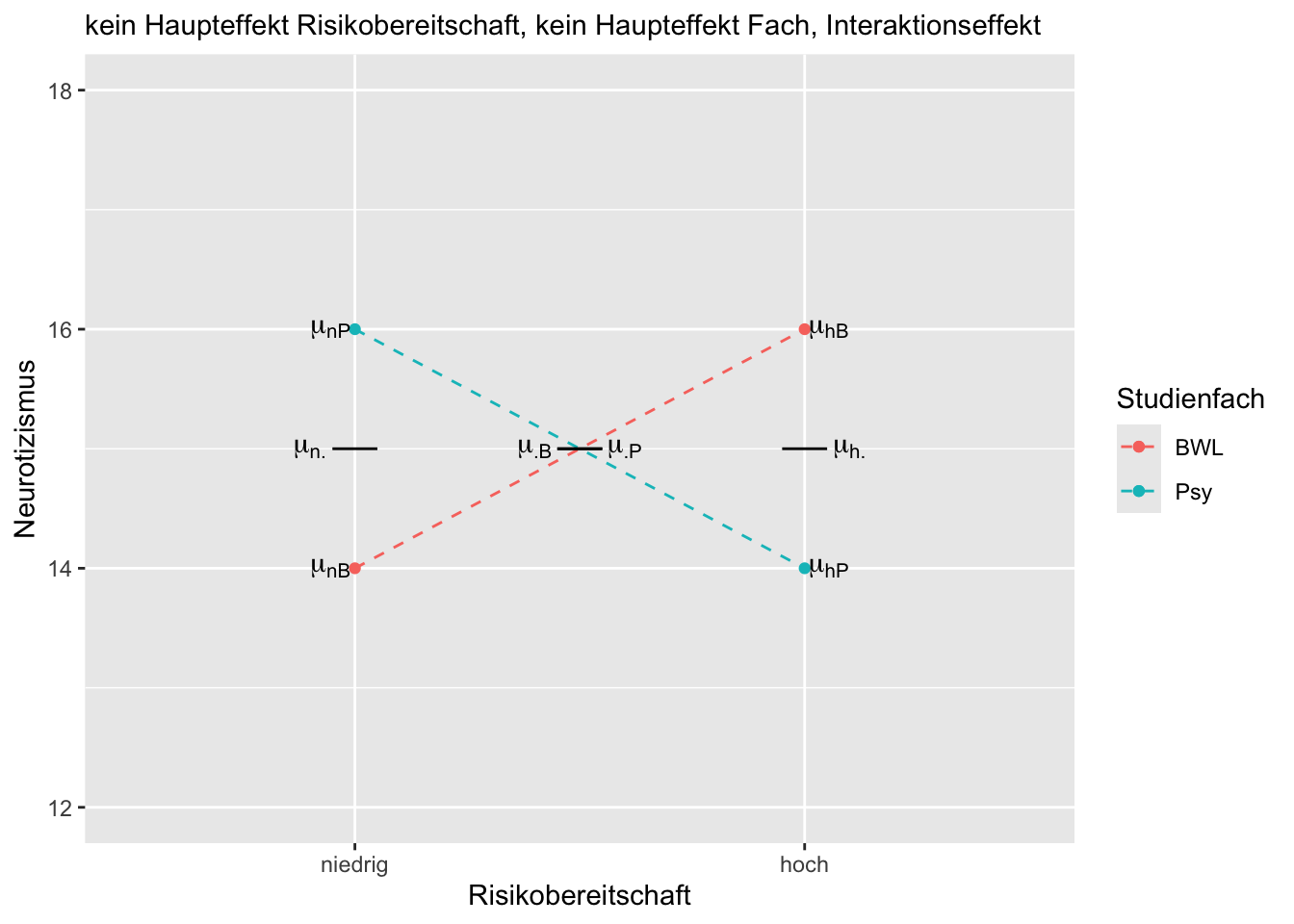
Erläuterung des oben gezeigten Beispiels:
Bei dem eingezeichneten Profilplot liegt eine Interaktion von Risikobereitschaft und Studienfach vor, da \(\mu_{nP} - \mu_{hP} \neq \mu_{nB} - \mu_{hB}\) bzw. \(\mu_{nP} - \mu_{nB}\neq \mu_{hP} - \mu_{hB}\). Es liegt kein Haupteffekt Studienfach vor, da \(\mu_{\cdot P} = \mu_{\cdot B}\). Es liegt kein Haupteffekt Risikobereitschaft vor, da \(\mu_{n \cdot} = \mu_{h \cdot}\).
Wichtig: Das ist natürlich nicht die einzige Möglichkeit eines Profilplots mit den gegebenen Anforderungen.
Sie untersuchen, ob der Einfluss der zweistufigen Variable Risikobereitschaft (hoch vs. niedrig) auf die (stetige) Variable Neurotizismus vom Studienfach (Psychologie vs. BWL) abhängt. Die Ergebnisse zeigen einen Interaktionseffekt, keinen Haupteffekt Risikobereitschaft und einen Haupteffekt Studienfach. Zeichnen Sie in das nachfolgende Profildiagramm die Profillinien so ein, dass diese mit dem Ergebnis der Untersuchung nicht im Widerspruch stehen (Hinweis: möglicherweise gibt es mehr als eine richtige Lösung). Beschriften Sie dabei die x-Achse und die Profillinien und zeichnen Sie auch die Erwartungswerte \(\mu_{j \cdot}\) und \(\mu_{\cdot k}\) ein.
 TippLösung
TippLösung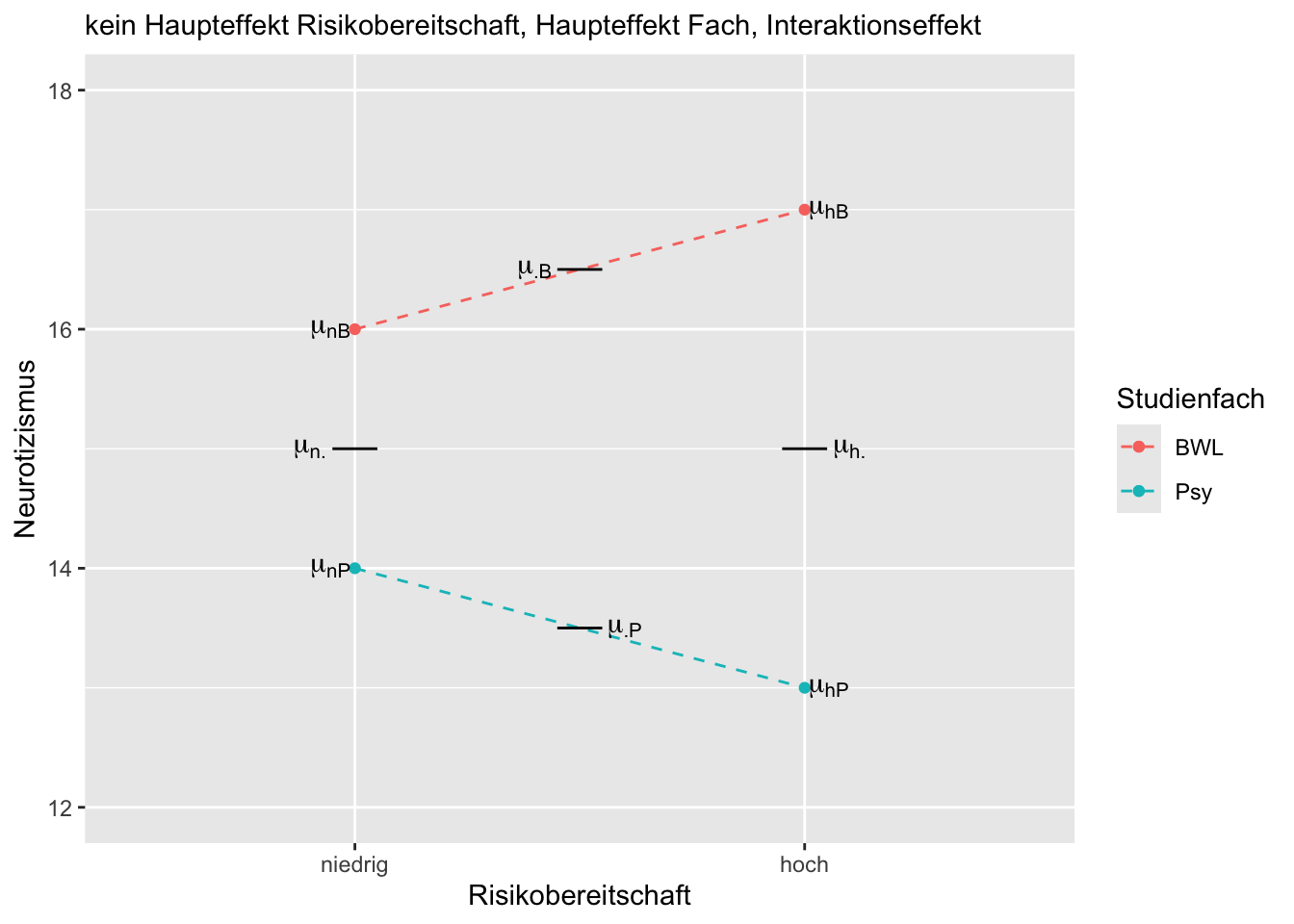
Erläuterung des oben gezeigten Beispiels:
Bei dem eingezeichneten Profilplot liegt eine Interaktion von Risikobereitschaft und Studienfach vor, da \(\mu_{nP} - \mu_{hP} \neq \mu_{nB} - \mu_{hB}\) bzw. \(\mu_{nP} - \mu_{nB}\neq \mu_{hP} - \mu_{hB}\). Es liegt ein Haupteffekt Studienfach vor, da \(\mu_{\cdot P} \neq \mu_{\cdot B}\). Es liegt kein Haupteffekt Risikobereitschaft vor, da \(\mu_{n \cdot} = \mu_{h \cdot}\).
Wichtig: Das ist natürlich nicht die einzige Möglichkeit eines Profilplots mit den gegebenen Anforderungen.
Sie untersuchen, ob der Einfluss der zweistufigen Variable Risikobereitschaft (hoch vs. niedrig) auf die (stetige) Variable Neurotizismus vom Studienfach (Psychologie vs. BWL) abhängt. Die Ergebnisse zeigen einen Interaktionseffekt, einen Haupteffekt Risikobereitschaft und keinen Haupteffekt Studienfach. Zeichnen Sie in das nachfolgende Profildiagramm die Profillinien so ein, dass diese mit dem Ergebnis der Untersuchung nicht im Widerspruch stehen (Hinweis: möglicherweise gibt es mehr als eine richtige Lösung). Beschriften Sie dabei die x-Achse und die Profillinien und zeichnen Sie auch die Erwartungswerte \(\mu_{j \cdot}\) und \(\mu_{\cdot k}\) ein.
 TippLösung
TippLösung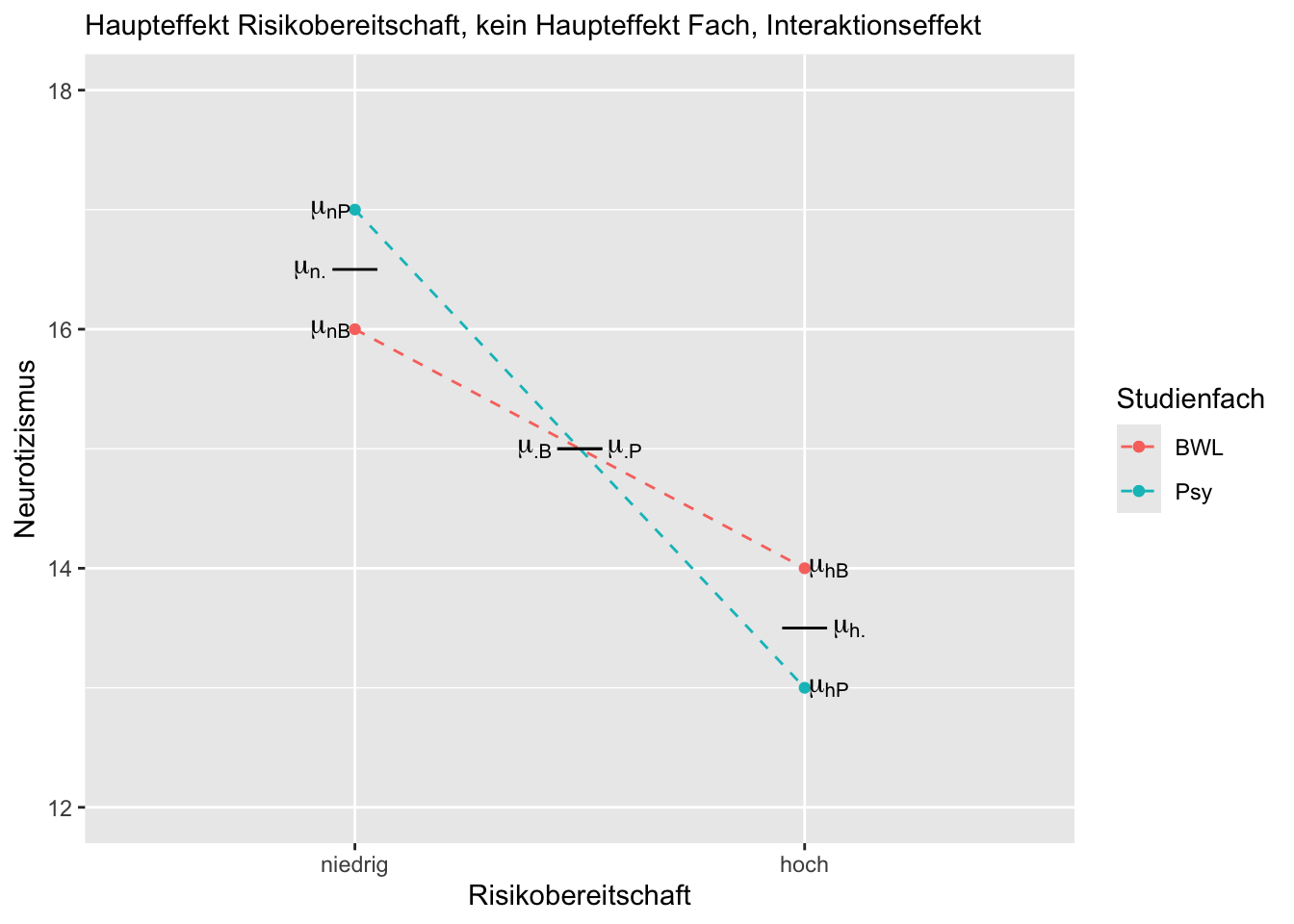
Erläuterung des oben gezeigten Beispiels:
Bei dem eingezeichneten Profilplot liegt eine Interaktion von Risikobereitschaft und Studienfach vor, da \(\mu_{nP} - \mu_{hP} \neq \mu_{nB} - \mu_{hB}\) bzw. \(\mu_{nP} - \mu_{nB}\neq \mu_{hP} - \mu_{hB}\). Es liegt kein Haupteffekt Studienfach vor, da \(\mu_{\cdot P} = \mu_{\cdot B}\). Es liegt ein Haupteffekt Risikobereitschaft vor, da \(\mu_{n \cdot} \neq \mu_{h \cdot}\).
Wichtig: Das ist natürlich nicht die einzige Möglichkeit eines Profilplots mit den gegebenen Anforderungen.
Sie untersuchen, ob der Einfluss der zweistufigen Variable Risikobereitschaft (hoch vs. niedrig) auf die (stetige) Variable Neurotizismus vom Studienfach (Psychologie vs. BWL) abhängt. Die Ergebnisse zeigen keinen Interaktionseffekt, keinen Haupteffekt Risikobereitschaft und einen Haupteffekt Studienfach. Zeichnen Sie in das nachfolgende Profildiagramm die Profillinien so ein, dass diese mit dem Ergebnis der Untersuchung nicht im Widerspruch stehen (Hinweis: möglicherweise gibt es mehr als eine richtige Lösung). Beschriften Sie dabei die x-Achse und die Profillinien und zeichnen Sie auch die Erwartungswerte \(\mu_{j \cdot}\) und \(\mu_{\cdot k}\) ein.
 TippLösung
TippLösung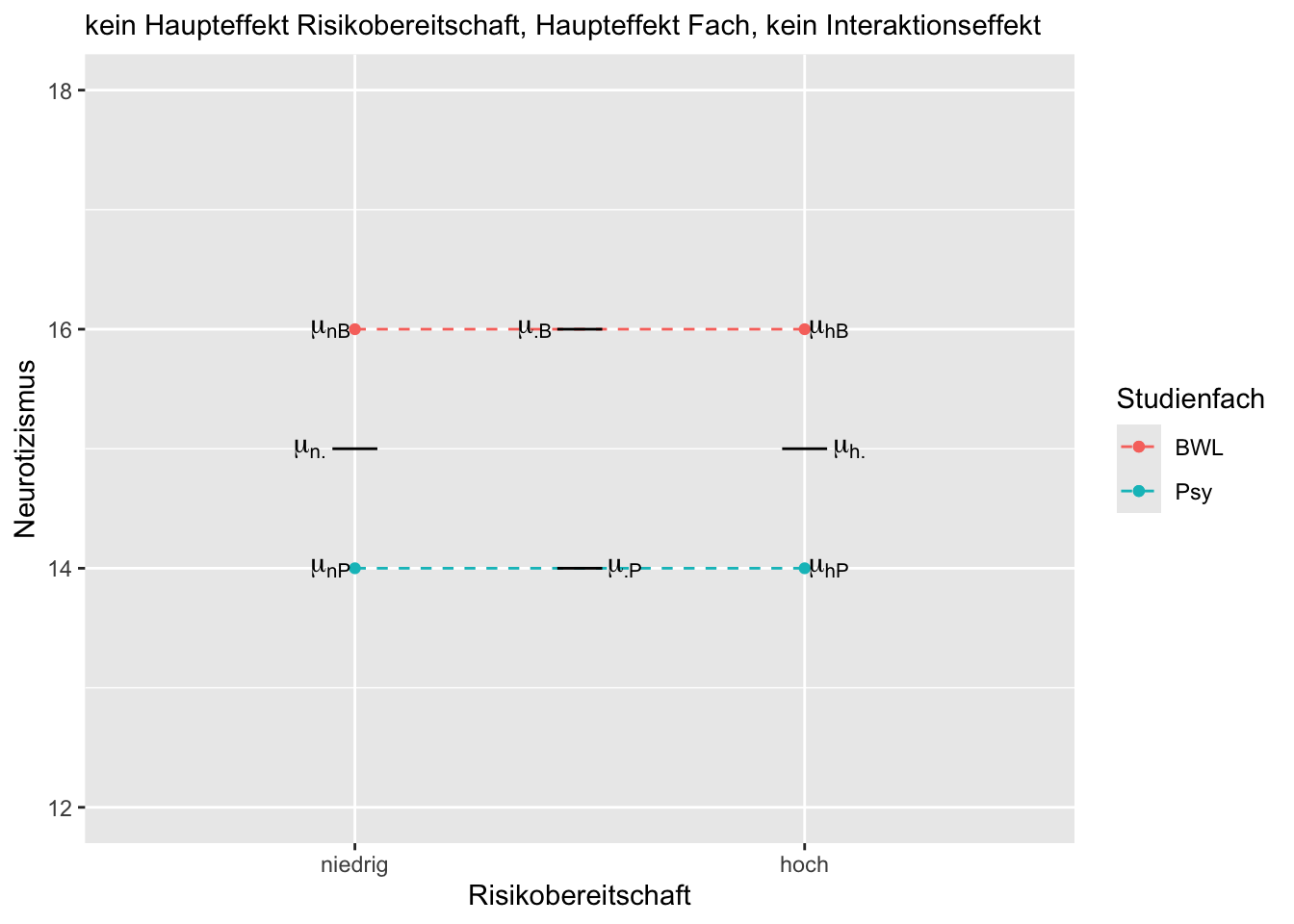
Erläuterung des oben gezeigten Beispiels:
Bei dem eingezeichneten Profilplot liegt keine Interaktion von Risikobereitschaft und Studienfach vor, da \(\mu_{nP} - \mu_{hP} = \mu_{nB} - \mu_{hB}\) bzw. \(\mu_{nP} - \mu_{nB}= \mu_{hP} - \mu_{hB}\). Es liegt ein Haupteffekt Studienfach vor, da \(\mu_{\cdot P} \neq \mu_{\cdot B}\). Es liegt kein Haupteffekt Risikobereitschaft vor, da \(\mu_{n \cdot} = \mu_{h \cdot}\).
Wichtig: Das ist natürlich nicht die einzige Möglichkeit eines Profilplots mit den gegebenen Anforderungen.
Sie untersuchen, ob der Einfluss der zweistufigen Variable Risikobereitschaft (hoch vs. niedrig) auf die (stetige) Variable Neurotizismus vom Studienfach (Psychologie vs. BWL) abhängt. Die Ergebnisse zeigen keinen Interaktionseffekt, einen Haupteffekt Risikobereitschaft und keinen Haupteffekt Studienfach. Zeichnen Sie in das nachfolgende Profildiagramm die Profillinien so ein, dass diese mit dem Ergebnis der Untersuchung nicht im Widerspruch stehen (Hinweis: möglicherweise gibt es mehr als eine richtige Lösung). Beschriften Sie dabei die x-Achse und die Profillinien und zeichnen Sie auch die Erwartungswerte \(\mu_{j \cdot}\) und \(\mu_{\cdot k}\) ein.
 TippLösung
TippLösung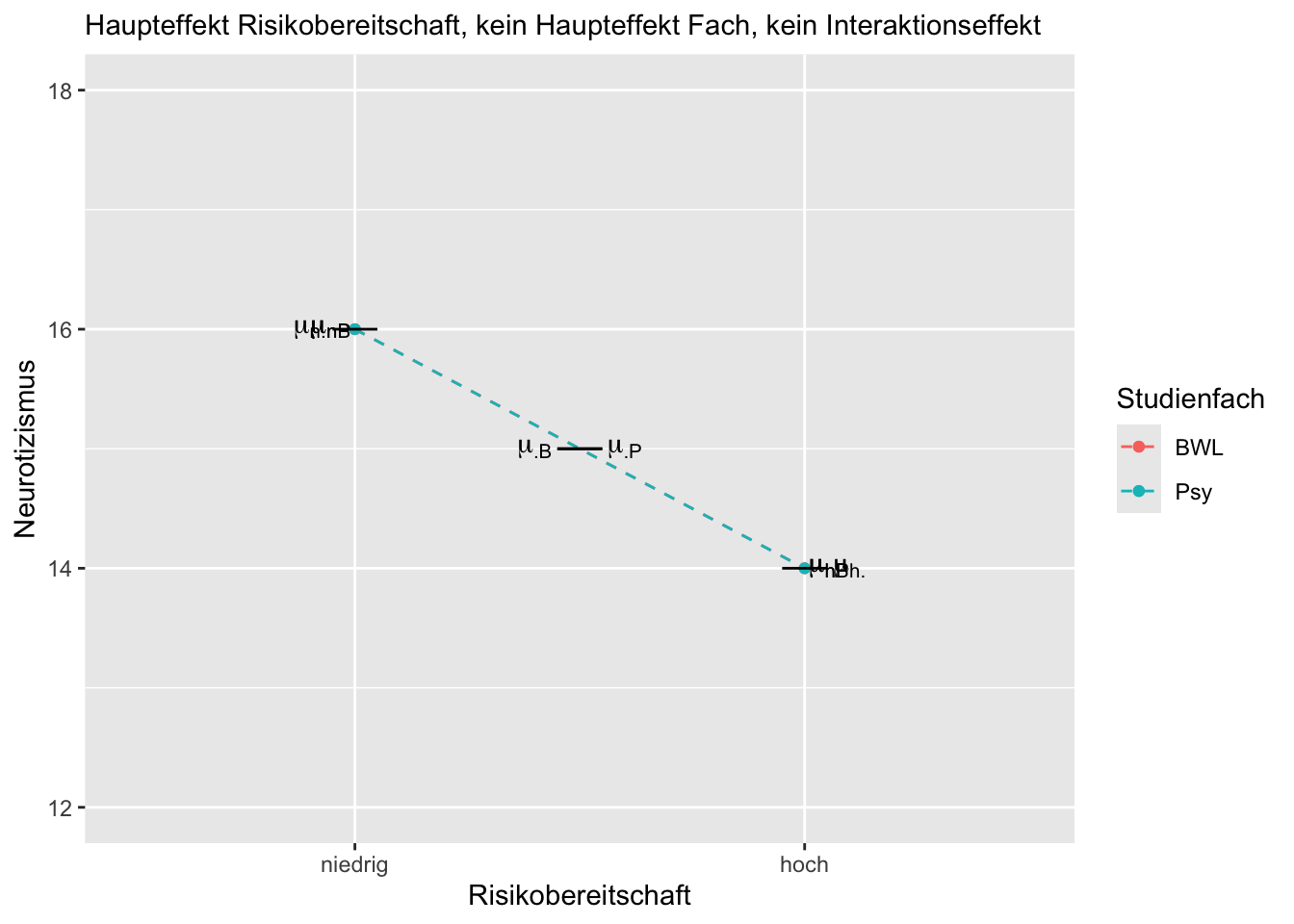
Erläuterung des oben gezeigten Beispiels:
Bei dem eingezeichneten Profilplot liegt keine Interaktion von Risikobereitschaft und Studienfach vor, da \(\mu_{nP} - \mu_{hP} = \mu_{nB} - \mu_{hB}\) bzw. \(\mu_{nP} - \mu_{nB}= \mu_{hP} - \mu_{hB}\). Es liegt kein Haupteffekt Studienfach vor, da \(\mu_{\cdot P} = \mu_{\cdot B}\). Es liegt ein Haupteffekt Risikobereitschaft vor, da \(\mu_{n \cdot} \neq \mu_{h \cdot}\).
Wichtig: Das ist natürlich nicht die einzige Möglichkeit eines Profilplots mit den gegebenen Anforderungen.
Sie untersuchen, ob der Einfluss der zweistufigen Variable Risikobereitschaft (hoch vs. niedrig) auf die (stetige) Variable Neurotizismus vom Studienfach (Psychologie vs. BWL) abhängt. Die Ergebnisse zeigen einen Interaktionseffekt, einen Haupteffekt Risikobereitschaft und einen Haupteffekt Studienfach. Zeichnen Sie in das nachfolgende Profildiagramm die Profillinien so ein, dass diese mit dem Ergebnis der Untersuchung nicht im Widerspruch stehen (Hinweis: möglicherweise gibt es mehr als eine richtige Lösung). Beschriften Sie dabei die x-Achse und die Profillinien und zeichnen Sie auch die Erwartungswerte \(\mu_{j \cdot}\) und \(\mu_{\cdot k}\) ein.
 TippLösung
TippLösung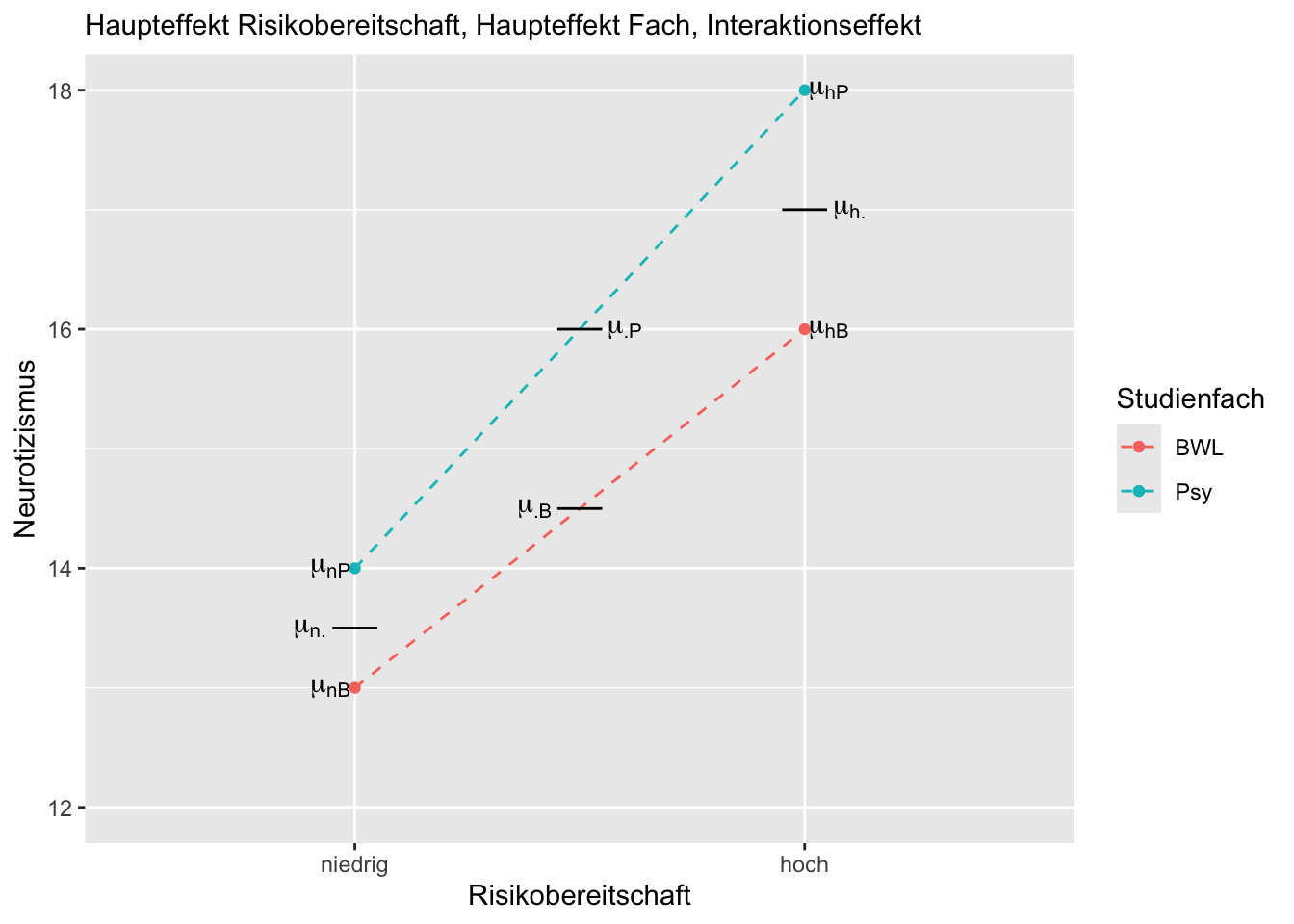
Erläuterung des oben gezeigten Beispiels:
Bei dem eingezeichneten Profilplot liegt eine Interaktion von Risikobereitschaft und Studienfach vor, da \(\mu_{nP} - \mu_{hP} \neq \mu_{nB} - \mu_{hB}\) bzw. \(\mu_{nP} - \mu_{nB}\neq \mu_{hP} - \mu_{hB}\). Es liegt ein Haupteffekt Studienfach vor, da \(\mu_{\cdot P} \neq \mu_{\cdot B}\). Es liegt ein Haupteffekt Risikobereitschaft vor, da \(\mu_{n \cdot} \neq \mu_{h \cdot}\).
Wichtig: Das ist natürlich nicht die einzige Möglichkeit eines Profilplots mit den gegebenen Anforderungen.
Sie untersuchen die Auswirkungen der Therapieformen Verhaltenstherapie und Psychoanalyse auf die mittlere (stetige) Symptomschwere von Patientinnen. Sie haben dafür auch eine Kontrollgruppe (KT = keine Therapie) erhoben, die keine von beiden Therapieformen erhalten hat. Es interessiert sie, ob sich die Therapieformen Verhaltenstherapie und Psychoanalyse in ihrer Auswirkung auf die Symptomschwere nach der Therapie von der Kontrollgruppe KT unterscheiden. Sie vermuten in beiden Fällen, dass sich die Symptomschwere nach der Therapie verringert.
Laden Sie den folgenden Datensatz herunter:
Testen Sie die interessierenden Größen (die Anleitung zur Durchführung von Einzelvergleichen in R finden Sie im Übungsblatt 5) und interpretieren Sie diese.
TippLösunglibrary(multcomp) ## Daten einlesen: Daten <- read.csv2("Daten1.csv"), stringsAsFactors = TRUE) ## aov-Objekt speichern: fit_aov <- aov(Symptomschwere ~ Therapieform, Daten) ## Wichtig: Exakte Namen der Faktorstufen verwenden! Zudem sollten die ## Namen der Faktorstufen keine Leer- oder Sonderzeichen enthalten. ## Sonst vorher umbenennen. Die Namen der Faktorstufen können ## Sie sich mithilfe der Funktion levels() ausgeben lassen: levels(Daten$Therapieform)[1] "KT" "Psychoanalyse" "Verhaltenstherapie"## Hypothesen für unser Beispiel: hyp1 <- 'Verhaltenstherapie - KT >= 0' hyp2 <- 'Psychoanalyse - KT >= 0' hyps <- c(hyp1, hyp2) kontraste <- mcp(Therapieform = hyps) fit <- glht(fit_aov, linfct = kontraste) summary(fit, test = univariate())Simultaneous Tests for General Linear Hypotheses Multiple Comparisons of Means: User-defined Contrasts Fit: aov(formula = as.formula(paste(c(AV, UV), collapse = " ~ ")), data = Daten) Linear Hypotheses: Estimate Std. Error t value Pr(<t) Verhaltenstherapie - KT >= 0 -9.850 2.426 -4.060 4.45e-05 *** Psychoanalyse - KT >= 0 -5.425 2.426 -2.236 0.0136 * --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 (Univariate p values reported)Wir gehen davon aus, dass Personen der Population die eine Verhaltenstherapie erhalten haben eine geringere mittlere Symptomschwere aufweisen als Personen der Kontrollgruppe.
Wir gehen davon aus, dass Personen der Population die eine Psychoanalyse erhalten haben keine geringere mittlere Symptomschwere aufweisen als Personen der Kontrollgruppe.
Sie untersuchen die Auswirkungen der Therapieformen Verhaltenstherapie und Psychoanalyse auf die mittlere (stetige) Symptomschwere von Patientinnen. Sie haben dafür auch eine Kontrollgruppe (KT = keine Therapie) erhoben, die keine von beiden Therapieformen erhalten hat. Es interessiert sie, wie stark sich die Therapieformen Verhaltenstherapie und Psychoanalyse in ihrer Auswirkung auf die Symptomschwere nach der Therapie von der Kontrollgruppe KT unterscheiden.
Laden Sie den folgenden Datensatz herunter:
Berechnen Sie 95%-Konfidenzintervalle für die interessierenden Größen (die Anleitung zur Durchführung von Einzelvergleichen in R finden Sie im Übungsblatt 5) und interpretieren Sie diese.
TippLösunglibrary(multcomp) ## Daten einlesen: Daten <- read.csv2("Daten2.csv"), stringsAsFactors = TRUE) ## aov-Objekt speichern: fit_aov <- aov(Symptomschwere ~ Therapieform, Daten) ## Wichtig: Exakte Namen der Faktorstufen verwenden! Zudem sollten die ## Namen der Faktorstufen keine Leer- oder Sonderzeichen enthalten. ## Sonst vorher umbenennen. Die Namen der Faktorstufen können ## Sie sich mithilfe der Funktion levels() ausgeben lassen: levels(Daten$Therapieform)[1] "KT" "Psychoanalyse" "Verhaltenstherapie"## Hypothesen für unser Beispiel: hyp1 <- 'Verhaltenstherapie - KT == 0' hyp2 <- 'Psychoanalyse - KT == 0' hyps <- c(hyp1, hyp2) kontraste <- mcp(Therapieform = hyps) fit <- glht(fit_aov, linfct = kontraste) confint(fit, level = 0.95, calpha = univariate_calpha())Simultaneous Confidence Intervals Multiple Comparisons of Means: User-defined Contrasts Fit: aov(formula = as.formula(paste(c(AV, UV), collapse = " ~ ")), data = Daten) Quantile = 1.9804 95% confidence level Linear Hypotheses: Estimate lwr upr Verhaltenstherapie - KT == 0 -6.3250 -11.0576 -1.5924 Psychoanalyse - KT == 0 -5.9500 -10.6826 -1.2174Wir gehen davon aus, dass plausible Werte für den Unterschied der mittleren Symptomschwere zwischen Personen der Population die eine Verhaltenstherapie erhalten haben und Personen der Kontrollgruppe zwischen -11.06 und -1.59 liegen.
Wir gehen davon aus, dass plausible Werte für den Unterschied der mittleren Depressionsschwere zwischen Personen der Population die eine Psychoanalyse erhalten haben und Personen der Kontrollgruppe zwischen -10.68 und -1.22 liegen.
Sie untersuchen die Auswirkungen der Therapieformen Physiotherapie und Osteopathie auf die mittlere (stetige) Symptomschwere von Patientinnen. Sie haben dafür auch eine Kontrollgruppe (KT = keine Therapie) erhoben, die keine von beiden Therapieformen erhalten hat. Es interessiert sie, wie stark sich die Therapieformen Physiotherapie und Osteopathie in ihrer Auswirkung auf die Symptomschwere nach der Therapie von der Kontrollgruppe KT unterscheiden.
Laden Sie den folgenden Datensatz herunter:
Berechnen Sie 95%-Konfidenzintervalle für die interessierenden Größen (die Anleitung zur Durchführung von Einzelvergleichen in R finden Sie im Übungsblatt 5) und interpretieren Sie diese.
TippLösunglibrary(multcomp) ## Daten einlesen: Daten <- read.csv2("Daten3.csv"), stringsAsFactors = TRUE) ## aov-Objekt speichern: fit_aov <- aov(Symptomschwere ~ Therapieform, Daten) ## Wichtig: Exakte Namen der Faktorstufen verwenden! Zudem sollten die ## Namen der Faktorstufen keine Leer- oder Sonderzeichen enthalten. ## Sonst vorher umbenennen. Die Namen der Faktorstufen können ## Sie sich mithilfe der Funktion levels() ausgeben lassen: levels(Daten$Therapieform)[1] "KT" "Osteopathie" "Physiotherapie"## Hypothesen für unser Beispiel: hyp1 <- 'Physiotherapie - KT == 0' hyp2 <- 'Osteopathie - KT == 0' hyps <- c(hyp1, hyp2) kontraste <- mcp(Therapieform = hyps) fit <- glht(fit_aov, linfct = kontraste) confint(fit, level = 0.95, calpha = univariate_calpha())Simultaneous Confidence Intervals Multiple Comparisons of Means: User-defined Contrasts Fit: aov(formula = as.formula(paste(c(AV, UV), collapse = " ~ ")), data = Daten) Quantile = 1.9804 95% confidence level Linear Hypotheses: Estimate lwr upr Physiotherapie - KT == 0 -9.3750 -13.8645 -4.8855 Osteopathie - KT == 0 -10.1250 -14.6145 -5.6355Wir gehen davon aus, dass plausible Werte für den Unterschied der mittleren Symptomschwere zwischen Personen der Population die eine Physiotherapie erhalten haben und Personen der Kontrollgruppe zwischen -13.86 und -4.89 liegen.
Wir gehen davon aus, dass plausible Werte für den Unterschied der mittleren Depressionsschwere zwischen Personen der Population die eine Osteopathie erhalten haben und Personen der Kontrollgruppe zwischen -14.61 und -5.64 liegen.
Sie untersuchen die Auswirkungen der Therapieformen Verhaltenstherapie und Psychoanalyse auf die mittlere (stetige) Symptomschwere von Patientinnen. Sie haben dafür auch eine Kontrollgruppe (KT = keine Therapie) erhoben, die keine von beiden Therapieformen erhalten hat. Es interessiert sie, ob sich die Therapieformen Verhaltenstherapie und Psychoanalyse in ihrer Auswirkung auf die Symptomschwere nach der Therapie von der Kontrollgruppe KT unterscheiden.
Laden Sie den folgenden Datensatz herunter:
Testen Sie die interessierenden Größen (die Anleitung zur Durchführung von Einzelvergleichen in R finden Sie im Übungsblatt 5) und interpretieren Sie diese.
TippLösunglibrary(multcomp) ## Daten einlesen: Daten <- read.csv2("Daten4.csv"), stringsAsFactors = TRUE) ## aov-Objekt speichern: fit_aov <- aov(Symptomschwere ~ Therapieform, Daten) ## Wichtig: Exakte Namen der Faktorstufen verwenden! Zudem sollten die ## Namen der Faktorstufen keine Leer- oder Sonderzeichen enthalten. ## Sonst vorher umbenennen. Die Namen der Faktorstufen können ## Sie sich mithilfe der Funktion levels() ausgeben lassen: levels(Daten$Therapieform)[1] "KT" "Psychoanalyse" "Verhaltenstherapie"## Hypothesen für unser Beispiel: hyp1 <- 'Verhaltenstherapie - KT == 0' hyp2 <- 'Psychoanalyse - KT == 0' hyps <- c(hyp1, hyp2) kontraste <- mcp(Therapieform = hyps) fit <- glht(fit_aov, linfct = kontraste) summary(fit, test = univariate())Simultaneous Tests for General Linear Hypotheses Multiple Comparisons of Means: User-defined Contrasts Fit: aov(formula = as.formula(paste(c(AV, UV), collapse = " ~ ")), data = Daten) Linear Hypotheses: Estimate Std. Error t value Pr(>|t|) Verhaltenstherapie - KT == 0 -5.575 2.217 -2.514 0.01328 * Psychoanalyse - KT == 0 -7.175 2.217 -3.236 0.00158 ** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 (Univariate p values reported)Wir gehen davon aus, dass Personen der Population die eine Verhaltenstherapie erhalten haben keine unterschiedliche mittlere Symptomschwere aufweisen als Personen der Kontrollgruppe.
Wir gehen davon aus, dass Personen der Population die eine Psychoanalyse erhalten haben eine unterschiedliche mittlere Symptomschwere aufweisen als Personen der Kontrollgruppe.
Sie untersuchen die Auswirkungen der Therapieformen Verhaltenstherapie und Psychoanalyse auf die mittlere (stetige) Symptomschwere von Patientinnen. Sie haben dafür auch eine Kontrollgruppe (KT = keine Therapie) erhoben, die keine von beiden Therapieformen erhalten hat. Es interessiert sie, wie stark sich die Therapieformen Verhaltenstherapie und Psychoanalyse in ihrer Auswirkung auf die Symptomschwere nach der Therapie von der Kontrollgruppe KT unterscheiden.
Laden Sie den folgenden Datensatz herunter:
Berechnen Sie 95%-Konfidenzintervalle für die interessierenden Größen (die Anleitung zur Durchführung von Einzelvergleichen in R finden Sie im Übungsblatt 5) und interpretieren Sie diese.
TippLösunglibrary(multcomp) ## Daten einlesen: Daten <- read.csv2("Daten5.csv"), stringsAsFactors = TRUE) ## aov-Objekt speichern: fit_aov <- aov(Symptomschwere ~ Therapieform, Daten) ## Wichtig: Exakte Namen der Faktorstufen verwenden! Zudem sollten die ## Namen der Faktorstufen keine Leer- oder Sonderzeichen enthalten. ## Sonst vorher umbenennen. Die Namen der Faktorstufen können ## Sie sich mithilfe der Funktion levels() ausgeben lassen: levels(Daten$Therapieform)[1] "KT" "Psychoanalyse" "Verhaltenstherapie"## Hypothesen für unser Beispiel: hyp1 <- 'Verhaltenstherapie - KT == 0' hyp2 <- 'Psychoanalyse - KT == 0' hyps <- c(hyp1, hyp2) kontraste <- mcp(Therapieform = hyps) fit <- glht(fit_aov, linfct = kontraste) confint(fit, level = 0.95, calpha = univariate_calpha())Simultaneous Confidence Intervals Multiple Comparisons of Means: User-defined Contrasts Fit: aov(formula = as.formula(paste(c(AV, UV), collapse = " ~ ")), data = Daten) Quantile = 1.9804 95% confidence level Linear Hypotheses: Estimate lwr upr Verhaltenstherapie - KT == 0 -6.3250 -10.5403 -2.1097 Psychoanalyse - KT == 0 -9.2000 -13.4153 -4.9847Wir gehen davon aus, dass plausible Werte für den Unterschied der mittleren Symptomschwere zwischen Personen der Population die eine Verhaltenstherapie erhalten haben und Personen der Kontrollgruppe zwischen -10.54 und -2.11 liegen.
Wir gehen davon aus, dass plausible Werte für den Unterschied der mittleren Depressionsschwere zwischen Personen der Population die eine Psychoanalyse erhalten haben und Personen der Kontrollgruppe zwischen -13.42 und -4.98 liegen.
Sie untersuchen die Auswirkungen der Therapieformen Musiktherapie und Maltherapie auf die mittlere (stetige) Symptomschwere von Patientinnen. Sie haben dafür auch eine Kontrollgruppe (KT = keine Therapie) erhoben, die keine von beiden Therapieformen erhalten hat. Es interessiert sie, ob sich die Therapieformen Musiktherapie und Maltherapie in ihrer Auswirkung auf die Symptomschwere nach der Therapie von der Kontrollgruppe KT unterscheiden. Sie vermuten in beiden Fällen, dass sich die Symptomschwere nach der Therapie verringert.
Laden Sie den folgenden Datensatz herunter:
Testen Sie die interessierenden Größen (die Anleitung zur Durchführung von Einzelvergleichen in R finden Sie im Übungsblatt 5) und interpretieren Sie diese.
TippLösunglibrary(multcomp) ## Daten einlesen: Daten <- read.csv2("Daten6.csv"), stringsAsFactors = TRUE) ## aov-Objekt speichern: fit_aov <- aov(Symptomschwere ~ Therapieform, Daten) ## Wichtig: Exakte Namen der Faktorstufen verwenden! Zudem sollten die ## Namen der Faktorstufen keine Leer- oder Sonderzeichen enthalten. ## Sonst vorher umbenennen. Die Namen der Faktorstufen können ## Sie sich mithilfe der Funktion levels() ausgeben lassen: levels(Daten$Therapieform)[1] "KT" "Maltherapie" "Musiktherapie"## Hypothesen für unser Beispiel: hyp1 <- 'Musiktherapie - KT >= 0' hyp2 <- 'Maltherapie - KT >= 0' hyps <- c(hyp1, hyp2) kontraste <- mcp(Therapieform = hyps) fit <- glht(fit_aov, linfct = kontraste) summary(fit, test = univariate())Simultaneous Tests for General Linear Hypotheses Multiple Comparisons of Means: User-defined Contrasts Fit: aov(formula = as.formula(paste(c(AV, UV), collapse = " ~ ")), data = Daten) Linear Hypotheses: Estimate Std. Error t value Pr(<t) Musiktherapie - KT >= 0 -8.250 2.054 -4.016 5.25e-05 *** Maltherapie - KT >= 0 -4.950 2.054 -2.410 0.00877 ** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 (Univariate p values reported)Wir gehen davon aus, dass Personen der Population die eine Musiktherapie erhalten haben eine geringere mittlere Symptomschwere aufweisen als Personen der Kontrollgruppe.
Wir gehen davon aus, dass Personen der Population die eine Maltherapie erhalten haben keine geringere mittlere Symptomschwere aufweisen als Personen der Kontrollgruppe.
Sie untersuchen die Auswirkungen der Therapieformen Physiotherapie und Osteopathie auf die mittlere (stetige) Symptomschwere von Patientinnen. Sie haben dafür auch eine Kontrollgruppe (KT = keine Therapie) erhoben, die keine von beiden Therapieformen erhalten hat. Es interessiert sie, ob sich die Therapieformen Physiotherapie und Osteopathie in ihrer Auswirkung auf die Symptomschwere nach der Therapie von der Kontrollgruppe KT unterscheiden.
Laden Sie den folgenden Datensatz herunter:
Testen Sie die interessierenden Größen (die Anleitung zur Durchführung von Einzelvergleichen in R finden Sie im Übungsblatt 5) und interpretieren Sie diese.
TippLösunglibrary(multcomp) ## Daten einlesen: Daten <- read.csv2("Daten7.csv"), stringsAsFactors = TRUE) ## aov-Objekt speichern: fit_aov <- aov(Symptomschwere ~ Therapieform, Daten) ## Wichtig: Exakte Namen der Faktorstufen verwenden! Zudem sollten die ## Namen der Faktorstufen keine Leer- oder Sonderzeichen enthalten. ## Sonst vorher umbenennen. Die Namen der Faktorstufen können ## Sie sich mithilfe der Funktion levels() ausgeben lassen: levels(Daten$Therapieform)[1] "KT" "Osteopathie" "Physiotherapie"## Hypothesen für unser Beispiel: hyp1 <- 'Physiotherapie - KT == 0' hyp2 <- 'Osteopathie - KT == 0' hyps <- c(hyp1, hyp2) kontraste <- mcp(Therapieform = hyps) fit <- glht(fit_aov, linfct = kontraste) summary(fit, test = univariate())Simultaneous Tests for General Linear Hypotheses Multiple Comparisons of Means: User-defined Contrasts Fit: aov(formula = as.formula(paste(c(AV, UV), collapse = " ~ ")), data = Daten) Linear Hypotheses: Estimate Std. Error t value Pr(>|t|) Physiotherapie - KT == 0 -4.275 2.013 -2.124 0.0358 * Osteopathie - KT == 0 -5.075 2.013 -2.521 0.0131 * --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 (Univariate p values reported)Wir gehen davon aus, dass Personen der Population die eine Physiotherapie erhalten haben keine unterschiedliche mittlere Symptomschwere aufweisen als Personen der Kontrollgruppe.
Wir gehen davon aus, dass Personen der Population die eine Osteopathie erhalten haben keine unterschiedliche mittlere Symptomschwere aufweisen als Personen der Kontrollgruppe.
Sie untersuchen die Auswirkungen der Therapieformen Physiotherapie und Osteopathie auf die mittlere (stetige) Symptomschwere von Patientinnen. Sie haben dafür auch eine Kontrollgruppe (KT = keine Therapie) erhoben, die keine von beiden Therapieformen erhalten hat. Es interessiert sie, wie stark sich die Therapieformen Physiotherapie und Osteopathie in ihrer Auswirkung auf die Symptomschwere nach der Therapie von der Kontrollgruppe KT unterscheiden.
Laden Sie den folgenden Datensatz herunter:
Berechnen Sie 95%-Konfidenzintervalle für die interessierenden Größen (die Anleitung zur Durchführung von Einzelvergleichen in R finden Sie im Übungsblatt 5) und interpretieren Sie diese.
TippLösunglibrary(multcomp) ## Daten einlesen: Daten <- read.csv2("Daten8.csv"), stringsAsFactors = TRUE) ## aov-Objekt speichern: fit_aov <- aov(Symptomschwere ~ Therapieform, Daten) ## Wichtig: Exakte Namen der Faktorstufen verwenden! Zudem sollten die ## Namen der Faktorstufen keine Leer- oder Sonderzeichen enthalten. ## Sonst vorher umbenennen. Die Namen der Faktorstufen können ## Sie sich mithilfe der Funktion levels() ausgeben lassen: levels(Daten$Therapieform)[1] "KT" "Osteopathie" "Physiotherapie"## Hypothesen für unser Beispiel: hyp1 <- 'Physiotherapie - KT == 0' hyp2 <- 'Osteopathie - KT == 0' hyps <- c(hyp1, hyp2) kontraste <- mcp(Therapieform = hyps) fit <- glht(fit_aov, linfct = kontraste) confint(fit, level = 0.95, calpha = univariate_calpha())Simultaneous Confidence Intervals Multiple Comparisons of Means: User-defined Contrasts Fit: aov(formula = as.formula(paste(c(AV, UV), collapse = " ~ ")), data = Daten) Quantile = 1.9804 95% confidence level Linear Hypotheses: Estimate lwr upr Physiotherapie - KT == 0 -6.7000 -10.9588 -2.4412 Osteopathie - KT == 0 -9.6500 -13.9088 -5.3912Wir gehen davon aus, dass plausible Werte für den Unterschied der mittleren Symptomschwere zwischen Personen der Population die eine Physiotherapie erhalten haben und Personen der Kontrollgruppe zwischen -10.96 und -2.44 liegen.
Wir gehen davon aus, dass plausible Werte für den Unterschied der mittleren Depressionsschwere zwischen Personen der Population die eine Osteopathie erhalten haben und Personen der Kontrollgruppe zwischen -13.91 und -5.39 liegen.