Arbeitsauftrag: Exploratorische Faktorenanalyse

Tutorialreihe zum UK Fragebogenentwicklung

1. Arbeitsauftrag: Konfirmatorische Faktorenanalyse
2. Arbeitsauftrag: Exploratorische Faktorenanalyse
3. Arbeitsauftrag: Reliabilität und Validität

1 Einführung

In diesem Tutorial werden Sie darauf vorbereitet, wie Sie die Daten aus Ihrem im UK erstellten Fragebogen mithilfe einer Exploratorischen Faktorenanalyse (EFA) in R auswerten können. Dazu arbeiten wir zunächst wieder mit demselben Beispieldatensatz wie im Arbeitsauftrag: Konfirmatorische Faktorenanalyse.

Wir werden die EFA zunächst einmal gemeinsam durcharbeiten, bevor Sie den vollständigen Ablauf dann eigenständig im Arbeitsauftrag anwenden.

1.1 Vorbereitung in R

Bitte führen Sie nun folgende Schritte aus, um unser Skript für die Analyse vorzubereiten:

1. Öffnen Sie Ihr RStudio Projekt für das UK Fragebogenentwicklung.

2. Legen Sie ein neues R Skript an und speichern Sie es in dem Ordner, in dem Ihr RStudio Projekt, z. B. unter dem Namen EFA, ab.

3. Laden Sie die Pakete, die wir für die EFA benötigen

   library(psych) # für EFA 
   install.packages("GPArotation") # für manche Rotationen

   Hinweis: Das Paket “GPArotation” muss installiert, aber nicht geladen werden.

4. Laden Sie den Datensatz

   neo <- read.csv("NEO_original.csv")

5. Extraversionsitems auswählen

   Wir konzentrieren uns erneut auf die Extraversionsitems und filtern den Datensatz so, dass er nur noch diese enthält. Dazu erstellen wir einen Vektor mit den Spaltennamen der Extraversionsitems:

   extra_items <- c("E1", "E2", "E3", "E4", "E5", "E6", 
                    "E7", "E8", "E9", "E10", "E11", "E12")
   neo_extra <- neo[, extra_items]

   Mit neo[, extra_items] filtern wir die entsprechenden Spalten aus dem Datensatz. Damit enthält der Datensatz neo_extra alle Zeilen, aber nur noch die 12 Spalten (d.h., Variablen), welche die Extraversionsitems repräsentieren. Mit dem Befehl str(neo_extra) können wir überprüfen, ob der Datensatz die erwartete Form besitzt.

2 Exploratorische Faktorenanalyse (EFA)

2.1 Ziel der EFA

In diesem Abschnitt führen wir eine Exploratorische Faktorenanalyse (EFA) mit dem {psych} Paket in R durch. Ziel ist es, die zugrundeliegende Anzahl an latenten Variablen für die Extraversionsitems E1, E2, …, E12 zu bestimmen, im Anschluss ein mehrdimensionales \(\tau\)-kongenerisches Modell zu schätzen und die Zuordnung der Items zu den Faktoren explorativ zu untersuchen und inhaltlich zu interpretieren.

2.2 Schritte der EFA

1. Bestimmung der Anzahl an latenten Variablen

Parallelanalyse durchführen

Die Parallelanalyse hilft uns, datengetrieben abzuschätzen, wie viele Faktoren (latente Variablen) hinter den Items stecken könnten. Wir vermuten hier aus theoretischer Sicht, dass ein Faktor (Extraversion) die 12 Items erklärt. Die Parallelanalyse prüft jedoch, ob vielleicht doch mehrere Faktoren vorliegen.

Hinweis

Die Parallelanalyse vergleicht die empirisch beobachteten Eigenwerte der Faktoren im Datensatz mit simulierten zufallsbedingten Eigenwerten. Diese zufallsbedingten Eigenwerte basieren auf simulierten Datensätzen, welche die gleiche Größe wie der echte Datensatz haben, in denen jedoch keine systematischen Zusammenhänge zwischen den Items bestehen. Dadurch dienen sie als Referenz für rein zufällige Faktorenstrukturen. Diese Simulation wird mehrfach wiederholt, um eine Verteilung der zufallsbedingten Eigenwerte pro Faktor zu erhalten, auf deren Basis die kritischen Eigenwerte bestimmt werden können (z.B. am 95%-Quantil). Zufallsbedingte Eigenwerte liegen dann in nur 5% der Fälle über den kritischen Eigenwerten. Liegt der empirisch beobachtete Eigenwert eines Faktors also über dem kritischen Eigenwert ist es unwahrscheinlich, dass er durch Zufall entstanden ist und wird als realer (d.h. tatsächlich vorliegender) Faktor angenommen.

Befehl für die Parallelanalyse:

fa.parallel(
1  neo_extra,
2  fa = "fa",
3  fm = "ml",
4  quant = 0.95,
5  n.iter = 1000
)

1

neo_extra: Wir übergeben den Datensatz, der nur die 12 Extraversionsitems enthält.

2

fa = "fa": Wir geben an, dass wir eine Faktorenanalyse (statt z.B. principle component analysis) durchführen wollen.

3

fm = "ml": Wir spezifizieren „Maximum Likelihood“ als Schätzmethode.

4

quant = 0.95: Wir legen für den Test der einzelnen Eigenwerte das Signifikanzniveau auf 5% fest, indem wir das Quantil angeben, an dem die kritischen Eigenwerte liegen. D.h., hier werden die empirisch beobachteten Eigenwerte mit den simulierten Eigenwerten am 95%-Quantil verglichen.

5

n.iter = 1000: Wir geben an, wie oft zufällige Datensätze simuliert werden sollen um den kritischen Eigenwert zu bestimmen (für robuste Ergebnisse sollte eine hohe Zahl gewählt werden).

Output anzeigen

fa.parallel(neo_extra, fa = "fa", fm = "ml", quant = 0.95, n.iter = 1000)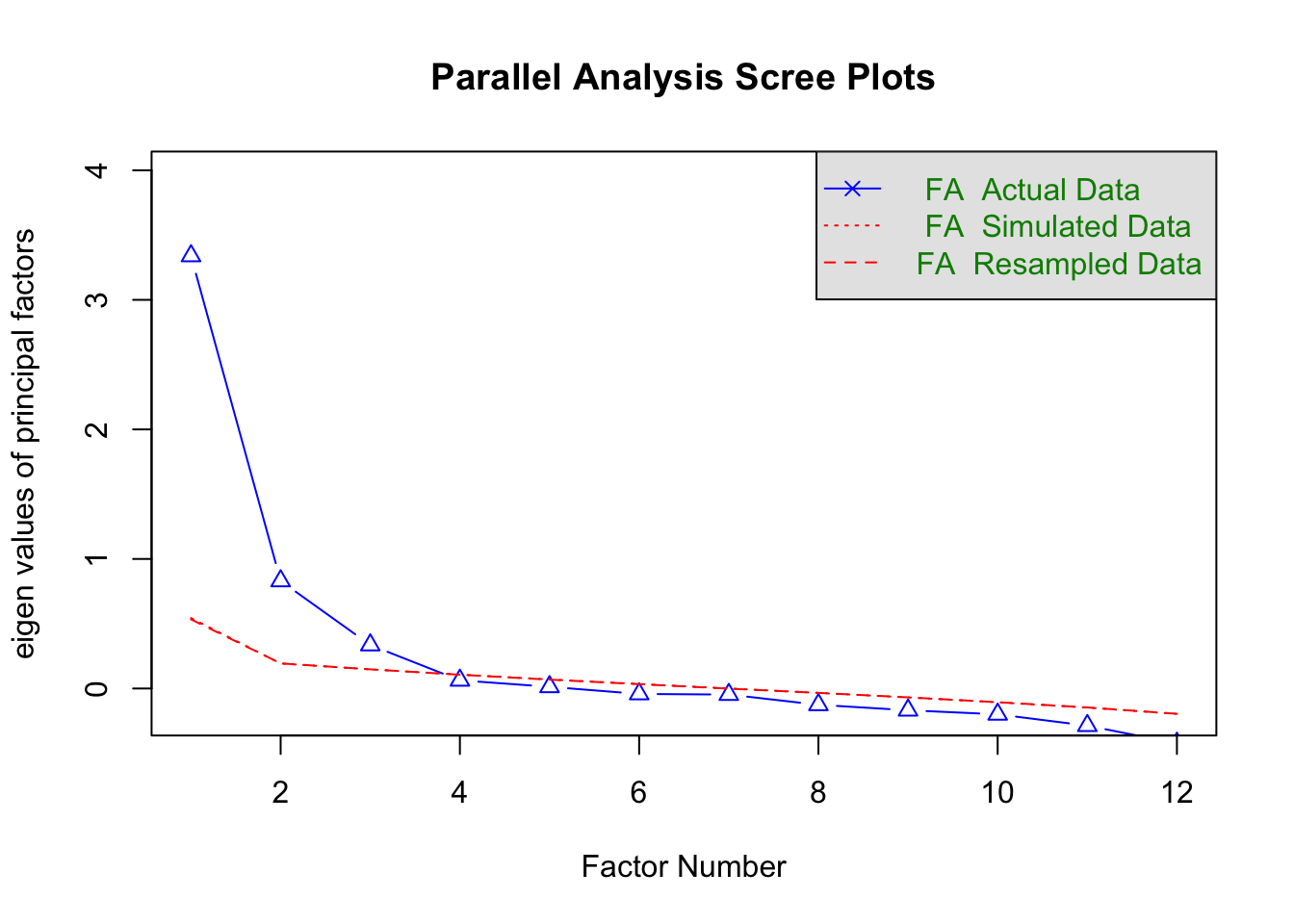

Parallel analysis suggests that the number of factors =  3  and the number of components =  NA 

Ausgabe verstehen:

Der Befehl gibt einen Text-Output in der Konsole und ein Diagramm im Plots-Fenster aus.

In der Konsole lesen Sie:

Parallel analysis suggests that the number of factors =  3  and the number of components =  NA 

Das bedeutet: Die Parallelanalyse geht davon aus, dass drei Faktoren hinter unseren Extraversionsitems stecken – und nicht nur eine latente Variable, wie wir vielleicht erwartet hätten.

Im Plot der Parallelanalyse vergleichen wir die blauen Dreiecke (empirisch beobachtete Eigenwerte) mit der roten Linie (95%-Quantil der simulierten Eigenwerte). Diese Werte helfen uns zu entscheiden, wie viele Faktoren tatsächlich „real“ sind und wie viele lediglich zufällige Effekte darstellen könnten.

• Blaues Dreieck > Rote Linie: Ein Faktor wird als „real“ interpretiert. Das bedeutet, der Eigenwert des Faktors ist signifikant höher als zufällig simulierte Eigenwerte.
• Blaues Dreieck ≤ Rote Linie: Ein Faktor wird als “nicht real” interpretiert. Hier könnte der beobachtete Eigenwert auch durch Zufall entstanden sein.

Hinweis

Die rote Linie besteht eigentlich aus zwei Linien, die in der Legende erklärt werden: Eine für die Methode des „Resamplings“ und eine für die Methode der „Simulation“. Dabei handelt es sich um zwei verschiedene Ansätze um die simulierten Datensätze zu generieren. Beide Methoden führen praktisch immer zum gleichen Ergebnis, sodass der Unterschied in der Darstellung vernachlässigbar ist.

Faktor 1: Das erste blaue Dreieck (der beobachtete Eigenwert des ersten Faktors) liegt deutlich über der roten Linie, das heißt:

• Der Eigenwert des ersten Faktors ist signifikant höher, als es durch Zufall zu erwarten wäre.
• Wir interpretieren den ersten Faktor als „real“.

Faktor 2: Auch das zweite blaue Dreieck liegt oberhalb der roten Linie. Dies deutet darauf hin, dass auch der zweite Faktor real ist. Die Daten enthalten mindestens zwei latente Dimensionen.

Faktor 3: Beim dritten Faktor zeigt der Plot dasselbe Muster: Das blaue Dreieck liegt erneut über der roten Linie. Wir schließen, dass auch der dritte Faktor signifikant ist und daher nicht durch Zufall erklärt werden kann.

Faktor 4: Beim vierten Faktor ist das blaue Dreieck unterhalb der roten Linie. Das bedeutet:

• Der beobachtete Eigenwert des vierten Faktors könnte durch Zufall entstanden sein.
• Wir interpretieren den vierten Faktor als zufälligen Effekt und als nicht real.

Ergebnis der Parallelanalyse

Die Parallelanalyse legt als insgesamt nahe, dass drei Faktoren die Datenstruktur am besten beschreiben. Dieses Ergebnis liefert einen datengetriebenen Ansatz zur Entscheidung über die Anzahl der latenten Variablen.

2. Spezifikation des Testmodells

In der EFA wird stets ein ein- bzw. mehrdimensionales \(\tau\)-kongenerisches Modell untersucht. Die Parallelanalyse hat ergeben, dass drei Faktoren die Datenstruktur am besten beschreiben. Wir werden daher im Anschluss ein mehrdimensionales \(\tau\)-kongenerisches Modell mit 3 Faktoren betrachten.

3. Schätzung des Testmodells

EFA durchführen

Nachdem wir mithilfe der Parallelanalyse die Anzahl an latenten Variablen bestimmt haben, können wir jetzt die Exploratorische Faktorenanalyse (EFA) durchführen.

Der zentrale Befehl für die EFA lautet:

fa(
1  neo_extra,
2  fm = "ml",
3  rotate = "Promax",
4  nfactors = 3,
5  scores = "Bartlett"
)

1

neo_extra: Wir übergeben den Datensatz, der nur die 12 Extraversionsitems enthält.

2

fm = "ml": Wir spezifizieren „Maximum Likelihood“ als Schätzmethode.

3

rotate = "Promax": Die Rotation macht die Faktorenstruktur interpretierbarer. Die „Promax“-Rotation ist eine oblique Rotationsmethode, d. h., die Faktoren dürfen miteinander korrelieren.

4

nfactors = 3: Hier legen wir die Anzahl der Faktoren fest, basierend auf dem Ergebnis der Parallelanalyse.

5

scores = "Bartlett": Mit der „Bartlett“-Methode könnten später Werte für die latenten Variablen geschätzt werden (z.B. für Einzelfalldiagnostik).

Output anzeigen

fa(neo_extra, fm = "ml", rotate = "Promax", nfactors = 3, scores = "Bartlett")

Factor Analysis using method =  ml
Call: fa(r = neo_extra, nfactors = 3, rotate = "Promax", scores = "Bartlett", 
    fm = "ml")
Standardized loadings (pattern matrix) based upon correlation matrix
      ML1   ML2   ML3   h2   u2 com
E1   0.02  0.33  0.50 0.55 0.45 1.7
E2   0.55 -0.14  0.07 0.28 0.72 1.2
E3   0.77 -0.09  0.04 0.56 0.44 1.0
E4   0.12  0.19  0.42 0.39 0.61 1.6
E5  -0.06  0.74 -0.06 0.47 0.53 1.0
E6  -0.08 -0.20  0.80 0.46 0.54 1.2
E7   0.39  0.28 -0.10 0.28 0.72 2.0
E8   0.92 -0.05 -0.04 0.77 0.23 1.0
E9   0.70  0.02 -0.02 0.48 0.52 1.0
E10 -0.25  0.57 -0.04 0.23 0.77 1.4
E11  0.30  0.39 -0.07 0.31 0.69 1.9
E12  0.00  0.24  0.32 0.24 0.76 1.8

                       ML1  ML2  ML3
SS loadings           2.49 1.34 1.20
Proportion Var        0.21 0.11 0.10
Cumulative Var        0.21 0.32 0.42
Proportion Explained  0.49 0.27 0.24
Cumulative Proportion 0.49 0.76 1.00

 With factor correlations of 
     ML1  ML2  ML3
ML1 1.00 0.50 0.51
ML2 0.50 1.00 0.54
ML3 0.51 0.54 1.00

Mean item complexity =  1.4
Test of the hypothesis that 3 factors are sufficient.

df null model =  66  with the objective function =  3.23 with Chi Square =  1808.61
df of  the model are 33  and the objective function was  0.17 

The root mean square of the residuals (RMSR) is  0.03 
The df corrected root mean square of the residuals is  0.04 

The harmonic n.obs is  566 with the empirical chi square  70.96  with prob <  0.00014 
The total n.obs was  566  with Likelihood Chi Square =  92.37  with prob <  1.6e-07 

Tucker Lewis Index of factoring reliability =  0.932
RMSEA index =  0.056  and the 90 % confidence intervals are  0.043 0.07
BIC =  -116.8
Fit based upon off diagonal values = 0.99
Measures of factor score adequacy             
                                                   ML1  ML2  ML3
Correlation of (regression) scores with factors   0.94 0.85 0.85
Multiple R square of scores with factors          0.87 0.73 0.73
Minimum correlation of possible factor scores     0.75 0.46 0.45

4. Evaluation der Modellpassung

Auch wenn es möglich ist, für ein mit der EFA geschätztes Testmodell Modelltests und Fit-Indizes zu berechnen, werden wir dies hier nicht betrachten, da ein Test der Modellpassung dem Grundgedanken einer exploratorischen Analyse eher widerspricht und eigentlich Ziel der CFA ist.

5. Interpretation der Modellparameter

Ladungsmatrix sortieren und kleine Ladungen ausblenden

Der Output der EFA enthält zuerst die sogenannte Mustermatrix, welche die standardisierten Steigungsparameter \(\beta_{ziq}\) für jedes Item auf jeden Faktor zeigt.

Da die Mustermatrix oft unübersichtlich ist, sortieren und bereinigen wir die Darstellung. Dazu weisen wir das Ergebnis der Faktorenanalyse einem Objekt zu. Anstatt das Ergebnis direkt auszugeben, verwenden wir die print() Funktion:

fit_efa_extra <- fa(neo_extra, fm = "ml", rotate = "Promax", nfactors = 3, 
  scores = "Bartlett")

print(fit_efa_extra,
1  sort = TRUE,
2  cut = 0.15
)

1

sort = TRUE: Die Items werden nach absteigenden Ladungen sortiert, sodass die höchsten Ladungen oben stehen.

2

cut = 0.15: Ladungen kleiner als 0.15 werden ausgeblendet, um die Darstellung zu vereinfachen. (Das Argument für cut sollte reltaiv klein gewählt werden)

Output anzeigen

fit_efa_extra <- fa(neo_extra, fm = "ml", rotate = "Promax", nfactors = 3,
  scores = "Bartlett")
print(fit_efa_extra, sort = TRUE, cut = 0.15)

Factor Analysis using method =  ml
Call: fa(r = neo_extra, nfactors = 3, rotate = "Promax", scores = "Bartlett", 
    fm = "ml")
Standardized loadings (pattern matrix) based upon correlation matrix
    item   ML1   ML2   ML3   h2   u2 com
E8     8  0.92             0.77 0.23 1.0
E3     3  0.77             0.56 0.44 1.0
E9     9  0.70             0.48 0.52 1.0
E2     2  0.55             0.28 0.72 1.2
E7     7  0.39  0.28       0.28 0.72 2.0
E5     5        0.74       0.47 0.53 1.0
E10   10 -0.25  0.57       0.23 0.77 1.4
E11   11  0.30  0.39       0.31 0.69 1.9
E6     6       -0.20  0.80 0.46 0.54 1.2
E1     1        0.33  0.50 0.55 0.45 1.7
E4     4        0.19  0.42 0.39 0.61 1.6
E12   12        0.24  0.32 0.24 0.76 1.8

                       ML1  ML2  ML3
SS loadings           2.49 1.34 1.20
Proportion Var        0.21 0.11 0.10
Cumulative Var        0.21 0.32 0.42
Proportion Explained  0.49 0.27 0.24
Cumulative Proportion 0.49 0.76 1.00

 With factor correlations of 
     ML1  ML2  ML3
ML1 1.00 0.50 0.51
ML2 0.50 1.00 0.54
ML3 0.51 0.54 1.00

Mean item complexity =  1.4
Test of the hypothesis that 3 factors are sufficient.

df null model =  66  with the objective function =  3.23 with Chi Square =  1808.61
df of  the model are 33  and the objective function was  0.17 

The root mean square of the residuals (RMSR) is  0.03 
The df corrected root mean square of the residuals is  0.04 

The harmonic n.obs is  566 with the empirical chi square  70.96  with prob <  0.00014 
The total n.obs was  566  with Likelihood Chi Square =  92.37  with prob <  1.6e-07 

Tucker Lewis Index of factoring reliability =  0.932
RMSEA index =  0.056  and the 90 % confidence intervals are  0.043 0.07
BIC =  -116.8
Fit based upon off diagonal values = 0.99
Measures of factor score adequacy             
                                                   ML1  ML2  ML3
Correlation of (regression) scores with factors   0.94 0.85 0.85
Multiple R square of scores with factors          0.87 0.73 0.73
Minimum correlation of possible factor scores     0.75 0.46 0.45

Interpretation der Ladungsmatrix

• Spalte „Item“ gibt an, welches Item aus dem Datensatz analysiert wird.

• Spalten ML1, ML2, ML3 stehen für die drei extrahierten Faktoren. In den Spalten stehen die Schätzwerte für die standardisierten Steigungsparameter bzw. die Ladungen (\(\beta_{ziq}\)) der Items auf die Faktoren. Die Hauptladungen sollten stets positiv ausfallen, sofern alle Itemantworten im Datensatz richtig (d.h., in die gleiche Schlüsselrichtigung) kodiert sind. Ob negative Nebenladungen inhaltlich plausibel sind, hängt vom Inhalt des entsprechenden Items ab.

  Beispiel 1: Steigt der Wert auf Faktor ML1 um eine Standardabweichung und der Wert auf den anderen Faktoren bleibt konstant, dann erhöht sich die Antwort auf Item E8 im Mittel um 0.92 Standardabweichungen.

  Beispiel 2: Wenn sich Faktor ML1 um 1 SD erhöht und der Wert auf den anderen Faktoren konstant bleibt, sinkt die mittlere Itemantwort auf Item E10 im Mittel um 0.25 Standardabweichungen.

• Haupt- und Nebenladungen: Im Idealfall sollte jedes Item nur eine (deutlich von 0 unterschiedliche) Ladung auf einen Faktor haben. Diese Hauptladung sollte möglichst hoch sein, da dies bedeutet, dass die latente Variable durch dieses Item sehr gut abgebildet wird. Lädt ein Item auf mehr als einen Faktor (d.h., hat es eine oder mehrere Nebenladungen), ist die Einfachstruktur verletzt. Der Schweregrad der Verletzung hängt u.a. davon ab, wie hoch Haupt- und Nebenladungen ausfallen und ob die Faktoren dennoch inhaltlich interpretiert werden können.

  Beispiel 1: Item E7 lädt ähnlich hoch auf die Faktoren ML1 und ML2. Es weist damit eine Nebenladung auf und lässt sich nicht eindeutig zu einem Faktor zuordnen, da sich Haupt- und Nebenladung nicht stark unterscheiden. Außerdem hat das Item insgesamt eher niedrige Ladungen und wird scheinbar durch keinen der Faktoren besonders gut erklärt. Um dieses problematische Muster besser zu verstehen, sollte der Wortlaut des Items berücksichtigt werden (“Gefühl, vor Energie überzuschäumen”). Das Item könnte missverständlich formuliert sein (z.B. ist die Redewendung “vor Energie überschäumen” allgemein bekannt?) oder inhaltlich nicht zu den restlichen Items der drei Faktoren passen (siehe “Inhaltliche Interpretation”).

  Beispiel 2: Item E6 lädt ebenfalls auf zwei Faktoren. Allerdings unterscheiden sich seine Haupt- und Nebenladung deutlich in ihrer Höhe, sodass dieses Items recht eindeutig dem dritten Faktor zugeordnet werden kann. Dennoch verletzt es die Einfachstruktur und es sollte geprüft werden, ob sich in der Itemformulierung (“vorziehen Dinge alleine zu tun”) inhaltliche Gründe dafür finden.

• Inhaltliche Interpretation der Faktoren: Im Idealfall sollte jedes Item anhand seiner Hauptladung eindeutig zu einem der Faktoren zuordenbar sein. Für jeden Faktor können dann die zugehörigen Itemformulierungen inspiziert werden, um den Faktor inhaltlich zu interpretieren. Eine inhaltlich sinnvolle und zur Theorie passende Interpretation ist dabei jedoch nicht immer möglich. Achtung: Neben inhaltlichen Gründen können Faktoren auch strukturelle Ähnlichkeiten von Items abbilden (z.B. alle Items, die das Wort “nicht” enthalten, laden hoch auf einen Faktor).

  Beispiel 1: Dem ersten Faktor können die Items E8 (“ein fröhlicher Mensch”), E3 (“nicht besonders fröhlich”), E9 (“kein gut gelaunter Optimist”) und E2 (“leicht zum Lachen zu bringen”) anhand ihrer Hauptladungen eindeutig zugewiesen werden. All diesen Itemformulierungen ist gemein, dass sie eine positive Grundstimmung beschreiben, sodass der Faktor z.B. als Factette “Heiterkeit” interpretiert werden könnte.

  Beispiel 2: Dem dritten Faktor können die Items E6 (“vorziehen Dinge alleine zu tun”), E1 (“gerne viele Leute um sich”) und E4 (“gerne mit anderen unterhalten”) anhand ihrer Hauptladungen zugeordnet werden, obwohl sie jeweils eine gewisse Nebenladung aufweisen. Diese Items haben gemein, dass sie sich auf soziale Gesellschaft beziehen, sodass der Faktor z.B. als Facette “Geselligkeit” interpretiert werden könnte.

Weitere Interpretationen des Output

• Spalte h2 gibt die Kommunalität der Items an, also wie viel der Itemvarianz durch die extrahierten Faktoren erklärt wird. Dieser Wert dient als Reliabilitätsschätzung der einzelnen Items.

  Beispiel: Das Item E10 weist die niedrigste Kommunalität auf, d.h., es wird am schlechtesten durch die drei Faktoren zusammen erklärt.

• SS Loadings zeigt die Eigenwerte der drei Faktoren nach der Rotation, also wie gut die Faktoren die Items jeweils erklären.

  Beispiel: Der Faktor 1 weist den höchsten Eigenwert auf, d.h., er ist am besten im Stand die Itemantworten zu erklären.

• Factor Correlations: Unten im Output finden Sie die geschätzten Korrelationen zwischen den Faktoren. Diese werden nur bei obliquer Rotationstechnik geschätzt.

  Beispiel: Die Faktoren ML1 und ML2 korrelieren mit 0.5, d.h. je höher die Ausprägung einer Person auf dem Faktor ML1, desto höher im Mittel auch die Ausprägung auf dem Faktor ML2.

6. Nächste Schritte

Wenn die Faktorlösung der EFA zufriedenstellend ausgefallen ist (d.h., gut interpetierbar ist), sollte das gefundene Modell erneut im Rahmen einer CFA geschätzt werden, um seine Modellpassung zu evaluieren. Idealerweise wird die CFA sogar mit einer neuen Stichprobe durchgeführt. Wird die CFA auf dem gleichen Datensatz durchgeführt als die EFA, stellt dies keinen sehr strengen Test für das basierend auf den Ergebnissen der EFA spezifizierte Testmodell dar. Hat man sich schließlich auf ein finales Testmodell geeinigt, sollten weitere Gütekriterien des Tests wie Reliabilität oder Validität untersucht werden.

Wenn die Faktorlösung der EFA nicht zufriedenstellend war, gibt es mehrere Optionen für das weitere Vorgehen:

Rotationsmethoden vergleichen: Promax vs. Oblimin

Eine Möglichkeit wäre es, die Rotation zu ändern. Hierzu können Sie im fa() Befehl rotate = "Promax" z.B. durch rotate = "oblimin" ersetzen. Beide sind oblique Rotationsmethoden (d. h., die Faktoren dürfen korrelieren). Der Code dafür:

fit_efa_extra <- fa(neo_extra, fm = "ml", rotate = "oblimin", nfactors = 3, scores = "Bartlett")
print(fit_efa_extra, sort = TRUE, cut = 0.15)

Output anzeigen

fit_efa_extra <- fa(neo_extra, fm = "ml", rotate = "oblimin", nfactors = 3, scores = "Bartlett")

Loading required namespace: GPArotation

print(fit_efa_extra, sort = TRUE, cut = 0.15)

Factor Analysis using method =  ml
Call: fa(r = neo_extra, nfactors = 3, rotate = "oblimin", scores = "Bartlett", 
    fm = "ml")
Standardized loadings (pattern matrix) based upon correlation matrix
    item   ML1   ML2   ML3   h2   u2 com
E8     8  0.89             0.77 0.23 1.0
E3     3  0.74             0.56 0.44 1.0
E9     9  0.68             0.48 0.52 1.0
E2     2  0.53             0.28 0.72 1.1
E7     7  0.40  0.26       0.28 0.72 1.8
E5     5        0.67       0.47 0.53 1.0
E10   10 -0.18  0.51       0.23 0.77 1.3
E11   11  0.33  0.36       0.31 0.69 2.0
E6     6              0.72 0.46 0.54 1.1
E1     1        0.35  0.49 0.55 0.45 1.9
E4     4  0.18  0.22  0.41 0.39 0.61 1.9
E12   12        0.25  0.32 0.24 0.76 2.0

                       ML1  ML2  ML3
SS loadings           2.55 1.31 1.18
Proportion Var        0.21 0.11 0.10
Cumulative Var        0.21 0.32 0.42
Proportion Explained  0.51 0.26 0.23
Cumulative Proportion 0.51 0.77 1.00

 With factor correlations of 
     ML1  ML2  ML3
ML1 1.00 0.34 0.39
ML2 0.34 1.00 0.33
ML3 0.39 0.33 1.00

Mean item complexity =  1.4
Test of the hypothesis that 3 factors are sufficient.

df null model =  66  with the objective function =  3.23 with Chi Square =  1808.61
df of  the model are 33  and the objective function was  0.17 

The root mean square of the residuals (RMSR) is  0.03 
The df corrected root mean square of the residuals is  0.04 

The harmonic n.obs is  566 with the empirical chi square  70.96  with prob <  0.00014 
The total n.obs was  566  with Likelihood Chi Square =  92.37  with prob <  1.6e-07 

Tucker Lewis Index of factoring reliability =  0.932
RMSEA index =  0.056  and the 90 % confidence intervals are  0.043 0.07
BIC =  -116.8
Fit based upon off diagonal values = 0.99
Measures of factor score adequacy             
                                                   ML1  ML2  ML3
Correlation of (regression) scores with factors   0.93 0.83 0.83
Multiple R square of scores with factors          0.87 0.68 0.68
Minimum correlation of possible factor scores     0.74 0.36 0.37

Was ändert sich (in unserem Beispiel)?

• Die Grundstruktur bleibt ähnlich.
• Unterschiede:
  • Die spezifischen Ladungen einzelner Items können sich leicht ändern.
  • Die Korrelationen zwischen den Faktoren fallen bei „oblimin“ oft geringer aus.

Anzahl der Faktoren anpassen

Manchmal kann eine starke Abweichung von der Einfachstruktur behoben oder verbessert werden, wenn man die Anzahl der Faktoren reduziert (z.B. wenn ein Faktor keine Hauptladungen aufweist) oder erweitert (z.B. wenn einzelne Items auf keinem Faktor hoch laden). Hierzu können Sie im fa() Befehl die Anzahl der Faktoren nfactors = 3 anpassen und die Mustermatrix erneut analysieren.

Items entfernen

Wenn sich einzelne Items als problematisch erwiesen haben (z.B. durch hohe Nebenladungen; generell niedrige Ladungen) besteht die Möglichkeit, diese probehalber zu entfernen und die EFA erneut zu schätzen. Falls die Mustermatrix nach dieser Anpassung besser interpretierbar ist, kann darüber nachgedacht werden das Item dauerhaft zu entfernen oder umzuformulieren.

Aber Achtung: Ein Item darf nur dann entfernt werden, wenn es inhaltlich redundant ist und somit nicht für die Inhaltsvalidität benötigt wird. Ansonsten müssen die zugrundeliegende Konstruktdefinition und Theorie angepasst werden.

Theorie revidieren

Falls keine zufriedenstellende Faktorlösung gefunden werden kann oder die gefundene Faktorlösung inhaltlich nicht sinnvoll ist, muss ggf. die zugrundeliegende Theorie verworfen oder angepasst werden.

3 Arbeitsauftrag

Wiederholen Sie die Analysen aus dem Video mit der Skala Gewissenhaftigkeit (Variablennamen: C1, C2, … , C12) des Beispieldatensatzes (NEO_original.csv):

• Führen Sie eine Parallelanalyse im Rahmen einer exploratorischen Faktorenanalyse mit Maximum Likelihood Schätzung durch.
• Führen Sie für die resultierende Anzahl an Faktoren eine exploratorische Faktorenanalyse mit Maximum Likelihood Schätzung und Oblimin oder Promax Rotation durch.
• Schauen Sie sich die resultierenden Parameterschätzungen für das mehrdimensionale \(\tau\)-kongenerische Messmodell an.

Lösung

## Beispieldatensatz laden
neo <- read.csv("NEO_original.csv")

## Vektor mit Namen der gewünschten Spalten
gewiss_items <- c("C1", "C2", "C3", "C4", "C5", "C6", 
                  "C7", "C8", "C9", "C10", "C11", "C12")
neo_gewiss <- neo[, gewiss_items]

## EFA
# Parallelanalyse um Faktorenzahl zu bestimmen:
fa.parallel(neo_gewiss, 
            fm = "ml", 
            fa = "fa", 
            quant = 0.95, 
            n.iter = 1000)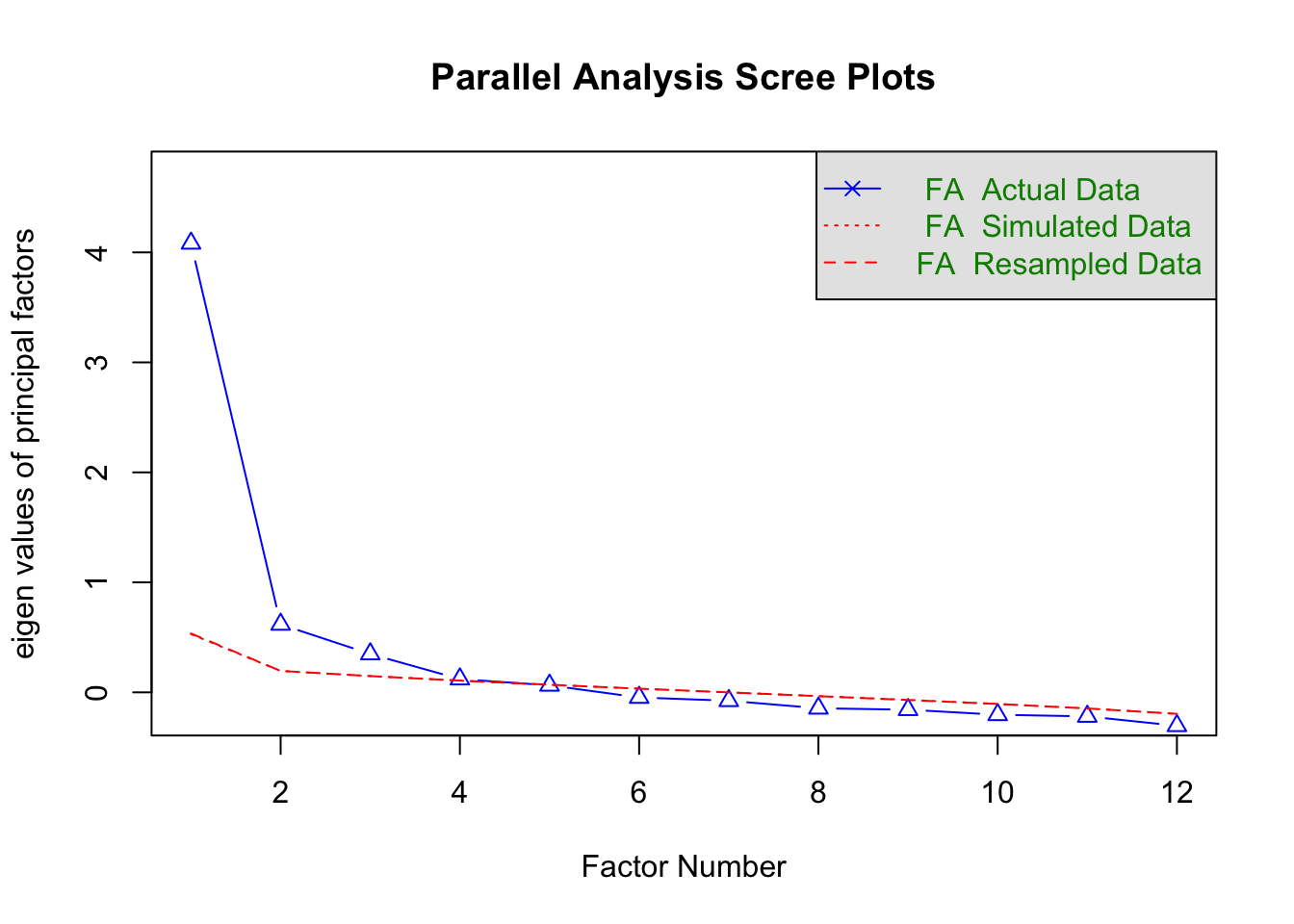

Parallel analysis suggests that the number of factors =  3  and the number of components =  NA 

# Faktorenanalyse für Gewissenhaftigkeit
fit_efa_gewiss <- fa(neo_gewiss, 
                     nfactors = 3, 
                     fm = "ml", 
                     rotate = "oblimin", 
                     scores = "Bartlett")

# sortierte Ladungsmatrix mit kleinen Ladungen ausgeblendet
print(fit_efa_gewiss, cut = 0.15, sort = TRUE)

Factor Analysis using method =  ml
Call: fa(r = neo_gewiss, nfactors = 3, rotate = "oblimin", scores = "Bartlett", 
    fm = "ml")
Standardized loadings (pattern matrix) based upon correlation matrix
    item   ML1   ML2   ML3   h2   u2 com
C2     2  0.76             0.57 0.43 1.0
C11   11  0.68             0.48 0.52 1.0
C6     6  0.59             0.43 0.57 1.1
C1     1  0.53             0.34 0.66 1.1
C3     3  0.41             0.24 0.76 1.2
C7     7        0.81       0.67 0.33 1.0
C12   12        0.56       0.31 0.69 1.2
C5     5  0.37  0.53       0.54 0.46 1.9
C10   10  0.21  0.39  0.29 0.52 0.48 2.5
C8     8              0.74 0.56 0.44 1.0
C4     4        0.29  0.47 0.41 0.59 1.7
C9     9  0.35        0.44 0.44 0.56 1.9

                       ML1  ML2  ML3
SS loadings           2.42 1.76 1.32
Proportion Var        0.20 0.15 0.11
Cumulative Var        0.20 0.35 0.46
Proportion Explained  0.44 0.32 0.24
Cumulative Proportion 0.44 0.76 1.00

 With factor correlations of 
     ML1  ML2  ML3
ML1 1.00 0.51 0.47
ML2 0.51 1.00 0.45
ML3 0.47 0.45 1.00

Mean item complexity =  1.4
Test of the hypothesis that 3 factors are sufficient.

df null model =  66  with the objective function =  3.84 with Chi Square =  2152.16
df of  the model are 33  and the objective function was  0.18 

The root mean square of the residuals (RMSR) is  0.03 
The df corrected root mean square of the residuals is  0.04 

The harmonic n.obs is  566 with the empirical chi square  66.5  with prob <  0.00049 
The total n.obs was  566  with Likelihood Chi Square =  98.52  with prob <  1.9e-08 

Tucker Lewis Index of factoring reliability =  0.937
RMSEA index =  0.059  and the 90 % confidence intervals are  0.046 0.073
BIC =  -110.65
Fit based upon off diagonal values = 0.99
Measures of factor score adequacy             
                                                   ML1  ML2  ML3
Correlation of (regression) scores with factors   0.91 0.89 0.85
Multiple R square of scores with factors          0.82 0.80 0.72
Minimum correlation of possible factor scores     0.64 0.60 0.44

Kurze Zusammenfassung:

• Die Parallelanalyse schlägt für die Gewissenhaftigkeitsitems drei Faktoren vor.
• In der Mustermatrix auffällig sind die Items C5, C10, C4 und C9, da sie Nebenladungen aufweisen und damit die Einfachstruktur verletzen. Insbesondere die Items C10 und C9 sind dabei kritisch, da sie ähnlich hohe Haupt- und Nebenladungen aufweisen und keinem Faktor eindeutig zugeordnet werden können, wobei Item C10 zudem recht niedrig über alle Faktoren lädt. Ggf. könnte der Wortlaut des Items dafür verantwortlich sein (“tüchtige Person, die ihre Arbeit immer erledigt”), da es zwei Inhalte abfragt (“tüchtig” und “Arbeit immer erledigt”).
• Die niedrigste Kommunalität hat Item C3 (“kein sehr systematisch vorgehender Mensch”)
• Die drei Faktoren korrelieren untereinander positiv und mit ähnlicher (mittlerer) Höhe.
• Für die Interpretation der verschiedenen Modellparameter orientieren Sie sich bitte am Beispiel der Extraversionsskala.