library(lavaan)
library(psych)
library(MBESS)
library(corrplot)Arbeitsauftrag: Reliabilität und Validität
1 Einführung
In diesem Tutorial werden Sie darauf vorbereitet, wie Sie die Daten aus Ihrem im UK erstellten Fragebogen hinsichtlich Reliabilität und Validität in R auswerten können. Dazu arbeiten wir zunächst wieder mit demselben Beispieldatensatz wie in den beiden bisherigen Arbeitsauträgen. Es werden neben neuen Techniken auch die Verfahren der CFA und EFA verwendet, die Sie in den beiden vorherigen Arbeitsaufträgen kennen gelernt haben.
Wir werden die Analysen zur Reliabilität und Validität zunächst einmal gemeinsam durcharbeiten, bevor Sie den vollständigen Ablauf dann eigenständig im Arbeitsauftrag anwenden.
1.1 Vorbereitung in R
Bitte führen Sie nun folgende Schritte aus, um unser Skript für die Analyse vorzubereiten:
Legen Sie ein neues R-Skript an und speichern Sie es in dem Ordner, in dem Ihr RStudio Projekt liegt, z. B. unter dem Namen Rel_und_Val ab.
Laden Sie die Pakete, die wir für die Analysen benötigen
Hinweis: Stellen Sie sicher, dass alle Pakete bereits installiert sind. Falls nicht, können Sie dies mit
install.packages("paketname")nachholen.Laden Sie den Datensatz
neo <- read.csv("NEO_original.csv")
1.2 Geschlecht numerisch kodieren
Wir verwenden in unserem Anwendungsbeispiel weiter unten das Geschlecht als Kriteriumsvariable (aus Mangel an besseren Alternativen) und müssen es dafür in eine Dummy-Variable umkodieren. Frauen werden dabei mit 1 und Männer mit 0 kodiert. Durch diese Kodierung wird das Geschlecht zu einer numerischen Variable, mit der wir rechnen können.
Aktuell ist die Variable Sex im Datensatz als Text (character oder string) gespeichert, hier konkret mit den Werten "female" und "male". Um die Dummy-Kodierung vorzunehmen, ersetzen wir diese Textwerte durch die Werte 1 und 0 (wir überschreiben also die ursprüngliche Variable). Anschließend wandeln wir die Variable explizit in einen numerischen Datentyp um.
# Text-Kodierung durch Dummy-Kodierung ersetzen
neo[neo$Sex == "female", "Sex"] <- 1
neo[neo$Sex == "male", "Sex"] <- 0
# Character Variable in numerische Variable umwandeln
neo$Sex <- as.numeric(neo$Sex)Erklärung des Codes:
- Zeilen auswählen und überschreiben:
neo$Sex == "female": Dieser Vergleich prüft, ob der Wert in der Spalte"Sex"gleich"female"ist. Das Ergebnis ist ein logischer Vektor (TRUE/FALSE).neo[neo$Sex == "female", "Sex"] <- 1: Alle Zeilen, bei denen der Vergleich zu TRUE evaluiert wird, werden mit 1 überschrieben.- Analog dazu wird
"male"durch 0 ersetzt.
- Umwandlung in numerischen Typ:
- Nach dem Überschreiben ist die Variable „Sex“ technisch gesehen immer noch ein String (also “1” und “0” als Text).
- Mit
neo$Sex <- as.numeric(neo$Sex)wandeln wir die gesamte Spalte in echte Zahlenwerte um (0 und 1).
Hinweis: Sie können die Variable neo$Sex anschauen, um sicherzugehen, dass die Kodierung korrekt ist.
1.3 Vektor mit den Itemnamen der Skalen erstellen
Für unsere Analysen benötigen wir zwei Skalen aus dem NEO-Datensatz: Extraversion und Neurotizismus. Damit wir die entsprechenden Items nicht jedes Mal händisch auswählen müssen, erstellen wir zwei Vektoren, die die Namen der Items der entsprechenden Skala enthalten:
extra_items <- c("E1", "E2", "E3", "E4", "E5", "E6",
"E7", "E8", "E9", "E10", "E11", "E12")
neuro_items <- c("N1", "N2", "N3", "N4", "N5", "N6",
"N7", "N8", "N9", "N10", "N11", "N12")1.4 Summenwerte der Skalen berechnen
Bevor wir Summenwerte für Skalen berechnen, müssen wir uns sicher sein, dass alle Items richtig herum gepolt sind (d.h. dass höhere Werte in der Variable im Datensatz immer für höhere Werte auf der zugrunde liegenden latenten Variable sprechen). In unserem Beispieldatensatz NEO_original.csv wurden bereits von der Umfragesoftware alle notwendigen Items umkodiert, sodass dieser Schritt hier wegfällt. Für den Datensatz mit Ihrem eigenen Fragebogen aus dem UK ist aber eventuell eine Umkodierung für einzelne Items notwendig.
Beispiel: Wir erstellen einen simulierten data.frame d, in dem 10 Personen ein 5-stufiges Impulsivitätsitem d$I1 (Ich denke zuerst nach, bevor ich handle) beantwortet haben. Das Item ist kodiert von 1-5 (1: trifft gar nicht zu, …, 5: trifft voll und ganz zu), wobei hier niedrige Werte in der Itemantwort für höhere Werte auf der latenten Variable Impulsivität sprechen.
d <- data.frame(I1 = sample(c(1:5), size = 10, replace = TRUE))
d$I1 [1] 2 2 1 5 2 5 5 1 5 4Eine einfache Methode, das Item umzukodieren (1 -> 5, 2 -> 4, 3 -> 3, 4 -> 2, 5 -> 1), ist der folgende mathematische Trick:
d$I1_r <- 6 - d$I1
d$I1_r [1] 4 4 5 1 4 1 1 5 1 2Es bleibt Ihnen überlassen, ob Sie die ursprüngliche Variable d$I1 überschreiben (d$I1 <- 6 - d$I1) oder lieber eine neue Variable (d$I1_r <- 6 - d$I1) erstellen. Der Vorteil von Überschreiben ist, dass Sie sich nicht merken müssen, welche Variablen umkodiert wurden, wenn Sie für spätere Analysen Items aus dem Datensatz auswählen wollen. Der Nachteil von Überschreiben ist, dass wenn Sie den Code aus Versehen 2 mal hintereinander ausführen, die Variable wieder zurück kodiert wird und damit folgende Analysen ein falsches Ergebnis liefern.
Um später die Reliabilität und Validität der Skalen Extraversion und Neurotizismus zu analysieren, berechnen wir zunächst die Summenwerte (Skalenwerte) für jede Person. Dazu verwenden wir die Funktion rowSums(), die in einem data.frame für jede Zeile die Summe der Werte über alle Spalten berechnet.
neo$E_sum <- rowSums(neo[, extra_items])
neo$N_sum <- rowSums(neo[, neuro_items])Erklärung des Codes:
- Neue Variablen erstellen:
neo$E_sum: Erstellt eine neue Variable mit Namen “E_sum” im Datensatz, die die Summenwerte der Extraversionsitems speichert.neo$N_sum: Erstellt eine analoge Variable für die Neurotizismusitems.
- Auswahl der Spalten:
- Mit
neo[, extra_items]werden alle Zeilen der Spalten ausgewählt, die im Vektor extra_items definiert sind. - Das Gleiche gilt für
neuro_items.
- Mit
- Summen berechnen:
rowSums()berechnet für jede Zeile (jede Person) die Summe der ausgewählten Spalten (der extra_items bzw. neuro_items). Das Ergebnis ist ein Vektor mit Summenwerten, der in den neuen Variablen gespeichert wird.
Falls Sie die berechneten Summenwerte ansehen möchten, können Sie den folgenden Code ausführen:
head(neo$E_sum) # Zeigt die ersten Zeilen der Summenwerte für Extraversion
head(neo$N_sum) # Zeigt die ersten Zeilen der Summenwerte für Neurotizismushead(neo$E_sum) # Zeigt die ersten Zeilen der Summenwerte für Extraversion[1] 24 12 28 20 22 22head(neo$N_sum) # Zeigt die ersten Zeilen der Summenwerte für Neurotizismus[1] 34 9 30 21 35 36Hinweis: Als Skalenwert könnte man statt dem Summenwert ebenso gut den Mittelwert der Items pro Skala berechnen. Die nachfolgenden Schritte zur Prüfung der Reliabilität und Validität würden dann analog ablaufen.
2 Reliabilität
Ein psychologischer Test, bzw. der im Rahmen eines solchen Tests berechnete Testscore (z.B. der Summenwert einer Skala), gilt als reliabel, wenn die Testergebnisse genau, d.h. wenig fehlerbehaftet sind. Die Reliabilität gibt an, welcher Anteil der Varianz im Testscore durch die im Testmodell spezifizierte latente Variable (das Konstrukt) erklärt wird.
Nachdem wir die Summenwerte für die Skalen Extraversion und Neurotizismus berechnet haben, können wir jetzt die Reliabilität dieser Skalen schätzen. Wir verwenden hierzu die beiden Maße Cronbachs Alpha und McDonalds Omega.
# Reliabilität der Skala Extraversion
alpha_extra <- ci.reliability(neo[, extra_items], type = "alpha",
interval.type = "ml")
omega_extra <- ci.reliability(neo[, extra_items], type = "omega",
interval.type = "ml")
# Reliabilität der Skala Neurotizismus
alpha_neuro <- ci.reliability(neo[, neuro_items], type = "alpha",
interval.type = "ml")
omega_neuro <- ci.reliability(neo[, neuro_items], type = "omega",
interval.type = "ml")Erklärung des Codes:
ci.reliability: Diese Funktion stammt aus dem Paket MBESS und berechnet verschiedene Arten von Reliabilität.neo[, extra_items]: Die Spalten des Datensatzes, die die entsprechenden Items enthalten. Wir möchten die Reliabilität jeweils nur über die Items einer Skala bestimmen.type: Gibt an, welche Reliabilitätsart berechnet werden soll"alpha": Cronbachs Alpha"omega": McDonalds Omega
interval.type: Gibt an, wie das Konfidenzintervall geschätzt wird (hier: “ml” für Maximum Likelihood).
Ausgabe verstehen:
Am Beispiel von Cronbachs Alpha der Extraversionsskala:
alpha_extra$est
[1] 0.7974403
$se
[1] 0.01221146
$ci.lower
[1] 0.7735063
$ci.upper
[1] 0.8213743
$conf.level
[1] 0.95
$type
[1] "alpha"
$interval.type
[1] "maximum likelihood (wald ci)"est: Der Punktschätzer, also der geschätzte Wert für die Reliabilität (hier \(\alpha = 0.79\)). Das heißt 79% der Unterschiede im Extraversionssummenwert können auf die latente Variable Extraversion zurückgeführt werden. Die restlichen 21% sind Fehlervarianz.se: Der Standardfehler der Schätzung.- Ein 95%-Konfidenzintervall, das die Unsicherheit der Schätzung angibt: [0.77, 0.82]. Das Intervall basiert auf Maximum-Likelihood-Schätzungen und wird in der Ausgabe als wald ci bezeichnet.
Die Reliabilitätsschätzung der Neurotizismusskala kann analog betrachtet und interpretiert werden. Für die Neurotizismusskala erhalten wir einen höheren Punktschätzer und höhere Konfidenzintervalle als für die Extraversionsskala.
Für die Beurteilung der Reliabilität gibt es keine allgemein anerkannten Cut-Off Werte. Häufig werden Werte ab 0.70 als akzeptabel und ab .80 als gut betrachtet.
Eindimensionalität:
Die hier durchgeführte Schätzung der Reliabilität setzt voraus, dass die Skala eindimensional ist, also mindestens das eindimensionale \(\tau\)-kongenerische Modell gilt. Bei unserer Extraversionsskala wissen wir bereits, dass sie vermutlich nicht eindimensional ist (siehe Parallelanalyse im Arbeitsauftrag zur EFA). Trotzdem berechnen wir Cronbachs Alpha und McDonalds Omega, um die Methode zu demonstrieren.
McDonalds Omega vs. Cronbachs Alpha:
Omega ist eine bessere Schätzung der Reliabilität, da es auf dem \(\tau\)-kongenerischen Modell basiert, das weniger strenge Annahmen über die Daten macht. Cronbachs Alpha stellt nur eine optimale Relibilitätsschätzung dar, wenn mindestens das essentiell \(\tau\)-äquivalente Modell gilt. Wenn ein weniger strenges Modell gilt, stellt Cronbachs Alpha nur eine Mindestschätzung der Reliabilität dar. Aus diesem Grund fällt die Reliabilitätsschätzung mit Omega in der Regel höher aus als mit Alpha.
3 Validität
Die Validität stellt das wichtigste Gütekriterium für jeden psychologischen Test dar. Wir werden uns gleich die verschiedenen Arten von Validität im Detail anschauen. Für diese durchaus komplexen Analysen wird immer die Gültigkeit eines Testmodells (in der Regel das \(\tau\)-kongenerische Modell) vorausgesetzt. Gleichzeitig müssen wir jedoch in der Praxis immer davon ausgehen, dass keines unserer Testmodelle gilt (was wir auch für unseren Beispieldatensatz bereits im Kapitel zur CFA gesehen haben). Es ist daher für die Verwendung psychologischer Tests in der Praxis eine sehr komplizierte (und teilweise ungelöste) Frage, unter welchen Bedinungen eine modellbasierte Auswertung gerechtfertigt ist und wir können dieses Problem hier nicht lösen. Wir wollen Ihnen daher zu Beginn auch eine stark vereinfachte Auswertung zeigen, die auf Korrelationsanalysen basiert. Eine solche Analyse ist besonders einfach durchzuführen und zu interpretieren. Gleichzeitig verdeutlicht eine solche Analyse besonders gut die intuitive Grundidee der Validierung eines Tests, ohne sich in den technischen Details der ausführlicheren Analysen zu verlieren.
3.1 Vereinfachte Auswertung zur Validität mit Korrelationsanalysen
Im Rahmen der Konstruktdefinition haben wir über das nomologische Netzwerk gesprochen, das theoretisch angenommene Beziehungsgeflecht zwischen den Konstrukten des Tests und anderen Konstrukten oder “messfehlerfreien” Variablen.
Die einfachste Analyse, die Hinweise darüber liefern kann, inwiefern die im nomologischen Netz festgelegten theoretischen Annahmen zutreffen, ist eine Betrachtung der Korrelationen zwischen den Summenwerten aller Facetten des zu untersuchenden Konstrukts untereinander, sowie zwischen den Summenwerten des Konstrukts und den Summenwerte anderer Konstrukte, und messfehlerfreien Kriteriumsvariablen.
Natürlich ist eine solche Analyse nicht perfekt (z.B. wird die Reliabilität der Summenwerte ignoriert, siehe Minderungskorrektur; psychologische Testmodelle werden nicht überprüft; der Schätzfehler in den Punktschätzern der Korrelationen wird ignoriert), jedoch ist eine solche deskriptive Analyse in der Praxis trotzdem sehr hilfreich und sollte auf keinen Fall übersprungen werden.
Wir betrachten deshalb die Korrelationen auf Ebene der Skalenwerte:
- 1
-
Berechnen der Korrelationsmatrix für einen Teildatensatz, der nur die Skalenwerte, sowie die beiden messfehlerfreien Kriterien Geschlecht und Alter enthält, mit der Funktion
cor(). Es werden per Default Pearsonkorrelationen berechnet. Alternativ könnten statt den Pearsonkorrelationen mitmethod = "spearman"auch Rangkorrelationen verwendet werden. - 2
-
Die Funktion
corrplot()aus dem Paket corrplot erstellt eine grafische Darstellung der Korrelationsmatrix. Das ist nicht unbedingt notwendig (man könnte auch direkt cor_mat betrachten), aber besonders für die Interpretation großer Korrelationmatrizen sehr hilfreich. Mit dem Argumentmethodsind verschiedene Darstellungsoptionen möglich (siehe?corrplot).
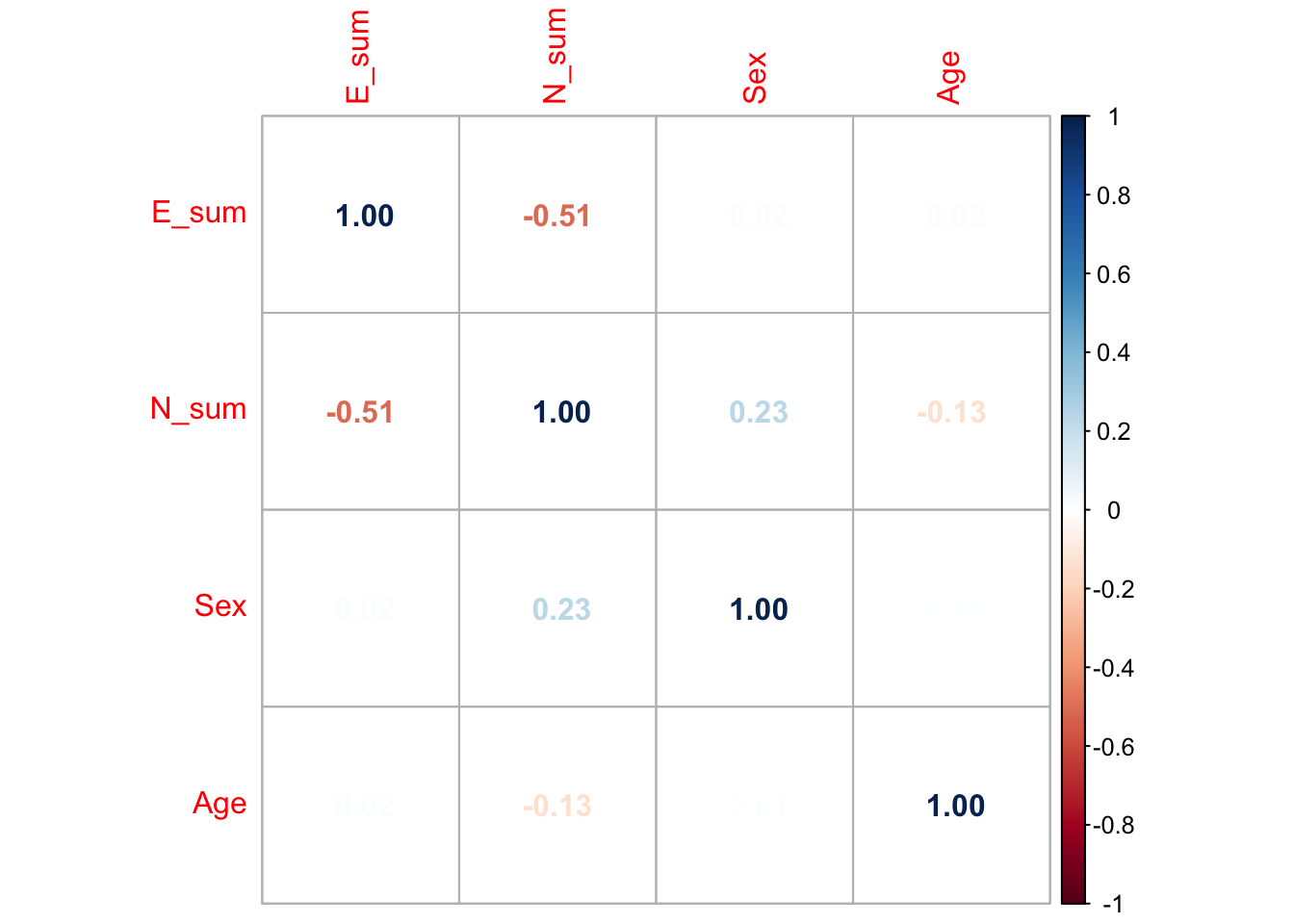
Faktorielle Validität: Zusammenhänge der Konstrukte innerhalb eines Fragebogens wie theoretisch erwartet.
Beispiel: Angenommen, wir untersuchen ein Konstrukt “Big 2 - Persönlichkeit”, das aus den beiden Facetten Extraversion und Neurotizismus besteht. Dann kann die beobachtete Korrelation zwischen den Summenwerten der Extraversions- und Neurotizismusitems im Sinne der faktoriellen Validität mit dem theoretisch angenommenen Zusammenhang zwischen den Facetten verglichen werden. Wäre die Theorie z.B. von einem negativen Zusammenhang der Big 2 ausgegangen, würde die oben abgebildete Korrelation der Skalenwerte E_sum und N_sum für die faktorielle Validität sprechen.
Die faktorielle Validität ist nahe verwandt mit dem Gütekriterium der Skalierung, also ob für die zur Messung des Konstrukts verwendeten Items ein psychologische Testmodell gilt. Eine Korrelationsanalyse kann zwar nicht prüfen, ob eine Skala aus mehreren Items eindimensional ist. Jedoch können die Korrelationen zwischen den Items einer Skala durchaus Hinweise liefern, die dagegen sprechen, dass alle Items das gleiche Konstrukt messen.
Beispiel: Würden im vorliegenden Beispiel zwei Items der Skala Extraversion nahezu gar nicht oder substantiell negativ korrelieren, wäre dies nicht mit der Konstruktdefinition kompatibel. Um dies zu prüfen, können wie die Korrelationen der Extraversions-Items untereinander betrachten:
cor_mat <- cor(neo[, extra_items])
corrplot(cor_mat, method = "number")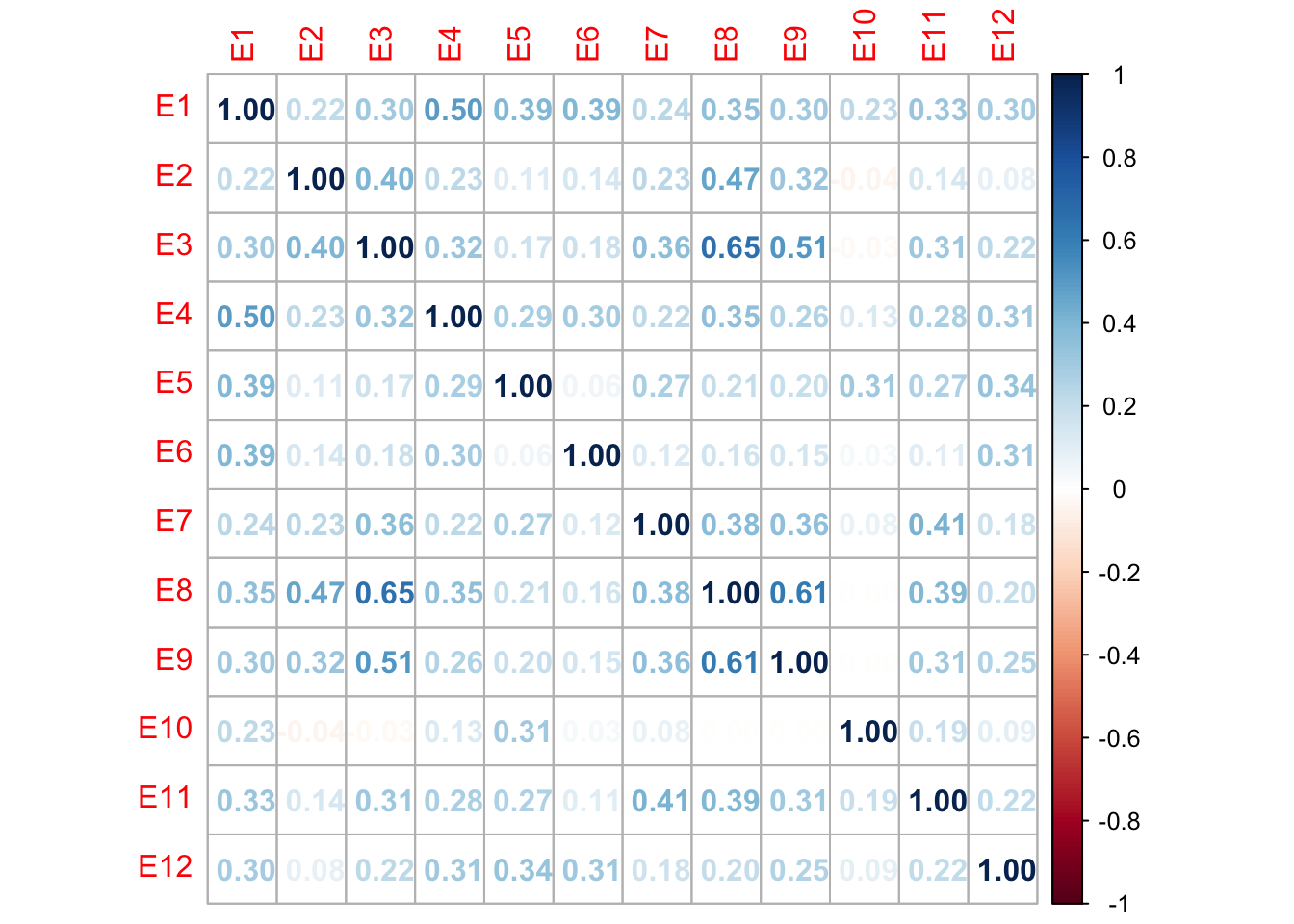
Auch wenn wir keine substantiell negativen Korrelationen beobachten, gibt es jedoch einige Items, die fast gar nicht miteinander korrelieren, z.B. die Items E9 und E10.
Divergente (bzw. konvergente) Validität: Zusammenhänge mit Fragebögen zu anderen Konstrukten (bzw. zum gleichen Konstrukt) wie theoretisch erwartet.
Beispiel: Angenommen, wir untersuchen das Konstrukt Extraversion und erheben zusätzlich das Konstrukt Neurotizismus. Dann kann die beobachtete Korrelation zwischen den Summenwerten der Extraversions- und Neurotizismusitems im Sinne der divergenten Validität mit dem theoretisch angenommenen Zusammenhang zwischen den Konstrukten Extraversion und Neurotizismus verglichen werden. Wäre die Theorie z.B. von einem negativen Zusammenhang der beiden Konstrukte ausgegangen, würde die oben abgebildete Korrelation der Skalenwerte E_sum und N_sum für die divergente Konstruktvalidität sprechen.
Kriteriumsvalidität: Zusammenhänge mit einem “messfehlerfreien” Kriterium wie theoretisch erwartet.
Beispiel: Angenommen, wir untersuchen das Konstrukt Neurotizismus und erheben zusätzlich die Kriterien Alter und Geschlecht. Dann kann die beobachtete Korrelation zwischen dem Summenwert der Neurotizismusskala und den Variablen Alter und Geschlecht im Sinne der Kriteriumsvalidität mit dem theoretisch angenommenen Zusammenhang zwischen dem Konstrukt Neurotizismus und den beiden Kriterien verglichen werden. Wäre die Theorie z.B. von einem positiven Zusammenhang zwischen Neurotizismus und Geschlecht ausgegangen (d.h., Frauen haben höhere Neurotiszimuswerte), würde die Korrelation des Skalenwerts N_sum mit der Variable Age für die Kriteriumsvalidität sprechen.
Alternativ zur Betrachtung der Korrelation könnten wir auch ein Konfidenzintervall für den Mittelwertsunterschied im Summenwert zwischen den Geschlechtern berechnen. Damit hätten wir nicht nur einen Punktschätzer sondern können den Schätzfehler mit berücksichtigen:
t.test(N_sum ~ Sex, data = neo)
Welch Two Sample t-test
data: N_sum by Sex
t = -5.6018, df = 373.67, p-value = 4.12e-08
alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0
95 percent confidence interval:
-5.942389 -2.854518
sample estimates:
mean in group 0 mean in group 1
20.21693 24.61538 Ergebnisse:
- Mittelwert Männer (Sex = 0): 20.22
- Mittelwert Frauen (Sex = 1): 24.62
- Das 95%-Konfidenzintervall für die Differenz zwischen den Mittelwerten beträgt [-5.94; -2.85].
Hinweis: Es ist bekannt, dass Frauen höhere Neurotizismuswerte haben als Männer, wir können das Ergebnis unseres t-Tests somit als Validitätshinweis nutzen.
Die Interpretation der Korrelation zwischen dem Summenwert der Skala und den Kriteriumsvariablen nimmt implizit an, dass die Skala eindimensional ist. Wäre die Skala wirklich eindimensional, ist es nicht notwendig, die Korrelation einzelner Items mit dem Kriterium zu betrachten. Da wir aber immer davon ausgehen müssen, dass unsere Skalen niemals perfekt eindimensional sind, ist es durchaus sinnvoll, auch immer die einzelnen Korrelationen auf Itemebene zu betrachten und diese hinsichtlich der Plausibilität der Konstruktdefinition zu prüfen.
Beispiel: Würden sich im vorliegenden Beispiel die Korrelationen der Neurotizismusitems mit dem Kriterium Geschlecht stark unterscheiden, vielleicht sogar im Vorzeichen, wäre dies vermutlich nicht mit der Konstruktdefinition von Neurotizismus oder dem nomologischen Netzwerk kompatibel:
cor_mat <- cor(neo[, c(neuro_items, "Sex", "Age")])
corrplot(cor_mat, method = "number")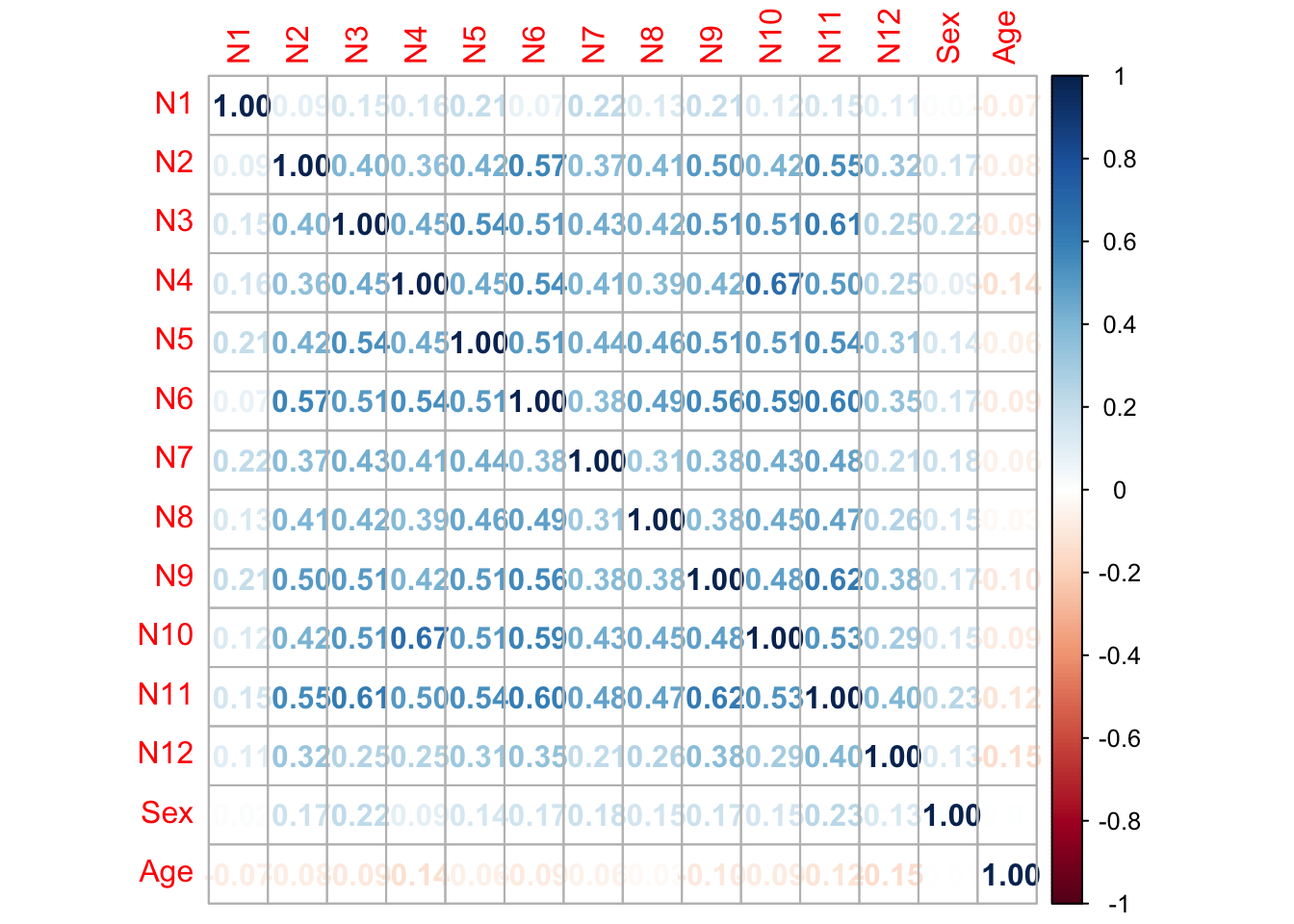
Grundsätzlich sind die Korrelationen aller Items mit dem Kriterium Geschlecht im Betrag eher niedrig. Der Datensatz ist jedoch sehr groß, sodass die höchsten Korrelationen durchaus signifikant von 0 verschieden sind (siehe z.B. die Funktion cor.test()). Es zeigt sich, dass alle Neurotizismusitems positiv mit Sex korrelieren, wenn auch z.B. das Item N1 sehr schwach. Diese Beochbachtung ist mit der Eindimensionalität der Neurotiszimusitems einigermaßen gut vereinbar.
Nachdem wir uns mit den Korelationsanalysen einen ersten intuitiven Eindruck verschafft haben, werden wir im Folgenden die einzelnen Validitätsarten noch einmal mit den komplexeren, modellbasierten Analysen untersuchen.
3.2 Konstruktvalidität
Ein wichtiger Aspekt der Konstruktvalidität ist die faktorielle Validität, also die Frage, ob die gemessenen Items tatsächlich die zugrunde liegenden latenten Faktoren abbilden und ob die Faktorstruktur den theoretischen Annahmen entspricht. Diese Frage ist eng verwandt mit der Frage nach der Skalierbarkeit und wir verwenden dafür eine Konfirmatorische Faktorenanalyse (CFA).
3.2.1 CFA: Faktorielle Validität
Unsere Konstruktdefinition und die damit einhergehenden theoretischen Annahmen geben vor, welches Modell für die CFA spezifiziert und getestet werden sollte. Für das vorliegende Beispiel besagt unsere Theorie (bzw. die Theorie der Big Five), dass die Konstrukte Extraversion und Neurotizismus jeweils eindimensional und unkorreliert sind.
Wir spezifizieren daher ein zweidimensionales \(\tau\)-kongenerisches Modell mit Einfachstruktur und unkorrelierten Faktoren:
# Spezifikation des Testmodells
model <- "
e =~ E1 + E2 + E3 + E4 + E5 + E6 + E7 + E8 + E9 + E10 + E11 + E12
n =~ N1 + N2 + N3 + N4 + N5 + N6 + N7 + N8 + N9 + N10 + N11 + N12
n ~~ 0*e
"
# Schätzung und Evaluation der Modellpassung
fit_cfa_E_N <- cfa(model = model, data = neo,
std.lv = TRUE, meanstructure = TRUE, estimator = "ml")
summary(fit_cfa_E_N, standardized = TRUE, fit.measures = TRUE)model <- "
e =~ E1 + E2 + E3 + E4 + E5 + E6 + E7 + E8 + E9 + E10 + E11 + E12
n =~ N1 + N2 + N3 + N4 + N5 + N6 + N7 + N8 + N9 + N10 + N11 + N12
n ~~ 0*e
"
fit_cfa_E_N <- cfa(model = model, data = neo,
std.lv = TRUE, meanstructure = TRUE, estimator = "ml")
summary(fit_cfa_E_N, standardized = TRUE, fit.measures = TRUE)lavaan 0.6.17 ended normally after 16 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 72
Number of observations 566
Model Test User Model:
Test statistic 1349.121
Degrees of freedom 252
P-value (Chi-square) 0.000
Model Test Baseline Model:
Test statistic 5285.283
Degrees of freedom 276
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.781
Tucker-Lewis Index (TLI) 0.760
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -17951.291
Loglikelihood unrestricted model (H1) -17276.731
Akaike (AIC) 36046.582
Bayesian (BIC) 36358.961
Sample-size adjusted Bayesian (SABIC) 36130.395
Root Mean Square Error of Approximation:
RMSEA 0.088
90 Percent confidence interval - lower 0.083
90 Percent confidence interval - upper 0.092
P-value H_0: RMSEA <= 0.050 0.000
P-value H_0: RMSEA >= 0.080 0.997
Standardized Root Mean Square Residual:
SRMR 0.163
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
e =~
E1 0.517 0.041 12.636 0.000 0.517 0.530
E2 0.418 0.036 11.668 0.000 0.418 0.494
E3 0.788 0.042 18.721 0.000 0.788 0.725
E4 0.425 0.036 11.951 0.000 0.425 0.505
E5 0.378 0.046 8.218 0.000 0.378 0.360
E6 0.306 0.046 6.689 0.000 0.306 0.297
E7 0.502 0.042 12.039 0.000 0.502 0.508
E8 0.710 0.033 21.682 0.000 0.710 0.806
E9 0.751 0.043 17.282 0.000 0.751 0.683
E10 0.094 0.048 1.955 0.051 0.094 0.089
E11 0.471 0.040 11.860 0.000 0.471 0.501
E12 0.400 0.048 8.308 0.000 0.400 0.364
n =~
N1 0.211 0.044 4.761 0.000 0.211 0.207
N2 0.672 0.040 16.708 0.000 0.672 0.649
N3 0.872 0.047 18.628 0.000 0.872 0.704
N4 0.747 0.043 17.474 0.000 0.747 0.671
N5 0.764 0.041 18.403 0.000 0.764 0.698
N6 0.988 0.047 21.072 0.000 0.988 0.769
N7 0.636 0.044 14.298 0.000 0.636 0.572
N8 0.632 0.042 15.168 0.000 0.632 0.601
N9 0.802 0.042 19.128 0.000 0.802 0.718
N10 0.788 0.040 19.571 0.000 0.788 0.730
N11 0.941 0.042 22.454 0.000 0.941 0.803
N12 0.478 0.045 10.676 0.000 0.478 0.445
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
e ~~
n 0.000 0.000 0.000
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.E1 2.214 0.041 53.964 0.000 2.214 2.268
.E2 2.723 0.036 76.530 0.000 2.723 3.217
.E3 2.473 0.046 54.123 0.000 2.473 2.275
.E4 2.928 0.035 82.641 0.000 2.928 3.474
.E5 1.809 0.044 40.947 0.000 1.809 1.721
.E6 1.776 0.043 40.876 0.000 1.776 1.718
.E7 1.760 0.042 42.342 0.000 1.760 1.780
.E8 2.673 0.037 72.250 0.000 2.673 3.037
.E9 2.337 0.046 50.566 0.000 2.337 2.125
.E10 1.963 0.045 43.909 0.000 1.963 1.846
.E11 2.389 0.039 60.555 0.000 2.389 2.545
.E12 1.890 0.046 40.876 0.000 1.890 1.718
.N1 1.910 0.043 44.640 0.000 1.910 1.876
.N2 1.647 0.044 37.819 0.000 1.647 1.590
.N3 1.903 0.052 36.563 0.000 1.903 1.537
.N4 1.993 0.047 42.635 0.000 1.993 1.792
.N5 1.920 0.046 41.764 0.000 1.920 1.755
.N6 1.776 0.054 32.911 0.000 1.776 1.383
.N7 2.037 0.047 43.635 0.000 2.037 1.834
.N8 2.041 0.044 46.161 0.000 2.041 1.940
.N9 1.581 0.047 33.690 0.000 1.581 1.416
.N10 2.069 0.045 45.640 0.000 2.069 1.918
.N11 1.790 0.049 36.365 0.000 1.790 1.529
.N12 2.481 0.045 54.847 0.000 2.481 2.305
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.E1 0.685 0.044 15.717 0.000 0.685 0.720
.E2 0.541 0.034 15.907 0.000 0.541 0.756
.E3 0.560 0.041 13.621 0.000 0.560 0.474
.E4 0.529 0.033 15.854 0.000 0.529 0.745
.E5 0.962 0.059 16.402 0.000 0.962 0.870
.E6 0.974 0.059 16.551 0.000 0.974 0.912
.E7 0.725 0.046 15.837 0.000 0.725 0.742
.E8 0.271 0.024 11.488 0.000 0.271 0.350
.E9 0.646 0.045 14.317 0.000 0.646 0.534
.E10 1.122 0.067 16.800 0.000 1.122 0.992
.E11 0.659 0.042 15.871 0.000 0.659 0.749
.E12 1.050 0.064 16.392 0.000 1.050 0.868
.N1 0.992 0.059 16.749 0.000 0.992 0.957
.N2 0.622 0.040 15.632 0.000 0.622 0.579
.N3 0.772 0.051 15.204 0.000 0.772 0.504
.N4 0.679 0.044 15.476 0.000 0.679 0.549
.N5 0.614 0.040 15.261 0.000 0.614 0.513
.N6 0.672 0.047 14.433 0.000 0.672 0.408
.N7 0.830 0.052 16.025 0.000 0.830 0.673
.N8 0.707 0.044 15.898 0.000 0.707 0.639
.N9 0.604 0.040 15.071 0.000 0.604 0.484
.N10 0.543 0.036 14.943 0.000 0.543 0.467
.N11 0.486 0.035 13.824 0.000 0.486 0.355
.N12 0.929 0.057 16.419 0.000 0.929 0.802
e 1.000 1.000 1.000
n 1.000 1.000 1.000Erklärung des Codes:
- Modellspezifikation:
- Das \(\tau\)-kongenerische Modell umfasst zwei latente Variablen:
e: Extraversion (mit 12 Items E1 bis E12)n: Neurotizismus (mit 12 Items N1 bis N12)
n ~~ 0*e: Hier treffen wir die theoretische Annahme, dass die beiden Faktoren orthogonal sind, also nicht miteinander korrelieren. Eine solche Annahme ergibt nur Sinn, wenn Sie inhaltlich begründet aus der Konstruktdefinition oder dem nomologischen Netz hervor geht. Angenommen, unsere Konstruktdefinition beinhaltet zwei orthogonale Faktoren, dann ist die Betrachtung des Modellfits des spezifizierten Modells relevant für die Bewertung der faktoriellen Validität.
- Das \(\tau\)-kongenerische Modell umfasst zwei latente Variablen:
- CFA durchführen:
std.lv = TRUE: Standardisierung der latenten Variablen.meanstructure = TRUE: Schätzung der Mittelwerte.
- Ergebnisse ausgeben:
- Standardisierte Ladungen und Fit-Indikatoren werden durch
standardized = TRUEundfit.measures = TRUEausgegeben.
- Standardisierte Ladungen und Fit-Indikatoren werden durch
Ausgabe verstehen:
Model Test User Model:
Die Modellfit-Indikatoren helfen uns zu beurteilen, wie gut das theoretische Modell zu den empirischen Daten passt. Dabei müssen wir den p-Wert des User Models betrachten (nicht des Baseline Models). Hier ist der p-Wert signifikant (p < 0.05) und wir lehnen die Nullhypothese ab, dass das Modell in der Population gilt. Das theoretische Modell passt somit nicht perfekt zu den Daten.
Weitere Fit-Indizes:
Neben dem Modelltest betrachten wir folgende Indikatoren, die Sie aus der Vorlesung kennen:
- Comparative Fit Index (CFI): Der Cutoff-Wert liegt hier bei > 0.95 für einen guten Modellfit. Unsere Daten sprechen mit einem CFI von 0.781 für einen schlechten Modellfit.
- RMSEA: Der Cutoff-Wert bei großen Stichproben von N > 250 (Number of observations: 566) liegt bei < 0.06. Der beobachtete Wert von 0.088 liegt über dem Cutoff, was ebenfalls auf schlechten Fit hinweist.
- SRMR: Der Cutoff-Wert liegt bei < 0.11. Unser Wert von 0.163 deutet ebenfalls auf schlechten Fit hin.
Alle Fit-Indikatoren sprechen dafür, dass das Modell abgelehnt werden sollte. Dies spricht natürlich erst einmal gegen eine hohe faktorielle Validität. Welcher Aspekt unseres theoretischen Modells nicht mit den Daten kompatibel ist (und damit einhergehend, wie schwerwiegend dieser Befund bewertet werden muss), kann daraus jedoch noch nicht geschlossen werden.
Lokaler Modellfit:
Unter Latent Variables sehen wir die Ladungen der Items auf die latenten Variablen
- Für Extraversion: Fast alle Items laden signifikant auf den Faktor. Eine Ausnahme ist Item E10, dessen Ladung nicht signifikant ist. Auch die standardisierte Ladung (Std.all) ist bei E10 sehr gering.
- Für Neurotizismus: Alle Items laden signifikant, aber einige Items (z.B. N1) haben ebenfalls nur geringe Ladungen.
Unter Covariances sehen wir, dass die Korrelation zwischen den latenten Variablen 0 ist. Da dies von uns so spezifiziert wurde, wird kein Schätzwert und kein Standardfehler ausgegeben.
In einem explorativen Schritt könnten wir versuchen Ursachen für den schlechten Modellfit zu finden und das Modell eventuell modifizieren. Mögliche Ursachen könnten problematische Items sein, wie z.B. E10 oder N1, die nur schwach auf die latenten Faktoren laden. Dies wären Probleme, die auch im Rahmen der Skalierung relevant sind.
3.2.2 Explorative Modellanpassung: Modifikationsindizes
Da der ursprüngliche Modellfit unzureichend war, können wir explorativ prüfen, wie das Modell verbessert werden könnte. Ein Werkzeug hierfür sind die Modifikationsindizes, die Vorschläge zur Modellanpassung machen, um den Fit zu optimieren. Dabei handelt es sich jedoch nicht mehr wirklich um eine konfirmative Analyse, sondern um einen explorativen Schritt.
3.2.2.1 Modifikationsindizes berechnen
Der folgende Code berechnet die Modifikationsindizes und zeigt die vielversprechendsten Anpassungen:
mod_ind <- modindices(fit_cfa_E_N, sort.=TRUE, standardized = FALSE,
minimum.value = 4)mod_ind <- modindices(fit_cfa_E_N, sort.=TRUE, standardized = FALSE,
minimum.value = 4)
mod_ind lhs op rhs mi epc
25 e ~~ n 193.615 -0.662
347 N4 ~~ N10 92.564 0.276
104 E1 ~~ E4 65.824 0.220
106 E1 ~~ E6 51.479 0.257
192 E5 ~~ E10 50.790 0.315
105 E1 ~~ E5 40.072 0.227
98 n =~ E9 38.467 -0.235
151 E3 ~~ E8 37.789 0.160
194 E5 ~~ E12 33.340 0.251
212 E6 ~~ E12 30.790 0.241
228 E7 ~~ E11 28.373 0.165
110 E1 ~~ E10 28.137 0.202
242 E8 ~~ E9 25.663 0.133
196 E5 ~~ N2 24.464 -0.168
245 E8 ~~ E12 24.070 -0.137
169 E4 ~~ E6 20.299 0.141
108 E1 ~~ E8 20.229 -0.107
279 E10 ~~ N5 20.193 0.164
190 E5 ~~ E8 19.694 -0.118
273 E10 ~~ E11 17.908 0.158
326 N2 ~~ N6 17.690 0.131
375 N10 ~~ N11 17.638 -0.111
249 E8 ~~ N4 17.594 -0.092
81 e =~ N4 17.314 -0.162
130 E2 ~~ E8 16.510 0.085
208 E6 ~~ E8 15.881 -0.106
103 E1 ~~ E3 15.380 -0.121
148 E3 ~~ E5 14.572 -0.134
175 E4 ~~ E12 14.306 0.124
172 E4 ~~ E9 14.104 -0.105
101 n =~ E12 13.936 -0.170
99 n =~ E10 13.911 0.174
87 e =~ N10 13.357 -0.129
243 E8 ~~ E10 13.326 -0.102
316 N1 ~~ N6 13.247 -0.135
324 N2 ~~ N4 13.148 -0.108
153 E3 ~~ E10 12.907 -0.133
133 E2 ~~ E11 12.632 -0.095
220 E6 ~~ N8 12.511 -0.127
97 n =~ E8 12.130 -0.093
340 N3 ~~ N11 10.987 0.103
112 E1 ~~ E12 10.820 0.123
346 N4 ~~ N9 10.721 -0.099
168 E4 ~~ E5 10.678 0.102
301 E12 ~~ N2 10.521 -0.115
255 E8 ~~ N10 10.517 -0.064
296 E11 ~~ N9 10.405 -0.092
171 E4 ~~ E8 10.355 -0.067
240 E7 ~~ N11 10.245 -0.089
303 E12 ~~ N4 9.910 0.117
357 N6 ~~ N7 9.760 -0.110
317 N1 ~~ N7 8.717 0.116
92 n =~ E3 8.705 -0.106
134 E2 ~~ E12 8.469 -0.096
330 N2 ~~ N10 7.860 -0.077
189 E5 ~~ E7 7.628 0.101
373 N9 ~~ N11 7.562 0.076
100 n =~ E11 7.509 -0.100
323 N2 ~~ N3 7.212 -0.086
264 E9 ~~ N4 7.166 -0.083
193 E5 ~~ E11 7.062 0.093
109 E1 ~~ E9 6.959 -0.084
83 e =~ N6 6.914 -0.105
230 E7 ~~ N1 6.872 0.096
86 e =~ N9 6.786 -0.097
334 N3 ~~ N5 6.672 0.084
277 E10 ~~ N3 6.610 0.105
253 E8 ~~ N8 6.594 0.057
90 n =~ E1 6.359 0.095
247 E8 ~~ N2 6.357 0.052
282 E10 ~~ N8 6.213 0.096
341 N3 ~~ N12 6.151 -0.094
372 N9 ~~ N10 6.034 -0.068
374 N9 ~~ N12 6.020 0.083
132 E2 ~~ E10 6.001 -0.083
276 E10 ~~ N2 5.737 -0.087
291 E11 ~~ N4 5.594 0.071
154 E3 ~~ E11 5.581 -0.071
298 E11 ~~ N11 5.555 -0.063
217 E6 ~~ N5 5.538 -0.080
173 E4 ~~ E10 5.518 0.078
292 E11 ~~ N5 5.503 0.067
307 E12 ~~ N8 5.204 -0.086
348 N4 ~~ N11 5.174 -0.065
311 E12 ~~ N12 5.171 -0.097
315 N1 ~~ N5 5.094 0.078
258 E9 ~~ E10 5.036 -0.087
335 N3 ~~ N6 4.991 -0.079
368 N8 ~~ N9 4.834 -0.066
96 n =~ E7 4.769 -0.084
309 E12 ~~ N10 4.740 0.074
111 E1 ~~ E11 4.693 0.066
283 E10 ~~ N9 4.525 -0.077
270 E9 ~~ N10 4.522 -0.060
319 N1 ~~ N9 4.513 0.073
233 E7 ~~ N4 4.437 0.066
125 E2 ~~ E3 4.423 0.057
331 N2 ~~ N11 4.383 0.057
127 E2 ~~ E5 4.176 -0.065
147 E3 ~~ E4 4.122 -0.054
377 N11 ~~ N12 4.016 0.064
225 E7 ~~ E8 4.010 -0.049
352 N5 ~~ N8 4.009 0.060Erklärung des Codes
modindices(fit_cfa_E_N): Berechnet die Modifikationsindizes basierend auf unserem ursprünglichen Modellfit_cfa_E_N.sort.=TRUE: Sortiert die Indizes automatisch.minimum.value = 4: Es werden nur diejenigen Modifikationen, die einen Modifikationsindex größer als 4 haben angezeigt (Schwellenwert für signifikante Verbesserung).mod_ind: Die berechneten Werte werden in ein Objekt geschrieben.
Ausgabe verstehen:
- Pfade zwischen latenten Variablen:
e ~~ n: Der erste Modifikationsindex zeigt, dass das Modell deutlich verbessert würde, wenn eine Korrelation zwischen den latenten Faktoren Extraversion und Neurotizismus zugelassen wird (anstatt die Korrelation auf 0 zu fixieren).mi: Der Modifikationsindex gibt an, wie stark sich der \(\chi^{2}\)-Wert (Teststatistik des Modelltests) verbessern würde, wenn dieser Pfad freigegeben wird.ecp: Der erwartete Parameterwert (Expected Parameter Change), den der Pfad annehmen könnte, wenn wir ihn nicht mehr auf 0 fixieren. (Hinweis: Der tatsächlich geschätzte Wert weicht meistens etwas von epc ab)
- Residualkorrelationen zwischen Items:
- Der Index zeigt, dass eine Korrelation zwischen den Residuen der Neurotizismus-Items N4 und N10 eine erhebliche Verbesserung des Modells bewirken würde.
- Die Annahme des \(\tau\)-kongenerischen Modells ist, dass die Fehlervarianzen der Items unkorreliert sind. Das Modell scheint hier verletzt zu sein. Wir würden das Modell also deutlich verbessern, indem wir eine Korrelation zwischen den Items N4 und N10 zulassen
- Ladungen von Items auf andere Faktoren:
n =~ E9: Eine weitere spannende Modifikation wäre, Item E9 nicht nur auf Extraversion, sondern auch auf Neurotizismus laden zu lassen.- Dies deutet darauf hin, dass Item E9 eine Beziehung zu beiden latenten Faktoren hat und somit gegen die Einfachstruktur spricht.
Beispiele für problematische Items:
Betrachten wir nun die Itemtexte:
- N4: „Ich fühle mich selten einsam oder traurig.“
- N10: „Ich bin selten traurig oder deprimiert.“
Die ähnliche Formulierung der Items weist darauf hin, dass diese über den gemeinsamen Neurotizismushauptfaktor hinaus eine spezifische Beziehung haben. Das könnte eine zusätzliche Korrelation der Residuen rechtfertigen.
- E9: “Ich bin kein gutgelaunter Optimist”.
Dieses Item wird aktuell dem Faktor Extraversion zugeordnet. Der Modifikationsindex legt nahe, dass E9 auch auf den Faktor Neurotizismus laden sollte, da es inhaltlich auch negative Emotionen anspricht, die für Neurotizismus typisch sind.
Bei Betrachtung der Modifikationsindizes fällt neben verschiedenen Problemen mit einzelnen Items auf, dass die Annahme orthogonaler Faktoren vermutlich empirisch nicht haltbar ist.
3.2.3 Modifiziertes Modell mit korrelierten Faktoren testen
In einem weiteren Schritt passen wir das Modell an, indem wir den ersten Modifikationsindex umsetzen. Konkret bedeutet das, dass wir die Korrelation zwischen den latenten Faktoren Extraversion und Neurotizismus zulassen.
Das modifizierte Modell wird wie folgt definiert:
model_corr <- "
e =~ E1 + E2 + E3 + E4 + E5 + E6 + E7 + E8 + E9 + E10 + E11 + E12
n =~ N1 + N2 + N3 + N4 + N5 + N6 + N7 + N8 + N9 + N10 + N11 + N12
n ~~ e
"
fit_cfa_E_N_corr <- cfa(model = model_corr, data = neo,
std.lv = TRUE, meanstructure = TRUE, estimator = "ml")
summary(fit_cfa_E_N_corr, standardized = TRUE, fit.measures = TRUE)model_corr <- "
e =~ E1 + E2 + E3 + E4 + E5 + E6 + E7 + E8 + E9 + E10 + E11 + E12
n =~ N1 + N2 + N3 + N4 + N5 + N6 + N7 + N8 + N9 + N10 + N11 + N12
n ~~ e
"
fit_cfa_E_N_corr <- cfa(model = model_corr, data = neo,
std.lv = TRUE, meanstructure = TRUE, estimator = "ml")
summary(fit_cfa_E_N_corr, standardized = TRUE, fit.measures = TRUE)lavaan 0.6.17 ended normally after 19 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 73
Number of observations 566
Model Test User Model:
Test statistic 1107.490
Degrees of freedom 251
P-value (Chi-square) 0.000
Model Test Baseline Model:
Test statistic 5285.283
Degrees of freedom 276
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.829
Tucker-Lewis Index (TLI) 0.812
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -17830.476
Loglikelihood unrestricted model (H1) -17276.731
Akaike (AIC) 35806.951
Bayesian (BIC) 36123.668
Sample-size adjusted Bayesian (SABIC) 35891.928
Root Mean Square Error of Approximation:
RMSEA 0.078
90 Percent confidence interval - lower 0.073
90 Percent confidence interval - upper 0.082
P-value H_0: RMSEA <= 0.050 0.000
P-value H_0: RMSEA >= 0.080 0.208
Standardized Root Mean Square Residual:
SRMR 0.068
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
e =~
E1 0.486 0.041 11.862 0.000 0.486 0.498
E2 0.407 0.036 11.397 0.000 0.407 0.481
E3 0.793 0.042 19.076 0.000 0.793 0.729
E4 0.405 0.036 11.390 0.000 0.405 0.480
E5 0.353 0.046 7.703 0.000 0.353 0.336
E6 0.300 0.045 6.599 0.000 0.300 0.290
E7 0.507 0.041 12.267 0.000 0.507 0.512
E8 0.713 0.032 22.105 0.000 0.713 0.810
E9 0.781 0.042 18.402 0.000 0.781 0.710
E10 0.060 0.048 1.255 0.209 0.060 0.056
E11 0.476 0.039 12.109 0.000 0.476 0.507
E12 0.415 0.048 8.718 0.000 0.415 0.377
n =~
N1 0.212 0.044 4.790 0.000 0.212 0.208
N2 0.669 0.040 16.665 0.000 0.669 0.646
N3 0.865 0.047 18.461 0.000 0.865 0.698
N4 0.760 0.042 17.918 0.000 0.760 0.683
N5 0.763 0.041 18.427 0.000 0.763 0.698
N6 0.992 0.047 21.262 0.000 0.992 0.773
N7 0.631 0.044 14.196 0.000 0.631 0.568
N8 0.626 0.042 15.026 0.000 0.626 0.595
N9 0.805 0.042 19.266 0.000 0.805 0.721
N10 0.797 0.040 19.960 0.000 0.797 0.739
N11 0.930 0.042 22.140 0.000 0.930 0.794
N12 0.476 0.045 10.645 0.000 0.476 0.443
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
e ~~
n -0.671 0.029 -23.248 0.000 -0.671 -0.671
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.E1 2.214 0.041 53.964 0.000 2.214 2.268
.E2 2.723 0.036 76.530 0.000 2.723 3.217
.E3 2.473 0.046 54.123 0.000 2.473 2.275
.E4 2.928 0.035 82.641 0.000 2.928 3.474
.E5 1.809 0.044 40.947 0.000 1.809 1.721
.E6 1.776 0.043 40.876 0.000 1.776 1.718
.E7 1.760 0.042 42.342 0.000 1.760 1.780
.E8 2.673 0.037 72.250 0.000 2.673 3.037
.E9 2.337 0.046 50.566 0.000 2.337 2.125
.E10 1.963 0.045 43.909 0.000 1.963 1.846
.E11 2.389 0.039 60.555 0.000 2.389 2.545
.E12 1.890 0.046 40.876 0.000 1.890 1.718
.N1 1.910 0.043 44.640 0.000 1.910 1.876
.N2 1.647 0.044 37.818 0.000 1.647 1.590
.N3 1.903 0.052 36.563 0.000 1.903 1.537
.N4 1.993 0.047 42.635 0.000 1.993 1.792
.N5 1.920 0.046 41.764 0.000 1.920 1.755
.N6 1.776 0.054 32.911 0.000 1.776 1.383
.N7 2.037 0.047 43.635 0.000 2.037 1.834
.N8 2.041 0.044 46.161 0.000 2.041 1.940
.N9 1.581 0.047 33.689 0.000 1.581 1.416
.N10 2.069 0.045 45.640 0.000 2.069 1.918
.N11 1.790 0.049 36.365 0.000 1.790 1.529
.N12 2.481 0.045 54.847 0.000 2.481 2.305
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.E1 0.717 0.045 16.000 0.000 0.717 0.752
.E2 0.551 0.034 16.073 0.000 0.551 0.769
.E3 0.553 0.040 13.943 0.000 0.553 0.468
.E4 0.546 0.034 16.074 0.000 0.546 0.769
.E5 0.980 0.059 16.505 0.000 0.980 0.887
.E6 0.978 0.059 16.594 0.000 0.978 0.916
.E7 0.721 0.045 15.933 0.000 0.721 0.737
.E8 0.267 0.022 12.013 0.000 0.267 0.345
.E9 0.599 0.042 14.248 0.000 0.599 0.495
.E10 1.128 0.067 16.815 0.000 1.128 0.997
.E11 0.655 0.041 15.960 0.000 0.655 0.743
.E12 1.038 0.063 16.409 0.000 1.038 0.858
.N1 0.991 0.059 16.753 0.000 0.991 0.957
.N2 0.625 0.040 15.714 0.000 0.625 0.583
.N3 0.785 0.051 15.347 0.000 0.785 0.512
.N4 0.660 0.043 15.468 0.000 0.660 0.533
.N5 0.615 0.040 15.355 0.000 0.615 0.513
.N6 0.663 0.046 14.520 0.000 0.663 0.403
.N7 0.836 0.052 16.088 0.000 0.836 0.678
.N8 0.715 0.045 15.976 0.000 0.715 0.646
.N9 0.599 0.040 15.147 0.000 0.599 0.481
.N10 0.527 0.035 14.952 0.000 0.527 0.453
.N11 0.506 0.036 14.165 0.000 0.506 0.369
.N12 0.931 0.057 16.447 0.000 0.931 0.804
e 1.000 1.000 1.000
n 1.000 1.000 1.000Erklärung des Codes:
Die Grundstruktur bleibt unverändert: Der Code ist derselbe wie bei der ursprünglichen CFA, in der wir die faktorielle Validität getestet haben.
Wir nehmen folgende Änderungen im Modell vor:
n ~~ e: Wir erlauben eine Korrelation zwischen den Faktoren Extraversion und Neurotizismus, anstatt sie (wie zuvor:n ~~ 0*e) auf 0 zu fixieren. (Hinweis: Diese Korrelation könnte theoretisch auch weggelassen werden, da lavaan standardmäßig eine Korrelation zwischen Faktoren zulässt.)- Das Modell wird in
model_corrumbenannt, und die Analyse wird alsfit_cfa_E_N_corrgespeichert, um sie von der ursprünglichen Analyse zu unterscheiden.
Ausgabe verstehen:
Wir betrachten die Globalen Fitindikatoren:
- Model Test User Model:
- Die H0 wird weiterhin abgelehnt (p < 0.05): Das Modell beschreibt die Daten nicht perfekt.
- Weitere Indikatoren:
- CFI: Hat sich deutlich verbessert und liegt jetzt bei 0.829 (vorher 0.781). Dennoch erreicht der Wert nicht den wünschenswerten Grenzwert von > 0.95.
- RMSEA: Ebenfalls eine Verbesserung, aber mit 0.078 weiterhin über dem Grenzwert von < 0.06.
- SRMR: Hat sich auf 0.068 verbessert und liegt jetzt unter dem Grenzwert von 0.11, was auf einen akzeptablen Fit hindeutet.
- AIC/BIC: Beide Informationskriterien sind für dieses Modell niedriger als für das vorherige Modell ohne Korrelation zwischen den Faktoren. Das Modell mit Korrelation scheint also besser zu passen.
Insgesamt zeigen die meisten Indikatoren zwar eine Verbesserung, lehnen das Modell aber weiterhin ab. Der Fit bleibt unzureichend.
Parameterschätzungen:
- Item E10 bleibt problematisch, da es weiterhin nur gering auf Extraversion lädt und sich dadurch nicht gut in das Modell einfügt.
- Die zuvor auf 0 fixierte Kovarianz wird jetzt auf −0.671 geschätzt.
- Da die Faktoren standardisiert sind, entspricht die Kovarianz direkt der Korrelation.
Im modifizierten Modell wird die Korrelation zwischen den Faktoren Extraversion und Neurotizismus auf \(r = −0.671\) geschätzt. Für die Bewertung der Konstruktvalidität sollte diese Korrelation kritisch mit Bezug auf die Konstruktdefinition sowie das nomologischen Netz diskutiert werden.
Je nach Konstruktdefinition und nomologischem Netz kann der Schätzwert für die Korrelation zwischen den zwei Faktoren des Modells entweder der faktoriellen, der konvergenten oder der divergenten Validität zugeordnet werden. Eine Interpretation und Kategorisierung ist also immer nur basierend auf der zugrundeliegenden inhaltlichen Theorie möglich.
Auch wenn das Modell mit korrelierten Faktoren relativ einen besseren Fit aufweist, ist der absolute Modellfit nicht befriedigend. Das weist daraufhin, dass es eventuell ein Problem mit der spezifizierten Zuordnung der Items zu den beiden Faktoren gibt.
Um zu überprüfen, ob die Extraversion- und Neurotizismusfaktoren wirklich eindimensional sind, können wir zusätzlich eine explorative Faktorenanalyse (EFA) durchführen, bei der wir die Items beider Skalen gemeinsam analysieren. Ziel ist es, herauszufinden, wie viele Faktoren tatsächlich in den Daten enthalten sind.
Der folgende Code führt die Parallelanalyse durch:
fa.parallel(neo[, c(extra_items, neuro_items)],
fm = "ml",
fa = "fa",
quant = 0.95,
n.iter = 1000)fa.parallel(neo[, c(extra_items, neuro_items)],
fm = "ml",
fa = "fa",
quant = 0.95,
n.iter = 1000)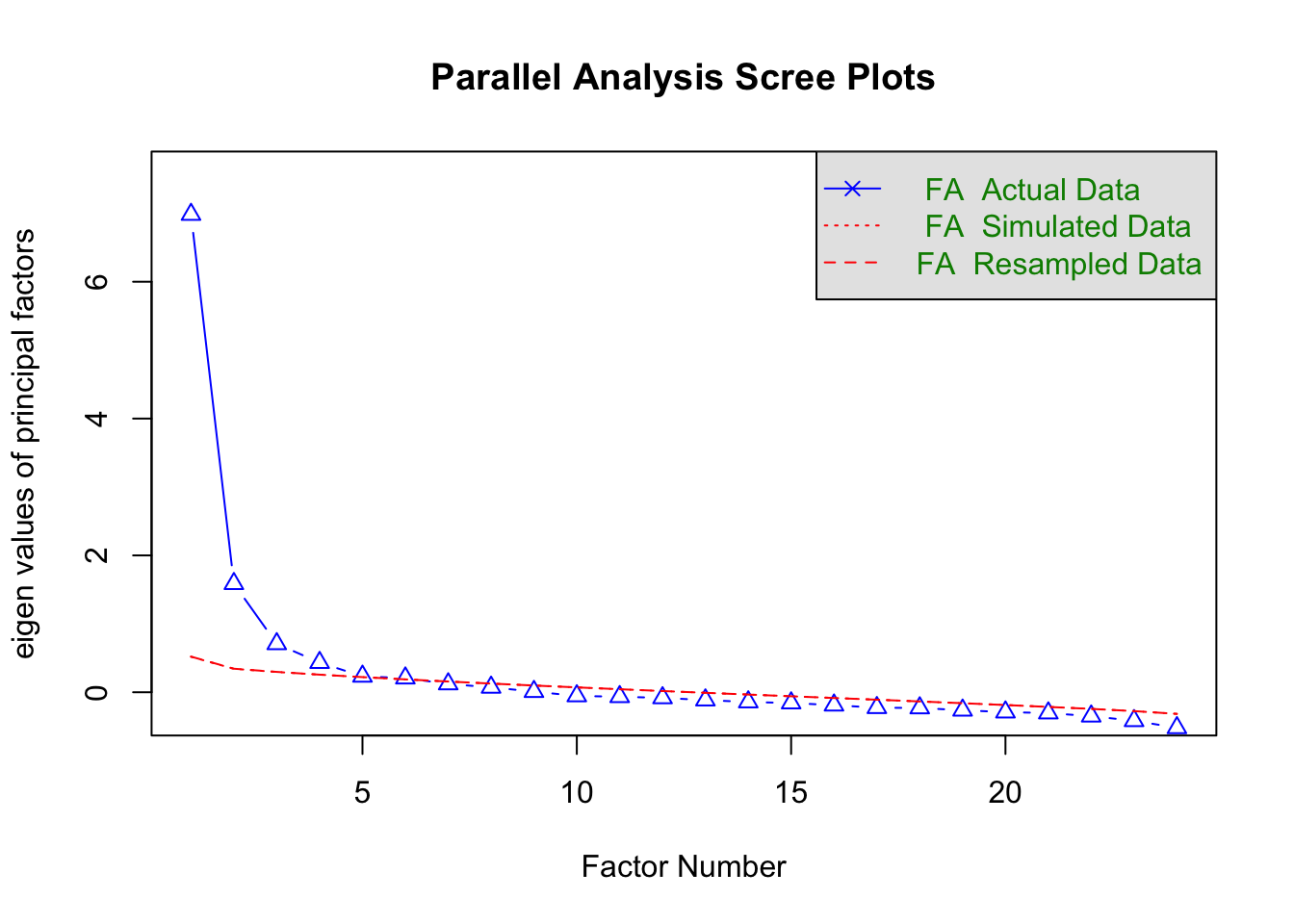
Parallel analysis suggests that the number of factors = 4 and the number of components = NA Für Details zur Funktionsweise der Parallelanalyse siehe das vorherige Tutorial zur Faktorenanalyse.
Ausgabe verstehen:
Ergebnis in der Konsole:
“Parallel analysis suggests that the number of factors = 4 and the number of components = NA”. Dies bedeutet, dass die Parallelanalyse vorschlägt, dass vier Faktoren in den Daten enthalten sind.Ergebnis im Plot:
Im Plot vergleichen wir die beobachteten Eigenwerte (blaue Dreiecke) mit dem 95%-Quantil der simulierten Eigenwerte (rote Linie). Der vierte Faktor liegt gerade noch knapp über der roten Linie, was darauf hinweist, dass er als „real“ interpretiert werden könnte. Alle weiteren Faktoren liegen unter der roten Linie und werden als zufällige Effekte angesehen.
Der Vorschlag der Parallelanalyse basiert auf den empirischen Daten und deutet darauf hin, dass die Items von Extraversion und Neurotizismus zusammen nicht nur auf zwei Faktoren (eindimensional für jeden) laden, sondern möglicherweise vier Dimensionen umfassen.
Auf Basis der Ergebnisse könnten wir nun eine EFA mit vier Faktoren durchführen, um zu prüfen, welche Items auf welchen Faktoren laden. Daraus könnten wir weitere Erkenntnisse gewinnen, die unsere bestehende Theorie überarbeiten.
3.3 Kriteriumsvalidität
Die Kriteriumsvalidität beschreibt, ob ein latenter Faktor, wie Neurotizismus, mit einem externen Kriterium korreliert, das theoretisch mit ihm zusammenhängen sollte. In diesem Fall prüfen wir die Korrelation von Neurotizismus mit den Kriterien Alter und Geschlecht. Dabei nehmen wir an, dass beide Kriterien messfehlerfrei erfasst wurde.
3.3.1 CFA mit Neurotizismus und dem Kriterium Alter
Wir erweitern unser Modell um die Korrelation zwischen dem latenten Faktor Neurotizismus und der Variablen Alter. Wir nehmen an, dass unsere Theorie besagt, dass das Konstrukt Neurotizismus negativ mit der messfehlerfreien Variable Alter korreliert.
model_age <- "
n =~ N1 + N2 + N3 + N4 + N5 + N6 + N7 + N8 + N9 + N10 + N11 + N12
n ~~ Age
"
fit_cfa_N_age <- cfa(model = model_age, data = neo,
std.lv = TRUE, meanstructure = TRUE, estimator = "ml")
summary(fit_cfa_N_age, standardized = TRUE, fit.measures = TRUE)model_age <- "
n =~ N1 + N2 + N3 + N4 + N5 + N6 + N7 + N8 + N9 + N10 + N11 + N12
n ~~ Age
"
fit_cfa_N_age <- cfa(model = model_age, data = neo,
std.lv = TRUE, meanstructure = TRUE, estimator = "ml")
summary(fit_cfa_N_age, standardized = TRUE, fit.measures = TRUE)lavaan 0.6.17 ended normally after 23 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 39
Number of observations 566
Model Test User Model:
Test statistic 260.882
Degrees of freedom 65
P-value (Chi-square) 0.000
Model Test Baseline Model:
Test statistic 2874.427
Degrees of freedom 78
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.930
Tucker-Lewis Index (TLI) 0.916
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -11203.237
Loglikelihood unrestricted model (H1) -11072.796
Akaike (AIC) 22484.475
Bayesian (BIC) 22653.680
Sample-size adjusted Bayesian (SABIC) 22529.873
Root Mean Square Error of Approximation:
RMSEA 0.073
90 Percent confidence interval - lower 0.064
90 Percent confidence interval - upper 0.082
P-value H_0: RMSEA <= 0.050 0.000
P-value H_0: RMSEA >= 0.080 0.110
Standardized Root Mean Square Residual:
SRMR 0.038
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
n =~
N1 0.212 0.044 4.775 0.000 0.212 0.208
N2 0.672 0.040 16.705 0.000 0.672 0.648
N3 0.872 0.047 18.629 0.000 0.872 0.704
N4 0.747 0.043 17.499 0.000 0.747 0.672
N5 0.763 0.042 18.388 0.000 0.763 0.698
N6 0.987 0.047 21.065 0.000 0.987 0.769
N7 0.635 0.044 14.292 0.000 0.635 0.572
N8 0.631 0.042 15.146 0.000 0.631 0.600
N9 0.802 0.042 19.133 0.000 0.802 0.718
N10 0.787 0.040 19.568 0.000 0.787 0.730
N11 0.941 0.042 22.465 0.000 0.941 0.803
N12 0.480 0.045 10.710 0.000 0.480 0.446
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
n ~~
Age -1.409 0.470 -3.001 0.003 -1.409 -0.132
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.N1 1.910 0.043 44.640 0.000 1.910 1.876
.N2 1.647 0.044 37.818 0.000 1.647 1.590
.N3 1.903 0.052 36.563 0.000 1.903 1.537
.N4 1.993 0.047 42.635 0.000 1.993 1.792
.N5 1.920 0.046 41.764 0.000 1.920 1.755
.N6 1.776 0.054 32.911 0.000 1.776 1.383
.N7 2.037 0.047 43.635 0.000 2.037 1.834
.N8 2.041 0.044 46.161 0.000 2.041 1.940
.N9 1.581 0.047 33.689 0.000 1.581 1.416
.N10 2.069 0.045 45.639 0.000 2.069 1.918
.N11 1.790 0.049 36.365 0.000 1.790 1.529
.N12 2.481 0.045 54.847 0.000 2.481 2.305
Age 30.723 0.450 68.208 0.000 30.723 2.867
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.N1 0.991 0.059 16.749 0.000 0.991 0.957
.N2 0.622 0.040 15.634 0.000 0.622 0.580
.N3 0.772 0.051 15.207 0.000 0.772 0.504
.N4 0.678 0.044 15.473 0.000 0.678 0.548
.N5 0.614 0.040 15.268 0.000 0.614 0.513
.N6 0.673 0.047 14.441 0.000 0.673 0.408
.N7 0.830 0.052 16.027 0.000 0.830 0.673
.N8 0.708 0.045 15.903 0.000 0.708 0.640
.N9 0.604 0.040 15.073 0.000 0.604 0.484
.N10 0.543 0.036 14.948 0.000 0.543 0.467
.N11 0.486 0.035 13.825 0.000 0.486 0.354
.N12 0.928 0.056 16.417 0.000 0.928 0.801
Age 114.833 6.826 16.823 0.000 114.833 1.000
n 1.000 1.000 1.000Ergebnisse:
Der Modellfit bleibt problematisch (CFI und RMSEA sind knapp außerhalb der akzeptablen Grenzen). Zu Demonstrationszwecken nehmen wir jedoch an, dass das Modell passt.
Unter „Covariances“ zeigt sich: Korrelation: −0.132
Für die Bewertung der Kriteriumsvalidität erhalten wir eine geschätzte Korrelation zwischen Neurotizismus und Alter von \(r = -0.132\), d.h. ältere Personen scheinen im Mittel etwas niedrigere Neurotizismuswerte zu haben als jüngere. Dies entspricht unserer theoretischen Annahme (und auch früheren empirischen Befunden) und ist somit im Sinne der Kriteriumsvalidität eher positiv zu bewerten.
Ob ein empirisch gefundener Zusammenhang für oder gegen die Kriteriumsvalidität spricht, hängt von der jeweiligen Konstruktdefinition sowie dem nomologischen Netzwerk ab.
Mit dem folgenden Befehl aus dem semPlot-Paket visualisieren wir das geschätzte Modell:
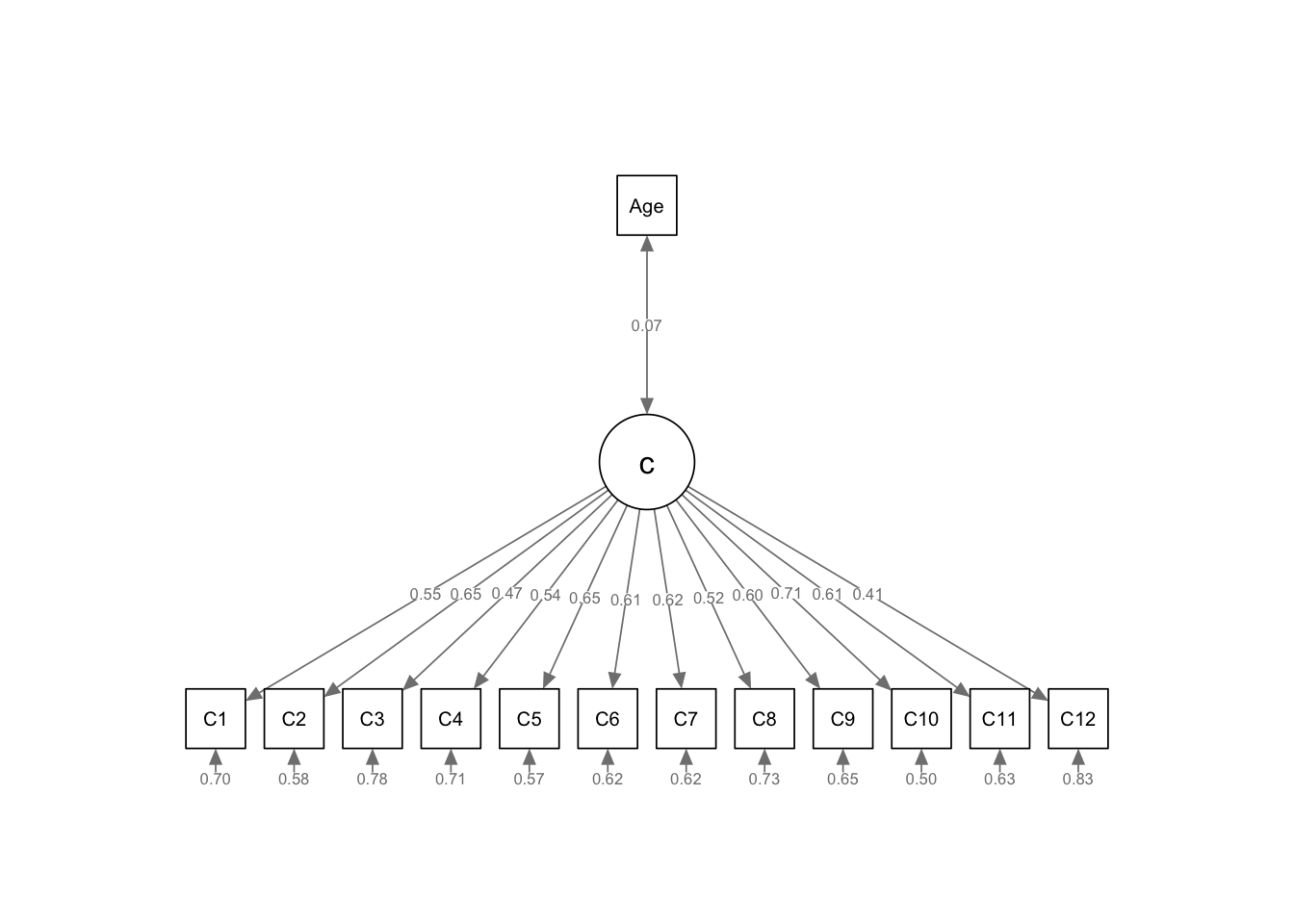
semPlot::semPaths(fit_cfa_N_age, whatLabels = "std", intercepts = FALSE,
style = "lisrel", layout = "tree2", rotation = 1)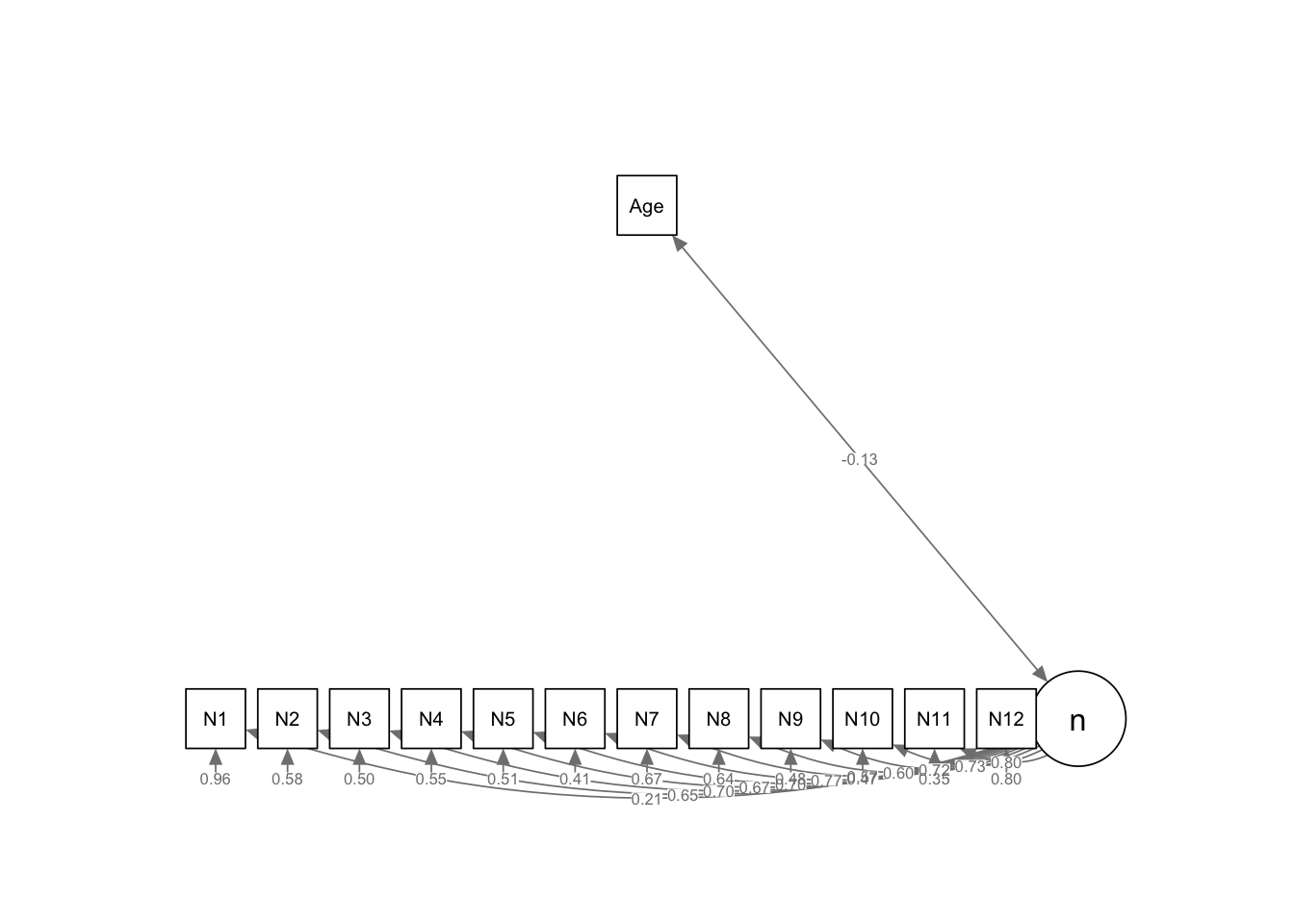
Der latente Faktor n wird als Kreis dargestellt, die manifeste Variable Age ist als Rechteck hinzugefügt und korreliert mit n.
3.3.2 CFA mit Neurotizismus und dem Kriterium Geschlecht
Analog erweitern wir das Modell, um die Korrelation zwischen Neurotizismus und Geschlecht zu untersuchen. Wir nehmen an, dass unsere Theorie besagt, dass das Konstrukt Neurotizismus positiv mit der messfehlerfreien Variable Geschlecht (0 = Männer, 1 = Frauen) korreliert, d.h., dass Frauen im Schnitt höhere Neurotizismuswerte haben.
model_sex <- "
n =~ N1 + N2 + N3 + N4 + N5 + N6 + N7 + N8 + N9 + N10 + N11 + N12
n ~~ Sex
"
fit_cfa_N_sex <- cfa(model = model_sex, data = neo,
std.lv = TRUE, meanstructure = TRUE, estimator = "ml")
summary(fit_cfa_N_sex, standardized = TRUE, fit.measures = TRUE)model_sex <- "
n =~ N1 + N2 + N3 + N4 + N5 + N6 + N7 + N8 + N9 + N10 + N11 + N12
n ~~ Sex
"
fit_cfa_N_sex <- cfa(model = model_sex, data = neo,
std.lv = TRUE, meanstructure = TRUE, estimator = "ml")
summary(fit_cfa_N_sex, standardized = TRUE, fit.measures = TRUE)lavaan 0.6.17 ended normally after 19 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 39
Number of observations 566
Model Test User Model:
Test statistic 260.488
Degrees of freedom 65
P-value (Chi-square) 0.000
Model Test Baseline Model:
Test statistic 2896.762
Degrees of freedom 78
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.931
Tucker-Lewis Index (TLI) 0.917
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -9424.064
Loglikelihood unrestricted model (H1) -9293.820
Akaike (AIC) 18926.127
Bayesian (BIC) 19095.333
Sample-size adjusted Bayesian (SABIC) 18971.526
Root Mean Square Error of Approximation:
RMSEA 0.073
90 Percent confidence interval - lower 0.064
90 Percent confidence interval - upper 0.082
P-value H_0: RMSEA <= 0.050 0.000
P-value H_0: RMSEA >= 0.080 0.108
Standardized Root Mean Square Residual:
SRMR 0.038
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
n =~
N1 0.210 0.044 4.744 0.000 0.210 0.206
N2 0.672 0.040 16.732 0.000 0.672 0.649
N3 0.874 0.047 18.688 0.000 0.874 0.706
N4 0.744 0.043 17.394 0.000 0.744 0.669
N5 0.763 0.042 18.377 0.000 0.763 0.697
N6 0.986 0.047 21.040 0.000 0.986 0.768
N7 0.637 0.044 14.338 0.000 0.637 0.573
N8 0.632 0.042 15.174 0.000 0.632 0.601
N9 0.802 0.042 19.139 0.000 0.802 0.718
N10 0.786 0.040 19.527 0.000 0.786 0.729
N11 0.943 0.042 22.533 0.000 0.943 0.805
N12 0.479 0.045 10.698 0.000 0.479 0.445
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
n ~~
Sex 0.115 0.020 5.649 0.000 0.115 0.245
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.N1 1.910 0.043 44.640 0.000 1.910 1.876
.N2 1.647 0.044 37.818 0.000 1.647 1.590
.N3 1.903 0.052 36.563 0.000 1.903 1.537
.N4 1.993 0.047 42.635 0.000 1.993 1.792
.N5 1.920 0.046 41.764 0.000 1.920 1.755
.N6 1.776 0.054 32.911 0.000 1.776 1.383
.N7 2.037 0.047 43.635 0.000 2.037 1.834
.N8 2.041 0.044 46.161 0.000 2.041 1.940
.N9 1.581 0.047 33.689 0.000 1.581 1.416
.N10 2.069 0.045 45.639 0.000 2.069 1.918
.N11 1.790 0.049 36.365 0.000 1.790 1.529
.N12 2.481 0.045 54.847 0.000 2.481 2.305
Sex 0.666 0.020 33.601 0.000 0.666 1.412
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.N1 0.992 0.059 16.750 0.000 0.992 0.957
.N2 0.621 0.040 15.636 0.000 0.621 0.579
.N3 0.769 0.051 15.201 0.000 0.769 0.502
.N4 0.683 0.044 15.503 0.000 0.683 0.553
.N5 0.615 0.040 15.279 0.000 0.615 0.514
.N6 0.675 0.047 14.464 0.000 0.675 0.410
.N7 0.828 0.052 16.025 0.000 0.828 0.671
.N8 0.707 0.044 15.904 0.000 0.707 0.639
.N9 0.603 0.040 15.081 0.000 0.603 0.484
.N10 0.545 0.036 14.971 0.000 0.545 0.469
.N11 0.483 0.035 13.808 0.000 0.483 0.352
.N12 0.928 0.057 16.421 0.000 0.928 0.802
Sex 0.222 0.013 16.823 0.000 0.222 1.000
n 1.000 1.000 1.000Ergebnisse: Die Korrelation beträgt 0.245.
Hinweis: Die Geschlechtsvariable ist mit 0 (Männer) und 1 (Frauen) kodiert.
Für die Bewertung der Kriteriumsvalidität erhalten wir eine geschätzte Korrelation zwischen Neurotizismus und Geschlecht von \(r = 0.245\), d.h. Frauen scheinen im Mittel etwas höhere Neurotizismuswerte zu haben als Männer. Dies entspricht unserer theoretischen Annahme (und auch früheren empirischen Befunden) und ist somit im Sinne der Kriteriumsvalidität eher positiv zu bewerten.
Ob ein empirisch gefundener Zusammenhang für oder gegen die Kriteriumsvalidität spricht, hängt von der jeweiligen Konstruktdefinition sowie dem nomologischen Netzwerk ab.
3.4 Vereinfachte Auswertung Teil 2: Die Minderungskorrektur
In unseren vereinfachten Auswertung zu Beginn des Validitätskapitels hatten wir zur Bewertung der unterschiedlichen Validitätsarten verschieden Korrelationen berechnet. Dabei wurde nicht berücksichtigt, dass Summenwerte einer Skala immer mit Messfehler behaftet sind.
Man kann mathematisch zeigen, dass bei nicht perfekter Reliabilität, die wahren Korrelationen von Konstrukten untereinander oder zwischen Konstrukten und messfehlerfreien Kriterien im Mittel höher sein sollten, als die beobachteten Korrelationen mit den Summenwerten. Dazu passend haben wir in den modellbasierten Analysen mithilfe der CFA und EFA (welche den Messfehler im Sinne der Reliabilität mit berücksichtigen) höhere Schätzwerte für die Zusammenhänge erhalten als in den Korrelationsmatrizen.
Alternativ zu den modellbasierten Verfahren gibt es die Möglichkeit, mithilfe der Minderungskorrektur die Korrelationen mit den Summenwerten so zu korrigieren, dass die Reliabilität der Skala berücksichtigt wird.
Früher, als die Durchführung von Faktorenanalysen noch sehr aufwändig war, war die Minderungskorrektur die einzige Möglichkeit, um bei der Schätzung der Zusammenhänge mit Konstrukten die Reliabilität zu berücksichtigen. Heute sollte die modellbasierte Schätzung der Zusammenhänge mithilfe der CFA oder EFA bevorzugt eingesetzt werden, da die Durchführung der Minderungskorrektur die gleichen strengen Annahmen voraussetzt, ohne dass diese jedoch mit der Methode selbst überprüft werden können!
3.4.1 Faktorielle, Konvergente oder Divergente Validität
Die beobachtete Korrelation zwischen den Summenwerten der Extraversions- und der Neurotizismusskala beträgt:
cor(neo$E_sum, neo$N_sum)[1] -0.5086277Da im Rahmen der faktoriellen, konvergenten und divergenten Konstruktvalidität stets Zusammenhänge zwischen zwei Konstrukten untersucht werden, sollte hier eine doppelte Minderungskorrektiur verwendet werden. D.h. es wird für die Ungenauigkeit der Skalenwerte beider Konstrukte korrigiert.
(Doppelte) Minderungskorrektur anwenden:
cor(neo$E_sum, neo$N_sum) / sqrt(alpha_extra$est * alpha_neuro$est)[1] -0.6039526Die einfache Korrelation der Summenwerte beträgt −0.509. Dieser Wert ist schwächer als die im Modell geschätzte Korrelation der latenten Variablen (−0.67). Nach Anwendung der Minderungskorrektur liegt die korrigierte Korrelation mit -0.60 näher am Modellwert (−0.67).
Wir haben hier Cronbachs Alpha als Reliabilitätsschätzung für die Minderungskorrektur verwendet, welches eine Mindestschätzung der Reliabilität darstellt (sofern nicht das (essentiell) parallele oder (essentiell) tau-äquivalente Modell gilt). Das bedeutet jedoch im Umkehrschluss, dass die Minderungskorrektur mithilfe von Cronbachs Alpha tendenziell die Höhe der Korrelation zwischen den Konstrukten überschätzt (Reliabilität im Nenner der Formel). Alternativ könnten wir auch McDonalds Omega verwenden, falls wir davon ausgehen wollen, dass das \(\tau\)-kongenerische Modell gilt.
3.4.2 Kriteriumsvalidität
Die beobachteten Korrelationen zwischen der Neurotizismusskala und den Kriterien Alter und Geschlecht betragen:
cor(neo$N_sum, neo$Age)[1] -0.133042cor(neo$N_sum, neo$Sex)[1] 0.2301819Da im Rahmen der Kriteriumsvalidität stets Zusammenhänge zwischen einem Konstrukt und einer messfehlerfreien Variable untersucht werden, sollte hier nur eine einfache Minderungskorrektiur verwendet werden. D.h. es wird nur für die Ungenauigkeit des Skalenwerte des Konstrukts korrigiert.
(Einfache) Minderungskorrektur anwenden:
cor(neo$N_sum, neo$Age) / sqrt(alpha_neuro$est)[1] -0.1410719cor(neo$N_sum, neo$Sex) / sqrt(alpha_neuro$est)[1] 0.2440748Ergebnisse:
Neurotizismus und Alter: Die Korrelation der Summenwerte zwischen Neurotizismus und Alter beträgt −0.133 und ist somit ähnlich wie der im Modell geschätzte Wert. Nach Anwendung der Minderungskorrektur erhöht sich die Korrelation leicht auf −0.141.
Neurotizismus und Geschlecht: Die Korrelation der Summenwerte zwischen Neurotizismus und Geschlecht beträgt 0.244 (nach Korrektur). Dieser Wert stimmt nahezu exakt mit dem im Modell geschätzten Wert von Std.all = 0.245 überein.
4 Arbeitsauftrag
Wiederholen Sie die Analysen aus dem Video mit der Skala Gewissenhaftigkeit (Variablennamen: C1, C2, … , C12) des Beispieldatensatzes (NEO_original.csv):
- Prüfen Sie die Reliabilität der Skala.
- Prüfen Sie die faktorielle Validität der Skala zusammen mit der Skala Neurotizismus um die Konstruktvalidität zu bewerten. Betrachten Sie dabei auch die Modifikationsindizes.
- Prüfen Sie die Kriteriumsvalidität der Skala anhand des Kriteriums Alter (als Hinweis: mit höherem Alter sollten Personen eine höhere Gewissenhaftigkeit aufweisen).
## Beispieldatensatz laden & für die Analysen vorbereiten
neo <- read.csv("NEO_original.csv")
# Vektoren mit Namen der gewünschten Spalten
gewiss_items <- c("C1", "C2", "C3", "C4", "C5", "C6",
"C7", "C8", "C9", "C10", "C11", "C12")
neuro_items <- c("N1", "N2", "N3", "N4", "N5", "N6",
"N7", "N8", "N9", "N10", "N11", "N12")
# Summwenwerte berechnen
neo$C_sum <- rowSums(neo[,gewiss_items])
neo$N_sum <- rowSums(neo[,neuro_items])
## Reliabilität
# Alpha
alpha_gewiss <- ci.reliability(neo[, gewiss_items], type = 'alpha', interval.type = "ml")
alpha_neuro <- ci.reliability(neo[, neuro_items], type = 'alpha', interval.type = "ml")
# Omega
omega_gewiss <- ci.reliability(neo[, gewiss_items], type = 'omega', interval.type = "ml")
omega_neuro <- ci.reliability(neo[, neuro_items], type = 'omega', interval.type = "ml")
## Konstruktvalidität: Faktorielle Validität
# CFA (-> Test ob Faktorstruktur der Theorie entspricht)
model <- "
c =~ C1 + C2 + C3 + C4 + C5 + C6 + C7 + C8 + C9 + C10 + C11 + C12
n =~ N1 + N2 + N3 + N4 + N5 + N6 + N7 + N8 + N9 + N10 + N11 + N12
n ~~ 0*c
"
fit_cfa_C_N <- cfa(model = model, data = neo, std.lv = TRUE, meanstructure = TRUE, estimator = "ML")
summary(fit_cfa_C_N, standardized=TRUE, fit.measures=TRUE) # Output inkl. Fit-Indikatorenlavaan 0.6.17 ended normally after 19 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 72
Number of observations 566
Model Test User Model:
Test statistic 1197.852
Degrees of freedom 252
P-value (Chi-square) 0.000
Model Test Baseline Model:
Test statistic 5547.954
Degrees of freedom 276
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.821
Tucker-Lewis Index (TLI) 0.804
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -17249.775
Loglikelihood unrestricted model (H1) -16650.849
Akaike (AIC) 34643.550
Bayesian (BIC) 34955.929
Sample-size adjusted Bayesian (SABIC) 34727.363
Root Mean Square Error of Approximation:
RMSEA 0.081
90 Percent confidence interval - lower 0.077
90 Percent confidence interval - upper 0.086
P-value H_0: RMSEA <= 0.050 0.000
P-value H_0: RMSEA >= 0.080 0.700
Standardized Root Mean Square Residual:
SRMR 0.140
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
c =~
C1 0.512 0.039 13.141 0.000 0.512 0.544
C2 0.701 0.043 16.190 0.000 0.701 0.645
C3 0.478 0.043 11.103 0.000 0.478 0.471
C4 0.341 0.026 13.052 0.000 0.341 0.541
C5 0.619 0.037 16.513 0.000 0.619 0.655
C6 0.719 0.048 15.116 0.000 0.719 0.611
C7 0.529 0.034 15.476 0.000 0.529 0.623
C8 0.338 0.027 12.365 0.000 0.338 0.517
C9 0.636 0.044 14.617 0.000 0.636 0.595
C10 0.566 0.031 18.325 0.000 0.566 0.709
C11 0.638 0.042 15.148 0.000 0.638 0.612
C12 0.409 0.043 9.484 0.000 0.409 0.409
n =~
N1 0.211 0.044 4.761 0.000 0.211 0.207
N2 0.672 0.040 16.708 0.000 0.672 0.649
N3 0.872 0.047 18.628 0.000 0.872 0.704
N4 0.747 0.043 17.474 0.000 0.747 0.671
N5 0.764 0.041 18.403 0.000 0.764 0.698
N6 0.988 0.047 21.072 0.000 0.988 0.769
N7 0.636 0.044 14.298 0.000 0.636 0.572
N8 0.632 0.042 15.168 0.000 0.632 0.601
N9 0.802 0.042 19.128 0.000 0.802 0.718
N10 0.788 0.040 19.571 0.000 0.788 0.730
N11 0.941 0.042 22.454 0.000 0.941 0.803
N12 0.478 0.045 10.676 0.000 0.478 0.445
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
c ~~
n 0.000 0.000 0.000
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.C1 2.650 0.040 67.033 0.000 2.650 2.818
.C2 2.495 0.046 54.653 0.000 2.495 2.297
.C3 2.611 0.043 61.135 0.000 2.611 2.570
.C4 3.352 0.027 126.457 0.000 3.352 5.315
.C5 2.459 0.040 61.970 0.000 2.459 2.605
.C6 1.989 0.049 40.216 0.000 1.989 1.690
.C7 2.726 0.036 76.338 0.000 2.726 3.209
.C8 3.408 0.028 123.816 0.000 3.408 5.204
.C9 2.555 0.045 56.813 0.000 2.555 2.388
.C10 2.834 0.034 84.493 0.000 2.834 3.551
.C11 2.797 0.044 63.800 0.000 2.797 2.682
.C12 2.558 0.042 60.779 0.000 2.558 2.555
.N1 1.910 0.043 44.640 0.000 1.910 1.876
.N2 1.647 0.044 37.818 0.000 1.647 1.590
.N3 1.903 0.052 36.563 0.000 1.903 1.537
.N4 1.993 0.047 42.635 0.000 1.993 1.792
.N5 1.920 0.046 41.764 0.000 1.920 1.755
.N6 1.776 0.054 32.911 0.000 1.776 1.383
.N7 2.037 0.047 43.635 0.000 2.037 1.834
.N8 2.041 0.044 46.161 0.000 2.041 1.940
.N9 1.581 0.047 33.689 0.000 1.581 1.416
.N10 2.069 0.045 45.639 0.000 2.069 1.918
.N11 1.790 0.049 36.365 0.000 1.790 1.529
.N12 2.481 0.045 54.847 0.000 2.481 2.305
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.C1 0.623 0.040 15.735 0.000 0.623 0.704
.C2 0.688 0.046 14.976 0.000 0.688 0.584
.C3 0.804 0.050 16.089 0.000 0.804 0.778
.C4 0.281 0.018 15.752 0.000 0.281 0.707
.C5 0.509 0.034 14.874 0.000 0.509 0.571
.C6 0.868 0.057 15.282 0.000 0.868 0.627
.C7 0.442 0.029 15.185 0.000 0.442 0.612
.C8 0.314 0.020 15.881 0.000 0.314 0.733
.C9 0.740 0.048 15.408 0.000 0.740 0.646
.C10 0.317 0.022 14.199 0.000 0.317 0.497
.C11 0.680 0.045 15.273 0.000 0.680 0.625
.C12 0.835 0.051 16.306 0.000 0.835 0.833
.N1 0.992 0.059 16.749 0.000 0.992 0.957
.N2 0.622 0.040 15.632 0.000 0.622 0.579
.N3 0.772 0.051 15.204 0.000 0.772 0.504
.N4 0.679 0.044 15.476 0.000 0.679 0.549
.N5 0.614 0.040 15.261 0.000 0.614 0.513
.N6 0.672 0.047 14.433 0.000 0.672 0.408
.N7 0.830 0.052 16.025 0.000 0.830 0.673
.N8 0.707 0.044 15.898 0.000 0.707 0.639
.N9 0.604 0.040 15.071 0.000 0.604 0.484
.N10 0.543 0.036 14.943 0.000 0.543 0.467
.N11 0.486 0.035 13.824 0.000 0.486 0.355
.N12 0.929 0.057 16.419 0.000 0.929 0.802
c 1.000 1.000 1.000
n 1.000 1.000 1.000# Prüfung des lokalen Fit im Modell (-> Indikator, welche Aspekte des Modell modifiziert werden könnten)
mod_ind <- modindices(fit_cfa_C_N, sort.=TRUE, standardized = FALSE)
subset(mod_ind[order(mod_ind$mi, decreasing=TRUE), ], mi > 4) lhs op rhs mi epc
25 c ~~ n 103.749 -0.482
347 N4 ~~ N10 92.563 0.276
86 c =~ N9 61.684 -0.289
100 n =~ C11 58.555 -0.290
189 C5 ~~ C7 48.956 0.160
229 C7 ~~ C12 40.915 0.176
242 C8 ~~ C9 40.097 0.139
128 C2 ~~ C6 38.630 0.229
171 C4 ~~ C8 32.042 0.076
287 C11 ~~ C12 26.758 -0.176
129 C2 ~~ C7 24.575 -0.131
111 C1 ~~ C11 24.454 0.148
101 n =~ C12 21.813 0.190
227 C7 ~~ C10 21.395 0.086
88 c =~ N11 19.896 -0.153
126 C2 ~~ C4 19.644 -0.091
95 n =~ C6 19.468 -0.189
175 C4 ~~ C12 19.119 0.094
107 C1 ~~ C7 19.101 -0.106
228 C7 ~~ C11 19.009 -0.113
326 N2 ~~ N6 17.690 0.131
375 N10 ~~ N11 17.638 -0.111
190 C5 ~~ C8 17.226 -0.077
134 C2 ~~ C12 16.941 -0.142
304 C12 ~~ N5 16.242 0.128
238 C7 ~~ N9 16.003 -0.095
133 C2 ~~ C11 15.635 0.129
173 C4 ~~ C10 14.713 0.055
316 N1 ~~ N6 13.247 -0.135
324 N2 ~~ N4 13.148 -0.108
85 c =~ N8 11.982 0.135
169 C4 ~~ C6 11.778 -0.078
212 C6 ~~ C12 11.502 -0.130
340 N3 ~~ N11 10.987 0.103
154 C3 ~~ C11 10.807 0.110
346 N4 ~~ N9 10.721 -0.099
153 C3 ~~ C10 10.036 -0.076
92 n =~ C3 9.851 -0.126
357 N6 ~~ N7 9.760 -0.110
132 C2 ~~ C10 9.689 -0.073
231 C7 ~~ N2 9.676 -0.074
102 C1 ~~ C2 9.353 0.093
317 N1 ~~ N7 8.717 0.116
93 n =~ C4 8.496 0.070
293 C11 ~~ N6 8.356 -0.092
208 C6 ~~ C8 8.034 -0.068
115 C1 ~~ N3 7.928 0.088
330 N2 ~~ N10 7.860 -0.077
260 C9 ~~ C12 7.677 -0.098
237 C7 ~~ N8 7.565 0.069
373 N9 ~~ N11 7.562 0.076
137 C2 ~~ N3 7.337 -0.091
323 N2 ~~ N3 7.212 -0.086
148 C3 ~~ C5 6.966 0.078
334 N3 ~~ N5 6.672 0.084
234 C7 ~~ N5 6.580 0.061
139 C2 ~~ N5 6.566 -0.077
94 n =~ C5 6.497 -0.084
118 C1 ~~ N6 6.428 -0.076
174 C4 ~~ C11 6.330 -0.051
223 C6 ~~ N11 6.212 -0.077
283 C10 ~~ N9 6.183 -0.052
341 N3 ~~ N12 6.151 -0.094
372 N9 ~~ N10 6.034 -0.068
374 N9 ~~ N12 6.020 0.083
244 C8 ~~ C11 5.827 -0.051
191 C5 ~~ C9 5.783 -0.070
307 C12 ~~ N8 5.622 0.080
226 C7 ~~ C9 5.466 -0.063
241 C7 ~~ N12 5.409 0.066
310 C12 ~~ N11 5.382 -0.069
82 c =~ N5 5.247 0.085
348 N4 ~~ N11 5.174 -0.065
91 n =~ C2 5.132 -0.087
315 N1 ~~ N5 5.094 0.078
295 C11 ~~ N8 5.055 -0.070
335 N3 ~~ N6 4.991 -0.079
194 C5 ~~ C12 4.900 0.066
203 C5 ~~ N9 4.841 -0.057
368 N8 ~~ N9 4.834 -0.066
277 C10 ~~ N3 4.738 -0.051
199 C5 ~~ N5 4.588 0.055
192 C5 ~~ C10 4.568 -0.043
274 C10 ~~ C12 4.568 0.052
319 N1 ~~ N9 4.513 0.073
157 C3 ~~ N2 4.475 -0.066
300 C12 ~~ N1 4.436 0.082
331 N2 ~~ N11 4.383 0.057
196 C5 ~~ N2 4.023 -0.052
377 N11 ~~ N12 4.016 0.064
352 N5 ~~ N8 4.009 0.060# Korrelation der Summenwerte mit Minderungskorrektur (-> Explizite Prüfung der Annahme unkorrelierter Faktoren)
cor(neo$C_sum, neo$N_sum)[1] -0.4071619cor(neo$C_sum, neo$N_sum) / sqrt(alpha_gewiss$est * alpha_neuro$est)[1] -0.4678935# CFA für modifiziertes Modell mit korrelierten Faktoren
model_corr <- "
c =~ C1 + C2 + C3 + C4 + C5 + C6 + C7 + C8 + C9 + C10 + C11 + C12
n =~ N1 + N2 + N3 + N4 + N5 + N6 + N7 + N8 + N9 + N10 + N11 + N12
c ~~ n
"
fit_cfa_C_N_corr <- cfa(model = model_corr, data = neo, std.lv = TRUE, meanstructure = TRUE, estimator = "ML")
summary(fit_cfa_C_N_corr, standardized=TRUE, fit.measures=TRUE)lavaan 0.6.17 ended normally after 21 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 73
Number of observations 566
Model Test User Model:
Test statistic 1080.036
Degrees of freedom 251
P-value (Chi-square) 0.000
Model Test Baseline Model:
Test statistic 5547.954
Degrees of freedom 276
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.843
Tucker-Lewis Index (TLI) 0.827
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -17190.867
Loglikelihood unrestricted model (H1) -16650.849
Akaike (AIC) 34527.735
Bayesian (BIC) 34844.452
Sample-size adjusted Bayesian (SABIC) 34612.712
Root Mean Square Error of Approximation:
RMSEA 0.076
90 Percent confidence interval - lower 0.072
90 Percent confidence interval - upper 0.081
P-value H_0: RMSEA <= 0.050 0.000
P-value H_0: RMSEA >= 0.080 0.105
Standardized Root Mean Square Residual:
SRMR 0.073
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
c =~
C1 0.506 0.039 12.982 0.000 0.506 0.537
C2 0.710 0.043 16.523 0.000 0.710 0.654
C3 0.489 0.043 11.426 0.000 0.489 0.481
C4 0.329 0.026 12.549 0.000 0.329 0.522
C5 0.622 0.037 16.691 0.000 0.622 0.659
C6 0.735 0.047 15.589 0.000 0.735 0.625
C7 0.521 0.034 15.248 0.000 0.521 0.614
C8 0.332 0.027 12.122 0.000 0.332 0.507
C9 0.637 0.043 14.682 0.000 0.637 0.595
C10 0.556 0.031 17.968 0.000 0.556 0.697
C11 0.665 0.042 16.009 0.000 0.665 0.638
C12 0.384 0.043 8.878 0.000 0.384 0.384
n =~
N1 0.208 0.044 4.694 0.000 0.208 0.204
N2 0.674 0.040 16.813 0.000 0.674 0.651
N3 0.873 0.047 18.673 0.000 0.873 0.705
N4 0.739 0.043 17.264 0.000 0.739 0.665
N5 0.756 0.042 18.188 0.000 0.756 0.691
N6 0.985 0.047 21.035 0.000 0.985 0.768
N7 0.631 0.044 14.203 0.000 0.631 0.569
N8 0.622 0.042 14.899 0.000 0.622 0.591
N9 0.818 0.042 19.666 0.000 0.818 0.732
N10 0.781 0.040 19.381 0.000 0.781 0.724
N11 0.948 0.042 22.770 0.000 0.948 0.810
N12 0.482 0.045 10.775 0.000 0.482 0.448
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
c ~~
n -0.493 0.037 -13.290 0.000 -0.493 -0.493
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.C1 2.650 0.040 67.033 0.000 2.650 2.818
.C2 2.495 0.046 54.653 0.000 2.495 2.297
.C3 2.611 0.043 61.135 0.000 2.611 2.570
.C4 3.352 0.027 126.457 0.000 3.352 5.315
.C5 2.459 0.040 61.970 0.000 2.459 2.605
.C6 1.989 0.049 40.216 0.000 1.989 1.690
.C7 2.726 0.036 76.338 0.000 2.726 3.209
.C8 3.408 0.028 123.816 0.000 3.408 5.204
.C9 2.555 0.045 56.813 0.000 2.555 2.388
.C10 2.834 0.034 84.493 0.000 2.834 3.551
.C11 2.797 0.044 63.800 0.000 2.797 2.682
.C12 2.558 0.042 60.779 0.000 2.558 2.555
.N1 1.910 0.043 44.640 0.000 1.910 1.876
.N2 1.647 0.044 37.818 0.000 1.647 1.590
.N3 1.903 0.052 36.563 0.000 1.903 1.537
.N4 1.993 0.047 42.635 0.000 1.993 1.792
.N5 1.920 0.046 41.764 0.000 1.920 1.755
.N6 1.776 0.054 32.911 0.000 1.776 1.383
.N7 2.037 0.047 43.635 0.000 2.037 1.834
.N8 2.041 0.044 46.161 0.000 2.041 1.940
.N9 1.581 0.047 33.689 0.000 1.581 1.416
.N10 2.069 0.045 45.640 0.000 2.069 1.918
.N11 1.790 0.049 36.365 0.000 1.790 1.529
.N12 2.481 0.045 54.847 0.000 2.481 2.305
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.C1 0.629 0.040 15.819 0.000 0.629 0.711
.C2 0.675 0.045 14.971 0.000 0.675 0.572
.C3 0.793 0.049 16.078 0.000 0.793 0.768
.C4 0.289 0.018 15.896 0.000 0.289 0.727
.C5 0.504 0.034 14.919 0.000 0.504 0.566
.C6 0.844 0.055 15.238 0.000 0.844 0.610
.C7 0.450 0.029 15.326 0.000 0.450 0.623
.C8 0.319 0.020 15.969 0.000 0.319 0.743
.C9 0.739 0.048 15.464 0.000 0.739 0.646
.C10 0.327 0.023 14.477 0.000 0.327 0.514
.C11 0.645 0.043 15.122 0.000 0.645 0.593
.C12 0.855 0.052 16.397 0.000 0.855 0.853
.N1 0.993 0.059 16.754 0.000 0.993 0.958
.N2 0.618 0.039 15.651 0.000 0.618 0.576
.N3 0.771 0.051 15.247 0.000 0.771 0.503
.N4 0.691 0.044 15.563 0.000 0.691 0.558
.N5 0.625 0.041 15.363 0.000 0.625 0.522
.N6 0.676 0.047 14.528 0.000 0.676 0.411
.N7 0.835 0.052 16.063 0.000 0.835 0.677
.N8 0.719 0.045 15.967 0.000 0.719 0.650
.N9 0.579 0.039 14.979 0.000 0.579 0.464
.N10 0.553 0.037 15.060 0.000 0.553 0.475
.N11 0.471 0.034 13.769 0.000 0.471 0.344
.N12 0.926 0.056 16.424 0.000 0.926 0.799
c 1.000 1.000 1.000
n 1.000 1.000 1.000# Prüfung des lokalen Fit im modifizierten Modell
mod_ind <- modindices(fit_cfa_C_N_corr, sort.=TRUE, standardized = FALSE)
subset(mod_ind[order(mod_ind$mi, decreasing=TRUE), ], mi > 4) lhs op rhs mi epc
347 N4 ~~ N10 96.545 0.285
86 c =~ N9 58.034 -0.331
100 n =~ C11 51.840 -0.322
189 C5 ~~ C7 49.837 0.160
229 C7 ~~ C12 47.198 0.191
242 C8 ~~ C9 41.780 0.142
171 C4 ~~ C8 36.154 0.081
101 n =~ C12 33.768 0.286
128 C2 ~~ C6 32.733 0.206
227 C7 ~~ C10 25.797 0.095
287 C11 ~~ C12 25.684 -0.170
129 C2 ~~ C7 24.165 -0.129
228 C7 ~~ C11 24.050 -0.125
175 C4 ~~ C12 23.848 0.107
111 C1 ~~ C11 21.824 0.138
85 c =~ N8 21.185 0.215
173 C4 ~~ C10 20.395 0.066
304 C12 ~~ N5 18.725 0.140
93 n =~ C4 18.317 0.125
375 N10 ~~ N11 17.900 -0.110
238 C7 ~~ N9 17.352 -0.098
326 N2 ~~ N6 17.080 0.128
126 C2 ~~ C4 16.568 -0.083
190 C5 ~~ C8 15.450 -0.073
107 C1 ~~ C7 15.339 -0.096
134 C2 ~~ C12 13.131 -0.125
82 c =~ N5 13.017 0.161
346 N4 ~~ N9 12.577 -0.105
316 N1 ~~ N6 12.268 -0.130
324 N2 ~~ N4 12.025 -0.104
95 n =~ C6 11.858 -0.176
90 n =~ C1 11.756 0.148
88 c =~ N11 10.974 -0.136
169 C4 ~~ C6 10.498 -0.073
153 C3 ~~ C10 10.126 -0.076
133 C2 ~~ C11 9.532 0.098
102 C1 ~~ C2 9.307 0.092
212 C6 ~~ C12 9.230 -0.116
237 C7 ~~ N8 9.222 0.077
317 N1 ~~ N7 9.084 0.118
340 N3 ~~ N11 9.042 0.092
293 C11 ~~ N6 8.865 -0.092
132 C2 ~~ C10 8.790 -0.069
231 C7 ~~ N2 8.776 -0.071
115 C1 ~~ N3 8.595 0.092
274 C10 ~~ C12 8.574 0.072
357 N6 ~~ N7 8.397 -0.102
208 C6 ~~ C8 8.296 -0.068
234 C7 ~~ N5 8.136 0.069
372 N9 ~~ N10 8.000 -0.077
323 N2 ~~ N3 7.814 -0.089
334 N3 ~~ N5 7.667 0.090
244 C8 ~~ C11 7.526 -0.057
194 C5 ~~ C12 7.489 0.082
307 C12 ~~ N8 7.361 0.093
154 C3 ~~ C11 7.219 0.088
283 C10 ~~ N9 7.166 -0.055
330 N2 ~~ N10 7.153 -0.073
137 C2 ~~ N3 6.927 -0.088
81 c =~ N4 6.879 0.122
174 C4 ~~ C11 6.875 -0.052
341 N3 ~~ N12 6.672 -0.098
99 n =~ C10 6.406 0.083
191 C5 ~~ C9 6.400 -0.073
273 C10 ~~ C11 6.393 -0.057
92 n =~ C3 6.199 -0.119
223 C6 ~~ N11 6.091 -0.075
352 N5 ~~ N8 5.833 0.074
199 C5 ~~ N5 5.712 0.062
241 C7 ~~ N12 5.680 0.068
315 N1 ~~ N5 5.533 0.082
139 C2 ~~ N5 5.517 -0.070
295 C11 ~~ N8 5.442 -0.072
243 C8 ~~ C10 5.352 0.035
148 C3 ~~ C5 5.344 0.067
282 C10 ~~ N8 5.313 0.051
368 N8 ~~ N9 5.306 -0.069
203 C5 ~~ N9 5.271 -0.058
118 C1 ~~ N6 5.206 -0.069
260 C9 ~~ C12 4.968 -0.079
348 N4 ~~ N11 4.957 -0.063
310 C12 ~~ N11 4.835 -0.065
300 C12 ~~ N1 4.832 0.086
170 C4 ~~ C7 4.813 0.036
335 N3 ~~ N6 4.726 -0.077
374 N9 ~~ N12 4.666 0.072
319 N1 ~~ N9 4.631 0.073
226 C7 ~~ C9 4.408 -0.056
157 C3 ~~ N2 4.357 -0.065
87 c =~ N10 4.179 0.087# Prüfung des globalen Fit via Dimensionalität
fa.parallel(neo[, c(gewiss_items, neuro_items)],
fm = "ml",
fa = "fa",
quant = 0.95,
n.iter = 1000)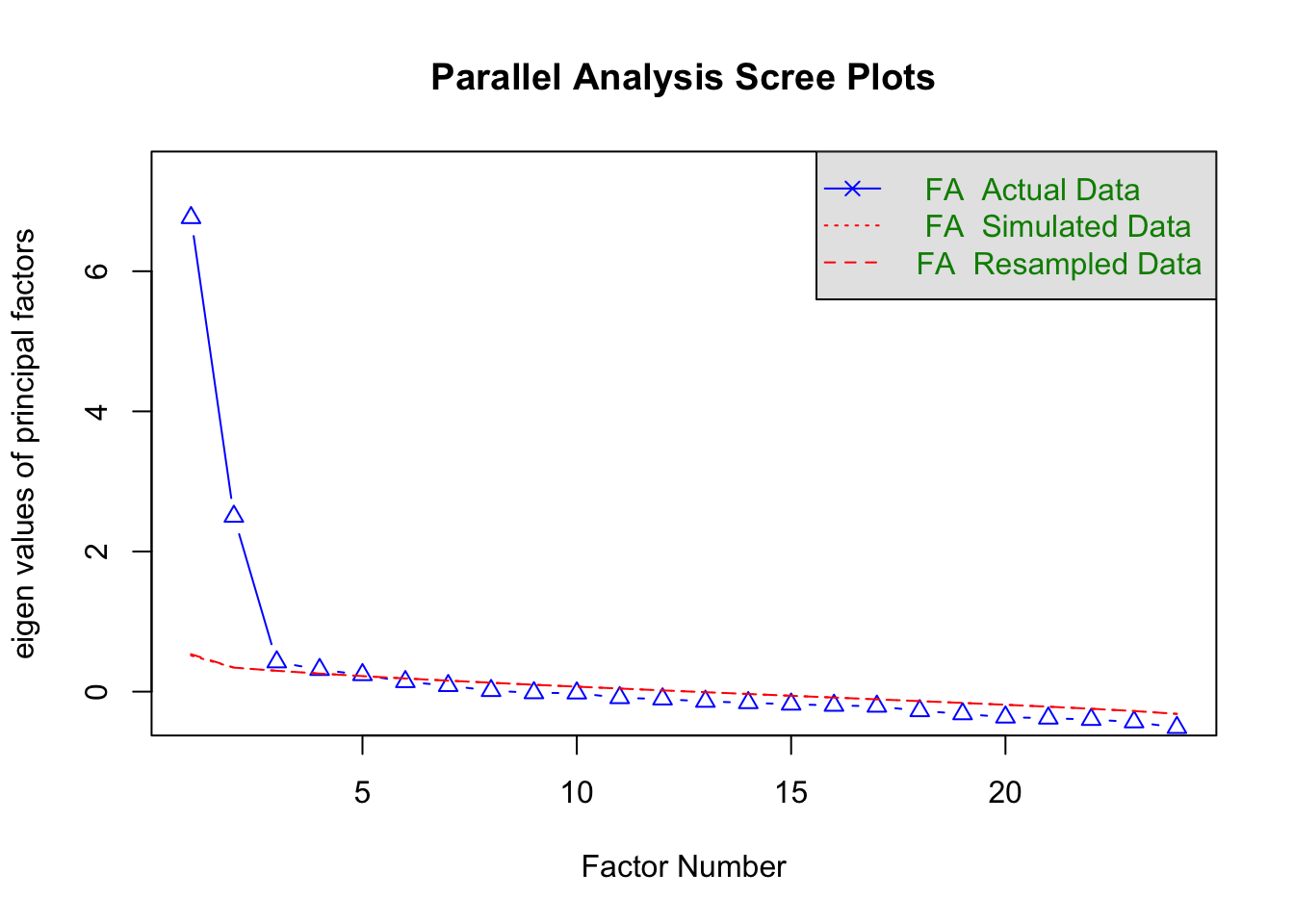
Parallel analysis suggests that the number of factors = 4 and the number of components = NA ## Kriteriumsvalidität
# CFA mit Gewissenhaftigkeit und dem Kriterium Alter
model_age <- "
c =~ C1 + C2 + C3 + C4 + C5 + C6 + C7 + C8 + C9 + C10 + C11 + C12
c ~~ Age
"
fit_cfa_C_Age <- cfa(model = model_age, data = neo, std.lv = TRUE, meanstructure = TRUE, estimator = "ML")
summary(fit_cfa_C_Age, standardized=TRUE, fit.measures=TRUE)lavaan 0.6.17 ended normally after 27 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 39
Number of observations 566
Model Test User Model:
Test statistic 482.838
Degrees of freedom 65
P-value (Chi-square) 0.000
Model Test Baseline Model:
Test statistic 2231.108
Degrees of freedom 78
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.806
Tucker-Lewis Index (TLI) 0.767
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -10331.729
Loglikelihood unrestricted model (H1) -10090.310
Akaike (AIC) 20741.458
Bayesian (BIC) 20910.663
Sample-size adjusted Bayesian (SABIC) 20786.856
Root Mean Square Error of Approximation:
RMSEA 0.107
90 Percent confidence interval - lower 0.098
90 Percent confidence interval - upper 0.116
P-value H_0: RMSEA <= 0.050 0.000
P-value H_0: RMSEA >= 0.080 1.000
Standardized Root Mean Square Residual:
SRMR 0.066
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
c =~
C1 0.513 0.039 13.179 0.000 0.513 0.546
C2 0.702 0.043 16.243 0.000 0.702 0.647
C3 0.478 0.043 11.105 0.000 0.478 0.471
C4 0.340 0.026 13.011 0.000 0.340 0.540
C5 0.618 0.037 16.476 0.000 0.618 0.654
C6 0.722 0.048 15.196 0.000 0.722 0.614
C7 0.527 0.034 15.400 0.000 0.527 0.620
C8 0.339 0.027 12.378 0.000 0.339 0.517
C9 0.637 0.044 14.635 0.000 0.637 0.595
C10 0.566 0.031 18.315 0.000 0.566 0.709
C11 0.638 0.042 15.149 0.000 0.638 0.612
C12 0.407 0.043 9.441 0.000 0.407 0.407
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
c ~~
Age 0.800 0.483 1.658 0.097 0.800 0.075
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.C1 2.650 0.040 67.033 0.000 2.650 2.818
.C2 2.495 0.046 54.653 0.000 2.495 2.297
.C3 2.611 0.043 61.135 0.000 2.611 2.570
.C4 3.352 0.027 126.457 0.000 3.352 5.315
.C5 2.459 0.040 61.970 0.000 2.459 2.605
.C6 1.989 0.049 40.216 0.000 1.989 1.690
.C7 2.726 0.036 76.338 0.000 2.726 3.209
.C8 3.408 0.028 123.816 0.000 3.408 5.204
.C9 2.555 0.045 56.813 0.000 2.555 2.388
.C10 2.834 0.034 84.493 0.000 2.834 3.551
.C11 2.797 0.044 63.800 0.000 2.797 2.682
.C12 2.558 0.042 60.779 0.000 2.558 2.555
Age 30.723 0.450 68.208 0.000 30.723 2.867
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.C1 0.621 0.039 15.728 0.000 0.621 0.702
.C2 0.686 0.046 14.962 0.000 0.686 0.582
.C3 0.804 0.050 16.089 0.000 0.804 0.778
.C4 0.282 0.018 15.762 0.000 0.282 0.709
.C5 0.510 0.034 14.888 0.000 0.510 0.572
.C6 0.864 0.057 15.262 0.000 0.864 0.624
.C7 0.444 0.029 15.207 0.000 0.444 0.615
.C8 0.314 0.020 15.880 0.000 0.314 0.732
.C9 0.739 0.048 15.405 0.000 0.739 0.646
.C10 0.317 0.022 14.207 0.000 0.317 0.498
.C11 0.680 0.045 15.275 0.000 0.680 0.625
.C12 0.837 0.051 16.312 0.000 0.837 0.834
Age 114.833 6.826 16.823 0.000 114.833 1.000
c 1.000 1.000 1.000# Grafische Veranschaulichung des Modells
semPlot::semPaths(fit_cfa_C_Age, whatLabels = "std", intercepts = FALSE, style = "lisrel", layout = "tree")